Volumes of Solids of Revolution Approximating Volumes as
- Slides: 15
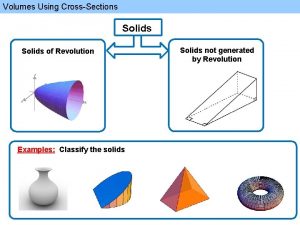
Volumes of Solids of Revolution Approximating Volumes as Integrals of Areas of Slices Examples General Solids of Revolution Other Types of Solids Index FAQ
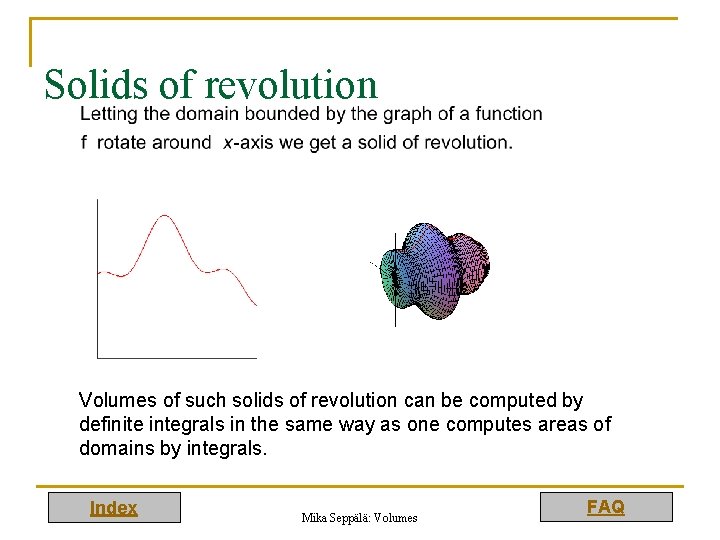
Solids of revolution Volumes of such solids of revolution can be computed by definite integrals in the same way as one computes areas of domains by integrals. Index Mika Seppälä: Volumes FAQ
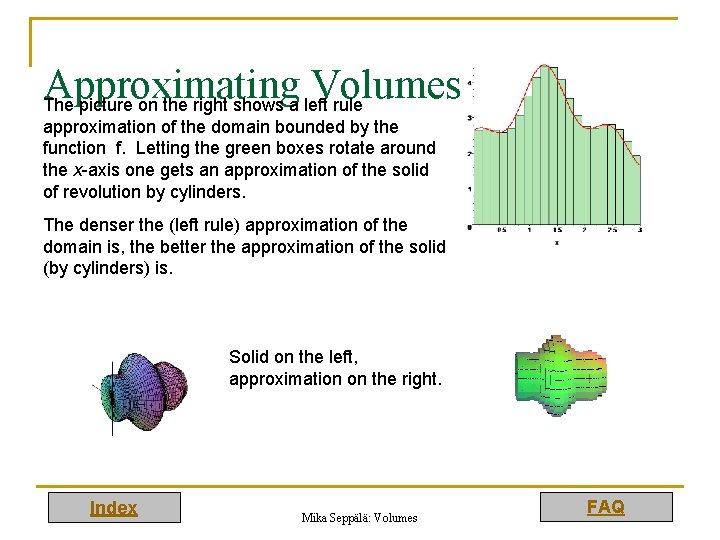
Approximating Volumes The picture on the right shows a left rule approximation of the domain bounded by the function f. Letting the green boxes rotate around the x-axis one gets an approximation of the solid of revolution by cylinders. The denser the (left rule) approximation of the domain is, the better the approximation of the solid (by cylinders) is. Solid on the left, approximation on the right. Index Mika Seppälä: Volumes FAQ
Riemann Sums for Volumes Definition Index Mika Seppälä: Volumes FAQ
Volumes as Integrals of Areas of Slices The slice is obtained by slicing the solid by a plane perpendicular to the x-axis and intersecting the axis at the point x. The slice is a disk of radius f(x). In the picture on the right, the red curve is the graph of the function f, x-axis is tilted down and y-axis is tilted to the right. Index Mika Seppälä: Volumes FAQ
Volume of a Ball Example Index Mika Seppälä: Volumes FAQ
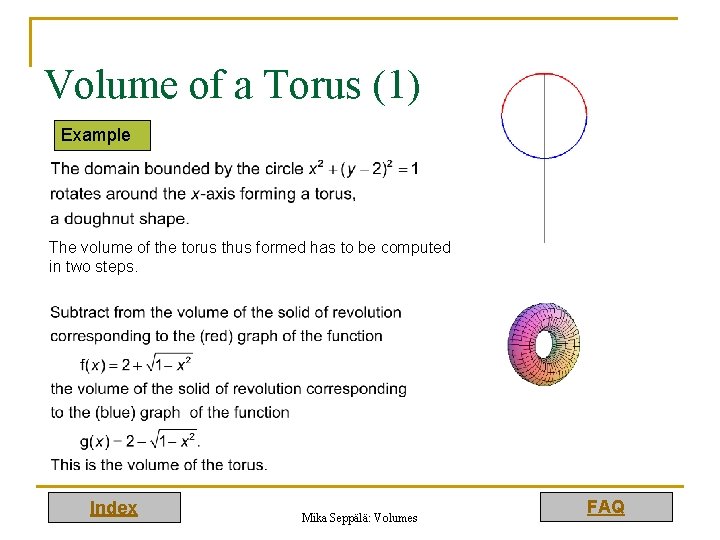
Volume of a Torus (1) Example The volume of the torus thus formed has to be computed in two steps. Index Mika Seppälä: Volumes FAQ
Volume of a Torus (2) Index Mika Seppälä: Volumes FAQ
Volume of a Torus (3) Index Mika Seppälä: Volumes FAQ
Volume of a Torus (4) Shortcut -1 Index Mika Seppälä: Volumes 1 FAQ
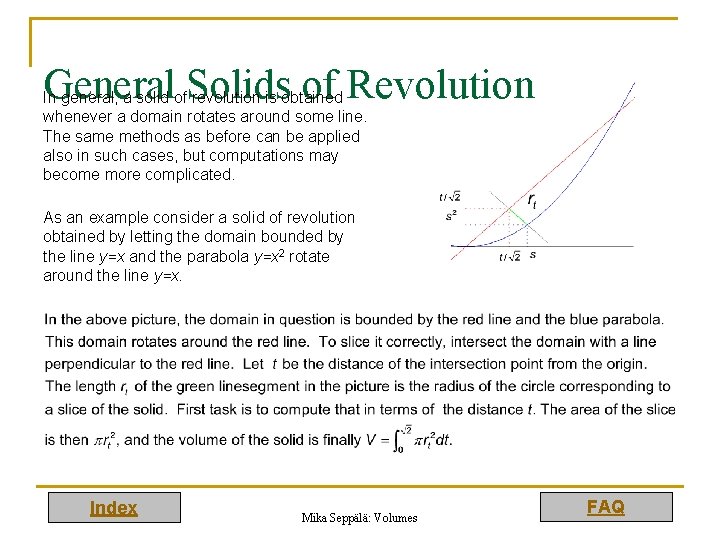
General Solids of Revolution In general, a solid of revolution is obtained whenever a domain rotates around some line. The same methods as before can be applied also in such cases, but computations may become more complicated. As an example consider a solid of revolution obtained by letting the domain bounded by the line y=x and the parabola y=x 2 rotate around the line y=x. Index Mika Seppälä: Volumes FAQ
General Solids of Revolution (2) Index Mika Seppälä: Volumes FAQ
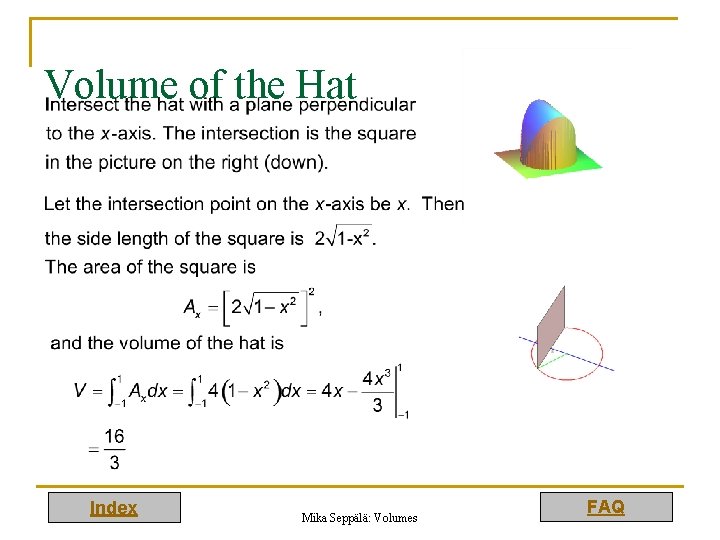
Other Types of Solids Volumes of other types of solids can also be computed by integration. The idea is to perform the following: 1. Slice the solids vertically along some straight line going through the solid. 2. Express the area of the slice as a function of the intersection point of the line and the slice. 3. Integrate this area function to find the volume of the solid. An example of this type of solid is the “hat” above. It is a solid whose bottom face is a disk with radius 1 and center at the origin, and whose every cross section perpendicular to the x-axis is a square. The volume of this solid can be computed by suitable slicing of the solid. Index Mika Seppälä: Volumes FAQ
Volume of the Hat Index Mika Seppälä: Volumes FAQ
Index Mika Seppälä: Volumes FAQ
Volumes of solids with known cross sections
Volumes of solids with known cross sections calculator
Volume of solid with known cross section
A watermelon has an ellipsoidal shape with major axis
Semicircle cross section formula
Cone volume ratio
Estimating square roots
Approximating calculations
Antiderivative
Russian revolution vs french revolution
You should hope this game will be over soon
The third agricultural revolution
Hein
Section 14-3 human molecular genetics answers
Law of combining volumes
11-3 volume of pyramids and cones
