Elementi di Statistica descrittiva Lez 2 Misure di

Elementi di Statistica descrittiva Lez. 2 - Misure di tendenza centrale - le Medie - la Moda - la Mediana __________ Anno scolastico 2001/2002 Prof. Biasco 1

Valori MEDI (o indici di posizione) Nello studio dei fenomeni collettivi è importante calcolare dei valori sintetici che siano rappresentativi dell’insieme dei dati, che diano una visione d’insieme del fenomeno. Tali valori si dicono MEDIE Si possono definire diversi tipi di medie, tra le più comuni si hanno: la media aritmetica, la mediana, la moda, la media geometrica, la media armonica, la media quadratica. 2

Esempio Si vogliono confrontare le stature di 3 gruppi: • Un gruppo di bambini • Un gruppo di giocatori di pallacanestro • Un gruppo di clienti di un supermercato 3

Poligoni di frequenza dei tre gruppi 4

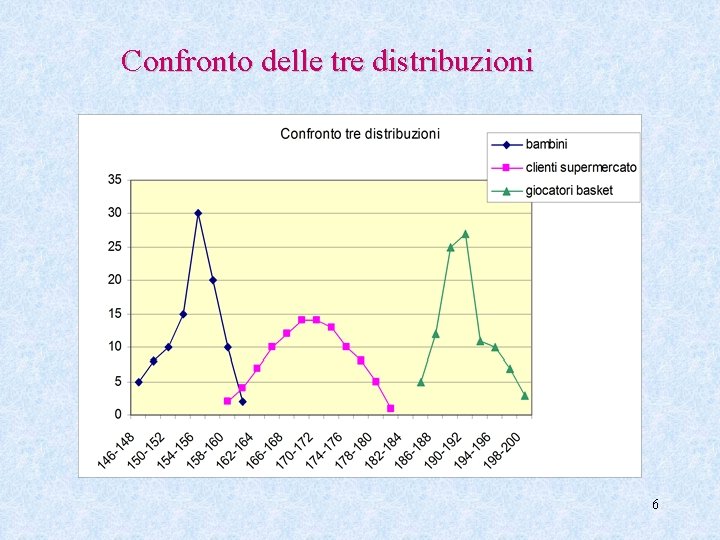
Elementi per cui le tre distribuzioni differiscono • Valore attorno al quale si distribuiscono i dati • Diversa distribuzione dei dati attorno al centro • Presenza più o meno accentuata di code a destra o sinistra • Distribuzione più o meno appuntita. 5

Confronto delle tre distribuzioni 6

Le misure che permettono di valutare sinteticamente tali caratteristiche sono: • Misure di tendenza centrale: MEDIE • Misure di variabilità o dispersione • Misure di forma (asimmetria, curtosi) • Misure di concentrazione. 7

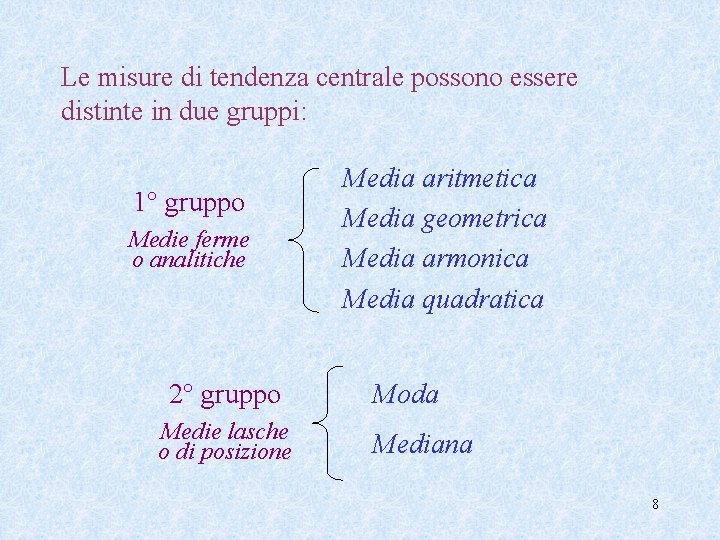
Le misure di tendenza centrale possono essere distinte in due gruppi: 1° gruppo Medie ferme o analitiche 2° gruppo Medie lasche o di posizione Media aritmetica Media geometrica Media armonica Media quadratica Moda Mediana 8

Quali di queste è la Media “più giusta”? Non esiste la “media migliore”, ma la media da utilizzare deve essere scelta in relazione al problema che si sta risolvendo. La media più adatta, “più giusta”, va scelta a seconda dei DATI e degli SCOPI dell’elaborazione statistica. 9

Noi vedremo le seguenti medie: $ La Media aritmetica (semplicemente Media) $ La Media geometrica $ La Media Armonica $ La Media quadratica $ La Moda $ La Mediana 10

Partiamo da un esempio: Esempio 1 Una società di ricerca statistica deve determinare la ricchezza degli abitanti di alcuni paesi al fine di decidere dove aprire alcuni punti vendita per una ditta operante nel settore commerciale. I dati raccolti sono riportati nella seguente tabella 11

Esempio 1 - Tabella. dei redditi rilevati 12

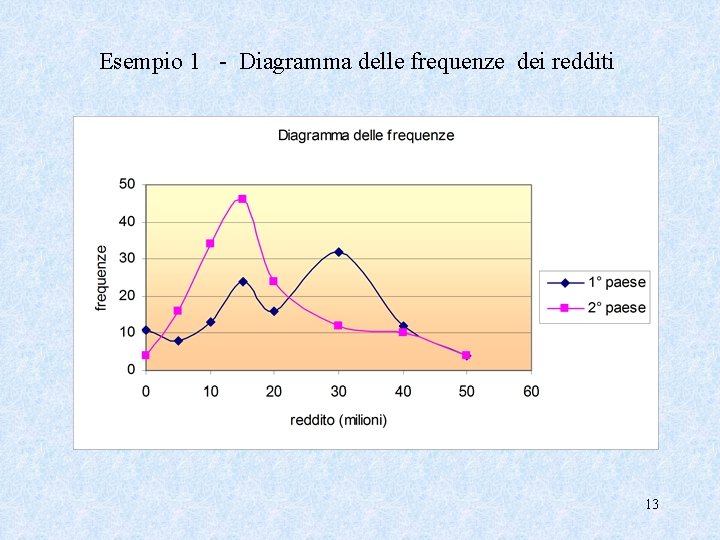
Esempio 1 - Diagramma delle frequenze dei redditi 13

Vogliamo calcolare dei valori numerici che siano indicativi del grado di ricchezza/povertà della popolazione del paese considerato. Gli indici più utili potrebbero essere: – il reddito medio – il reddito più diffuso – il reddito rispetto al quale la popolazione risulta divisa in due parti uguali. 14

La Media Aritmetica La media aritmetica rappresenta il reddito che ogni abitante avrebbe se il reddito totale del paese venisse equamente suddiviso tra tutti gli abitanti cioè nel caso in cui 1 - ciascun abitante versa al sindaco tutto il suo reddito (reddito totale non cambia), 2 - Il sindaco divide in parti uguali il reddito totale della città e lo ridistribuisce ai singoli cittadini. 15

Vediamo come calcolarlo. Se x 1, x 2, … xn sono i redditi degli n abitanti il Reddito medio (la MEDIA dei redditi) viene calcolata nel modo seguente: 1. Calcoliamo il reddito totale della popolazione: 16

2. Dividiamolo per il numero degli abitanti Quindi la media dei redditi è: 17

Tornando all’esempio 1 Reddito relativo al 1° paese. 18

In generale, se x 1, x 2, … xn sono n dati numerici, la loro Media aritmetica (media aritmetica semplice) si ottiene sommando tutti i dati numerici e dividendo la somma per il numero dei dati: 19

Dalla formula precedente avremo: 20

In particolare se gli n dati numerici sono tali che: il dato x 1 compare f 1 volte, x 2 f 2 volte, …. xk fk volte, la Media Aritmetica (Media aritmetica ponderata) è data da: 21

Proprietà della media aritmetica 1. La media aritmetica è sempre compresa tra il valore minimo e il valore massimo x min media xmax 2. La somma degli scarti dalla media è sempre zero posto xi = xi – media = xi – M (scarto dalla media) si ha che: 22

3. La somma dei quadrati degli scarti dalla media è minore della somma dei quadrati degli scarti da qualsiasi altro valore numerico Cioè se M è la media e A un qualsiasi altro numero allora 23

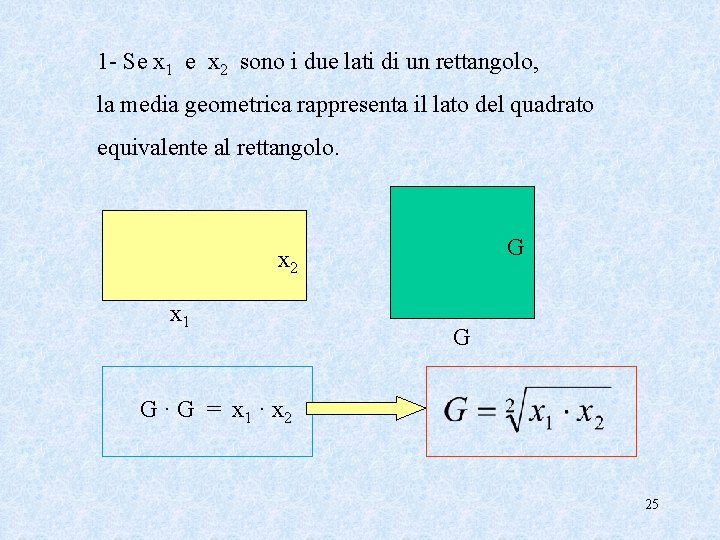
La Media Geometrica Def. Siano x 1, x 2, … xn gli n valori, tutti >0, assunti da una variabile numerica La media geometrica G di questi valori è: Vediamo qualche esempio: 1 - Se x 1 e x 2 sono i due lati di un rettangolo, la media geometrica rappresenta il lato del quadrato equivalente al rettangolo. 24

1 - Se x 1 e x 2 sono i due lati di un rettangolo, la media geometrica rappresenta il lato del quadrato equivalente al rettangolo. G x 2 x 1 G G · G = x 1 · x 2 25

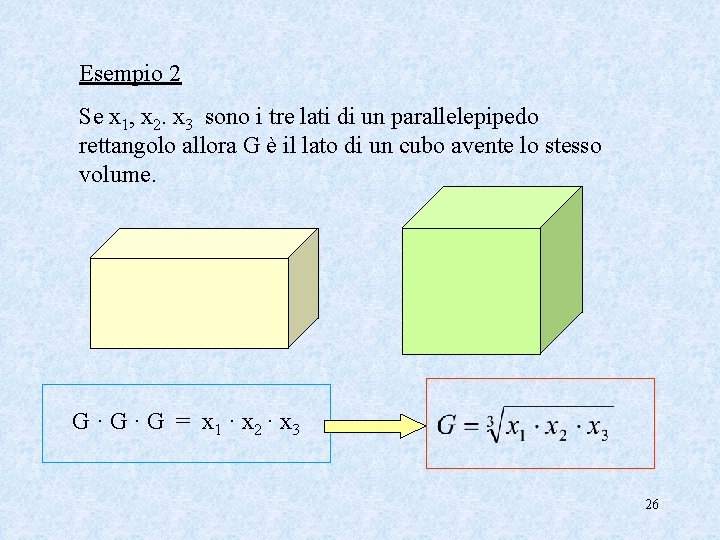
Esempio 2 Se x 1, x 2. x 3 sono i tre lati di un parallelepipedo rettangolo allora G è il lato di un cubo avente lo stesso volume. G · G = x 1 · x 2 · x 3 26

• se gli n dati numerici positivi sono tali che: il dato x 1 compare f 1 volte, x 2 f 2 volte, …. xk fk volte, la Media Geometrica è data da: 27

Esempio 3 Un capitale iniziale di 5. 000 euro viene investito ad interesse composto. Sapendo che il tasso d’interesse il primo anno è del 2%, del 4% il secondo anno e del 6% il terzo anno, calcolare il tasso medio relativo ai tre anni. C 0 = 5000 capitale iniziale: C 1 = C 0 + C 0 *r 1 = C 0(1 + r 1) = 5000(1 + r 1) capitale alla fine del 1°anno C 2 = C 1 + C 1*r 2 = C 1(1 + r 2) = C 0(1 + r 1)(1 + r 2) capitale alla fine del 2° anno C 3 = C 2 + C 2*r 3 = C 2(1 + r 3) = C 0(1 + r 1)(1 + r 2) (1 + r 3) capitale alla fine del 3° anno 28

se indichiamo con r il tasso medio annuo costante deve risultare: C 3 = C 0(1 + r)3 Per cui da C 3 = C 0(1 + r 1)(1 + r 2) (1 + r 3)= C 0(1 + r)3 avremo che (1+r) è la media geometrica (1 + r) = 3 (1 + r 1)(1 + r 2) (1 + r 3) quindi (1 + r)3 = 5622, 24/5000 1 + r = 3 1, 124 da cui r 3, 9 % diversa dalla media aritmetica dei tassi = 4% 29

Esempio 4 Il numero di microrganismi di una certa coltura è aumentato da 2000 a 9000 in 3 giorni. Calcolare l’incremento medio giornaliero. n 0 = 2000 numero iniziale batteri: n 1 = n 0 + n 0 *r = n 0(1 + r) = 2000(1 + r) batteri alla fine del 1°giorno n 2 = n 1 + n 1*r = n 1(1 + r) = n 0(1 + r)2= 2000(1 + r)2 batteri alla fine del 2° giorno n 3 = n 2 + n 2*r = n 2(1 + r) = n 0(1 + r)3 = 2000(1 + r)3 batteri alla fine del 3° giorno 30

Esempio 4 E poiché alla fine del 3° giorno ci sono 9000 batteri 2000(1 + r)3 = 9000/2000 1 + r = 3 4, 5 r = 65, 1 % 31

La Media Armonica Def. Siano x 1, x 2, … xn gli n valori, tutti >0, assunti da una variabile numerica La media armonica H di questi valori è: 32

La Media Quadratica Def. Siano x 1, x 2, … xn gli n valori assunti da una variabile numerica La media quadratica Q di questi valori è: 33

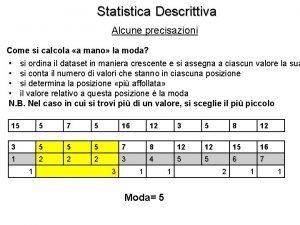
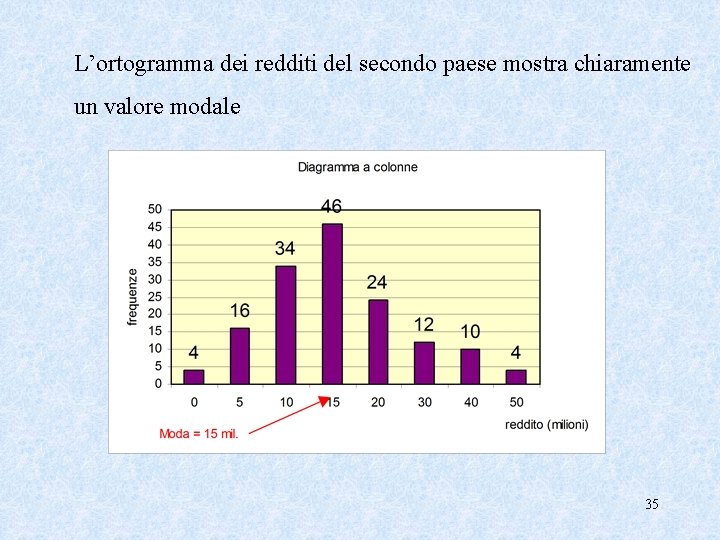
La Moda (o valore modale) La moda è uguale al dato che, nella distribuzione, compare con frequenza più elevata, cioè è il dato più rilevante, il dato più diffuso. Nel caso dell’ Esempio 1 - 2° paese Moda= = 15 milioni infatti 15 milioni è il reddito più diffuso Cioè il gruppo di abitanti con un reddito di 15 mil. è il più numeroso. 34

L’ortogramma dei redditi del secondo paese mostra chiaramente un valore modale 35

Osservazioni La MODA è un valore medio interessante Se la moda è un reddito basso allora c’è un gruppo consistente di cittadini poveri Se la moda è un valore alto c’è un gruppo consistente di cittadini ricchi. Se il reddito è legato al tipo di attività potrebbe indicare che in quel paese una certa attività è la più diffusa, o indicare il ceto sociale prevalente. 36

Esempio: Se in 100 lanci di un dado otteniamo come valore modale “significativo” il numero 5 allora con molta probabilità il dado è truccato. 37

La Mediana è una media di posizione, è uguale al valore che si trova al centro di una distribuzione ordinata in modo crescente (o decrescente) La Mediana divide i dati in due parti tali che : • il numero di osservazioni della Mediana è uguale al • numero di osservazioni della Mediana 38

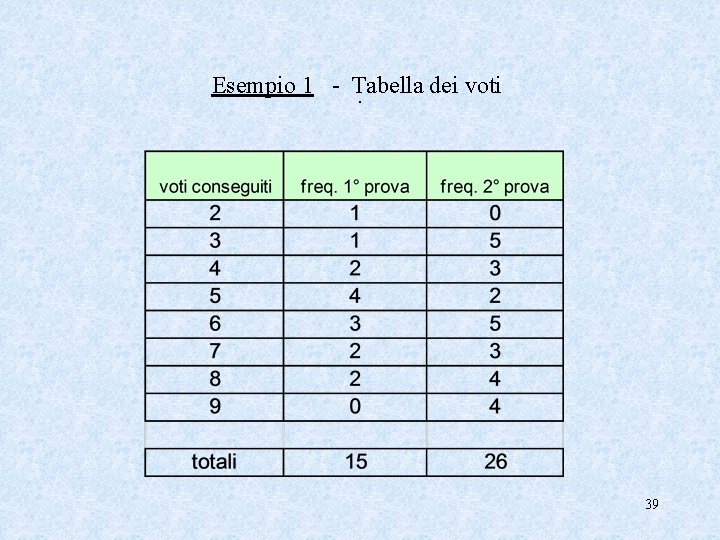
Esempio 1 - Tabella dei voti. 39

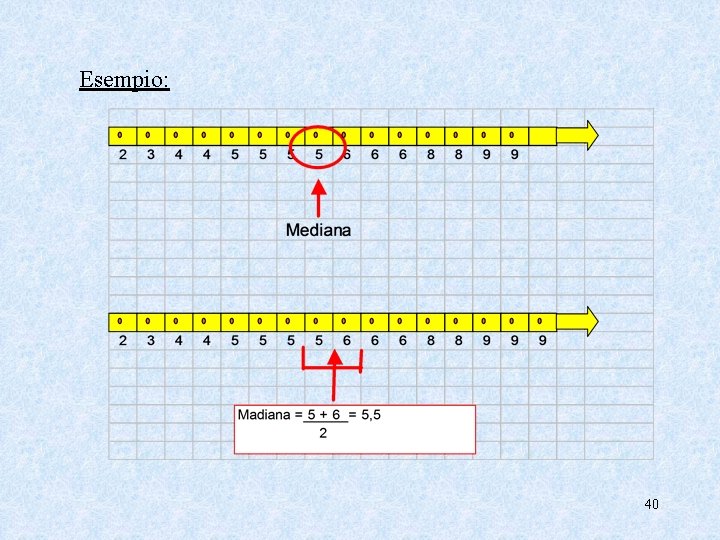
Esempio: 40

Io sono il valore MEDIANO 41

Fine lezione 42