Dott ssa Arianna Orasi 5 Marzo 2010 Contenuto

Dott. ssa Arianna Orasi 5 Marzo 2010

Contenuto del corso • Parte 1: Richiami alla probabilità ed elementi di statistica descrittiva • Parte 2: Analisi statistiche dei dati di onda

Parte 1 • Introduzione alla statistica • Alcuni richiami alla probabilità • Statistica descrittiva(1) Ringrazio Guido Masarotto e Carlo Gaetan per aver messo a disposizione il loro materiale didattico

Introduzione alla statistica Un pò di terminologia…. . • • Unità statistiche Dati Variabili Modalità Campione Dati qualitativi: sconnessi ordinali Dati quantitativi: interi o continui

Un utile strumento: R • http: //www. r-project. org/ • R 2. 10. 1.

Alcuni semplici comandi ls() per controllare cosa c’è nella directory di lavoro chiamata anche workspace rm() per eliminare gli oggetti presenti > (2 + 3) * 4 [1] 20 >4*3**3 #Usa ** o ^ per calcolare un elevamento a potenza R oltre a possedere un gran numero di funzioni dà la possibilità di incrementarne di nuove e questo è uno dei punti di forza di questo programma. Per chiedere aiuto su una funzione o più in generale si digita > help. start()

Alcuni semplici comandi Si può salvare un valore assegnandolo ad un oggetto mediante il simbolo <> x <- sqrt(2) #salva in x la radice quadrata di 2 >x [1] 1. 414214 Molto utile è la possibilità di gestire operazioni e variabili logiche: > x <- 10 #fissa x uguale a 10 > x > 10 # x e' piu' grande di 10? [1] FALSE > x<=10 [1] TRUE Gli operatori logici sono: <, <=, >, >=, ==, !=, &(intersezione), | (unione)

Alcuni semplici comandi Per creare un vettore si usa la funzionie c() >x <- c(2, 3, 5, 7, 11) >x [1] 2 3 5 7 11 Per creare sequenze di numeri si può usare la notazione a: b >xx <- 1: 10 >xx [1] 1 2 3 4 5 6 7 8 9 10 >xx <- 100: 1 >xx [1] ? La stessa operazione poteva essere fatta con il comando seq >xx<-seq(from=100, to=1)

Alcuni richiami alla probabilità VARIABILI CASUALI e DEFINIZIONE DI PROBABILITÀ Una variabile casuale (v. c. ) è il risultato numerico di un esperimento quando questo non è prevedibile con certezza. Ne sappiamo qualcosa…ma non proprio tutto! Come stima della probabilità di un evento sperimentale può essere utilizzata la sua frequenza. La frequenza relativa di un campione all’aumentare del numero delle osservazioni tende a diventare sempre più simile a quella reale della popolazione (legge empirica del caso) e tale concetto costituisce la base sperimentale dela teoria statistica. In questi casi si parla di probabilità frequentista o a posteriori (perchè le leggi dei fenomeni studiati non sono note a priori). Non è la sola definizione di probabilità esistente ma è quella che useremo in seguito.

Richiami alla probabilità CALCOLO COMBINATORIO La stima della probabilità di un evento è uno strumento fondamentale della statistica. Nelle sue forme più semplici si fonda sul calcolo combinatorio. L’associazione del concetto di probabilità al calcolo combinatorio è importante: serve per collegare una scelta alla probabilità con la quale l’evento atteso può avvenire nel contesto di tutti gli event alternativi possibili. È la base dell’inferenza statistica, della scelta scientifica in tutti i casi di incertezza.

Richiami alla probabilità LE PERMUTAZIONI SEMPLICI SENZA RIPETIZIONE Tutti i sottoinsiemi che si possono formare collocando n elementi in tutti gli ordini possibili si chiamano permutazioni. Questo numero si calcola con il fattoriale di un numero n, che indichiamo con n!, cioè il prodotto di un intero positivo n per tutti gli interi positivi più piccoli di questo fino ad 1 ossia: n x (n-1) x (n-2) x (n-3) x…. x 1 si ottiene semplicemente utilizzando: > prod(1: n) o in alternativa la funzione factorial >factorial(n)

Alcuni richiami alla probabilità LE DISPOSIZIONE SEMPLICI SENZA RIPETIZIONE Le disposizioni semplici di n oggetti a gruppi di k, Dn, k, sono il prodotto di un intero positivo n per i primi (k - 1) interi positivi più piccoli di questi, e sappiamo fornisce tutti gruppi che si possono formare prendendo k tra n oggetti distinti, in modo che ogni gruppo differisca dai restanti o per un elemento o per l’ordine con cui gli oggetti sono disposti e si ottiene come o si può scrivere come prod((n-k+1): n). Ad esempio D 6, 3 > prod((6 -3+1): 6) [1] 120

Alcuni richiami alla probabilità LE COMBINAZIONI SEMPLICI SENZA RIPETIZIONE Esercizio Come calcolareste con R le combinazioni di n oggetti a gruppi di k indicate con il simbolo del coefficiente binomiale

Alcuni richiami alla probabilità LE COMBINAZIONI SEMPLICI SENZA RIPETIZIONE Soluzione : -) c’è la funzione choose > choose(4, 2) [1] 6

Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ Le v. c. hanno una propria distribuzione di probabilità che in sostanza è una funzione matematica che per ogni valore della variabile fornisce la probabilità che venga osservato quel valore (caso discreto) o che il risultato cada in un certo intervallo finito di valori (caso continuo). Esistono funzioni di probabilità discrete e continue: Tra quelle discrete: binomiale, multinomiale, poissoniana, geometrica, uniforme Tra quelle continue: normale, esponenziale negativa, gamma, derivanti dalla normale: chi quadro, t di student, F di Fisher

Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ: BINOMIALE In un collettivo con n unità che possono essere ripartite solo in due classi A e B con frequenze relative p=na/n e q=nb/n, la probabilita di avere i volte l’evento A (o n-i volte l’evento B) è data da dove ricordiamo che sono combinazioni semplici. Tale distribuzione mi fornisce la probabilità che un evento con probabilità a priori p avvenga 1, 2, 3, …i volte in n prove ripetute identiche e indipendenti. La media è data da p e la varianza è data da (p*q)/n

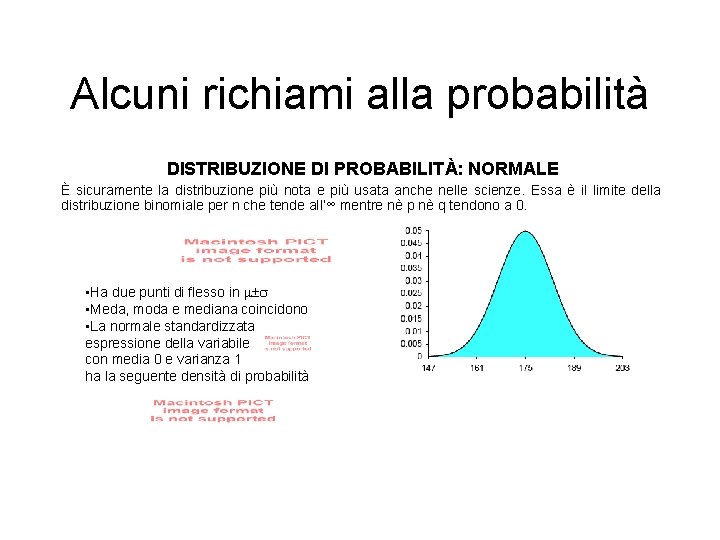
Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ: NORMALE È sicuramente la distribuzione più nota e più usata anche nelle scienze. Essa è il limite della distribuzione binomiale per n che tende all’∞ mentre nè p nè q tendono a 0. • Ha due punti di flesso in • Meda, moda e mediana coincidono • La normale standardizzata espressione della variabile con media 0 e varianza 1 ha la seguente densità di probabilità

Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ R consente di gestire tutte le principali variabili casuali e permette il calcolo della funzione di probabilità o di densità, della funzione di ripartizione, quantili e generazione di numeri casuali

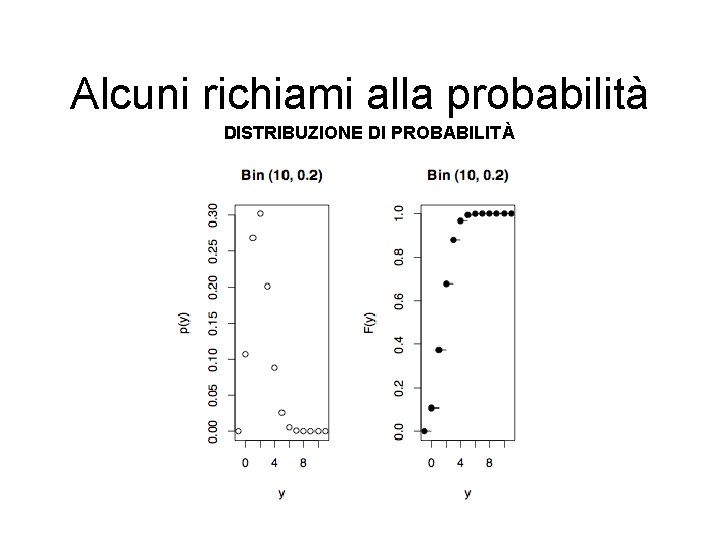
Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ Esempio: Sia X ~ Bin(n=10, p=0. 2) - la probabilità che X assuma valore x=2 è data da: > dbinom(2, 10, 0. 2) [1] 0. 3019899 - la funzione di ripartizione ossia la P(X<=x)=F(x) > pbinom(2, 10, 0. 2) [1] 0. 6777995 - per i quantili della distribuzione ossia il più piccolo valore di x t. c. F(x)>= > qbinom(0. 45, 10, 0. 2) [1] 2

Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ Per rappresentare la distribuzione di probabilità di una v. c. ß(10, 0. 2) e la sua funzione di ripartizione >par (mfrow=c(1, 2)) >y <- seq(-1, 11, by=1) >plot( y, dbinom (y, 10, 0. 2), type="p", ylab="p(y)", main="Bin (10, 0. 2)" ) >plot ( y, pbinom ( y, 10, 0. 2 ), type="p", pch=16, ylab="F(y)", main="Bin (10, 0. 2)" ) >segments ( -1: 10, pbinom ( -1: 10, 0. 2 ), 0: 11, pbinom ( -1: 10, 0. 2 ) )

Alcuni richiami alla probabilità DISTRIBUZIONE DI PROBABILITÀ

Alcuni richiami alla probabilità SIMULAZIONE DI VARIABILI CASUALI Per generare una serie di numeri casuali da una distribuzione, come ad esempio da una distribuzione normale la sintassi è: > x<-rnorm(10) TEOREMI LIMITE LEGGE FORTE DEI GRANDI NUMERI Se Xi i=1, … è una successione di variabili indipendenti e identicamente distribuite con valore atteso E(Xi)= allora la media campionaria converge quasi certamente al valore Per convergenza q. c. di una successione di v. c. Xi i=1, … ad una costante c si intende che la sequenza è t. c.

Alcuni richiami alla probabilità TEOREMI LIMITE LEGGE FORTE DEI GRANDI NUMERI Verifichiamola empiricamente con R Partiamo generando n valori casuali ad esempio da una distribuzionie di Poisson. Sia n=10 replicazioni da X~Poisson(5) e calcoliamo la media aritmetica >set. seed(30) >x<-rpois(10, 5) >mean(x) [1] 4. 5 Raddoppiamo le replicazioni >x<-c(x, rpois(10, 5)) >mean(x) [1] 4. 7 Raddoppiamo ancora >x<-c(x, rpois(20, 5)) >mean(x) [1] 4. 325 la media campionaria sta oscllando intorno al vero valore della media

Alcuni richiami alla probabilità TEOREMI LIMITE LEGGE FORTE DEI GRANDI NUMERI Proviamo con mille replicazioni >x<-c(x, rpois(1000, 5)) >mean(x) [1] 4. 907692 Con 10000 replicazioni >x<-c(x, rpois(10000, 5)) >mean(x) [1] 5. 000181 Evviva! Come volevamo la media campionaria si avvicina al vero valore della media della distribuzione campionaria di riferimento al crescere delle replicazioni

Alcuni richiami alla probabilità TEOREMI LIMITE LEGGE DEBOLE DEI GRANDI NUMERI Se Xi i=1, … è una successione di variabili indipendenti e identicamente distribuite con valore atteso E(Xi)= allora la media campionaria converge in probabilità al valore Per convergenza in probabiliità di una successione di v. c. Xi i=1, … ad una costante c si intende che la sequenza è t. c.

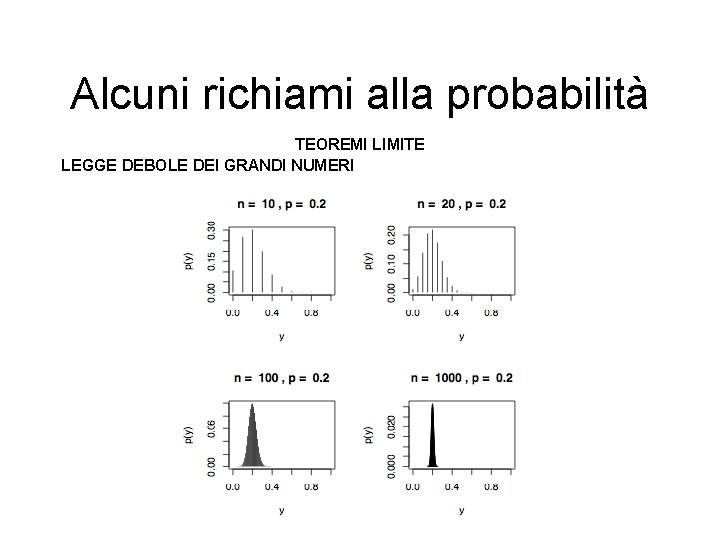
Alcuni richiami alla probabilità TEOREMI LIMITE LEGGE DEBOLE DEI GRANDI NUMERI Verifichiamola ancora empiricamente con R Partiamo generando n valori casuali ad esempio da una distribuzionie Binomiale. Calcoliamo la media aritmetica > n<-10 > p<-0. 2 > nobs<-c(10, 20, 1000) > par(mfrow=c(2, 2)) > for (n in nobs) { x<-0: n d<-dbinom(x, n, p) y<-(x/n) plot(y, d, type='h', main=paste("n = ", n, ", p = ", p), ylab="p(y)", xlab='y')}

Alcuni richiami alla probabilità TEOREMI LIMITE LEGGE DEBOLE DEI GRANDI NUMERI

Alcuni richiami alla probabilità TEOREMI LIMITE TEOREMA DEL LIMITE CENTRALE Se Xi i=1, … è una successione di variabili indipendenti e identicamente distribuite di media e varianza 2 finita allora converge in distribuzione ad una v. c. N(0, 1)

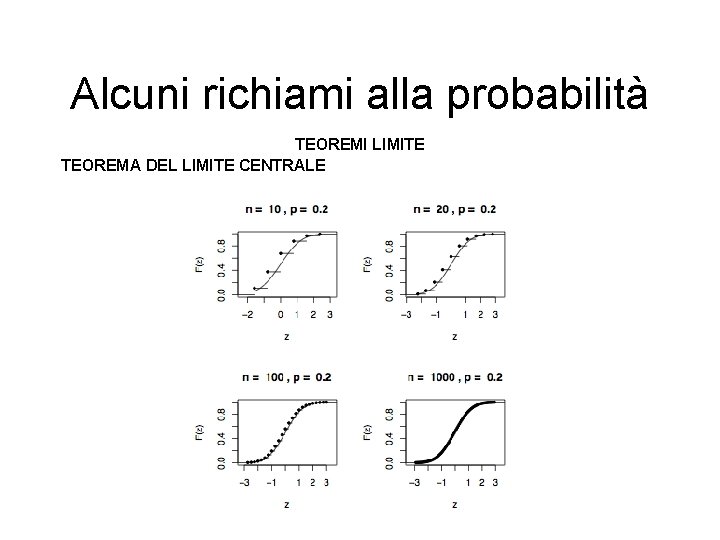
Alcuni richiami alla probabilità TEOREMI LIMITE TEOREMA DEL LIMITE CENTRALE Verifichiamola ancora empiricamente con R Partiamo generando n valori casuali ad esempio da una distribuzionie Binomiale. Sia Xi ~ ß(1, 0. 2) e quindi s 2=Var(Xi)=p(1 -p)=0. 16 all’aumentare di n a cosa converge? Ø par(mfrow=c(2, 2)) > p<-0. 2 > nobs<-c(10, 20, 1000) > par(mfrow=c(2, 2)) > for (n in nobs) { y<-0: n prob<-pbinom(y, n, p) z<-(y/n-p)*sqrt(n)/sqrt(p*(1 -p)) ind<-(z>-3)&( z<3) z<-z[ind] prob<-c(0, prob[ind]) plot(stepfun(z, prob, f = 0), verticals=FALSE, pch=20, main=paste("n = ", n , ", p = ", p), ylab="F(z)", xlab="z") curve(pnorm(x), from=min(z), to=max(z), add=TRUE)}

Alcuni richiami alla probabilità TEOREMI LIMITE TEOREMA DEL LIMITE CENTRALE

Statistica descrittiva vs Statistica inferenziale

Statistica descrittiva: organizzazione tabellare e grafica • Aiutiamoci ancora con R…. • Prendiamo un insieme di dati che ci accompagneranno in questo viaggio… • In un reparto dove si assemblano walkman vengono provate in tre giorni diversi tre differenti linee di produzione. Le tre diverse organizzazioni sono chiamate: vecchia, nuova 1 e nuova 2. Nei tre giorni per i 288 dipendenti viene rilevato il numero di operazioni completato Qual’è l’organizzazione migliore? Carichiamo il file org. txt > dati<-read. table(file="org. txt", header=TRUE) > names(dati) > dati[1: 19, ] Questo è un dataframe dove ogni riga è una unità statistica e ogni colonna è una variabile misurata sulle unità statistiche e può contenere variabili numeriche o categoriali

Statistica descrittiva: organizzazione tabellare e grafica oper org 1 694 vecchia 2 704 nuova 1 3 696 vecchia 4 698 vecchia 5 710 nuova 2 6 696 nuova 1 7 707 vecchia 8 684 nuova 1 9 690 vecchia 10 699 nuova 2 11 711 nuova 2 12 739 nuova 1 13 711 nuova 1 14 707 vecchia 15 680 nuova 1 16 698 nuova 2 17 744 nuova 2 18 713 vecchia 19 744 nuova 1

Statistica descrittiva: organizzazione tabellare e grafica > attach(dati) > vecchia<-oper[org == 'vecchia'] > nuova 1<-oper[org == 'nuova 1'] > nuova 2<-oper[org == 'nuova 2'] > vecchia[1: 30] Questi dati non sono moltissimi ma sono abbastanza per poterli solo guardare. Quindi abbiamo bisogno di “sintetizzarli” e capirli meglio…. . FREQUENZE ASSOLUTE Un primo tentaitivo può essere quello di dividere i dati in classi e di contare le frequenze per classe ossia quanti dati vanno a finire in ogni classe > classi <-670+5*(0: 18) >classi [1] 670 675 680 685 690 695 700 705 710 715 720 725 730 735 740 745 750 755 760 Øcut. op<-cut(vecchia, breaks=classi, right = FALSE) #assegniamo gli operai della vecchia organizzazione ad ogni classe

Statistica descrittiva: organizzazione tabellare e grafica > table(cut. op)%creiamo la tabella di frequenza cut. op [670, 675) [675, 680) [680, 685) [685, 690) [690, 695) [695, 700) 0 2 4 13 23 35 [700, 705) [705, 710) [710, 715) [715, 720) [720, 725) 55 52 50 33 15 [725, 730) [730, 735) [735, 740) [740, 745) [745, 750) [750, 755) 6 0 0 0 [755, 760) 0 >table(cut(vecchia, breaks=10)) #qui è R che divide liberamente in classi ma il numero delle classi glielo passiamo noi.

Statistica descrittiva: organizzazione tabellare e grafica

Statistica descrittiva: organizzazione tabellare e grafica FREQUENZE RELATIVE • Dividendo le frequenze assolute per il numero totale di unità statistiche (288 addetti!!) si ottengono le frequenze relative > n<-length(cut. op) >round(table(cut. op)/n, 3) cut. op [670, 675) [675, 680) [680, 685) [685, 690) [690, 695) [695, 700) 0. 000 0. 007 0. 014 0. 045 0. 080 0. 122 [700, 705) [705, 710) [710, 715) [715, 720) [720, 725) 0. 191 0. 181 0. 174 0. 115 0. 052 [725, 730) [730, 735) [735, 740) [740, 745) [745, 750) [750, 755) 0. 021 0. 000 [755, 760) 0. 000

Statistica descrittiva: organizzazione tabellare e grafica FREQUENZE ASSOLUTE E FREQUENZE RELATIVE Rigorosamente:

Statistica descrittiva: organizzazione tabellare e grafica ISTOGRAMMA Ci può essere molto utile rappresentare graficamente ciò che abbiamo visto prima in numeri >par(mfrow=c(3, 1)) >hist(vecchia) >hist(nuova 1) >hist(nuova 2) • Base dei rettangoli = intervalli riportati nella 1 colonna della tabella precedente • Altezza rettangoli = frequenze assolute

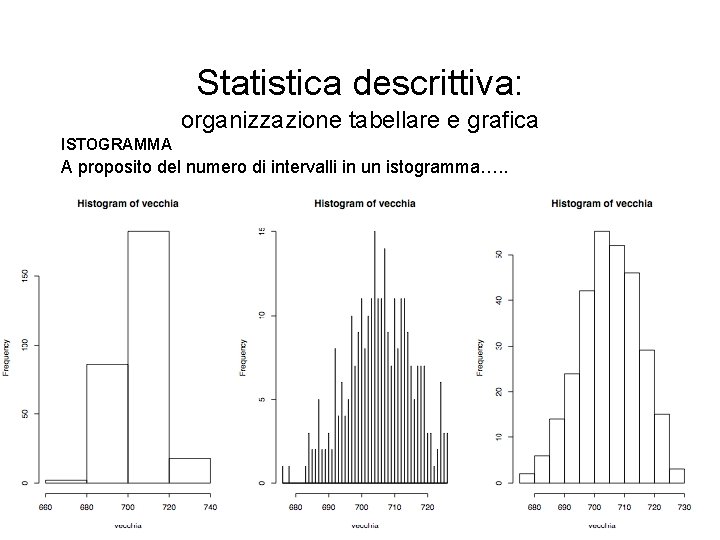
Statistica descrittiva: organizzazione tabellare e grafica ISTOGRAMMA A proposito del numero di intervalli in un istogramma…. . Abbiamo osservato che è assolutamente arbitrario scegliere quanti e quali intervalli utilizzare…ma è facile capire che pochi intervalli danno poche informazioni e troppi intervalli? ? Un numero ragionevole di intervalli introduce meno rumore…. . Quindi è meglio provare differenti lunghezze per gli intervalli anche in funzione del numero dei dati…. Esistono alcune regolette Ma è meglio usarle come punto di partenza….

Statistica descrittiva: organizzazione tabellare e grafica ISTOGRAMMA A proposito del numero di intervalli in un istogramma…. .

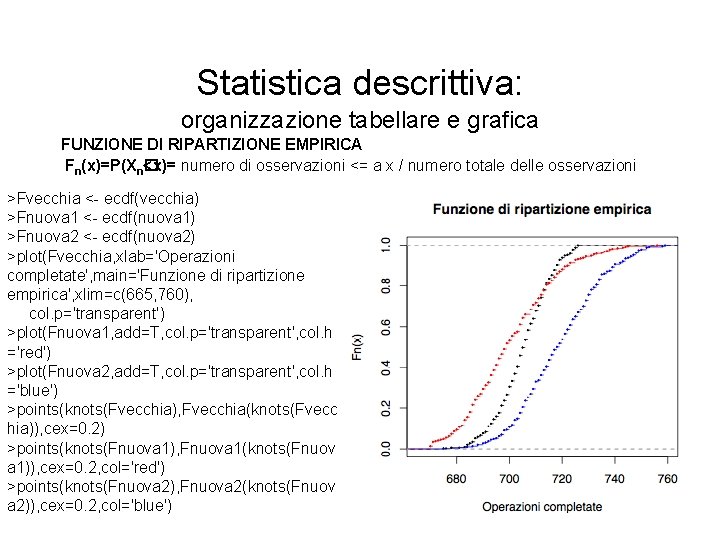
Statistica descrittiva: organizzazione tabellare e grafica FUNZIONE DI RIPARTIZIONE EMPIRICA Fn(x)=P(Xn� <x)= numero di osservazioni <= a x / numero totale delle osservazioni >Fvecchia <- ecdf(vecchia) >Fnuova 1 <- ecdf(nuova 1) >Fnuova 2 <- ecdf(nuova 2) >plot(Fvecchia, xlab='Operazioni completate', main='Funzione di ripartizione empirica', xlim=c(665, 760), col. p='transparent') >plot(Fnuova 1, add=T, col. p='transparent', col. h ='red') >plot(Fnuova 2, add=T, col. p='transparent', col. h ='blue') >points(knots(Fvecchia), Fvecchia(knots(Fvecc hia)), cex=0. 2) >points(knots(Fnuova 1), Fnuova 1(knots(Fnuov a 1)), cex=0. 2, col='red') >points(knots(Fnuova 2), Fnuova 2(knots(Fnuov a 2)), cex=0. 2, col='blue')

Statistica descrittiva: Misure di posizione Ma di quanto l’organizzazione Nuova 2 è migliore delle altre? Ci sono dei numeri che indicano dove la distribuzione è posizionata? Noti parametri di posizione sono: • La media aritmetica • La mediana • I quantili

Statistica descrittiva: Misure di posizione MEDIA ARITMETICA Supponiamo di avere n unità statistiche su cui abbiamo osservato i valori y 1, , , yn La media aritmetica dei dati è: >mean(vecchia) [1] 705. 4722

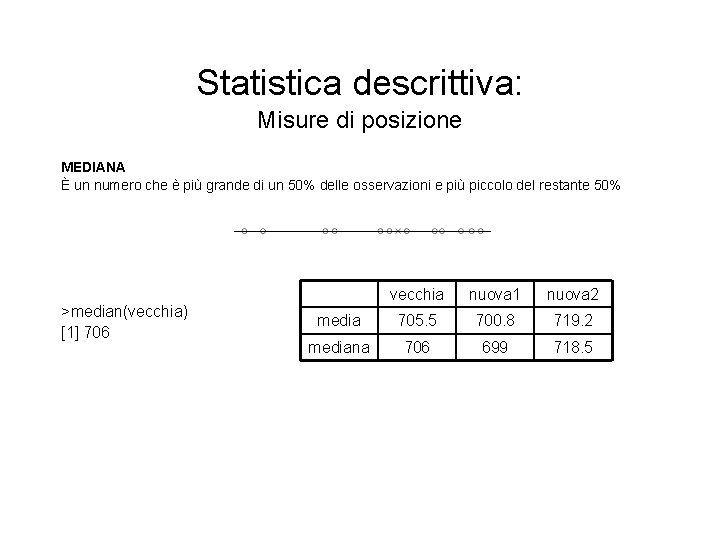
Statistica descrittiva: Misure di posizione MEDIANA È un numero che è più grande di un 50% delle osservazioni e più piccolo del restante 50% >median(vecchia) [1] 706 vecchia nuova 1 nuova 2 media 705. 5 700. 8 719. 2 mediana 706 699 718. 5

Statistica descrittiva: Misure di posizione QUANTILI Generalizzano il concetto di mediana poichè l’idea alla base di un quantile p dove 0<p<1 è di cercare un numero che sia più grande del 100 x p% dei dati osservati e più piccolo del restante 100 x (1 -p)%. Ad esempio il quantile 0. 1 è un valore che lascia a sinistra il 10% delle osservazioni e a destra il 90%. I quantili più noti sono i quartili ossia con p uguale a 0. 25, 0. 50, 0. 75 e sono detti così perchè dividono la popolazione in quattro parti. Domandina: Chi è il secondo quartile? ? >quantile(vecchia, probs = c(0. 25, 0. 50, 0. 75)) 25% 50% 75% 699 706 713 >summary(vecchia) Min. 1 st Qu. Median Mean 3 rd Qu. Max. 676. 0 699. 0 706. 0 705. 5 713. 0 726. 0

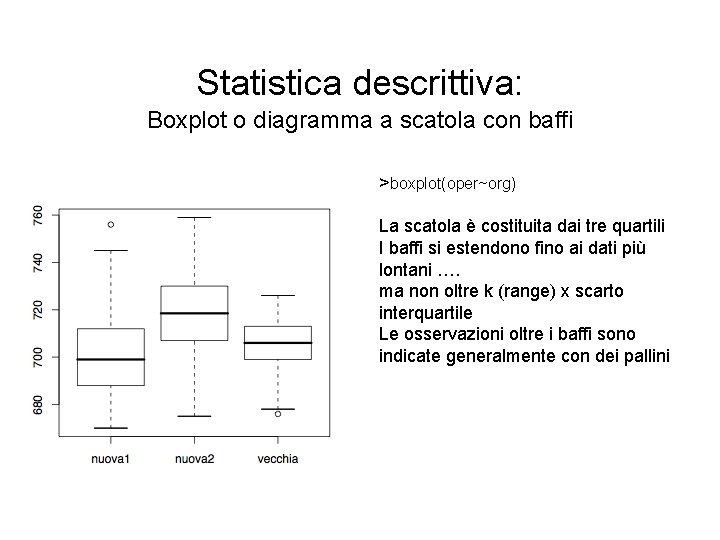
Statistica descrittiva: Boxplot o diagramma a scatola con baffi >boxplot(oper~org) La scatola è costituita dai tre quartili I baffi si estendono fino ai dati più lontani …. ma non oltre k (range) x scarto interquartile Le osservazioni oltre i baffi sono indicate generalmente con dei pallini

Statistica descrittiva: Boxplot o diagramma a scatola con baffi Attenzione però: interpretiamo bene i dati Solo a titolo indicativo mostriamo due distribuzioni A e B… fondamentalmente hanno la stessa media… Ma secondo voi cosa cambia? ? Così la smettiamo con la storia dei polli di Trilussa….

Statistica descrittiva: Indici di variabilità Tra gli indici che ci permettono di valutare sinteticamente la variabilità di un insieme di dati vi sono: • La varianza • Lo scarto quadratico medio • Il campo di variazione • Lo scarto interquartile • MAD

Statistica descrittiva: Indici di variabilità VARIANZA Mi dice in pratica quanto i dati distano o si disperdono dalla media aritmetica Attenzione la funzione var() di R calcola la varianza campionaria e non quella della popolazione Quindi var(y) lo otteniamo come (n-1)*var(y)/n

Statistica descrittiva: Indici di variabilità SCARTO QUADRATICO MEDIO Mentre l’unità di misura della varianza è uguale al quadrato dell’unità di misura dei dati originali l’unità di misura dello squarto quadratico medio coincide con quella dei dati

Statistica descrittiva: Indici di variabilità CAMPO DI VARIAZIONE In R range() SCARTO INTERQUARTILE MAD Median Absolute Deviation In R MAD<-function(x) { a<-median(abs(x-median(x))) return(a) }

Statistica descrittiva: Indici di variabilità COEFFICIENTE DI VARIAZIONE / Restituisce una misura della variabilità ‘aggiustata’ per tener conto delle differenti unità di misura dei fenomeni

Statistica descrittiva: I DATI QUALITATIVI Consideriamo il file “laureati. txt” >laureati<-read. table("laureati. txt", header=TRUE) >names(laureati) [1] "corso" "matricola" "sesso" "provincia" "anno" "tipo" "diploma" "votomat" "base" “votolau" "lode" >attach(laureati) >table(provincia) provincia BL BZ CH CO CT FE FG GO PD PN RO TN TS TV UD VE VI VR 8 2 1 1 1 2 1 1 69 7 4 2 1 163 3 169 25 7 >table(sesso) sesso F M 281 186 Media e varianza non hanno senso in questo caso…useremo la moda ossia la modalità con la frequenza più alta: >which. max(table(provincia)) VE 16 >max(table(provincia)) [1] 169

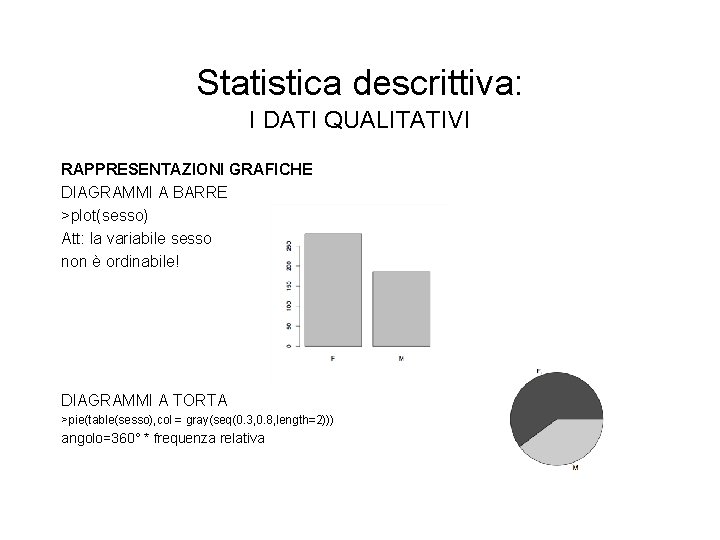
Statistica descrittiva: I DATI QUALITATIVI RAPPRESENTAZIONI GRAFICHE DIAGRAMMI A BARRE >plot(sesso) Att: la variabile sesso non è ordinabile! DIAGRAMMI A TORTA >pie(table(sesso), col = gray(seq(0. 3, 0. 8, length=2))) angolo=360° * frequenza relativa

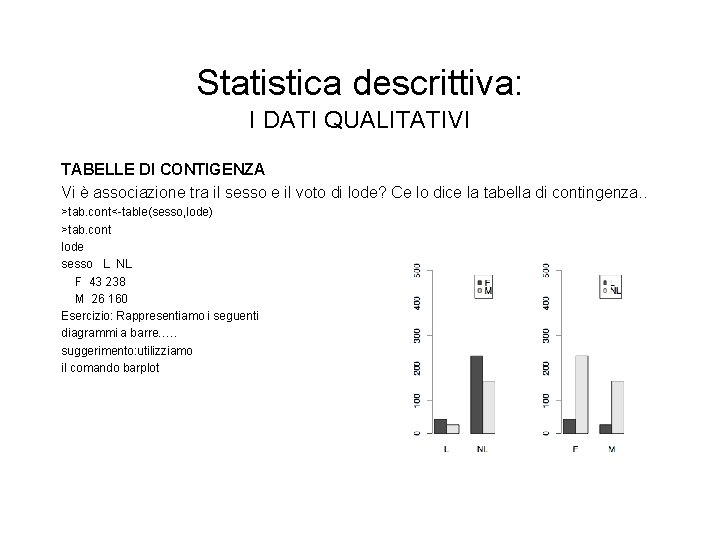
Statistica descrittiva: I DATI QUALITATIVI TABELLE DI CONTIGENZA Vi è associazione tra il sesso e il voto di lode? Ce lo dice la tabella di contingenza. . >tab. cont<-table(sesso, lode) >tab. cont lode sesso L NL F 43 238 M 26 160 Esercizio: Rappresentiamo i seguenti diagrammi a barre…. . suggerimento: utilizziamo il comando barplot

Statistica descrittiva: COVARIANZA E CORRELAZIONE >data(swiss) >names(swiss) [1] "Fertility" "Agriculture" "Examination" "Education" >attach(swiss) >log. Education<-log(Education) >indicators<-cbind(Fertility, Agriculture, log. Education) >pairs(indicators) Come misuriamo la direzione e la forza delle relazioni tra le variabili? >n<-length(Fertility) >cov(indicators)*(n-1)/n Fertility Agriculture log. Education Fertility 152. 722445 98. 03789 -5. 0856329 Agriculture 98. 037890 504. 82496 -11. 9200088 log. Education -5. 085633 -11. 92001 0. 6160699 "Catholic" "Infant. Mortality”

Statistica descrittiva: COVARIANZA E CORRELAZIONE COVARIANZA Osservazioni: 1) Se a valori crescenti di X corrispondono valori crescenti di Y ci aspettiamo che valori della media di X corrispondano a valori maggiori della media di Y perciò la covarianza sarà positiva; 2) Se al contrario al crescere della X la Y descresce ci aspettiamo una covarianza negativa; 3) Più è forte la relazione tra le due variabili più la covarianza sarà grande in valore assoluto mentre in assenza di una relazione monotona tra le due variabili la covarianza sarà vicina allo zero. Quindi useremo la covarianza per misurare la DIREZIONE della relazione esistente tra due variabili E per misurare la FORZA della relazione esistente? ? Attenzione come per la var la funzione cov() di R calcola la covarianza campionaria Quindi cov(x, y) lo otteniamo come (n-1)*cov(x, y)/n

Statistica descrittiva: COVARIANZA E CORRELAZIONE (LINEARE) >cor(indicators) Fertility Agriculture log. Education Fertility 1. 0000000 0. 3530792 -0. 5242985 Agriculture 0. 3530792 1. 0000000 -0. 6759136 log. Education -0. 5242985 -0. 6759136 1. 0000000 Spesso indicato anche con r tale coefficiente varia tra -1 e 1. In particolare: se cor(X, Y)>0 la relazione tra le due variabili è positiva ed è tanto più forte tanto più si avvicina ad 1; se cor(X, Y)<0 l’associazione tra i dati è negativa; se cor(X, Y)= 1 allora i dati sono perfettamente allineati su di una retta con coeff angolare positivo o negativo; Se cor(X. Y)=0 allora non esiste una relazione di tipo lineare (e più in generale un’associazione monotona) tra le variabili

Statistica descrittiva: COVARIANZA E CORRELAZIONE

Domande?