Elementi di Statistica descrittiva Lez 3 Gli Indici

Elementi di Statistica descrittiva Lez. 3 - Gli Indici di VARIABILITA’ - Campo di variazione Scarto dalla media Varianza Scarto quadratico medio Coefficiente di variazione 1

Indici di Variabilità I valori medi sono indici importanti per la descrizione sintetica di un fenomeno statistico Hanno però il limite di non darci alcuna informazione sulla distribuzione dei dati 2

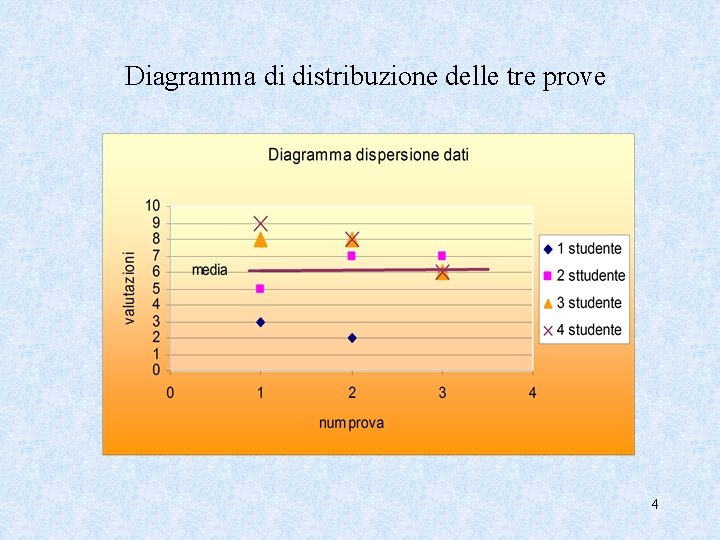
Esempio In tre differenti prove di matematica 4 studenti hanno riportato le seguenti valutazioni In tutte e tre le prove la media è 6, 25 ma i dati sono chiaramente distribuiti in modo diverso 3

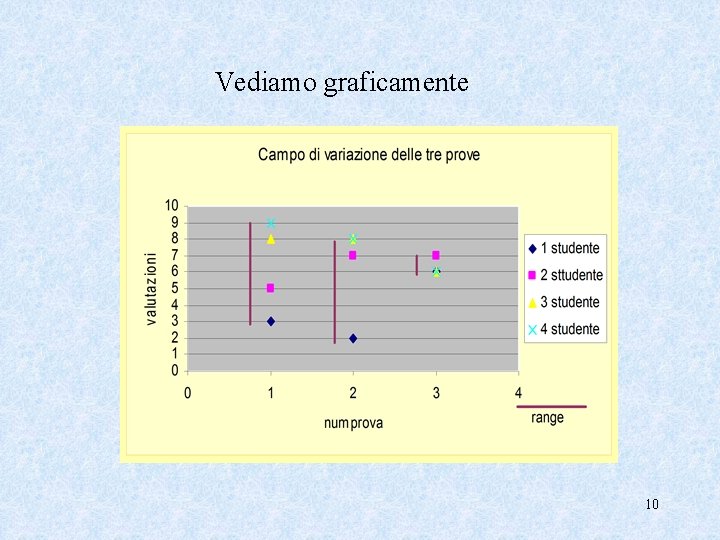
Diagramma di distribuzione delle tre prove 4

• nel caso della 1 a prova e 2 a prova sarà opportuno fare un recupero per alcuni studenti • nel caso della 3 a prova l’insegnante può ritenere che gli obiettivi siano stati raggiunti dalla classe, anche se ad un livello solo sufficiente 5

In statistica è possibile valutare in modo sintetico la distribuzione dei dati mediante gli indici di variabilità (o dispersione) Vedremo i seguenti indici • • Campo di variazione (Range) Scarto medio dalla media Varianza e scarto quadratico medio Coefficiente di variazione 6

Campo di variazione E’ il più semplice degli indici di variazione: Si calcola facendo la differenza tra il dato più grande e il dato più piccolo Campo variazione = x max – x min Rappresenta l’ampiezza dell’intervallo dei dati 7

Esempio Consideriamo le valutazioni della prima prova Xmax = 9; Xmin = 3 Range = 9 – 3 = 6 8

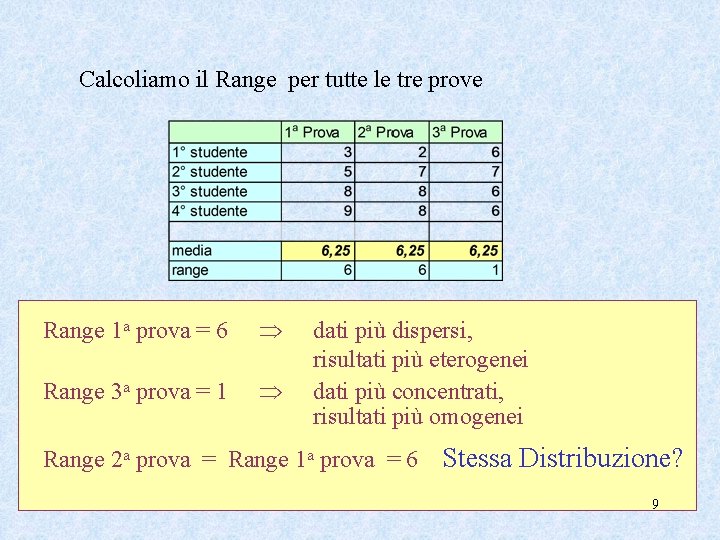
Calcoliamo il Range per tutte le tre prove Range 1 a prova = 6 Range 3 a prova = 1 dati più dispersi, risultati più eterogenei dati più concentrati, risultati più omogenei Range 2 a prova = Range 1 a prova = 6 Stessa Distribuzione? 9

Vediamo graficamente 10

Osservazioni: 1. Il campo di variazione dà informazioni sulla distribuzione dei dati: • più R è piccolo più i dati sono concentrati; • più R è grande più i dati sono dispersi. 2. R è espresso nella stessa unità di misura dei dati 3. Tuttavia R tiene conto solo dei dati estremi della distribuzione e non di tutti i dati, pertanto distribuzioni diverse ma con gli stessi valori estremi hanno range uguali Es. Range 1 aprova = Range 2 a prova. ma distribuzione 1 a prova Distribuzione 2 a prova 11

Scarto medio dalla media aritmetica Un altro modo per calcolare la variabilità dei dati (tenendo conto di tutti i dati) consiste nel calcolare la distanza di tutti i dati dalla media e fare la media aritmetica di tali distanze Scarto medio = Distanza media dei dati dalla media 12

Esempio Consideriamo le valutazioni della prima prova x 1 = 3 – 6, 25 = 3, 25; x 2 = 5 – 6, 25 = 1, 25; x 3 = 8 – 6, 25 = 1, 75; x 4 = 9 – 6, 25 = 2, 75; Sm = 3, 25 + 1, 75 + 2, 75 = 2, 25 4 13

Calcoliamo lo Scarto medio per tutte le tre prove Scarto 1 a prova = 2, 25 Scarto 3 a prova = 0, 38 Scarto 2 a pr. Scarto 1 a pr. dati più dispersi, risultati più eterogenei dati più concentrati, risultati più omogenei “Le Distribuzioni Differiscono” 14

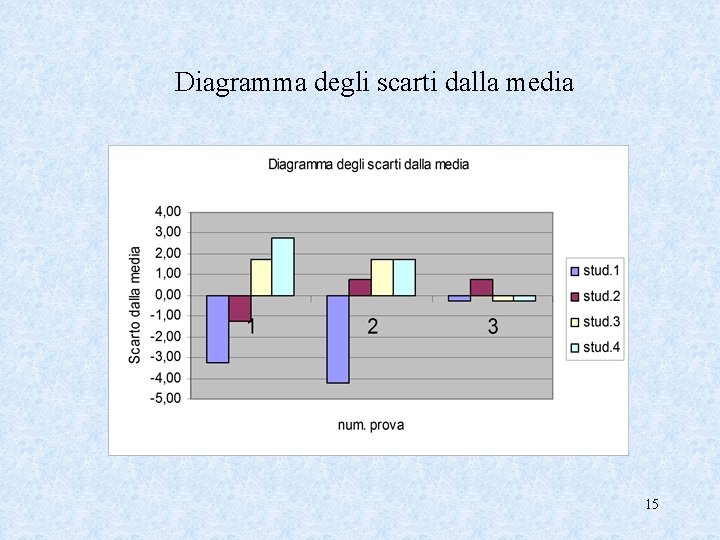
Diagramma degli scarti dalla media 15

Osservazioni: 1. Lo scarto medio dalla media dà informazioni sulla distribuzione dei dati: • più SM è piccolo più i dati sono concentrati; • più SM è grande più i dati sono dispersi. 2. SM è espresso nella stessa unità di misura dei dati 3. Non ha l'inconveniente del “Campo di variazione” in quanto SM tiene conto di tutti i dati della distribuzione 16

Varianza e Scarto quadratico medio Sono gli indici di variabilità più utilizzati, e tengono conto della distribuzione di tutti i dati. Varianza Rappresenta la media aritmetica dei quadrati delle distanze dei dati dalla media M 17

18

Esempio - Varianza Consideriamo le valutazioni della prima prova ( x 1)2 = (3 – 6, 25 )2 = 10, 5625; ( x 2)2 = (5 – 6, 25 )2 = 1, 5625; ( x 3)2 = (8 – 6, 25 )2 = 3, 0625; ( x 4)2 = (9 – 6, 25 )2 = 7, 5625; 2 = 10, 5625+1, 5625+3, 0625+7, 5625 = 5, 6875 4 19

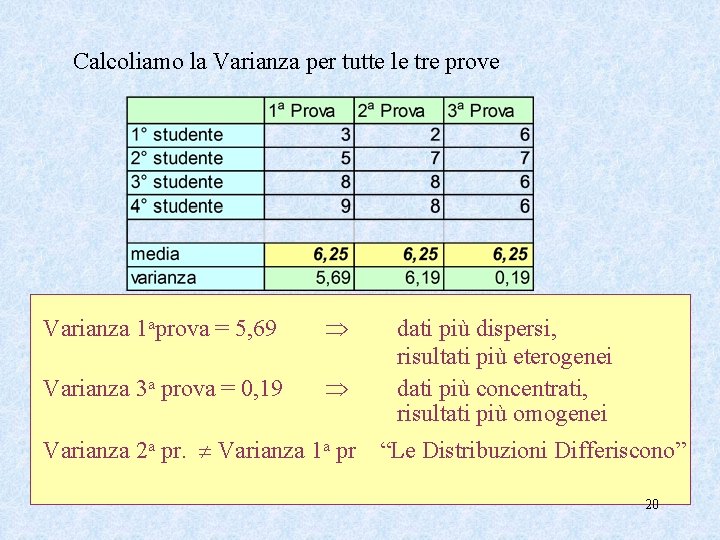
Calcoliamo la Varianza per tutte le tre prove Varianza 1 aprova = 5, 69 Varianza 3 a prova = 0, 19 Varianza 2 a pr. Varianza 1 a pr dati più dispersi, risultati più eterogenei dati più concentrati, risultati più omogenei “Le Distribuzioni Differiscono” 20

Scarto quadratico medio o Deviazione standard È uguale alla radice quadrata della varianza 21

Esempio - Scarto quadratico medio Riprendiamo le valutazioni della prima prova 22

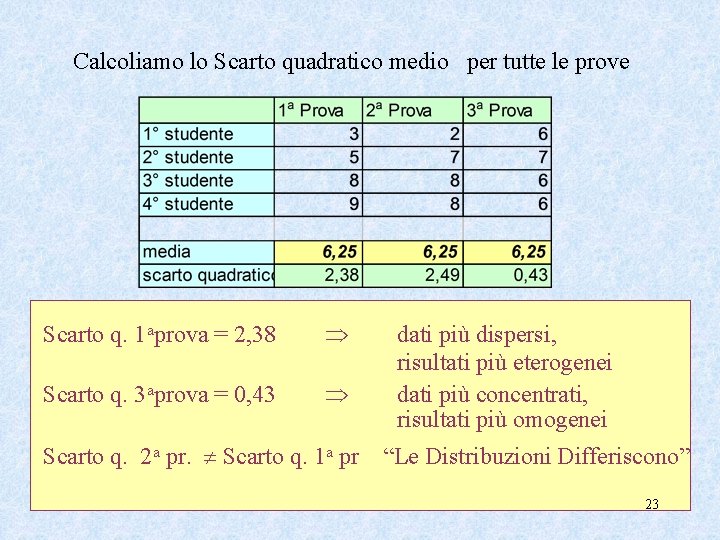
Calcoliamo lo Scarto quadratico medio per tutte le prove Scarto q. 1 aprova = 2, 38 Scarto q. 3 aprova = 0, 43 Scarto q. 2 a pr. Scarto q. 1 a pr dati più dispersi, risultati più eterogenei dati più concentrati, risultati più omogenei “Le Distribuzioni Differiscono” 23

Osservazioni: 1. La varianza 2 e lo scarto quadratico medio danno informazioni sulla distribuzione dei dati: • più 2 e sono piccoli più i dati sono concentrati; • più 2 e sono grandi più i dati sono dispersi. 2. Entrambi gli indici tengono conto di tutti i dati della distribuzione 24

3. Entrambi si basano sulla proprietà della media per cui la somma dei quadrati degli scarti dalla media è minima 4. La varianza è espressa mediante il quadrato dell’unità di misura dei dati 5. Lo scarto quadratico nella stessa unità di misura dei dati e pertanto viene preferito alla varianza 25

Il coefficiente di variazione CV Il CV è una misura relativa di dispersione (le precedenti sono misure assolute) ed è una grandezza adimensionale. E’ particolarmente utile quando si devono confrontare le distribuzioni di due gruppi con medie molto diverse o con dati espressi in scale differenti (es. confronto tra variazione del peso e variazione dell’altezza). 26

In natura il coeff. di variazione tende a rimanere costante per ogni fenomeno: i valori normalmente variano dal 5% al 15% Se i valori di CV sono esterni a quelli indicati o si è in presenza di errori di rilevazione, oppure il fenomeno presenta aspetti particolari. • se CV è molto basso (2 – 3 %) bisogna sospettare l’esistenza di fattori limitanti la variabilità, • se CV è molto alto (intorno al 40% o più) è molto probabile l’esistenza di fattori che aumentano la variabilità 27

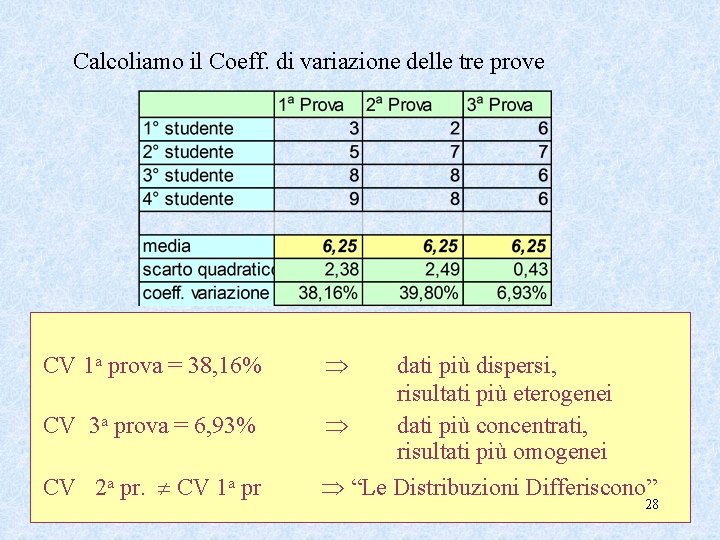
Calcoliamo il Coeff. di variazione delle tre prove CV 1 a prova = 38, 16% CV 3 a prova = 6, 93% CV 2 a pr. CV 1 a pr “Le Distribuzioni Differiscono” dati più dispersi, risultati più eterogenei dati più concentrati, risultati più omogenei 28

Un esempio: la distribuzione normale 29

Le misure di Forma Sono indici sintetici utilizzati per evidenziare particolarità nella forma della distribuzione. Noi esamineremo: • l’asimmetria • la curtosi 30

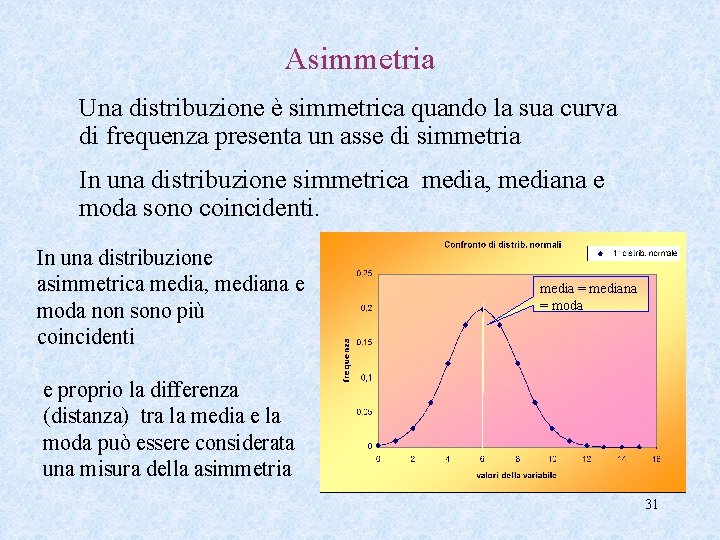
Asimmetria Una distribuzione è simmetrica quando la sua curva di frequenza presenta un asse di simmetria In una distribuzione simmetrica media, mediana e moda sono coincidenti. In una distribuzione asimmetrica media, mediana e moda non sono più coincidenti media = mediana = moda e proprio la differenza (distanza) tra la media e la moda può essere considerata una misura della asimmetria 31

Sono state proposte diverse misure dell’ asimmetria, per esempio le più semplici sono: Dette rispettivamente: primo e secondo coeff. di asimmetria di Pearson Un altro coeff di asimmetria è il Coeff. di asimmetria (di Fisher) = scarto quadratico medio Se a = 0 distribuzione simmetrica Se a > 0 asimmetria destra Se a < 0 asimmetria sinistra 32

Asimmetria positiva (as. Destra) La distribuzione è asimmetrica quando non presenta nessun asse di simmetria. Si ha un’asimmetria positiva o destra quando il ramo destro della curva è più lungo di quello sinistro In questo caso si ha: moda < mediana < media=63, 65 moda = 48 mediana =58 33

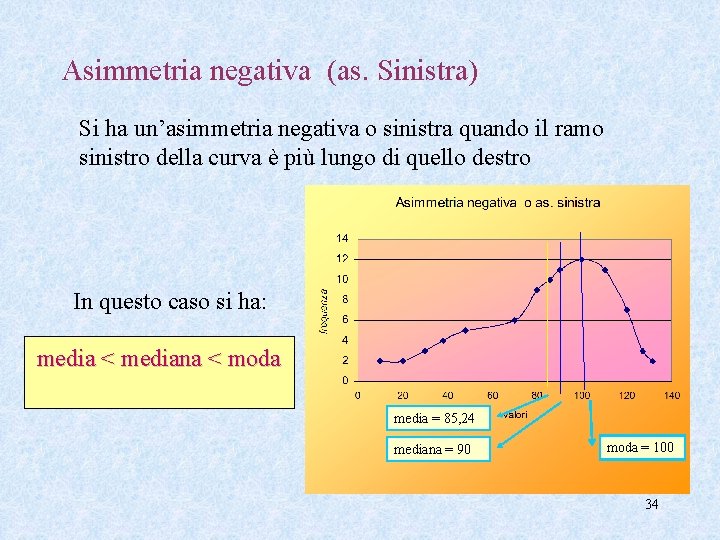
Asimmetria negativa (as. Sinistra) Si ha un’asimmetria negativa o sinistra quando il ramo sinistro della curva è più lungo di quello destro In questo caso si ha: media < mediana < moda media = 85, 24 mediana = 90 moda = 100 34

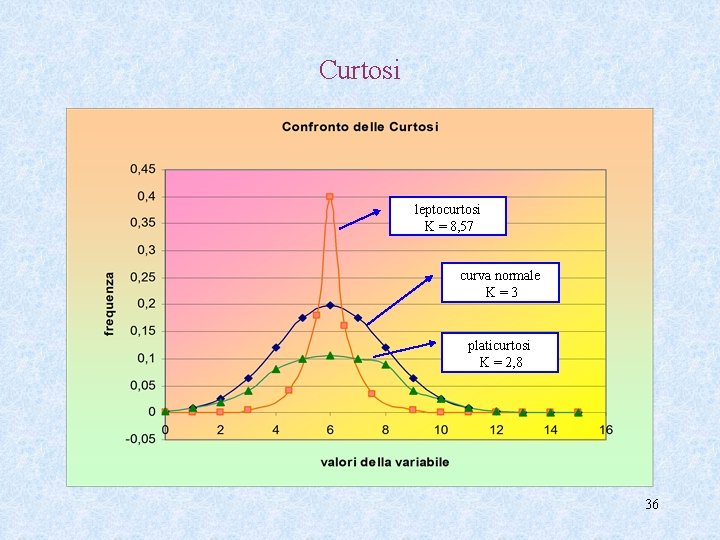
Curtosi Se una distribuzione è simmetrica o quasi simmetrica allora può esser più o meno appuntita o più o meno appiattita rispetto alla distribuzione normale (o di Gauss) Se la curva è • più appuntita si dice curva Leptocurtica • più appiattita si dice curva Platicurtica Coeff. di curtosi di Pearson = scarto quadratico medio 0 K < + inf Se K = 3 distribuzione normale se K > 3 curva leptocurtica Se K < 3 curva platicurtica. 35

Curtosi leptocurtosi K = 8, 57 curva normale K=3 platicurtosi K = 2, 8 36

Curtosi Spesso il coeff. di curtosi viene indicato con b 2 che, come visto, nel caso della distribuzione normale è = 3 pertanto, talvolta, la curtosi viene indicata con (b 2 – 3) Allora: se la distribuzione è normale (b 2 – 3 ) = 0 se la distribuzione è leptocurtica (b 2 – 3 ) > 0 se la distribuzione è platicurtica (b 2 – 3 ) < 0 37

38