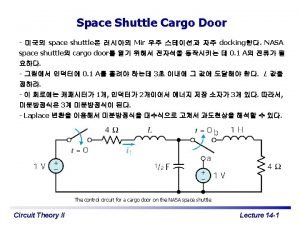
DSP C 5000 Chapter 15 Infinite Impulse Response

DSP C 5000 Chapter 15 Infinite Impulse Response (IIR) Filter Implementation

IIR Filters ESIEE, Slide 2 u Rational Z transfer function u Linear difference equation

IIR Filters – Poles and Zeros u Roots of the numerator ri are the roots of the z polynomial with bi coefficients. H(z) is null when z is equal to one of the values. They are called the zeroes of the filter and often noted by zi. u Roots of the denominator ri are the roots of the z polynomial with ai coefficients. H(z) tends to infinity when z is close to one of these values. They are called the poles of the filters and often noted by pi. ESIEE, Slide 3

Z Transfer Function w Define frequency behaviour of the filter w Consider a first order z rational filter: magnitude phase H(z) can be evaluated for each value wn from 0 to 1 with 1 corresponding to sampling frequency ESIEE, Slide 4

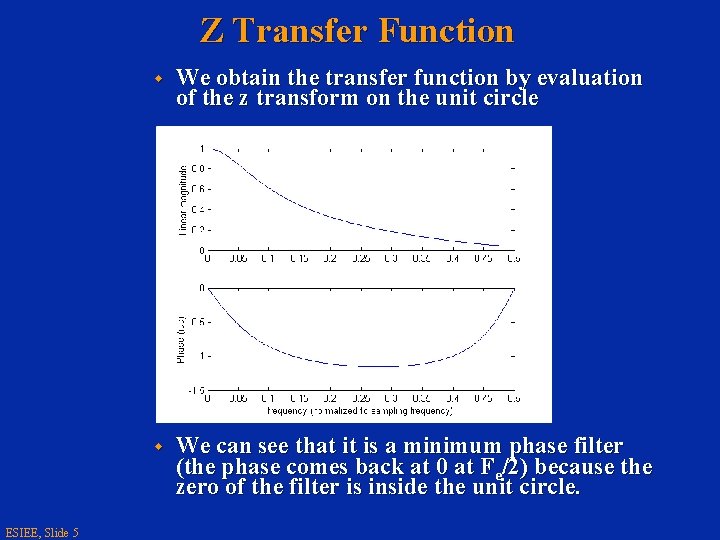
Z Transfer Function ESIEE, Slide 5 w We obtain the transfer function by evaluation of the z transform on the unit circle w We can see that it is a minimum phase filter (the phase comes back at 0 at Fe/2) because the zero of the filter is inside the unit circle.

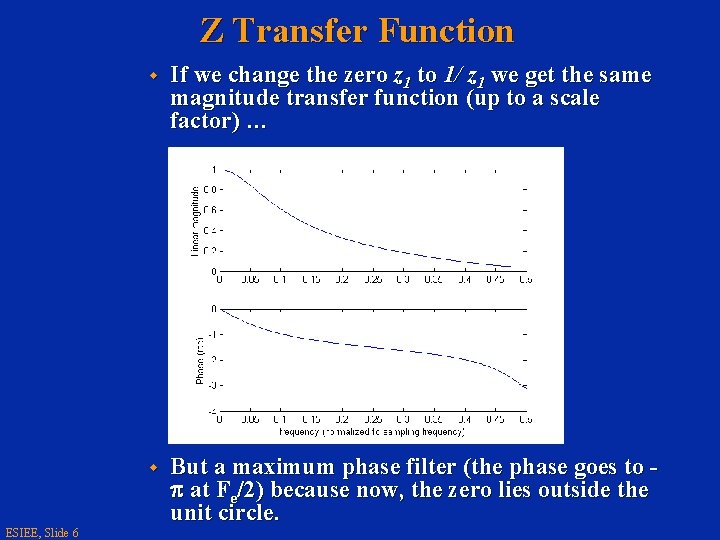
Z Transfer Function ESIEE, Slide 6 w If we change the zero z 1 to 1/ z 1 we get the same magnitude transfer function (up to a scale factor) … w But a maximum phase filter (the phase goes to p at Fe/2) because now, the zero lies outside the unit circle.

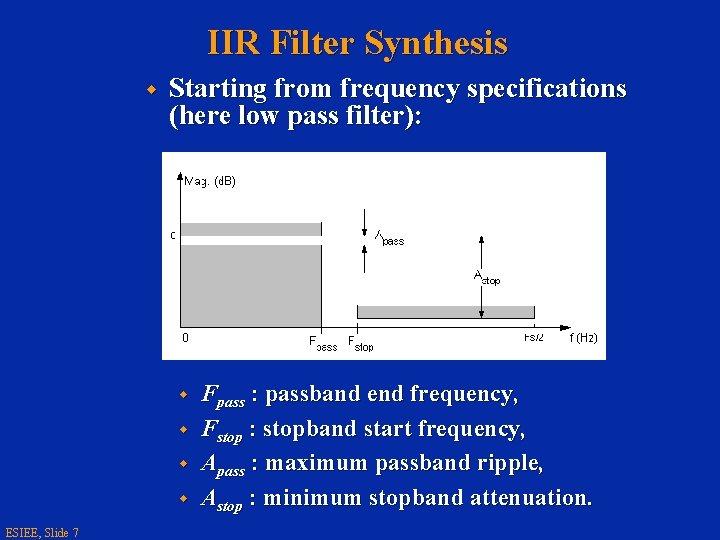
IIR Filter Synthesis w Starting from frequency specifications (here low pass filter): w w ESIEE, Slide 7 Fpass : passband end frequency, Fstop : stopband start frequency, Apass : maximum passband ripple, Astop : minimum stopband attenuation.

IIR Filters Synthesis w Analog prototype with analog to digital transformation (bilinear transform) : w w Direct digital method : Yule Walker w ESIEE, Slide 8 Digital to analog frequency specification transformation using prewarping Analog filter prototype Analog transfer function to digital transfer function transformation using bilinear transform. Try to find the recursive filter of order N which is as close as possible to the frequency specifications using the least square optimization method.

IIR Filters Synthesis u Bilinear transform : w w One to one map of analog frquencies to digital frequencies. Based on the approximation of the continuous integral operator by the trapezoïdal method. Laplace Z transform Equating integral operators, we get the bilinear transform. ESIEE, Slide 9

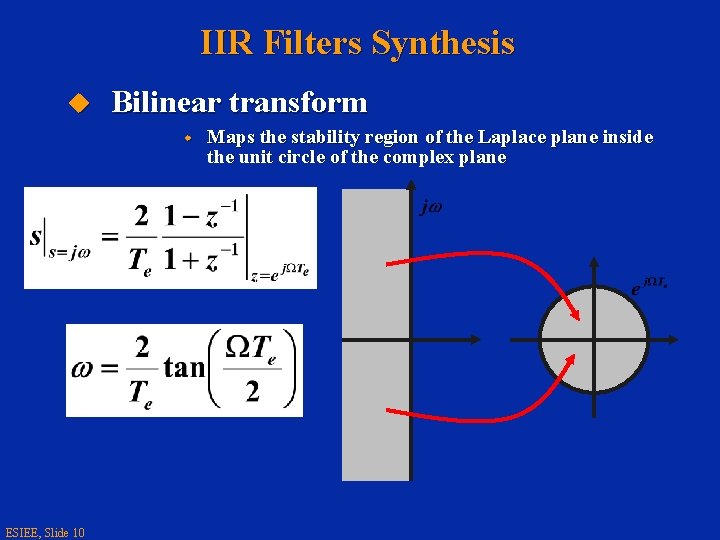
IIR Filters Synthesis u Bilinear transform w ESIEE, Slide 10 Maps the stability region of the Laplace plane inside the unit circle of the complex plane

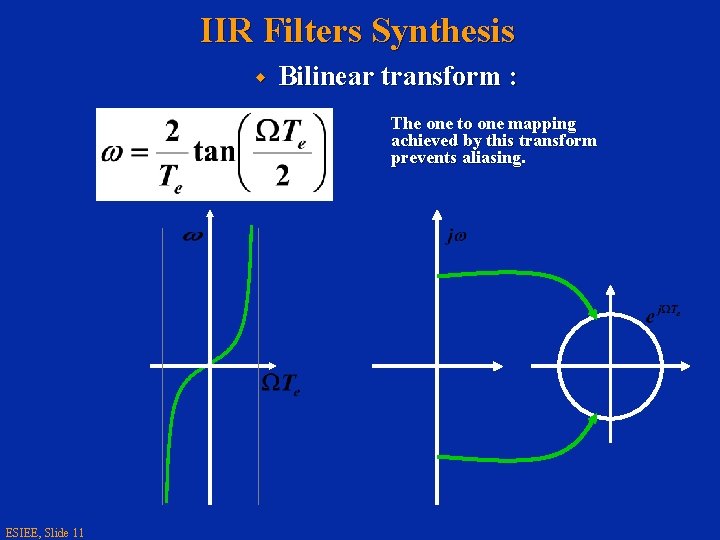
IIR Filters Synthesis w Bilinear transform : The one to one mapping achieved by this transform prevents aliasing. ESIEE, Slide 11

IIR Filters Synthesis w w Characteristics frequencies (Fp, Fa) of the target specifications have to be warped. This warped specifications is used to compute an analog prototype using approximation functions : w w w ESIEE, Slide 12 Butterworth Chebyshev II Elliptic Then the analog prototype is tranformed into a digital filter that matches target frequency specification thanks to Bilinear Transform (BT) (this cancels the warping introduce at the first step).

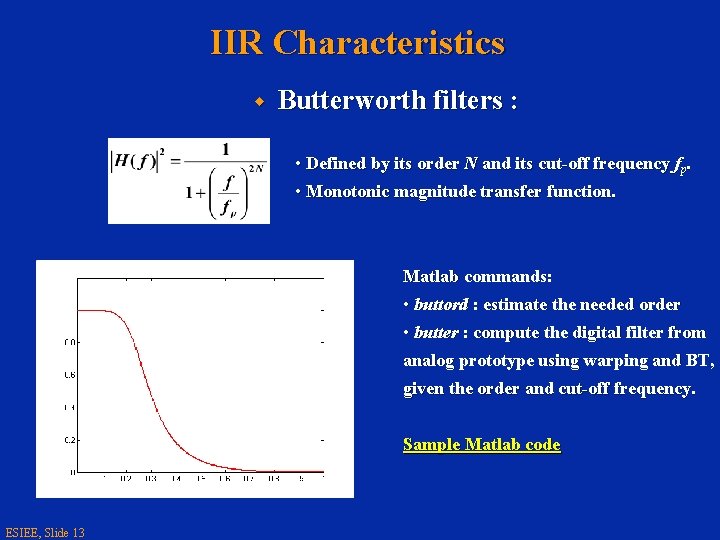
IIR Characteristics w Butterworth filters : • Defined by its order N and its cut-off frequency fp. • Monotonic magnitude transfer function. Matlab commands: • buttord : estimate the needed order • butter : compute the digital filter from analog prototype using warping and BT, given the order and cut-off frequency. Sample Matlab code ESIEE, Slide 13

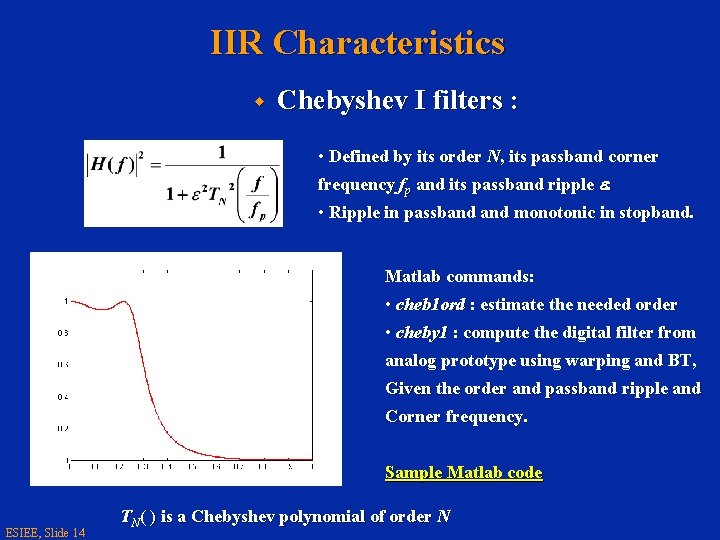
IIR Characteristics w Chebyshev I filters : • Defined by its order N, its passband corner frequency fp and its passband ripple e. • Ripple in passband monotonic in stopband. Matlab commands: • cheb 1 ord : estimate the needed order • cheby 1 : compute the digital filter from analog prototype using warping and BT, Given the order and passband ripple and Corner frequency. Sample Matlab code ESIEE, Slide 14 TN( ) is a Chebyshev polynomial of order N

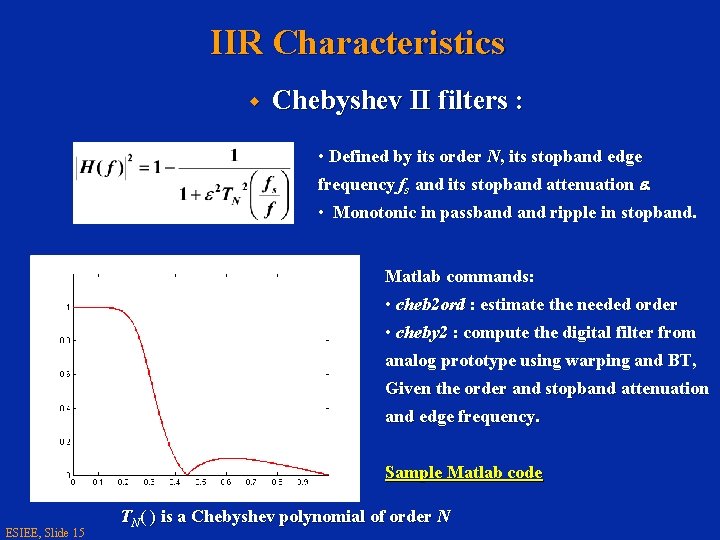
IIR Characteristics w Chebyshev II filters : • Defined by its order N, its stopband edge frequency fs and its stopband attenuation e. • Monotonic in passband ripple in stopband. Matlab commands: • cheb 2 ord : estimate the needed order • cheby 2 : compute the digital filter from analog prototype using warping and BT, Given the order and stopband attenuation and edge frequency. Sample Matlab code ESIEE, Slide 15 TN( ) is a Chebyshev polynomial of order N

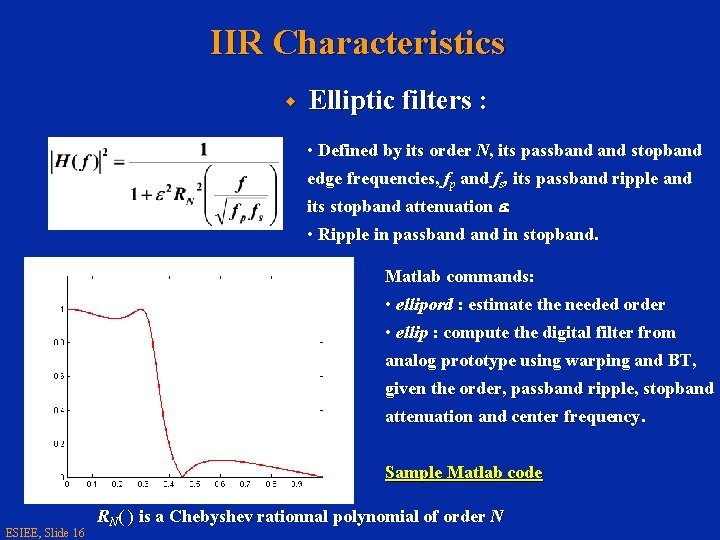
IIR Characteristics w Elliptic filters : • Defined by its order N, its passband stopband edge frequencies, fp and fs, its passband ripple and its stopband attenuation e. • Ripple in passband in stopband. Matlab commands: • ellipord : estimate the needed order • ellip : compute the digital filter from analog prototype using warping and BT, given the order, passband ripple, stopband attenuation and center frequency. Sample Matlab code ESIEE, Slide 16 RN( ) is a Chebyshev rationnal polynomial of order N

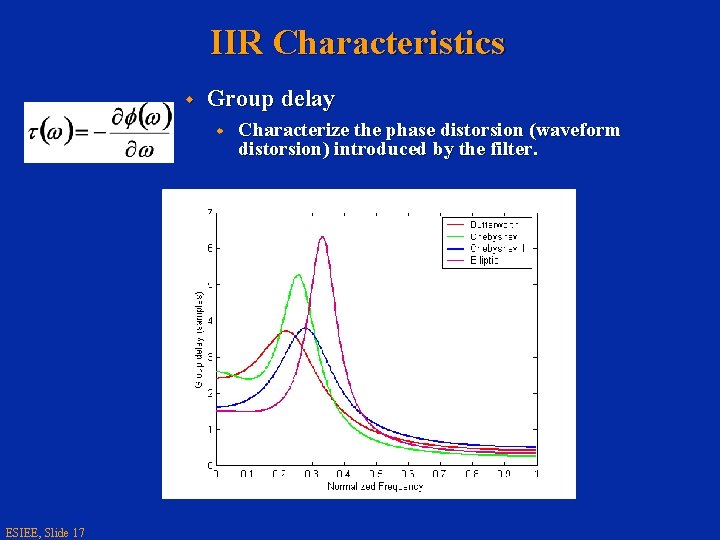
IIR Characteristics w Group delay w ESIEE, Slide 17 Characterize the phase distorsion (waveform distorsion) introduced by the filter.

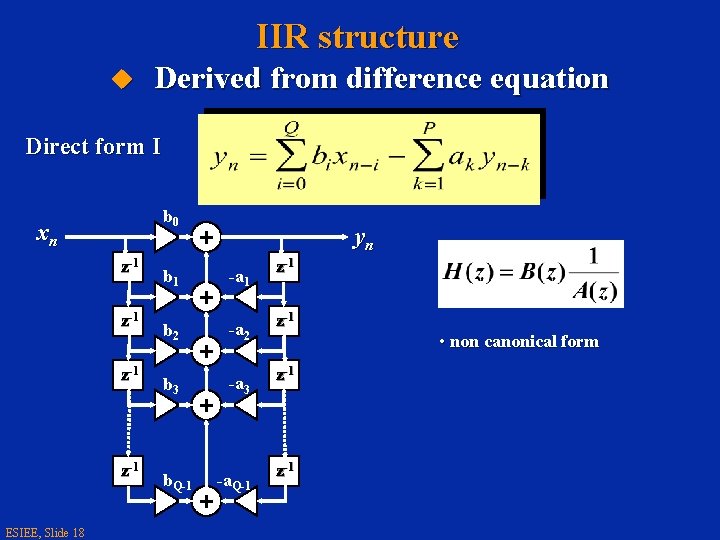
IIR structure u Derived from difference equation Direct form I b 0 xn z-1 z-1 ESIEE, Slide 18 yn z-1 b 1 -a 1 b 2 -a 2 z-1 -a 3 z-1 b 3 b. Q-1 -a. Q-1 z-1 • non canonical form

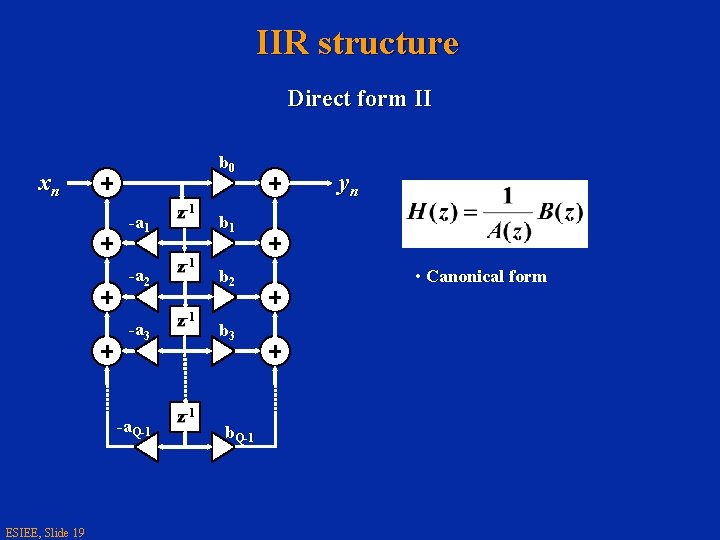
IIR structure Direct form II b 0 xn -a 1 -a 2 z-1 -a 3 z-1 -a. Q-1 ESIEE, Slide 19 z-1 yn b 1 b 2 b 3 b. Q-1 • Canonical form

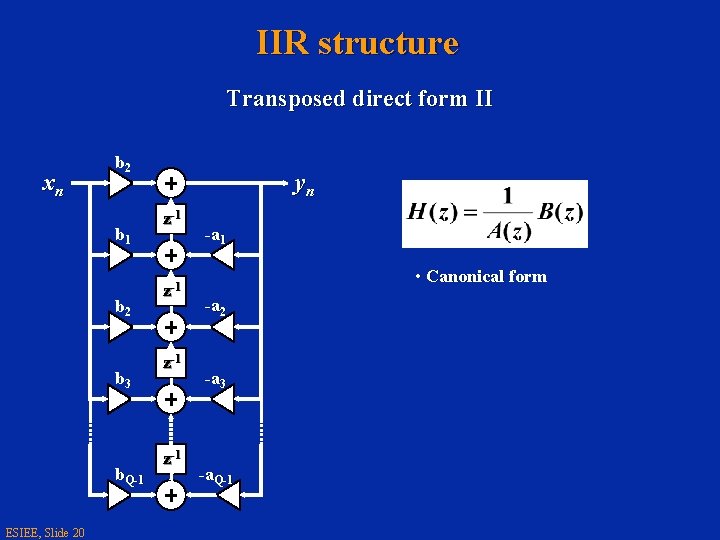
IIR structure Transposed direct form II xn b 2 b 1 b 2 b 3 b. Q-1 ESIEE, Slide 20 yn z-1 z-1 -a 1 • Canonical form -a 2 -a 3 -a. Q-1

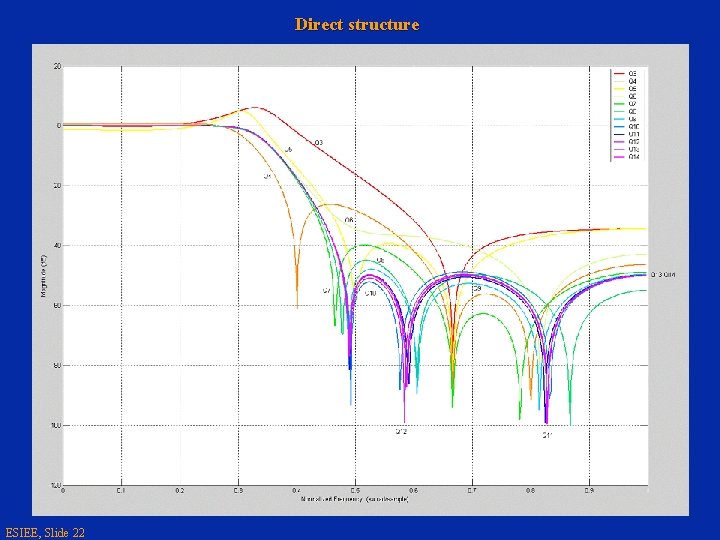
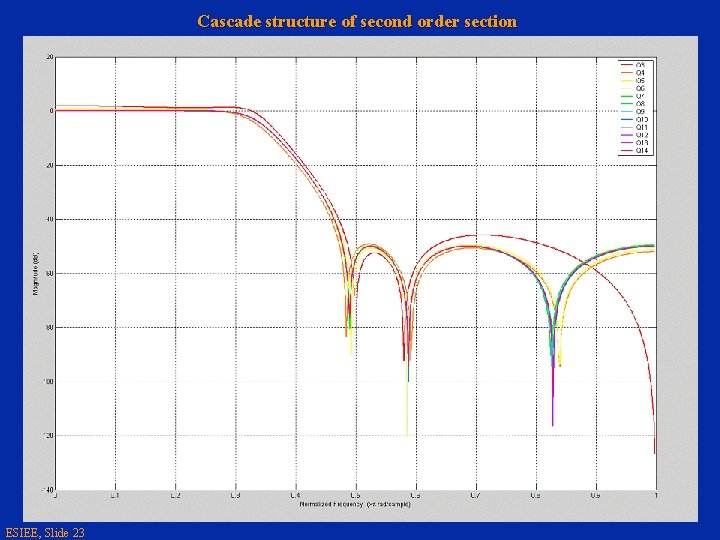
IIR – Coefficients quantization w Finite precision of DSP involves coefficients quantization: Let consider the denominator of the transfer function with , the kth quantized coefficients and Dak the quantification error. Quantized denominator is then: The resulting quantified poles will disrupt the transfer function. The higher order the polynomial is, the greater will be pertubation on its roots due to quantization. Following slides illustrate this fact: • Next slide shows the transfer function of a 6 th order direct form filter for different quantification. • Following one shows the transfer function obtained for the same filter and same quantificaiton, but with a cascade structure of second order section, this last structure is much less sensitive to quantization than the previous one. ESIEE, Slide 21

Direct structure ESIEE, Slide 22

Cascade structure of second order section ESIEE, Slide 23

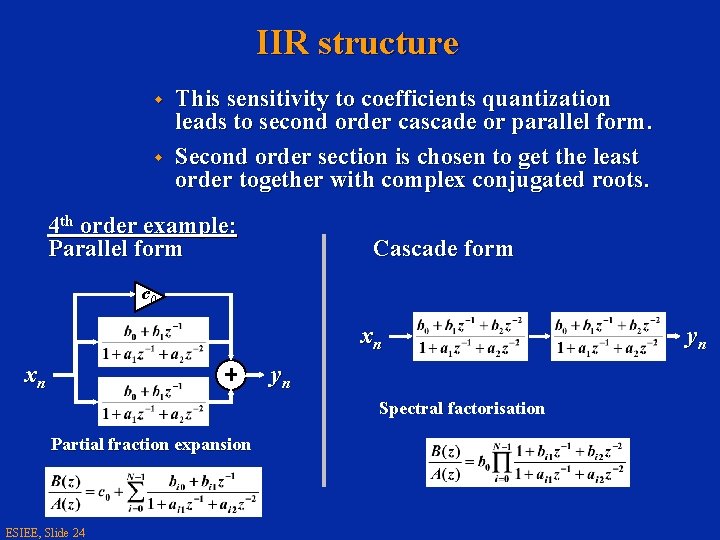
IIR structure w w This sensitivity to coefficients quantization leads to second order cascade or parallel form. Second order section is chosen to get the least order together with complex conjugated roots. 4 th order example: Parallel form Cascade form c 0 xn xn yn Spectral factorisation Partial fraction expansion ESIEE, Slide 24 yn

IIR – Cascade structure w Cascade structure involves addressing two problems : w w ESIEE, Slide 25 Pairing: which zeros with which poles to form a second order rational transfer function. The goal will be minimize the overshoot caused by the poles. Ordering: which second order section will be ahead and which one will be the last. To answer to this question we will have consider quantification noise and the way to minimize it.

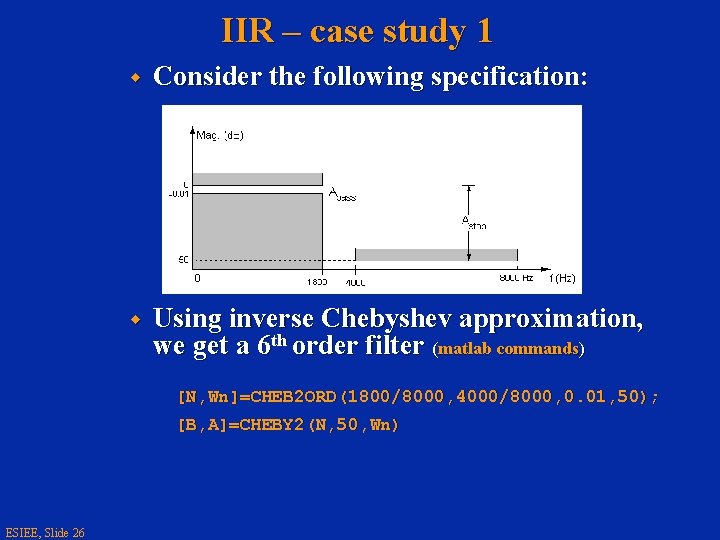
IIR – case study 1 w Consider the following specification: w Using inverse Chebyshev approximation, we get a 6 th order filter (matlab commands) [N, Wn]=CHEB 2 ORD(1800/8000, 4000/8000, 0. 01, 50); [B, A]=CHEBY 2(N, 50, Wn) ESIEE, Slide 26

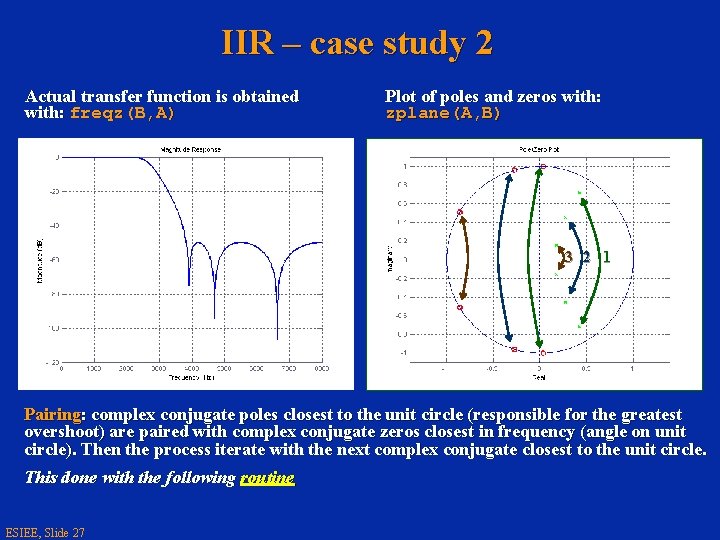
IIR – case study 2 Actual transfer function is obtained with: freqz(B, A) Plot of poles and zeros with: zplane(A, B) 3 2 1 Pairing: complex conjugate poles closest to the unit circle (responsible for the greatest overshoot) are paired with complex conjugate zeros closest in frequency (angle on unit circle). Then the process iterate with the next complex conjugate closest to the unit circle. This done with the following routine ESIEE, Slide 27

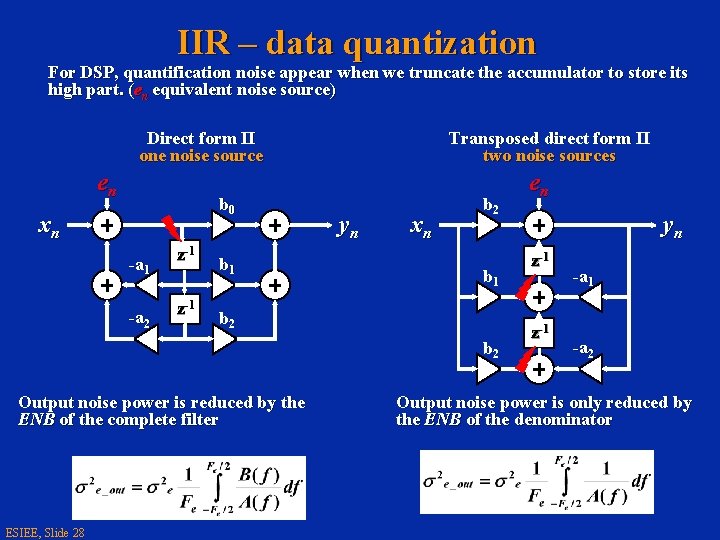
IIR – data quantization For DSP, quantification noise appear when we truncate the accumulator to store its high part. (en equivalent noise source) Direct form II one noise source en b 0 xn -a 1 -a 2 z-1 b 1 Transposed direct form II two noise sources yn xn b 2 b 1 b 2 Output noise power is reduced by the ENB of the complete filter ESIEE, Slide 28 en yn z-1 -a 2 Output noise power is only reduced by the ENB of the denominator

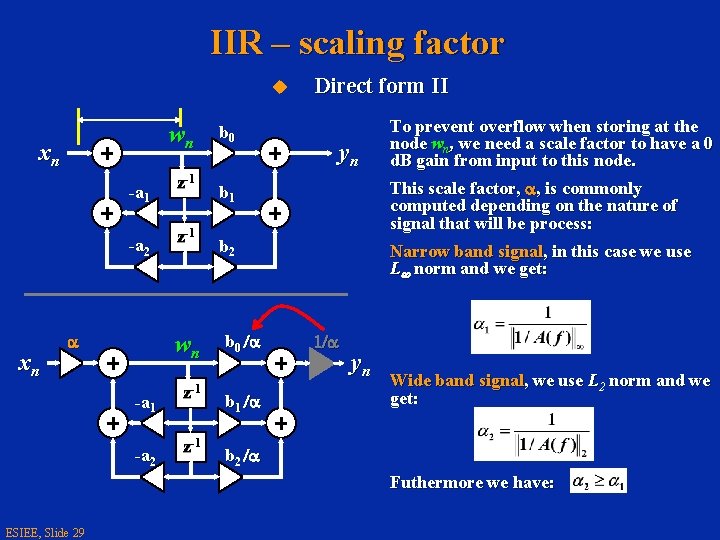
IIR – scaling factor u wn xn -a 1 -a 2 xn a z-1 wn -a 1 -a 2 b 0 Direct form II yn To prevent overflow when storing at the node wn, we need a scale factor to have a 0 d. B gain from input to this node. b 1 This scale factor, a, is commonly computed depending on the nature of signal that will be process: b 2 Narrow band signal, in this case we use L norm and we get: b 0 /a z-1 b 1 /a z-1 b 2 /a 1/a yn Wide band signal, we use L 2 norm and we get: Futhermore we have: ESIEE, Slide 29

IIR – ordering u Depend on: w w w Criteria for scale factor computation, L or L 2 norm. Which norm of the quantization noise we want to minimize L (max value) or L 2 norm (power). Following rules could apply: • L for scale factor and L 2 for noise • L 2 for scale factor and L for noise If the same norm is used ESIEE, Slide 30 ascending order of overshoot. descending order of overshoot. no prefered order.

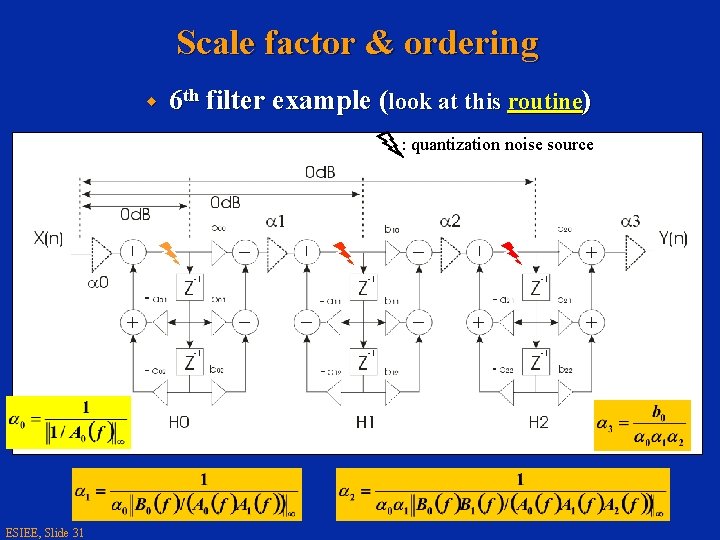
Scale factor & ordering w 6 th filter example (look at this routine) : quantization noise source ESIEE, Slide 31

IIR – coefficients coding w We have to choose the right Qn coding for the coefficients. w For second order section, A(z) or B(z) can be written, if we let their roots to be w Denominator: for stability we need |r|<1, so coefficients belong to [-2, 2]. Numerator, by using analog approximation function as prototype we get zeros on the unit circle so |r|=1 and coefficients also belong to [-2, 2]. w w The right coding is then Q 14 for 16 bits word. w ESIEE, Slide 32 Look at this routine which does the work fir the 6 th order filter.

IIR – noise power w The noise power at the output of that 6 th order filter: First stage noise power Second stage noise power Third stage noise power Input scale factor attenuates only the input signal not the quantization noise: • the lower the scale factor is the worst the signal to noise ratio will be. ESIEE, Slide 33

IIR - computation u Evaluation of an order 2 direct form II is as follows: ACC=x(n) a 0 Q 29=Q 15 Q 14 ACC=ACC - a 1 w(n-1) Q 29=Q 29 - (Q 15 Q 14) ACC=ACC - a 2 w(n-2) Q 29=Q 29 - (Q 15 Q 14) ACC<<2 Q 31=Q 29 22 w(n)=ACCH Q 15 ACC=w(n) b 0 Q 29=Q 15 Q 14 ACC=ACC + b 2 w(n-2) Q 29=Q 29 + (Q 15 Q 14) ACC=ACC + b 1 w(n-1) Q 29=Q 29 + (Q 15 Q 14) ACC<<2 Q 31=Q 29 22 y(n)=ACCH Q 15 w(n-2)=w(n-1)=w(n) ESIEE, Slide 34

IIR – program on C 54 w Following program works on a sample by sample basis and is C callable. Memory managment sect 1 a a 11 a 12 b 11 b 10 a 21 a 22 b 21 b 20 ESIEE, Slide 35 *AR 2 memfilt w 1(n-1) w 1(n-2) w 2(n-1) w 2(n-2) *AR 3

Follow on Activities for thr C 5416 DSK u Laboratory 6 for the C 5416 DSK w u Laboratory 7 for the C 5416 DSK w u Implemements band stop and notch filters using poles / zeroes and Bilinear Transform (BLT). Laboratory 8 for the C 5416 DSK w ESIEE, Slide 36 Implemements high pass and low pass Butterworth filters from 1 st order to 6 th order. Looks at sharpness of cut off and stability of IIR filters designed by placing poles and zeroes and Bilinear Transform (BLT).

Follow on Activities for thr C 5510 DSK u Application 3 for the C 5510 DSK w Uses IIR filter for reverberation w w ESIEE, Slide 37 Simulates single and multiple reflections from the walls of a room. Introduces the configuration used for an Infinite Impulse Response (IIR) filter. The majority of the code is written in C, except where the C code would be too slow and assembly code is required