DETERMINANTES Definio Determinante um nmero associado a uma

DETERMINANTES Definição: Determinante é um número associado a uma matriz quadrada de ordem n x n. Matriz quadrada de ordem 1 Se A é uma matriz quadrada de ordem 1, isto é A = ( a 11 ), o seu determinante será o próprio elemento a 11. det A = a 11 Exemplo. : A = ( 120 ) det A = 120 B = (– 29 ) det A = – 29 www. vestibular 1. com. br

Matriz quadrada de ordem 2 a 11 A= a 21 a 12 a 22 a 11 det A = a 21 a 12 = a 11 a 22 – a 12 a 21 a 22 Produto dos elementos da diagonal principal menos o produto da diagonal secundária. – 3 A= 1 2 – 5 – 3 det A = 1 2 = (– 3) (– 5) – (2) (1) – 5 det A = 15 – 2 = 13 det A = 13 www. vestibular 1. com. br

Matriz quadrada de ordem 3 Regra de Sarrus: Repete-se as duas primeiras linhas abaixo da terceira linha ou repete-se as duas primeiras colunas após a terceira coluna. Em seguida, calcula-se a soma do produto da diagonal principal com o produto das diagonais paralelas a ela (SDP). Faz-se o mesmo com a diagonal secundária e suas paralelas (SDS). Em seguida, faz-se a diferença desses valores obtidos com as diagonais. (det A = SDP – SDS) www. vestibular 1. com. br

a 11 a 21 a 31 a 11 a 21 a 12 a 22 a 32 a 12 a 22 a 13 a 23 a 33 a 13 a 23 ou a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 a 11 a 21 a 31 a 12 a 22 a 32 SDP = ( a 11 a 22 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23 ) SDS = ( a 13 a 22 a 31 + a 23 a 32 a 11 + a 33 a 12 a 21 ) det A = SDP – SDI www. vestibular 1. com. br

Propriedades dos determinantes 1. Um determinante será nulo quando possuir uma fila formada só por zeros ou duas filas paralelas iguais ou proporcionais 0 det A = 3 1 0 = (0) (5) – (0) (3) = 0 – 0 = 0 5 3 5 0 – 5 3 5 det A = ( 0 + 45 – 15 ) – ( 0 + 45 – 15 ) det A = 0 www. vestibular 1. com. br

2. Se trocarmos entre si a posição de duas filas paralelas, o determinante mudará o sinal. 1 3 5 det A = 3 0 – 5 2 1 2 det A = ( 0 + 15 – 30 ) – ( 0 – 5 + 18 ) det A = (– 15 ) – ( 13 ) det A = – 28 2 det A = 3 1 1 2 0 – 5 = ( 0 + 18 – 5 ) – ( 0 – 30 + 15 ) 3 5 ( 13 ) – ( – 15 ) det A = 28 www. vestibular 1. com. br

3. Se multiplicarmos umas das filas de uma matriz quadrada por um número k, o seu determinante ficará multiplicado por k. 2 4 det A = = (10) – (12) = – 2 3 5 k=3 6 det B = 3 12 = (30) – (36) = – 6 5 det B = k det A det B = 3 (– 2) = – 6 www. vestibular 1. com. br

4. Da propriedade 3, decorre que: det ( k An ) = kn det An. 2 A 2 = 3 4 5 6 3 A 2 = 9 12 15 k=3 6 det ( 3 A 2) = 9 12 = (90) – (108) = – 18 15 det ( 3 A 2 ) = 32 det A 2 = 9 (– 2) = – 18 www. vestibular 1. com. br

5. det A = det AT. 1 3 5 det A = 3 0 – 5 2 1 2 det A = ( 0 + 15 – 30 ) – ( 0 – 5 + 18 ) det A = (– 15 ) – ( 13 ) det A = – 28 1 det AT = 3 5 3 0 – 5 2 1 2 det AT = ( 0 – 30 + 15 ) – ( 0 – 5 + 18 ) det AT = (– 15 ) – ( 13 ) det AT = – 28 www. vestibular 1. com. br

6. det ( An Bn ) = det A det B 2 A 2 = 3 4 5 2 A 2 B 2 = 3 3 ; B 2 = 1 4 3 5 1 10 2 10 10 = 2 14 28 40 det ( An Bn ) = 400 – 392 = 8 det A det B = (– 2) (– 4) = 8 www. vestibular 1. com. br

7. det In = 1 1 det I 3 = 0 0 0 1 det I 3 = 1 8. O determinante de matrizes triangulares e de matrizes diagonais se resume ao produto dos elementos da diagonal principal. 5 det A = 0 0 3 – 2 0 2 1 3 det A = 5 (– 2) 3 = – 30 www. vestibular 1. com. br

Matriz inversa Seja A uma matriz quadrada de ordem n. Essa matriz possuirá inversa (A– 1) se, e somente se, seu determinante for diferente de zero. A– 1 A = A A– 1 = I det A 0. 1. Se A 2 x 2 = 2. det A– 1 = a b c d , então : A– 1 = d det A –c det A –b det A a det A 1 , det A 0 det A 3. Se A possuir inversa, essa será única. www. vestibular 1. com. br

01. (Fuvest – SP) Se a é uma matriz 2 x 2 iversível que satisfaz A 2 = 2 A, então o determinante de A será: a) 0. 2 = det (2 A) det A b) 1. c) 2. det A = 22 det A d) 3. e) 4. det A = 4 E www. vestibular 1. com. br

02. (Udesc) O grau do polinômio que expressa o x determinante da matriz A = 2 1 a) 3. b) 2. c) 1. d) 0. e) 4. x P(x) = 2 1 x 2 x 1 x –x x 1 2 + 2 x – x 2 – x + x 3 – 2 x P(x) = x x –x x 1 P(x) = x 3 – x x 1 Grau 3 x –x A www. vestibular 1. com. br

03. (UFSC) Assinale a(s) proposição(ões) correta(s). (01) Se K = (kij) é uma matriz quadrada de ordem 2 dada por kij = 22 i + j para i < j e kij = i 2 + 1 para i > j, então k é uma matriz inversível. k 11 K= k 21 k 12 k 22 k 11 = 12 + 1 = 2 k 12 = 22(1) + 2 = 24 = 16 k 21 = 22 + 1 = 5 k 22 = 22 + 1 = 5 2 K= 5 16 5 Det K = 10 – 80 = – 70 0 é inversível (01) - correta www. vestibular 1. com. br

(02) Se A e B são matrizes tais que A B é uma matriz nula, então A é uma matriz nula ou B é uma matriz nula. A B = 0 não implica em A = 0 ou B = 0. (02) - incorreta (04) Sejam as matrizes M e P, respectivamente de tipos 5 x 7 e 7 x 5. Se R = MP, então a matriz R 2 tem 625 elementos. Ordem n M 5 x 7 P 7 x 5 = R 5 x 5 (A matriz R possui 25 elementos) c. e. p Logo, a matriz R 2 tem 25 elementos. (04) - incorreta www. vestibular 1. com. br

(08) Chamamos de “traço de L” e anotamos Tr(L) a soma do elementos da diagonal principal de uma matriz quadrada L; então Tr(L) = Tr(LT). A transposta de uma matriz não altera sua diagonal principal. (08) - correta GABARITO QUESTÃO 03 : 01 + 08 = 09 www. vestibular 1. com. br

SISTEMAS LINEARES Equação Linear é uma equação de forma: a 1 x 1 + a 2 x 2 + a 3 x 3 +. . . + an xn = b Portanto, um sistema será linear quando for composto de equações lineares. 2 x + 3 y = 5 x–y=2 2 x 2 + 3 y = 5 x–y=2 linear não-linear 2 x + 3 y – z = 5 x–y +z=2 – 5 x – 3 y + 4 z = 10 2 xy + 3 y = 5 x–y=2 www. vestibular 1. com. br

Observações: 1. 3 x + 2 y + z = 1 x – y + 3 z = 2 5 x + 2 y + z = 7 3 2 1 1 – 1 3. 5 2 1 x y = z 1 2 7 Forma matricial 3 2 1 1 Forma matricial 1 – 1 3 2 completa 5 2 1 7 2. A matriz constituída apenas pelos coeficientes é denominanda matriz principal. www. vestibular 1. com. br

3. Se o número de equações é igual ao número de variáveis e o determinante da matriz principal ( ) for diferente de zero, o sistema recebe o nome de normal. 4. Se todos os termos independentes são nulos (0), o sistem é chamado de homogêneo. 2 x + 3 y = 0 x–y=0 www. vestibular 1. com. br

Método de Cramer a 11 x 1 + a 12 x 2 + a 13 x 3 +. . . + a 1 n xn = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 +. . . + a 2 n xn = b 2. . . an 1 x 1 + an 2 x 2 + an 3 x 3 +. . . + ann xn = bn a 11 = a. . 21. an 1 a 12 a 13 a 22 a 23. . . an 2 an 3 . . . a 1 n a 2 n . . . ann www. vestibular 1. com. br

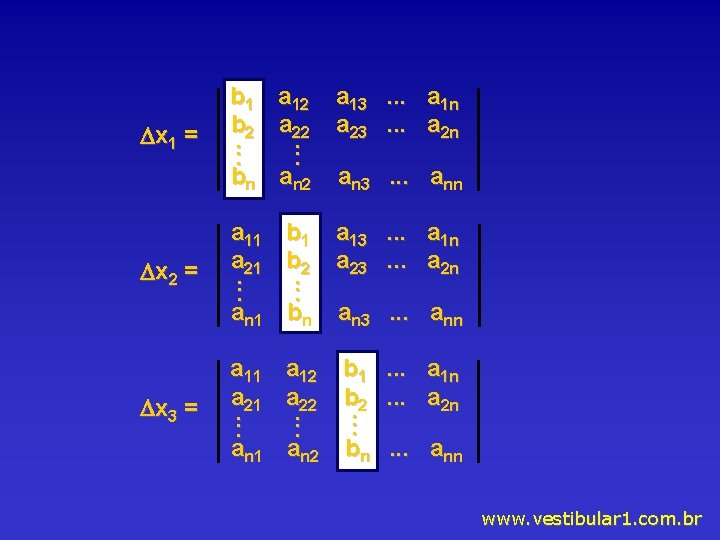
x 1 = x 2 = x 3 = b 1 a 12 a 13 b 2 a 23. . . bn an 2 an 3 . . . a 1 n. . . a 2 n a 11 b 1 a 13 a 21 b 2 a 23. . . an 1 bn an 3 . . . a 1 n. . . a 2 n a 11 a 12 b 1 a 22 b 2. . an 1 an 2 bn . . . a 1 n. . . a 2 n . . . ann www. vestibular 1. com. br

xn = a 11 a 12 a 13 a 21 a 22 a 23. . . an 1 an 2 an 3 . . . b 1. . . b. 2. . . bn Se 0 temos: x 1 x 2 x 3 xn x 1 = , x 2 = , x 3 = , . . . , xn = www. vestibular 1. com. br

Exemplo: 3 x + 2 y = 8 x–y=1 3 2 = =– 3– 2=– 5 1 -1 x = 8 2 = – 8 – 2 = – 10 1 -1 y = 3 1 8 =3– 8=– 5 1 x x = = – 10 – 5 = 2 y y = = – 5 = 1 S = {(x, y)} S = {(2, 1)} www. vestibular 1. com. br

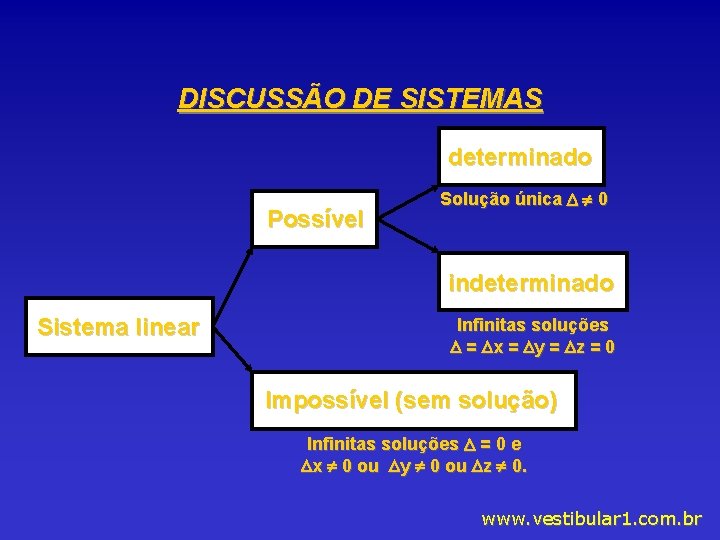
DISCUSSÃO DE SISTEMAS determinado Possível Solução única 0 indeterminado Sistema linear Infinitas soluções = x = y = z = 0 Impossível (sem solução) Infinitas soluções = 0 e x 0 ou y 0 ou z 0. www. vestibular 1. com. br

Se o sistema linear for homogêneo: Possível e determinado ( 0 , S = {(0, 0, 0, . . . , 0)} ) Solução trivial Possível e indeterminado ( = 0 ) (Além da trivial, admitirá soluções próprias) www. vestibular 1. com. br

04. Três amigos sobem em uma balança de dois em dois. Antônio e Beatriz somam 30 kg e Beatriz e Caio, 28 kg. Sabe-se que Antônio e Caio pesam juntos 34 kg. Quanto pesa Beatriz? A+B = 30 B + C = 28 A + C = 34 (–) A + B = 30 + -A + B = – 6 2 B = 24 B = 12 Beatriz tem 12 kg. www. vestibular 1. com. br

x+y+z=1 05. (UFSM – RS) Considere o sistema 2 x + 2 y + 2 z = m. 3 x + 3 y + 3 z = 4 Então, pode-se afirmar que o sistema é: a) possível e indeterminado. b) Impossível para qualquer valor de m. c) Possível e determinado. d) Possível para m 2. e) Impossível apenas quando m 2. www. vestibular 1. com. br

x+y+z=1 2 x + 2 y + 2 z = m 3 x + 3 y + 3 z = 4 x+y+z=1 m x+y+z= 2 4 x+y+z= 3 (2) (3) x+y+z=1 4 x+y+z= 3 Impossível para qualquer valor de m. B www. vestibular 1. com. br

Acesse as nossas páginas e confira uma infinidade de simulados de Matemática e de outras matérias! www. vestibular 1. com. br Vestibular 1 – O Número 1 em vestibulares! A melhor ajuda ao vestibulando na Internet e em todo o Brasil. O Portal que mais aprova! Confira! Apoio total aos vestibulandos! Autor desta Aula: ANALBERTO SCHOT - professor BELL. Criciúma - SC www. vestibular 1. com. br