MATEMTICA DETERMINANTES DETERMINANTES 1 DEFINIO SENDO M O

DETERMINANTES: 1) DEFINIÇÃO SENDO M O CONJUNTO DAS MATRIZES QUADRADAS E R O CONJUNTO

DETERMINANTES: a) Se n = 1 det Mn = a 11 b) Se n

DETERMINANTES: 2) Regras Práticas § Determinante de 2ª ordem a 11 a 12 a

DETERMINANTES: § DETERMINANTE DE 3ª ORDEM (REGRA DE SARRUS) - a 11 a 12

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO a) UMA FILA NULA 1 0 -1

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO b) DUAS FILAS PARALELAS IGUAIS 1 1

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO c) DUAS FILAS PARALELAS PROPORCIONAIS 1 3

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO d) UMA FILA É COMBINAÇÃO LINEAR DE

DETERMINANTES: ALTERAÇÕES NO DETERMINANTE a) TROCANDO A POSIÇÃO DE DUAS FILAS PARALELAS , O

DETERMINANTES: ALTERAÇÕES NO DETERMINANTE b) MULTIPLICANDO UMA FILA POR , O DETERMINANTE FICA MULTIPLICADO

DETERMINANTES: c) UM DETERMINANTE FICA MULTIPLICADO POR , QUANDO TODO OS ELEMENTOS DO DETERMINANTE

DETERMINANTES: DETERMINANTE NÃO SE ALTERA a) SE TROCAR EM ORDEM LINHAS POR COLUNAS 2

DETERMINANTES: TEOREMA DE BINET SE A E B SÃO MATRIZES QUADRADOS DE MESMA ORDEM,

Slides: 14

Download presentation

MATEMÁTICA DETERMINANTES

DETERMINANTES: 1) DEFINIÇÃO SENDO M O CONJUNTO DAS MATRIZES QUADRADAS E R O CONJUNTO DOS REAIS, ENTÃO: “DETERMINE A FUNÇÃO det: M R, ONDE Mn det Mn, TAL QUE:

DETERMINANTES: a) Se n = 1 det Mn = a 11 b) Se n = 2 det Mn = a 11 a 12 a 21 a 22 c) Se n = 3 det Mn = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

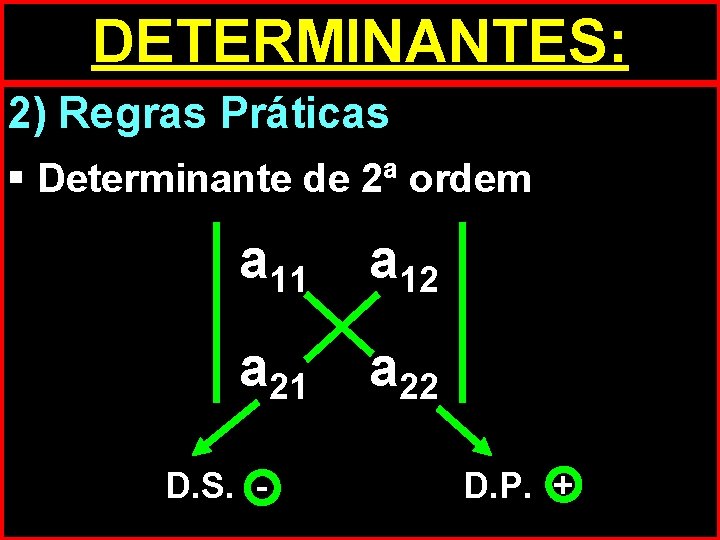
DETERMINANTES: 2) Regras Práticas § Determinante de 2ª ordem a 11 a 12 a 21 a 22 D. S. - D. P. +

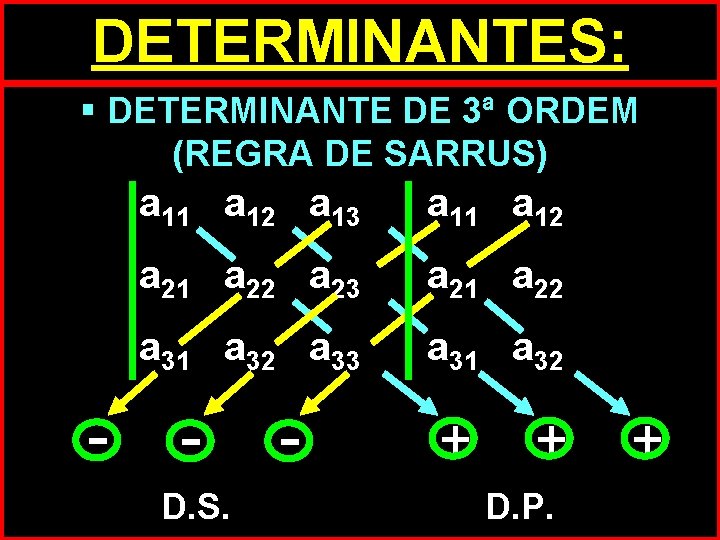
DETERMINANTES: § DETERMINANTE DE 3ª ORDEM (REGRA DE SARRUS) - a 11 a 12 a 13 a 11 a 12 a 21 a 22 a 23 a 21 a 22 a 31 a 32 a 33 a 31 a 32 D. S. - + + D. P. +

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO a) UMA FILA NULA 1 0 -1 4 0 9 = 0 OU 3 0 5 5 1 2 9 3 2 =0 0

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO b) DUAS FILAS PARALELAS IGUAIS 1 1 5 4 4 7 =0 3 3 2 C 1 = C 2 OU 1 4 3 6 7 2 =0 1 4 3 L 1 = L 3

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO c) DUAS FILAS PARALELAS PROPORCIONAIS 1 3 1 4 12 5 = 0 3 9 2 C 2 = 3 C 1 0 2 -1 OU 6 4 2 = 0 0 4 -2 L 1 = 2 L 3

DETERMINANTES: 3) PROPRIEDADES DETERMINANTE IGUAL A ZERO d) UMA FILA É COMBINAÇÃO LINEAR DE DUAS FILAS PARALELAS 1 4 3 2 4 5 =0 -1 0 -2 L 1 = L 2 + L 3 4 0 4 OU -1 2 -3 = 0 3 9 -6 C 3 = C 1 – C 2

DETERMINANTES: ALTERAÇÕES NO DETERMINANTE a) TROCANDO A POSIÇÃO DE DUAS FILAS PARALELAS , O DETERMINANTE TROCA DE SINAL 2 0 1 -2 2 1 = -6 1 4 3 0 2 1 2 -2 1 = 6 4 1 3

DETERMINANTES: ALTERAÇÕES NO DETERMINANTE b) MULTIPLICANDO UMA FILA POR , O DETERMINANTE FICA MULTIPLICADO POR . 2 0 1 -2 2 1 1 4 3 (x 2) = -6 4 0 1 -4 2 1 2 4 3 = 2. (-6)= -12

DETERMINANTES: c) UM DETERMINANTE FICA MULTIPLICADO POR , QUANDO TODO OS ELEMENTOS DO DETERMINANTE FOREM MULTIPLICADOS POR Ex: 1) . 1 3 2 0 -2 1 = 5 2 1 4 SE MULTIPLICARMOS TODOS OS ELEMENTOS POR 2 2 6 4 0 -4 2 , então seu resultado será 3. (5) = 40 2 4 2 8 2) Se M é matriz de 3ª ordem e det(m) = 8, então det(3 m) = 33. det(m) = 27. 8 = 216

DETERMINANTES: DETERMINANTE NÃO SE ALTERA a) SE TROCAR EM ORDEM LINHAS POR COLUNAS 2 1 4 0 9 3 6 7 8 = 2 0 6 1 9 7 4 3 8 b) SE SOMARMOS A UMA FILA UMA COMBINAÇÃO LINEAR DE OUTRAS FILAS PARALELAS (TEOREMA DE JACOBI) 2 1 3 6 4 2 7 0 7 = 2 1 0 6 4 8 7 0 0 C 3 = C 1 + C 2 – C 3

DETERMINANTES: TEOREMA DE BINET SE A E B SÃO MATRIZES QUADRADOS DE MESMA ORDEM, ENTÃO : det (A. B) = det(A). det(B) Ex: 1 2 4 det -1 5 3 0 1 2 . 1 -1 0 2 0 1 4 3 1 = det 1 2 4 1 -1 0 -1 5 3. det 2 0 1 2 4 3 1