Cryptography Lecture 7 Pseudorandom functions Keyed functions Let

Cryptography Lecture 7

Pseudorandom functions

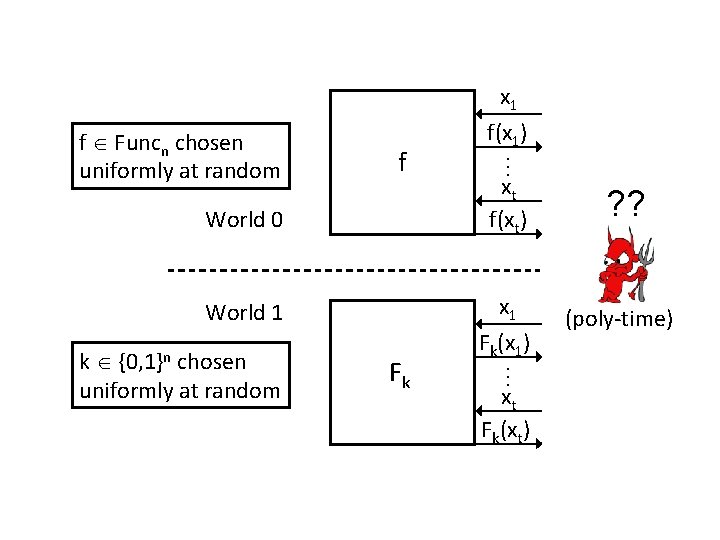
Keyed functions • Let F: {0, 1}* x {0, 1}* be an efficient, deterministic algorithm – Define Fk(x) = F(k, x) – The first input is called the key • Assume F is length preserving: F(k, x) only defined if |k|=|x|, in which case |F(k, x)| = |k| = |x| • Choosing a uniform k {0, 1}n is equivalent to choosing the function Fk : {0, 1}n – I. e. , for fixed key length n, the algorithm F defines a distribution over functions in Funcn!

World 0 World 1 k {0, 1}n chosen uniformly at random Fk … f xt f(xt) ? ? x 1 Fk(x 1) (poly-time) … f Funcn chosen uniformly at random x 1 f(x 1) xt Fk(xt)

Pseudorandom permutations (PRPs) • Let f Funcn • f is a permutation if it is a bijection – This means that the inverse f-1 exists • Let Permn Funcn be the set of permutations • What is |Permn|?

Pseudorandom permutations • Let F be a length-preserving, keyed function • F is a keyed permutation if – Fk is a permutation for every k – Fk-1 is efficiently computable (where Fk-1(Fk(x)) = x) • F is a pseudorandom permutation if Fk , for uniform key k {0, 1}n, is indistinguishable from a uniform permutation f Permn

Note • For large enough n, a random permutation is indistinguishable from a random function • So in practice, PRPs are also good PRFs • Proof in the book (required!)

PRFs vs. PRGs • PRF F immediately implies a PRG G: – Define G(k) = Fk(0… 0) | Fk(0… 1) – I. e. , G(k) = Fk(<0>) | Fk(<1>) | Fk(<2>) | …, where <i> denotes the n-bit encoding of i • PRF can be viewed as a PRG with random access to exponentially long output – The function Fk can be viewed as the n 2 n-bit string Fk(0… 0) | … | Fk(1… 1)

Do PRFs/PRPs exist? • They are a stronger primitive than PRGs… – …though can be built from PRGs • In practice, block ciphers are used

Block ciphers • Block ciphers are practical constructions of pseudorandom permutations • No asymptotics: F: {0, 1}n x {0, 1}m – n = “key length” – m = “block length” • Hard to distinguish Fk from uniform f Permm even for attackers running in time 2 n

AES • Advanced encryption standard (AES) – Standardized by NIST in 2000 based on a public, worldwide competition lasting over 3 years – Block length = 128 bits – Key length = 128, 192, or 256 bits • Will not discuss details later in the course • No real reason to use anything else

CPA-security • Fix , A • Define a randomized exp’t Priv. KCPAA, (n): 1. k Gen(1 n) 2. A(1 n) interacts with an encryption oracle Enck(·), and then outputs m 0, m 1 of the same length 3. b {0, 1}, c Enck(mb), give c to A 4. A can continue to interact with Enck(·) 5. A outputs b’; A succeeds if b = b’, and experiment evaluates to 1 in this case

CPA-security • is secure against chosen-plaintext attacks (CPA-secure) if for all PPT attackers A, there is a negligible function such that Pr[Priv. KCPAA, (n) = 1] ≤ ½ + (n)

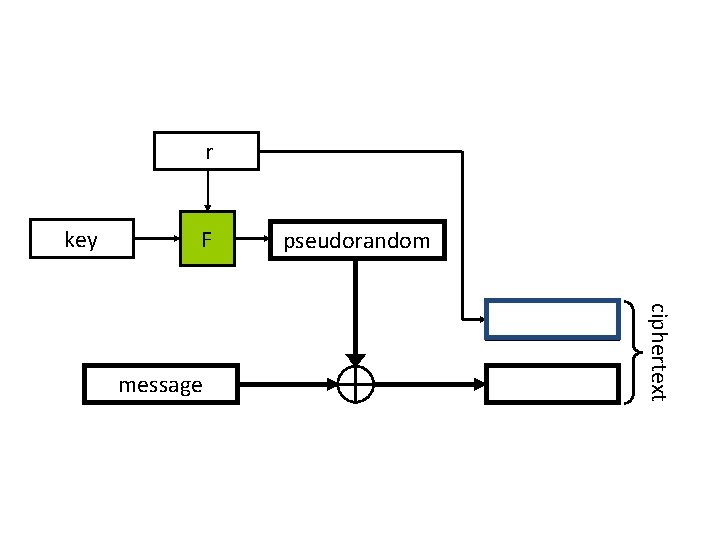
CPA-secure encryption • Let F be a length-preserving, keyed function • Gen(1 n): choose a uniform key k {0, 1}n • Enck(m), for |m| = |k|: – Choose uniform r {0, 1}n (nonce/initialization vector) – Output ciphertext < r, Fk(r) m > • Deck(c 1, c 2): output c 2 Fk(c 1) • Correctness is immediate

r key F ciphertext message pseudorandom

Security? • Theorem: if F is a pseudorandom function, then this scheme is CPA-secure

Note • The key may be as long as the message… • …but the same key can be used to safely encrypt multiple messages

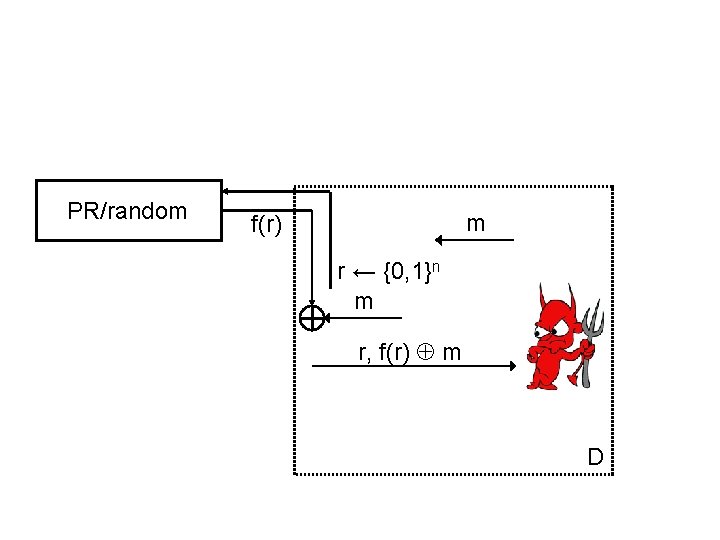
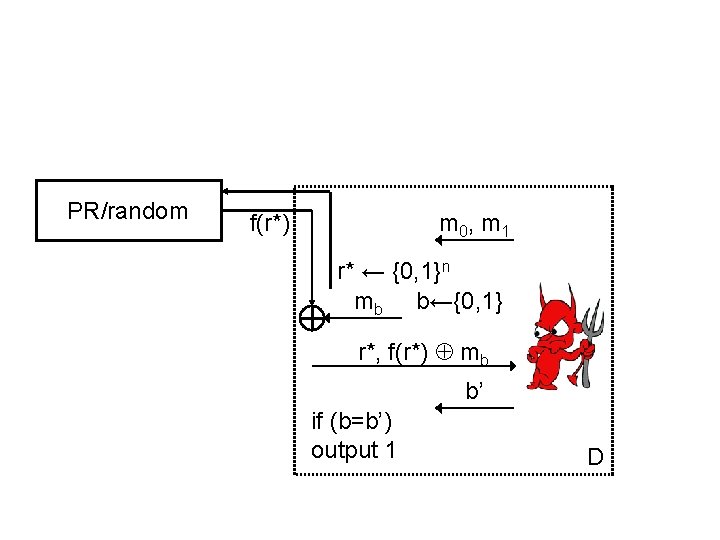
Security? • Theorem: if F is a pseudorandom function, then this scheme is CPA-secure • Proof by reduction… • Let denote the scheme

PR/random m f(r) r ← {0, 1}n m r, f(r) m D

PR/random m 0 , m 1 f(r*) r* ← {0, 1}n mb b←{0, 1} r*, f(r*) mb b’ if (b=b’) output 1 D

Analysis • Let µ(n) = Pr[Priv. CPAAdv, Π(n) = 1] • Let q(n) be a bound on the number of encryption queries made by attacker • If f = Fk for uniform k, then the view of Adv is exactly as in Priv. CPAAdv, Π(n) Prk {0, 1}n[DFk(·) =1] = Pr[Priv. CPAAdv, Π(n) = 1] = µ(n)

Analysis • If f is uniform, there are two sub-cases – r* was used for some other ciphertext (call this event Repeat) – r* was not used for some other ciphertext • Prf[Df(·) =1] ≤ Prf[Df(·) =1| Repeat] + Pr[Repeat] – Pr[Repeat] ≤ q(n)/2 n – Prf[Df(·) =1 | Repeat] = ½

Analysis • Since F is pseudorandom… | µ(n) – Prf[Df(·) =1] | ≤ ε(n) µ(n) ≤ Prf[Df(·) =1] + ε(n) ≤ ½ + q(n)/2 n + ε(n) • For any polynomial q, the term q(n)/2 n is negligible Pr[Priv. CPAAdv, Π(n) = 1] = µ(n) ≤ ½ + ε’(n) QED

Real-world security? • The security bound we proved is tight • What happens if a nonce r is ever reused? • What is the probability that the nonce used in some challenge ciphertext is also used for some other ciphertext? • What happens to the bound if the nonce is chosen non-uniformly?

CPA-secure encryption • We have shown a CPA-secure encryption scheme based on any block cipher/PRF – Enck(m) = <r, Fk(r) m> • Drawbacks? – A 1 -block plaintext results in a 2 -block ciphertext – Only defined for encryption of n-bit messages

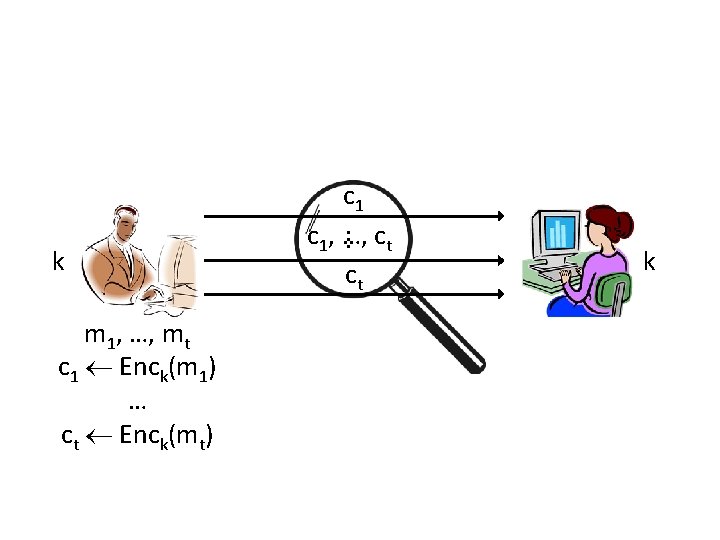
Encrypting long messages? • Recall that CPA-security for the encryption of multiple messages • So, can encrypt the message m 1, …, mt as Enck(m 1), Enck(m 2), …, Enck(mt) – This is also CPA-secure!

m 1, …, mt c 1 Enck(m 1) … ct Enck(mt) . . . k c 1, …, ct ct k

Drawback • The ciphertext is twice the length of the plaintext – I. e. , ciphertext expansion by a factor of two • Can we do better? • Modes of operation – Block-cipher modes of operation – Stream-cipher modes of operation

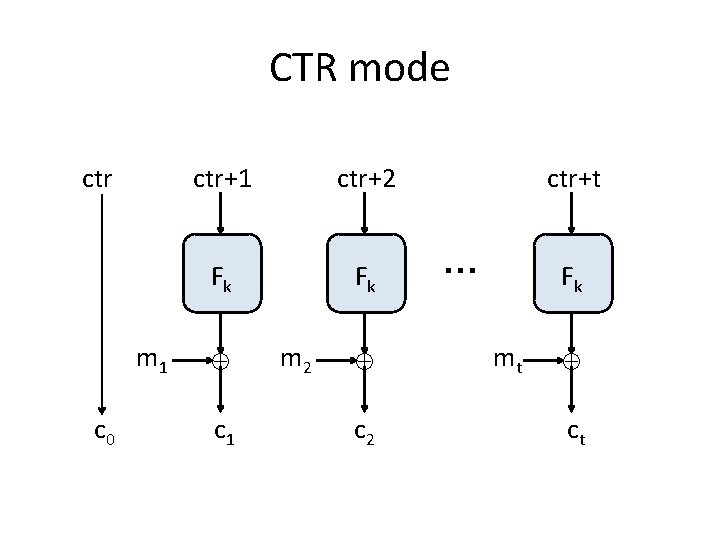
CTR mode • Enck(m 1, …, mt) // note: t is arbitrary – Choose ctr {0, 1}n, set c 0 = ctr – For i=1 to t: • ci = mi Fk(ctr + i) – Output c 0, c 1, …, ct • Decryption? • Ciphertext expansion is just 1 block

CTR mode ctr m 1 c 0 ctr+1 ctr+2 Fk Fk c 1 m 2 ctr+t … Fk mt ct

CTR mode • Theorem: If F is a pseudorandom function, then CTR mode is CPA-secure • Proof sketch: The sequence Fk(ctri + 1), …, Fk(ctri + t) used to encrypt the ith message is pseudorandom – Moreover, it is independent of every other such sequence unless ctri + j = ctri’ + j’ for some i, j, i’, j’ • Just need to bound the probability of that event

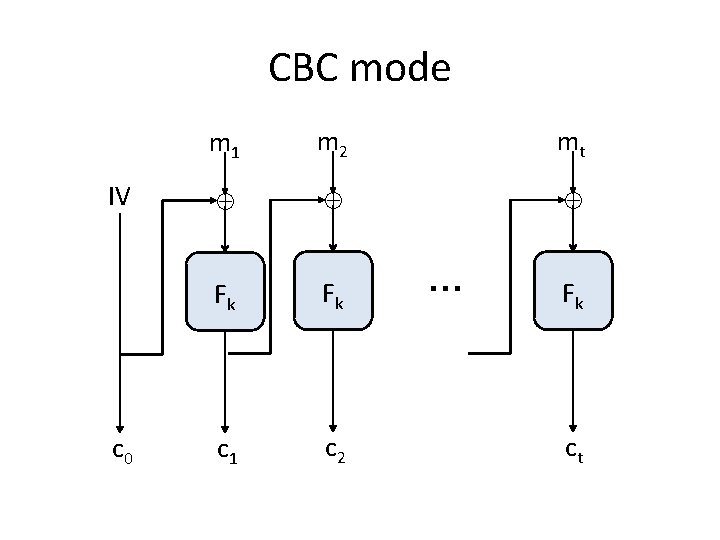
CBC mode • Enck(m 1, …, mt) // note: t is arbitrary – Choose random c 0 {0, 1}n (also called the IV) – For i=1 to t: • ci = Fk(mi ci-1) – Output c 0, c 1, …, ct • Decryption? – Requires F to be invertible • Ciphertext expansion is just 1 block

CBC mode IV c 0 m 1 m 2 mt Fk Fk c 1 c 2 … Fk ct

CBC mode • Theorem: If F is a pseudorandom permutation, then CBC mode is CPA-secure • Proof is more complicated than for CTR mode

ECB mode • Enck(m 1, …, mt) = Fk(m 1), …, Fk(mt) • Deterministic – Not CPA-secure! • Can tell from the ciphertext whether mi = mj – Not even EAV-secure!

Not just a theoretical problem! original encrypted using ECB mode (Taken from http: //en. wikipedia. org and derived from images created by Larry Ewing (lewing@isc. tamu. edu) using The GIMP. )