Network Security Prof N N GAIKWAD M P

Network Security Prof. N. N. GAIKWAD M. P. A. S. C COLLEGE PANVEL DIST-RAIGAD

ONE TIME PAD/ VERNAM CIPHER Is perfect secrecy possible? If each PT symbol encrypted with a randomly chosen key (Shannon) This idea used by Vernam to create One time pad Key has same length as the PT and key chosen randomly Known as Perfect Cipher Attacks impossible for sufficiently long PT msgs

ONE TIME PAD/ VERNAM CIPHER Generally not usable in practice Key is random & as long as the PT msg Can be used to store some secret data in a public computer Scenario: President of a country needs to send a secret msg to president of another country Send a trusted envoy with the random key b 4 sending the msg

ROTOR CIPHER Basic idea: mono aphabetic substitution, but each time the (PT char to CT char) mapping is changed

ROTOR CIPHER Initial position = Secret Key The first PT char is encrypted with the initial setting, the second with the setting after first rotation, and so on. . If the rotor is stationary then ? ? Encrypt ”bee” with the given key

TRANSPOSITION CIPHERS Change location of the symbols in PT to get CT An ”a” at the first position of the PT may appear at the tenth position in CT Does permutation of characters

Keyless transposition ciphers RAIL FENCE CIPHER Consider the PT msg ”Meet me at the park” CT msg = ”MEMATEAKETETHPR” Cryptanalysis very easy => 2 rows only & no key

Keyless transposition ciphers Another method PT = row by row CT = col by col Cryptanalysis Easy if attacker knows number of cols.

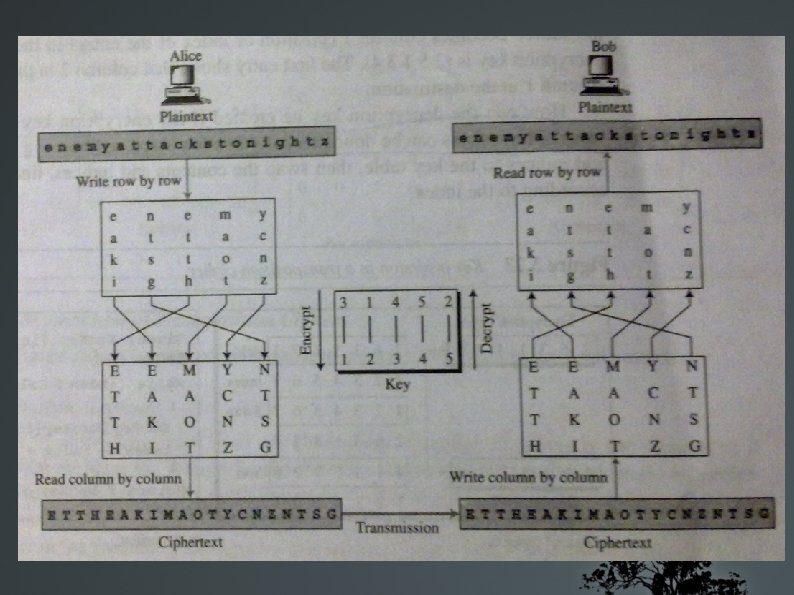
Keyed transposition ciphers Idea : divide PT chars into groups of predetermined size called 'blocks' and use a permutation key Eg: - Consider ”enemy attacks tonight” Group chars into blocks of size 5 (an agreed-upon value by both Alice and Bob) Use a bogus char (say z) to ”fill” the last block Result: enemy attac kston ightz

Keyed transposition ciphers Permutation key Encryption 3 1 4 1 2 3 5 4 2 5 Cipher text EEMYN TAACT TKONS HITZG Decryption

Combining keyed & keyless Better scrambling Encryption & Decryption done in 3 steps PT msg written into a table row by row Permutation done by reordering cols (based on key) The new table read col by col ( ==> CT msg )

Combining keyed & keyless

Combining keyed & keyless Keys Table is not necessary Eg: enc key : 3 1 4 5 2 & dec key: 2 5 1 3 4 Finding Enc/Dec key from the other Write index below Swap values with indices Sort values in ascending order of index Try for: 2 6 3 1 4 7 5

Combining keyed & keyless Key as a matrix

Combining keyed & keyless Cryptanalysis Trans. Ciphers don't change the frequency of chars But frequency of digrams & trigrams hidden Brute force attack extremely difficult

Double transposition cipher

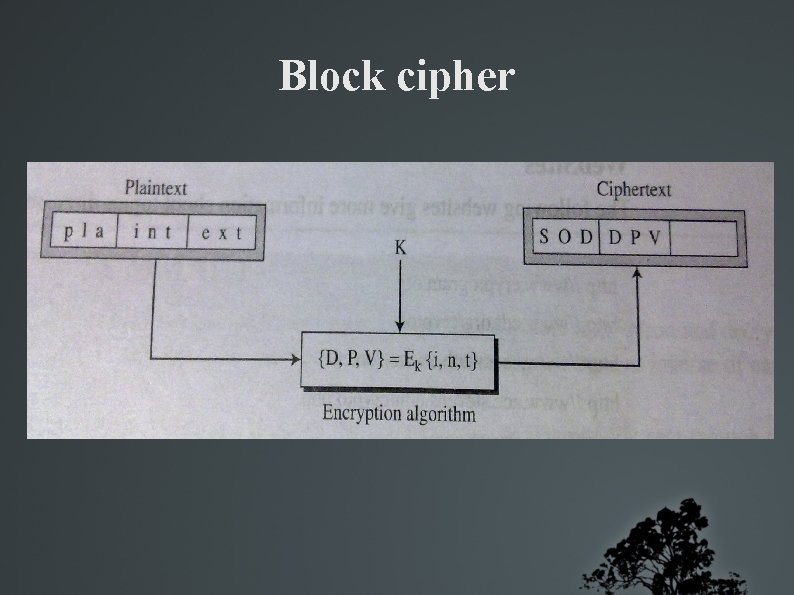
STREAM & BLOCK CIPHERS Literature divides symmetric ciphers into two broad categories – stream ciphers and block ciphers Stream cipher – encryption and decryption done symbol at a time Block ciphers – enc and dec done on a bolck of symbos at a time

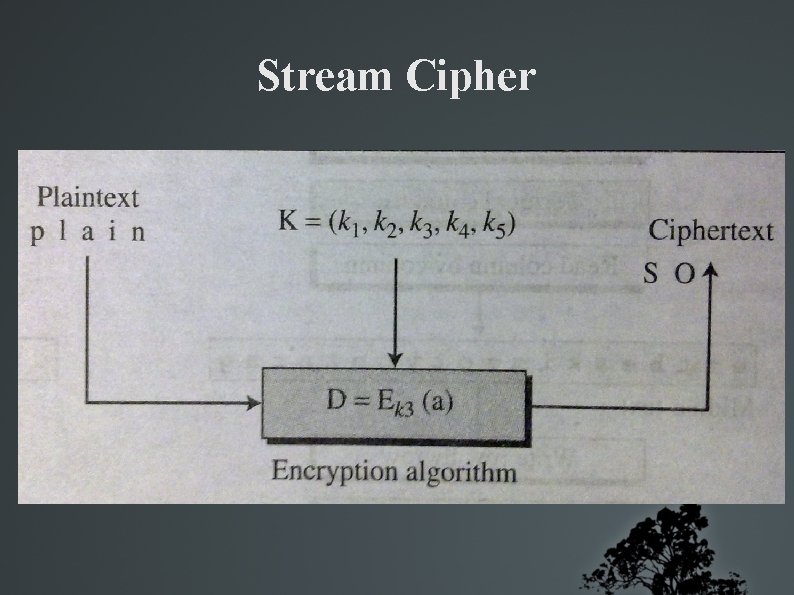
Stream Cipher There is a plain text stream There is a cipher text stream P = P 1 P 2 P 3. . . C = C 1 C 2 C 3. . . There is a key stream K = (k 1, k 2, k 3, . . . )

Stream Cipher

Stream cipher Examples Additive cipher Monoalphabetic substitution cipher K = (k, k, k, . . . ) K = mapping of the current PT char to CT char, . . . Vigenere cipher K = (k 1, k 2, . . . , km, k 1, k 2, . . . )

Block cipher

Block cipher Examples Play fair cipher (block size = 2) Hill cipher

Stream & Block Combined Idea: Blocks of PT encrypted individually Use a stream of keys to encrypt blocks (separate key for each block) Cipher is a block cipher when looking at the individual blocks Cipher is a stream cipher when looking at the whole msg considering each block as a single unit

Thank You