Modern Cryptography New Directions in Cryptography W Diffie

Modern Cryptography New Directions in Cryptography W. Diffie & M. E. Hellman Probabilistic Encryption S. Goldwasser & S. Micali

By 1976. . . Practically – Computers and “Private key security” exist (DES), and are becoming more and more applicable. Theoretically – Perfect secrecy [Shannon]. NOT MUCH BESIDES… The notion of a function easy to compute but hard to “inverse” arose. . . [Purdy] Complexity: NP (completeness) vs. P [Cook, Karp].

By 1976. . . (hush!) In fact, computers and cryptography go hand in hand from the first computers. (WWII) In fact, there were confidential papers in cryptography (in CESG): n. Non-secret-encryption [J. H. Ellis ‘ 70] (with a proof!) n¼RSA [C. C. Cocks ’ 73]

By 1976. . . (biographical details) In 1972, Whitfiled Diffie, an AI graduate student, developes more than an interest in cryptography. In 1974, at the age of 30, he phones Martin Hellman, assistant professor in Stanford, to discuss issues in crypto. They begin collaborating. In 1975, Diffie thinks of quitting altogether. "I was worried that I wasn't particularly remarkable as a programmer and that my lot in life would get progressively worse if things continued going as they were. " Also In 1975, he bares success. "The thing I remember distinctly is that I was sitting in the living room when I thought of it the first time and then I went downstairs to get a Coke and I almost lost it, " he says. "I mean, there was this moment when - I was thinking about something. What was it? And then I got it back and didn't forget it. "

New Directions in Cryptography W. Diffie & M. E. Hellman Diffie “We stand today on the brink of a revolution in cryptography”

Emphasis This is an invited paper, so: 1. NO definitions, notations, claims, proofs etc. 2. HOWEVER: clever ideas, clever insights! 3. Practicality. Historical survey.

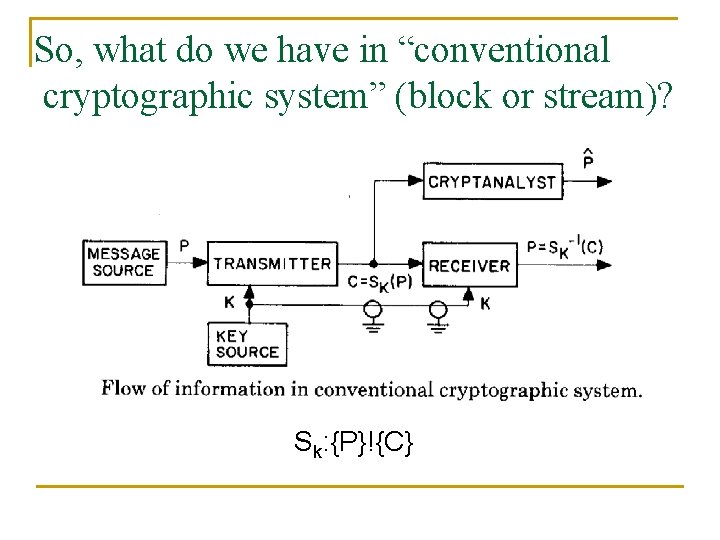
So, what do we have in “conventional cryptographic system” (block or stream)? Sk: {P}!{C}

“Conventional Cryptographic Goal: System” Enciphering and deciphering – “inexpensive”, but any “cryptananlytic operation” is “too complex to be economical”. “We call a task computationally infeasible, if its cost. . . is finite but impossibly large. ” Important desired property. Error propagation: “A small change in the input block produces a major change in the resulting output”.

“Conventional Cryptographic Threats: ({Sk} is known) System” Eavesdropping – “Ciphertext only”, “Known plaintext”, “Chosen plaintext”. Injecting – new messages, or combining/repeating. Problems: 1. Where does the secure channel comes from? 2. Authentication & Signature. 3. n users ) (n 2) keys.

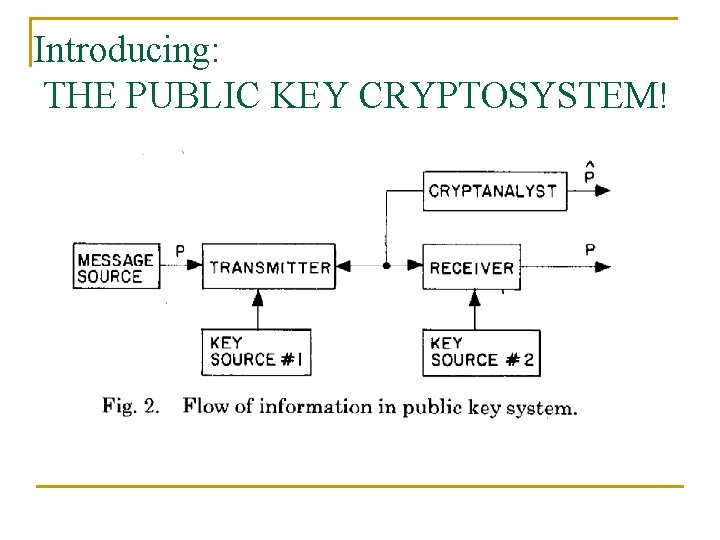
Introducing: THE PUBLIC KEY CRYPTOSYSTEM!

THE PUBLIC KEY CRYPTOSYSTEM! Two families {Ek}k, {Dk}k of invertible transformations, Ek, Dk: {M}!{M}, s. t. the following holds: 1. 8 k, Ek is the inverse of Dk. 2. 8 k, 8 m 2{M}, Ek(m), Dk(m), are “easy to compute”. 3. For almost every k, each easily computed algorithm equivalent Dk to is computationally infeasible to derive given Ek. 4. 8 k, it easy to come up with the pair h Dk, Ek i. RANDOMIZED! Publicize Ek, but keep Dk to yourself!

Suggestions 1. (useless) An invertible matrix E, D = E-1. (n 2 vs. n 3, at the time) 2. “One way compiler”. Public Key Distribution System: “Securely exchange a key over an insecure channel”. 3. Merkle. 4. The Diffie-Hellman key exchange.

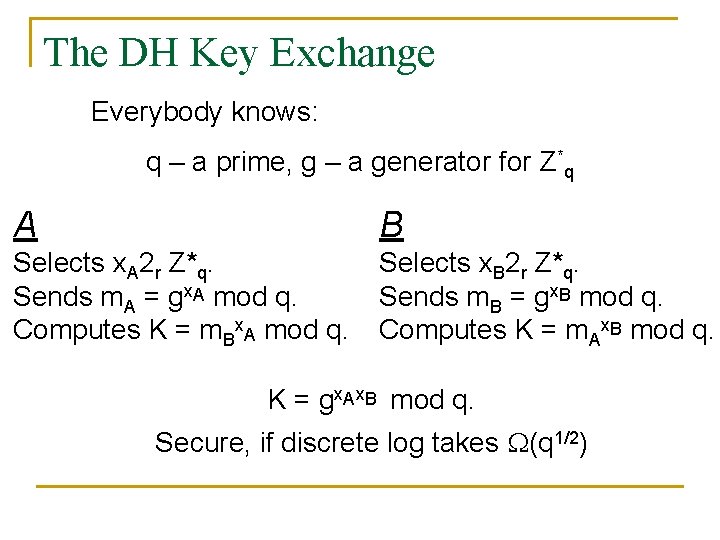
The DH Key Exchange Everybody knows: q – a prime, g – a generator for Z*q A B Selects x. A 2 r Z*q. Sends m. A = gx. A mod q. Computes K = m. Bx. A mod q. Selects x. B 2 r Z*q. Sends m. B = gx. B mod q. Computes K = m. Ax. B mod q. K = gx. Ax. B mod q. Secure, if discrete log takes (q 1/2)

Signature By public key cryptosystem! Just send - h m, Dk(m)i. One Way A function f is a one-way function if it is easy to compute f(x), but for almost every y it is “computationally infeasible to solve the equation y=f(x). ” (“Polynomials offer an elementary example of one-way functions. ” “One way functions are easy to devise. ”)

One Way Authentication Techniques: 1. Login: user picks PW, but sends f(PW). 2. Login revised: user picks PW, send f. T(PW). At time t, user authenticates by sending f. T-t(PW) (requires fast enumerations of f). 3. Select x 01, x 11, x 02, x 12, …, x 0 N, x 1 N. 4. Compute their images under f: y 01, y 11, y 02, y 12, …, y 0 N, y 1 N. Publicize these 2 N images. 5. Send the message m = m 1, m 2, …m. N and x 1 m 1, x 2 m 2, …, x. Nm. N

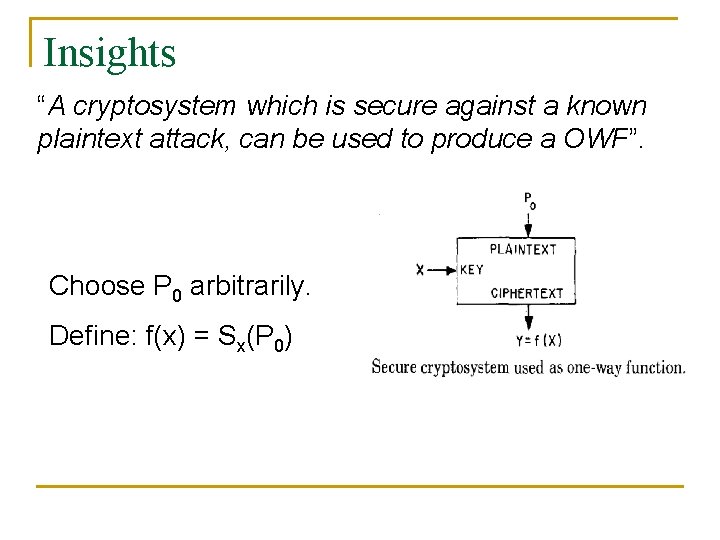
Insights “A cryptosystem which is secure against a known plaintext attack, can be used to produce a OWF”. Choose P 0 arbitrarily. Define: f(x) = Sx(P 0)

(. Insights (cont Trap-door OWF: a simply computed inverse exists, but given only f it is infeasible to find an inverse. Only possession of a trap-door information allows computing an inverse easily. (e. g. The random string used to produce E, D. ) (A quasi-OWF: same definition, without the trap-door information. ) Trap-door cipher: resists any cryptanalysis by anyone not in possession of a trap-door information. “A trap-door cryptosystem can be used to produce a public key distribution system”. A enciphers and publicize m, Ek(m), B breaks the encryption.

(. Insights (cont Public Key Cryptosystem ) OW authentication. “The converse does not appear to hold”. Public Key Cryptosystem ) Public Key Distribution System. “Not conversly”. Public Key Cryptosystem ) Trap-door OWF. The converse – the function “must be invertible”

Connection to Complexity “The cryptanalytic difficulty of a system whose encryption and decryption operations can be done in P time cannot be greater than NP”. Nondeterministically, choose the key (maybe also the message). Verify by encryption / decryption in polytime. “The general cryptanalytic problem is NP-complete. ” By Constructing a OWF from the Knapsack Problem.

The Knapsack Problem Given {a 1, a 2, …, an}, and x 2{0, 1}n, computing y=f(x)= iaixi is easy, yet finding a subset of {ai}i that sums up to a given y is NP-complete. Problems: 1. f cannot be degenerate. 2. f cannot be super-increasing. Is f hard on average? …Probably not. Knapsack based encryption – given `77 [Merkle, Hellman], broken `82 [Shamir] and later others.

Historical Note From Caesar cipher to WWII. References – a book [~ 1200 pages]: D. Kahn, The Codebreakers, The Story of Secret Writing. Emphasize the following point: “innovation has come primarily from the amateurs”. “We hope this will inspire others to work in this facinating area in which participation has been discouraged in the recent past by a nearly total government monopoly. ”

And what happened to Diffie & Hellman? Diffie didn't finish his degree, left to work in cryptography oriented companies. Works till today. Was awarded doctorate in 1992 (!) by the Swiss Federal IT. Hellman became a prof. in `79 and is currently retired. Both – highly respected, highly awarded.

After DH: Practical Public Keys Several suggestions, including the knapsack, and Mc. Eliece (ECC of invertible matrix and permutation + a random small mistake). 1978 – RSA! 1979 – Rabin (RSA with squaring) Mathematical definitions of security: 1982 -4 – Blum; Goldwasser & Micali.

Probabilistic Encryption Goldwasser & Micali ’ 84

Main contributions of this paper n First paper to give formal definitions of security n Chose an adversary with limited power (polynomial) n Showed equivalence of security definitions n Gave a construction which satisfies the definition and proved its security based on a common assumption (quadratic residuosity is hard)

Previous Attempts at Public Key Cryptography n DH ’ 76 n RSA ’ 78 n Rabin ‘ 79

Examples of Problems n Might be easy for some messages q q n Might reveal partial information q n In RSA, 1 and 0 always encrypt to themselves Small messages can be easily decrypted In RSA, the Jacobi symbol of the message is preserved under encryption Message Indistinguishability q q Given two messages m 1 and m 2 and their encryptions Ek(m 1) and Ek(m 2) – decide which is which No deterministic public key encryption gives message indistinguishability !!

Main Idea Make the Encryption Probabilistic ! n n Messages encrypt to many possible ciphertexts The encryption algorithm is probabilistic The decryption algorithm has a deterministic output Notice that any deterministic encryption can be converted into a randomized one q q part (length=l) of plaintext consist of a randomly generated bit-string not provably secure

Security Definitions n Polynomial security q q q no passive adversary can in polynomial time select two plaintext m 1 and m 2 and then distinguish between encryptions of m 1 and m 2 with probability greater than ½ +1/poly(k)

Security Definitions II n Semantically secure q q for all probability distributions over the message space whatever a passive adversary can compute in expected polynomial time about the plaintext given the ciphertext it can also compute in expected polynomial time without the ciphertext. Semantic security of PKC = no partial information leakage

Perfect vs. Semantic security n perfect secrecy: q q q n a passive adversary, even with infinite computational resources can learn nothing about plaintext from ciphertext Limitation: cannot be achieved unless key is as long as message semantic security: polynomially bounded perfect secrecy q q a passive adversary with poly. bounded resources can learn nothing semantically secure PKC where keys are shorter than messages

Unapproximable Trapdoor Predicates A family of unapproximable trapdoor predicates (UTP) is n a family of predicates {Bi(x)}i Which is unapproximable, i. e. , for any polynomially sized circuit C, Pr[C(x)=Bi(x)] <½+1/poly(k) And has a trapdoor q q q n n n given i and y=0, 1 can easily find x s. t. Bi(x)=y with uniform probability over the possible x There exists an algorithm T and a function (i) s. t. given ( (i), i, x) T can compute Bi(x) It is possible to select pairs (i, (i)) with uniform probability

A note on quadratic residuosity n n n y is a quadratic residue modulo n if y has a square root modulo n That is y=x 2 modulo n y is a quadratic non-residue modulo n if y doesn’t have a square root modulo n If n is prime, computing whether y is a quadratic residue is easy. The Legendre symbol (y/p) is defined to be 1 if y is a quadratic residue mod p and -1 otherwise The Jacobi symbol (y/n) is defined as (y/p 1)(y/p 2)…(y/pk)

A note on quadratic residuosity n n n Computing the Jacobi symbol is easy even if the factorization of n is not known !! Raising to an odd power preserves the Jacobi symbol y is a quadratic residue mod n iff (y/p 1)=(y/p 2)=1 But (y/n)=1 does not imply that y is a quadratic residue If (y/p 1)=(y/p 2)=-1 then (y/n)=1 but y is not a quadratic residue

Quadratic Residuosity as a UTP n n Private key ( (i)) is a pair of primes p 1, p 2 Public key (i) is n=p 1 p 2 and y – a quadratic nonresidue Qi(x) = 1 iff x is a quadratic residue modulo n Facts: q q q Qi(x) is hard to approximate Given p 1, p 2 it is easy to compute Qi(x) It is easy to generate residues with uniform probability Given a non-residue it is easy to generate nonresidues with uniform probability It is easy to generate p 1, p 2, y

PKC and PPKC n Public Key Cryptosystem (PKC) is composed of a server which given q q n MG – a message generator and a security parameter k Outputs, (E)ncryption and (D)ecryption algorithms Probabilistic PKC (PPKC) with UTP B q q q Outputs a pair (i, (i)) where i specifies the Encryption algorithm E, and (i) specifies the Decryption algorithm D E takes an l bit input m 1 m 2…ml for each mj, E randomly selects xj such that Bi(xj)=mj. The output is (x 1, x 2, …, xl) D takes (x 1, x 2, …, xl) and uses T to find mj for each xj (remember that T takes (x, i, (i)) and outputs Bi(x))

PPKC with Quadratic Residuosity n n Generates p 1, p 2 and y – a quadratic non-residue Outputs a pair (i, (i)) where i is (n=p 1 p 2 , y), and (i) = (p 1, p 2) The encryption algorithm generates for every bit mj of the message a xj s. t. , Qi(x)=mj and outputs (x 1, …, xl) The decryption algorithm takes (x 1, x 2, …, xl) and uses its knowledge of p 1, p 2 to find mj for each xj

Main Results n n Any PPKC with a UTP is polynomially secure A PKC is polynomially secure it is semantically secure

PPKC is Polynomially Secure n n Assume that an (polynomially bounded) adversary A can find two messages m 1, m 2 and them distinguish with non-negligible probability between Ei(m 1) and Ei(m 2) Look at a sequence of messages m 1=x 1, x 2, …, xt=m 2 s. t. xj and xj+1 differ by a single bit There must be j s. t. A can distinguish between Ei(xj) and Ei(xj+1) with non-negligible probability But now we can use this fact to contradict the unapproximability of Bi

PPKC is Polynomially Secure n n n Given y we can approximate Bi(y) by generating many messages which encrypt to Ei(xj) or Ei(xj+1) where the jth element of the message is y Since we can distinguish between encryptions of xj and xj+1 with non-negligible probability, we can approximate Bi(y) with non-negligible probability A contradiction to the unapproximability of Bi

Polynomially Secure Semantically Secure n n n Recall a PKC is semantically secure if for all message distributions and for all functions f and for all polynomially sized circuit C, given an encryption E(m) of m the probability that C(E(m)) = f(m) is at most the probability of f(m), up to a negligible factor (over the given message distribution). Let be a polynomially secure PKC and assume for a contradiction that is not semantically secure. So we have a polynomially sized circuit C that given E(m) can compute f(m) with probability higher than the probability of f(m) (over message distribution).

Polynomially Semantically n n n By the assumption we have advantage k=1/poly(k) Denote by r. Em, y the probability that C outputs y on input E(m) Fix some message Let M’ be the set of all messages m s. t. |r. Em, v-r. E , v| > 2/10 Lemma 1 q n Given m 2 M’ we can find v s. t. , |r. Em, v-r. E , v|> 2/20 in polynomial time Lemma 2 q m 2 M’ pm > k/10

Polynomially Semantically n Lemma 1 q n Lemma 2 q n n n Given m 2 M’ we can find v s. t. , |r. Em, v-r. E , v|> 2/20 in polynomial time m 2 M’ pm > k/10 Lemma 1 and 2 imply that we can find two messages m 1, m 2 and a value v s. t. , |r. Em 1, v-r. Em 2, v|> 2/20 But this allows us to distinguish between m 1 and m 2 in contradiction to the polynomially secure PKC Conclusion: polynomial security semantic security

Other solutions n n n Notice that every bit of the message is expanded into k bits in the encryption Using apseudo-random generator, it is possible to add a total of k bits to the entire message [GB 84’] Idea is to generate a random seed, and send the encryption of the seed together with the message xored with the pseudo-random output

Further development n Pseudo-random generators/functions [GGM 84’] n Interactive proofs/Zero knowledge [GMR 85’] n Digital Signatures [GMY ’ 83]

Thank You