Cryptography Lecture 11 Arpita Patra Generic Results in

Cryptography Lecture 11 Arpita Patra

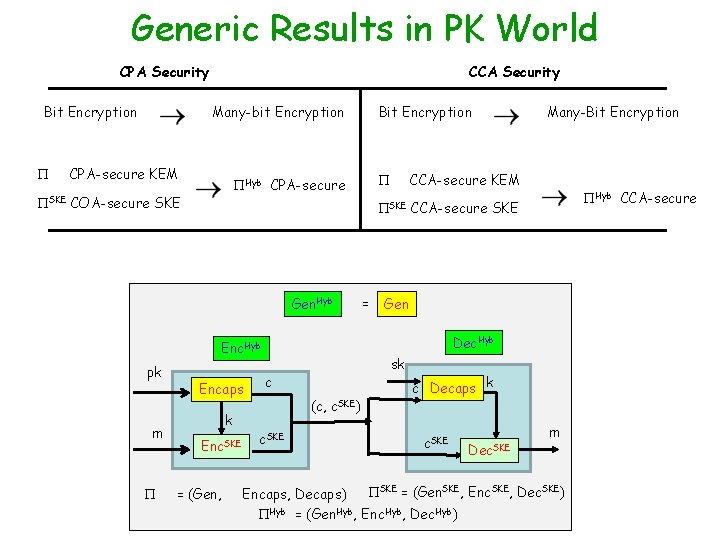
Generic Results in PK World CPA Security Bit Encryption CCA Security Many-bit Encryption CPA-secure KEM SKE Gen. Hyb m k Enc. SKE = (Gen, Hyb CCA-secure SKE Gen Dec. Hyb Encaps = Many-Bit Encryption CCA-secure KEM Hyb CPA-secure SKE COA-secure SKE pk Bit Encryption sk c (c, c. SKE) c. SKE c Decaps k c. SKE Dec. SKE m SKE = (Gen. SKE, Enc. SKE, Dec. SKE) Encaps, Decaps) Hyb = (Gen. Hyb, Enc. Hyb, Dec. Hyb)

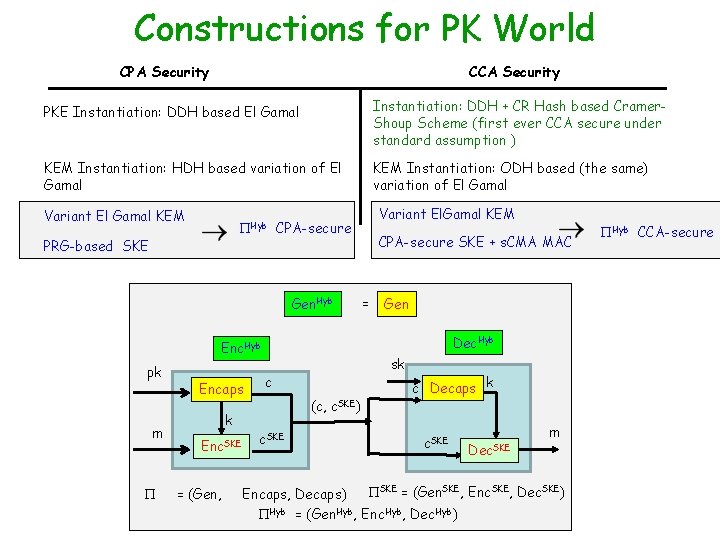
Constructions for PK World CPA Security CCA Security PKE Instantiation: DDH based El Gamal Instantiation: DDH + CR Hash based Cramer. Shoup Scheme (first ever CCA secure under standard assumption ) KEM Instantiation: HDH based variation of El Gamal KEM Instantiation: ODH based (the same) variation of El Gamal Variant El Gamal KEM Hyb PRG-based SKE CPA-secure Gen. Hyb m Encaps k Enc. SKE = (Gen, CPA-secure SKE + s. CMA MAC = Gen Dec. Hyb Enc. Hyb pk Variant El. Gamal KEM sk c (c, c. SKE) c. SKE c Decaps k c. SKE Dec. SKE m SKE = (Gen. SKE, Enc. SKE, Dec. SKE) Encaps, Decaps) Hyb = (Gen. Hyb, Enc. Hyb, Dec. Hyb) Hyb CCA-secure

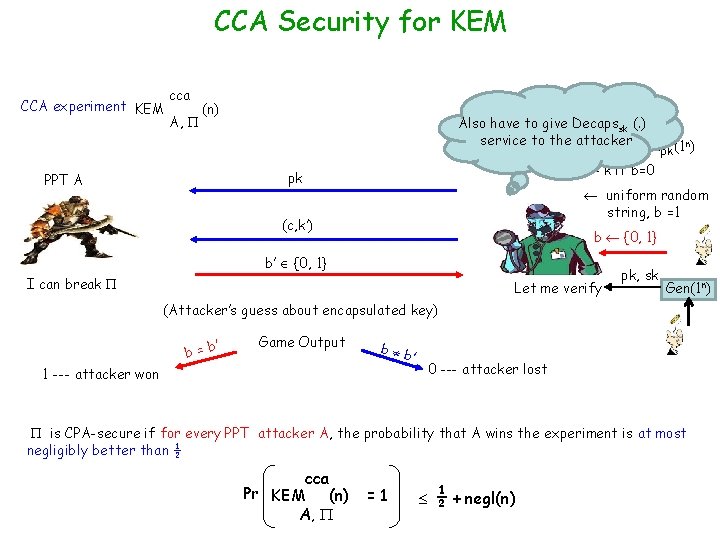
CCA Security for KEM CCA experiment KEM cca A, (n) = (Gen, Encaps, Decaps) Also have to give Decapssk (. ) service to the(c, k) attacker Encapspk(1 n) k’ k if b=0 pk PPT A uniform random string, b =1 (c, k’) b {0, 1} b’ {0, 1} I can break Let me verify pk, sk Gen(1 n) (Attacker’s guess about encapsulated key) ’ b=b Game Output b b ’ 1 --- attacker won 0 --- attacker lost is CPA-secure if for every PPT attacker A, the probability that A wins the experiment is at most negligibly better than ½ cca Pr KEM (n) A, =1 ½ + negl(n)

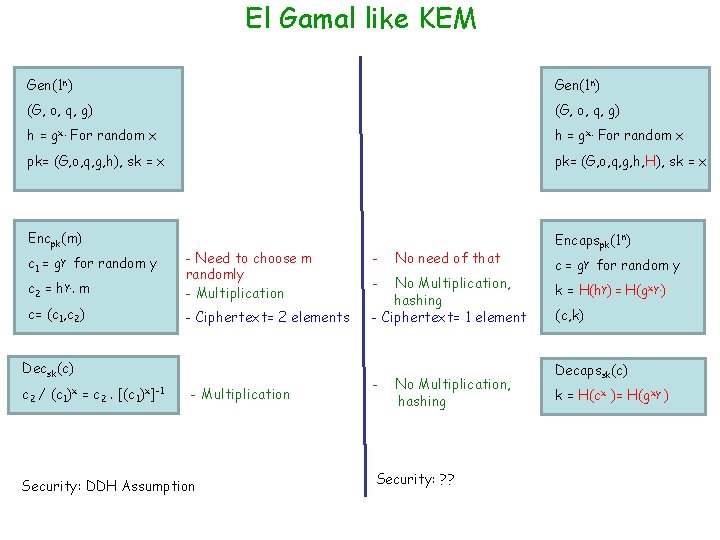
El Gamal like KEM Gen(1 n) (G, o, q, g) h = gx. For random x pk= (G, o, q, g, h), sk = x pk= (G, o, q, g, h, H), sk = x Encpk(m) Encapspk(1 n) c 2 = hy. . m - Need to choose m randomly - Multiplication c= (c 1, c 2) - Ciphertext= 2 elements c 1 = gy for random y Decsk(c) c 2 / (c 1)x = c 2. [(c 1)x]-1 - Multiplication Security: DDH Assumption - No need of that - No Multiplication, hashing - Ciphertext= 1 element - No Multiplication, hashing Security: ? ? c = gy for random y k = H(hy) = H(gxy. ) (c, k) Decapssk(c) k = H(cx )= H(gxy )

El Gamal like KEM Gen(1 n) (G, o, q, g) h = gx. For random x pk= (G, o, q, g, h, H), sk = x Encapspk(1 n) c = gy for random y k= H(hy) = H(gxy. ) Decsk(c) k = H(cx )= H(gxy ) (c, k) ODH (Oracle Diffie-Hellman) Assumption ODH problem is hard relative to (G, o) and hash function H: G -> {0, 1} m if for every PPT A, (it is hard to distinguish H(gxy) from a random string {0, 1}m even given gx, gy AND an oracle Oy(X): = H(Xy); anything other than gx can be quired) ): | Pr[Ao y(. ) (G, o, q, g, gx, gy, H(gxy )) = 1] - Pr[Aoy(. ) (G, o, q, g, gx, gy, r ) = 1] | negl() ODH assumption is just the belief that there exist a group and hash function H so that the above is true. It is stronger than HDH. Theorem: ODH assumption holds is a CCA-secure KEM

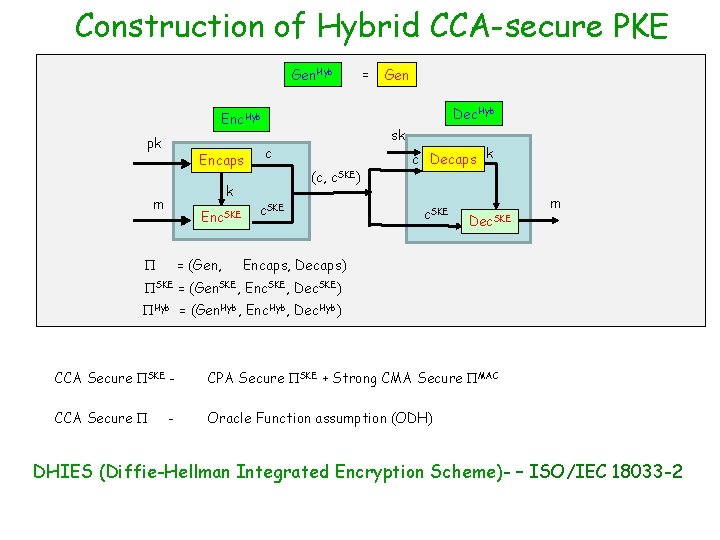
Construction of Hybrid CCA-secure PKE Gen. Hyb Encaps k m Enc. SKE = (Gen, Gen Dec. Hyb Enc. Hyb pk = sk c (c, c. SKE) c. SKE c Decaps k c. SKE Dec. SKE m Encaps, Decaps) SKE = (Gen. SKE, Enc. SKE, Dec. SKE) Hyb = (Gen. Hyb, Enc. Hyb, Dec. Hyb) CCA Secure SKE - CPA Secure SKE + Strong CMA Secure MAC CCA Secure Oracle Function assumption (ODH) - DHIES (Diffie-Hellman Integrated Encryption Scheme)- – ISO/IEC 18033 -2

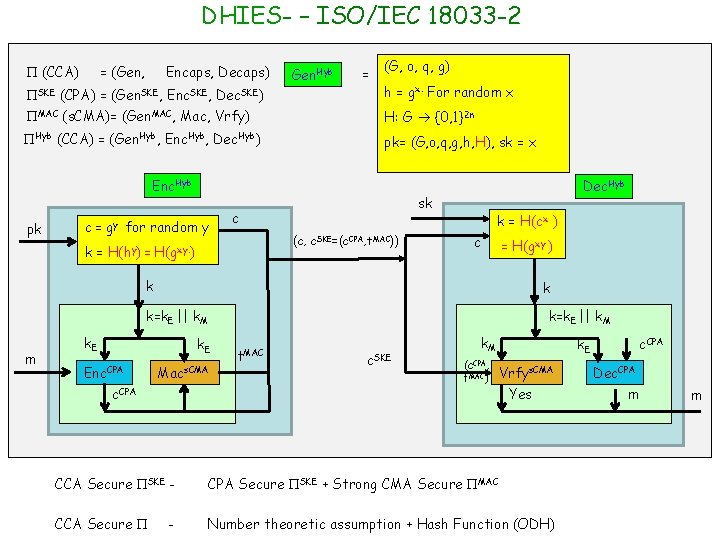
DHIES- – ISO/IEC 18033 -2 (CCA) = (Gen, Encaps, Decaps) Gen. Hyb = (G, o, q, g) SKE (CPA) = (Gen. SKE, Enc. SKE, Dec. SKE) h = gx. For random x MAC (s. CMA)= (Gen. MAC, Mac, Vrfy) H: G {0, 1}2 n Hyb (CCA) = (Gen. Hyb, Enc. Hyb, Dec. Hyb) pk= (G, o, q, g, h, H), sk = x Enc. Hyb pk c = gy for random y k= sk c (c, c. SKE=(c. CPA, t. MAC)) H(hy) = H(gxy. ) Dec. Hyb k = H(cx ) c = H(gxy ) k k k=k. E || k. M m k. E Enc. CPA Macs. CMA c. CPA k=k. E || k. M t. MAC c. SKE k. M (c. CPA, t. MAC) k. E Vrfys. CMA Yes CCA Secure SKE - CPA Secure SKE + Strong CMA Secure MAC CCA Secure Number theoretic assumption + Hash Function (ODH) - c. CPA Dec. CPA m m

DHIES (Term Paper) Michel Abdalla, Mihir Bellare, Phillip Rogaway: The Oracle Diffie-Hellman Assumptions and an Analysis of DHIES. CT-RSA 2001: 143 -158

Cramer-Shoup Cryptosystem Ronald Cramer, Victor Shoup: A Practical Public Key Cryptosystem Provably Secure Against Adaptive Chosen Ciphertext Attack. CRYPTO 1998: 13 -25

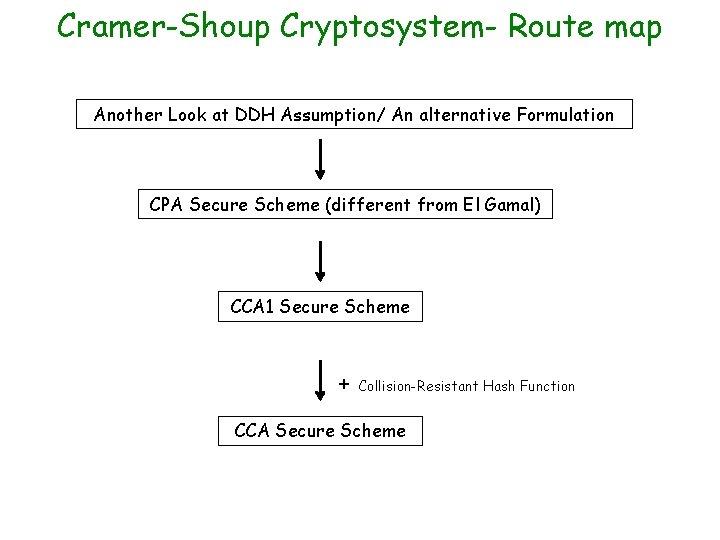
Cramer-Shoup Cryptosystem- Route map Another Look at DDH Assumption/ An alternative Formulation CPA Secure Scheme (different from El Gamal) CCA 1 Secure Scheme + Collision-Resistant Hash Function CCA Secure Scheme

Another Look at DDH (G, o, q, g) – Group of Prime Order q | Pr[A(g, gx, gy, gxy ) = 1] - (g 0, g 1, g 0 y, g 1 y ) | Pr[A(g , g 1, g r ) = 1] 0 0 1 Pr[A(g, gx, gy, gz ) = 1] | negl() (g 0, g 1, g 0 y, g 1 y’ ) - Pr[A(g 0, g 1, g 0 r, g 1 r’ ) = 1] | negl()

Randomization Function Input Output (g 0, g 1, h 0, h 1 ) Random (x, y) from Zq u = g 0 x. g 1 y Way 1: Given x, y, h 0 , h 1 v = h 0 x. h 1 y Way 2: Given r, u Case I (g 0, g 1, h 0 = g 0 r , h 1 = g 1 r): Claim: ur = v Proof: ur = (g 0 x. g 1 y)r = h 0 x. h 1 y = v Case II (g 0, g 1, h 0 = g 0 r , h 1 = g 1 r’ ): Claim: An all powerful adv A can guess v with probability at most 1/|G|, even given (g 0, g 1, h 0, h 1, u). Proof: A can compute r, r’, α (where g 1 = g 0α) and discrete log of u (say R) u = g 0 R = (g 0 x. g 1 y) = g 0 x +αy = R --- (1) v = h 0 x. h 1 y = g 0 rx. g 1 r’y = g 0 rx +αr’y is linearly independent of x +αy For every guess R’ of this value rx +αr’y, there exist a pair of unique values for x, y satisfying equation (1)

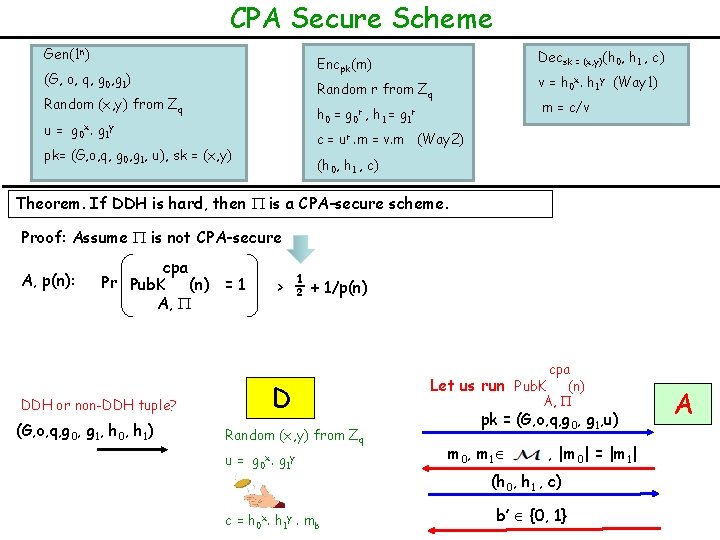
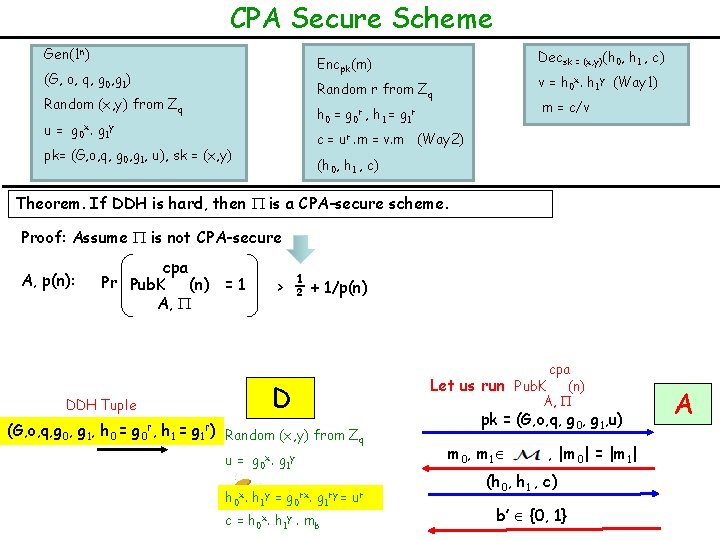
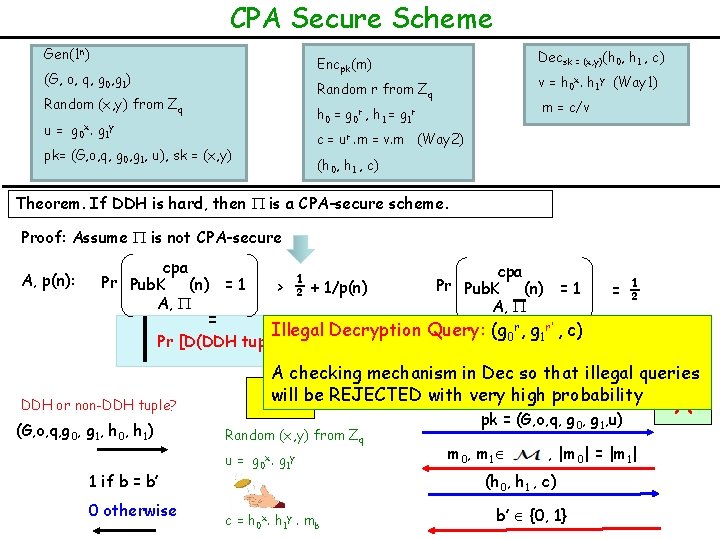
CPA Secure Scheme Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, DDH or non-DDH tuple? (G, o, q, g 0, g 1, h 0, h 1) > ½ + 1/p(n) D Random (x, y) from Zq u = g 0 x. g 1 y c = h 0 x. h 1 y. mb cpa Let us run Pub. K (n) A, pk = (G, o, q, g 0, g 1, u) m 0, m 1 , |m 0| = |m 1| (h 0, h 1 , c) b’ {0, 1} A

CPA Secure Scheme Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, ½ + 1/p(n) > cpa Let us run Pub. K (n) A, D DDH Tuple (G, o, q, g 0, g 1, h 0 = g 0 r, h 1 = g 1 r) Random (x, y) from Zq u = g 0 x. g 1 y h 0 x. h 1 y = g 0 rx. g 1 ry = c = h 0 x. h 1 y. mb ur pk = (G, o, q, g 0, g 1, u) m 0, m 1 , |m 0| = |m 1| (h 0, h 1 , c) b’ {0, 1} A

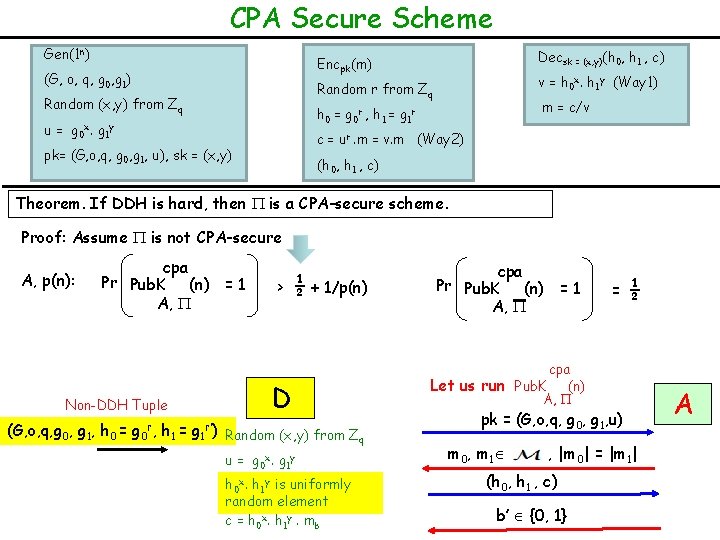
CPA Secure Scheme Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, Non-DDH Tuple > ½ + 1/p(n) D (G, o, q, g 0, g 1, h 0 = g 0 r, h 1 = g 1 r’) Random (x, y) from Zq u = g 0 x. g 1 y h 0 x. h 1 y is uniformly random element c = h 0 x. h 1 y. mb cpa Pr Pub. K (n) = 1 A, = ½ cpa Let us run Pub. K (n) A, pk = (G, o, q, g 0, g 1, u) m 0, m 1 , |m 0| = |m 1| (h 0, h 1 , c) b’ {0, 1} A

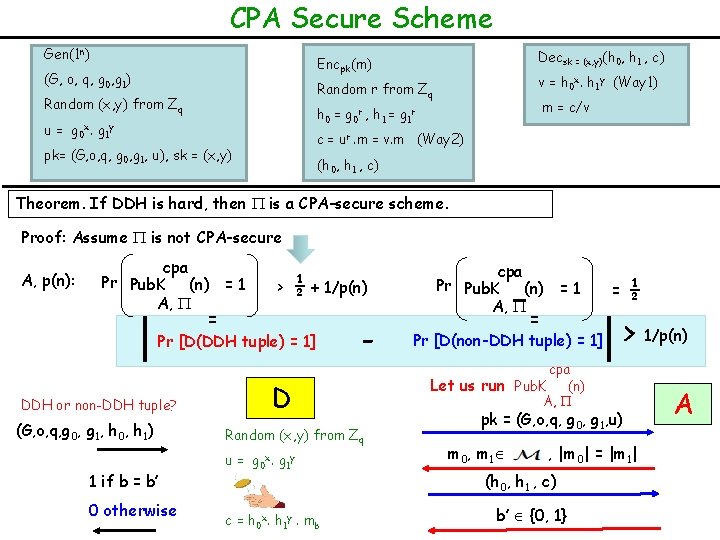
CPA Secure Scheme Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, > ½ + 1/p(n) = Pr [D(DDH tuple) = 1] DDH or non-DDH tuple? (G, o, q, g 0, g 1, h 0, h 1) 1 if b = b’ 0 otherwise - D Random (x, y) from Zq u = g 0 x. g 1 y c = h 0 x. h 1 y. mb cpa Pr Pub. K (n) = 1 A, = Pr [D(non-DDH tuple) = 1] ½ = > 1/p(n) cpa Let us run Pub. K (n) A, pk = (G, o, q, g 0, g 1, u) m 0, m 1 , |m 0| = |m 1| (h 0, h 1 , c) b’ {0, 1} A

Why NOT El Gamal? Gen(1 n) Encpk(m) (G, o, q, g) Random x from Zq, c 1 = h = gx gy Decsk(c) for random y c 2 / (c 1)x = c 2. [(c 1)x]-1 c 2 = gxy. . m pk= (G, o, q, g 0, h), sk = x Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, > = cpa Pr Pub. K (n) = 1 A, ½ + 1/p(n) Pr [D(DDH tuple) = 1] - = Pr [D(non-DDH tuple) = 1] The secret key is not with the reduction and so cannot Let us run DDH or non-DDH tuple? provide DO service to A! (G, o, q, g, g x, g y, gz) D 0 otherwise , |m 0| = |m 1| c = (gy, gz. mb) 1 if b = b’ b ½ > 1/p(n) cpa Pub. K (n) A, pk = (G, o, q, g, gx) m 0, m 1 = b’ {0, 1} A

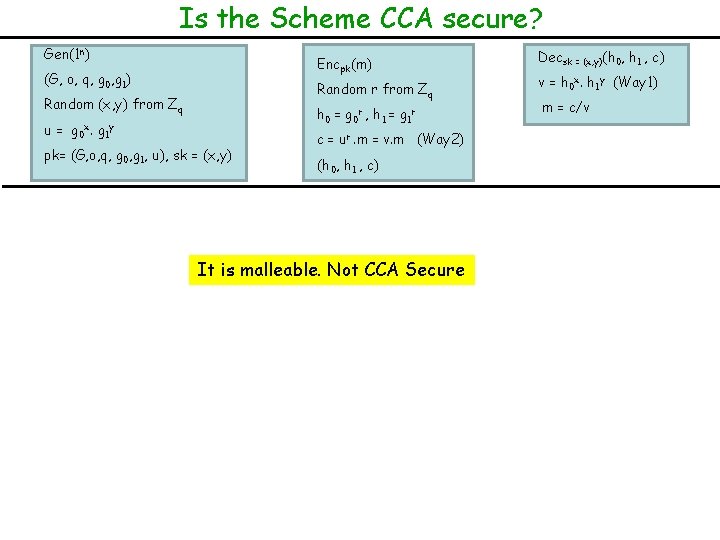
Is the Scheme CCA secure? Gen(1 n) Encpk(m) (G, o, q, g 0, g 1) Random r from Zq Random (x, y) from Zq h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y pk= (G, o, q, g 0, g 1, u), sk = (x, y) c = ur. m = v. m (Way 2) (h 0, h 1 , c) It is malleable. Not CCA Secure Decsk = (x, y)(h 0, h 1 , c) v = h 0 x. h 1 y (Way 1) m = c/v

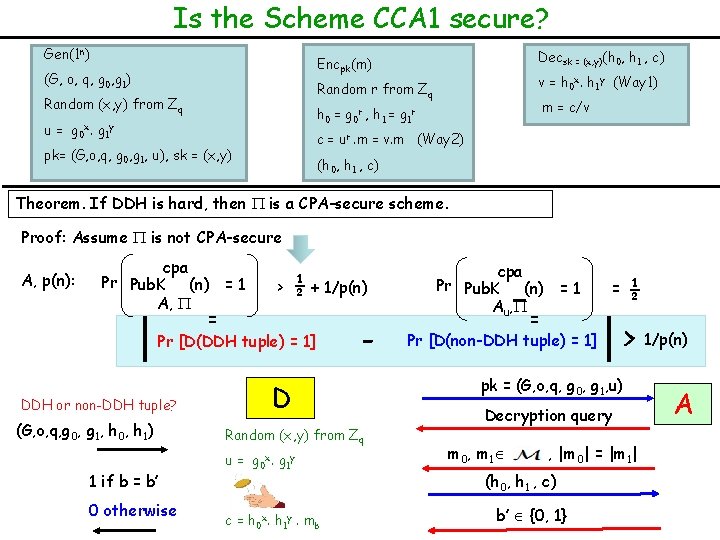
Is the Scheme CCA 1 secure? Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, > ½ + 1/p(n) = Pr [D(DDH tuple) = 1] DDH or non-DDH tuple? (G, o, q, g 0, g 1, h 0, h 1) 1 if b = b’ 0 otherwise - D Random (x, y) from Zq u = g 0 x. g 1 y c = h 0 x. h 1 y. mb cpa Pr Pub. K (n) = 1 Au, ½ = = Pr [D(non-DDH tuple) = 1] > 1/p(n) pk = (G, o, q, g 0, g 1, u) Decryption query m 0, m 1 , |m 0| = |m 1| (h 0, h 1 , c) b’ {0, 1} A

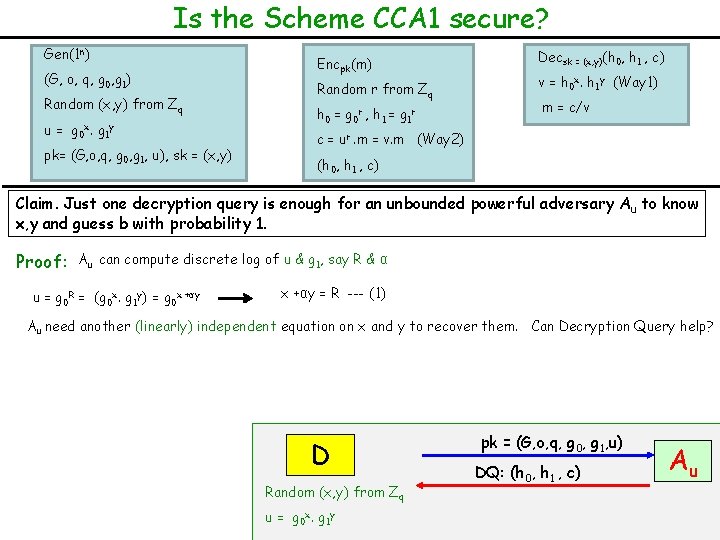
Is the Scheme CCA 1 secure? Gen(1 n) (G, o, q, g 0, g 1) Random (x, y) from Zq u = g 0 x. g 1 y pk= (G, o, q, g 0, g 1, u), sk = (x, y) Encpk(m) Random r from Zq h 0 = g 0 r , h 1 = g 1 r Decsk = (x, y)(h 0, h 1 , c) v = h 0 x. h 1 y (Way 1) m = c/v c = ur. m = v. m (Way 2) (h 0, h 1 , c) Claim. Just one decryption query is enough for an unbounded powerful adversary A u to know x, y and guess b with probability 1. Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x. g 1 y) = g 0 x +αy = R --- (1) Au need another (linearly) independent equation on x and y to recover them. Can Decryption Query help? D Random (x, y) from Zq u = g 0 x. g 1 y pk = (G, o, q, g 0, g 1, u) DQ: (h 0, h 1 , c) Au

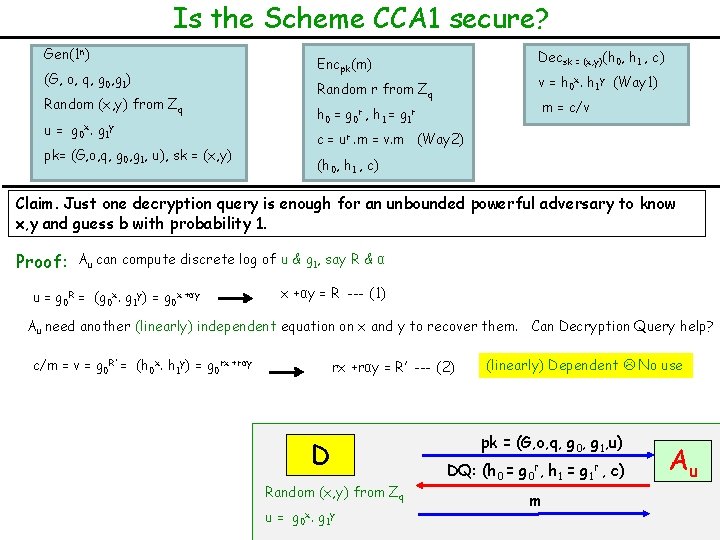
Is the Scheme CCA 1 secure? Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Claim. Just one decryption query is enough for an unbounded powerful adversary to know x, y and guess b with probability 1. Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x. g 1 y) = g 0 x +αy = R --- (1) Au need another (linearly) independent equation on x and y to recover them. Can Decryption Query help? c/m = v = g 0 R’ = (h 0 x. h 1 y) = g 0 rx +rαy = R’ --- (2) D Random (x, y) from Zq u= g 0 x. g 1 y (linearly) Dependent No use pk = (G, o, q, g 0, g 1, u) DQ: (h 0 = g 0 r, h 1 = g 1 r , c) m Au

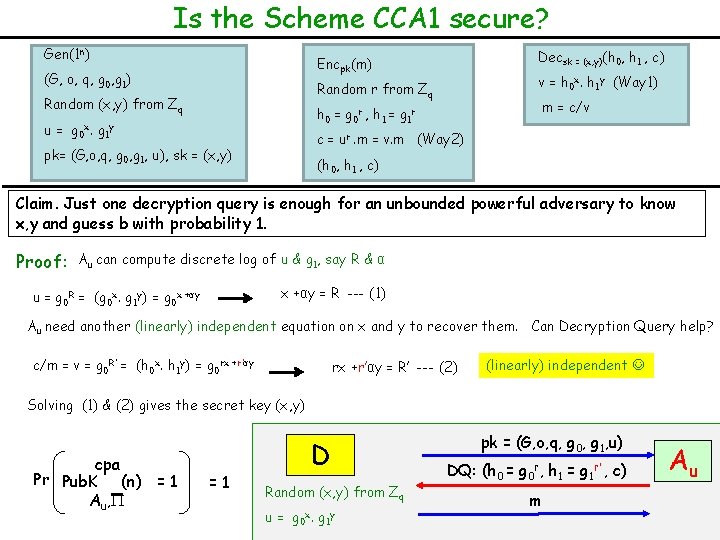
Is the Scheme CCA 1 secure? Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Claim. Just one decryption query is enough for an unbounded powerful adversary to know x, y and guess b with probability 1. Proof: Au can compute discrete log of u & g 1, say R & α x +αy = R --- (1) u = g 0 R = (g 0 x. g 1 y) = g 0 x +αy Au need another (linearly) independent equation on x and y to recover them. Can Decryption Query help? c/m = v = g 0 R’ = (h 0 x. h 1 y) = g 0 rx +r’αy = R’ --- (2) (linearly) independent Solving (1) & (2) gives the secret key (x, y) cpa Pr Pub. K (n) = 1 Au, =1 D Random (x, y) from Zq u= g 0 x. g 1 y pk = (G, o, q, g 0, g 1, u) DQ: (h 0 = g 0 r, h 1 = g 1 r’ , c) m Au

CPA Secure Scheme Gen(1 n) Decsk = (x, y)(h 0, h 1 , c) Encpk(m) (G, o, q, g 0, g 1) v = h 0 x. h 1 y (Way 1) Random r from Zq Random (x, y) from Zq m = c/v h 0 = g 0 r , h 1 = g 1 r u = g 0 x. g 1 y c = ur. m = v. m (Way 2) pk= (G, o, q, g 0, g 1, u), sk = (x, y) (h 0, h 1 , c) Theorem. If DDH is hard, then is a CPA-secure scheme. Proof: Assume is not CPA-secure A, p(n): cpa Pr Pub. K (n) = 1 A, = > ½ + 1/p(n) = Illegal Decryption Query: (g 0 r, g 1 r’ , c) Pr [D(DDH tuple) = 1] DDH or non-DDH tuple? (G, o, q, g 0, g 1, h 0, h 1) 1 if b = b’ 0 otherwise cpa Pr Pub. K (n) = 1 A, - Pr [D(non-DDH tuple) = 1] ½ = > 1/p(n) cpa illegal queries A checking mechanism in Dec so that Let us run Pub. K (n) will be REJECTED with very high. A, probability D Random (x, y) from Zq u = g 0 x. g 1 y c = h 0 x. h 1 y. mb pk = (G, o, q, g 0, g 1, u) m 0, m 1 , |m 0| = |m 1| (h 0, h 1 , c) b’ {0, 1} A

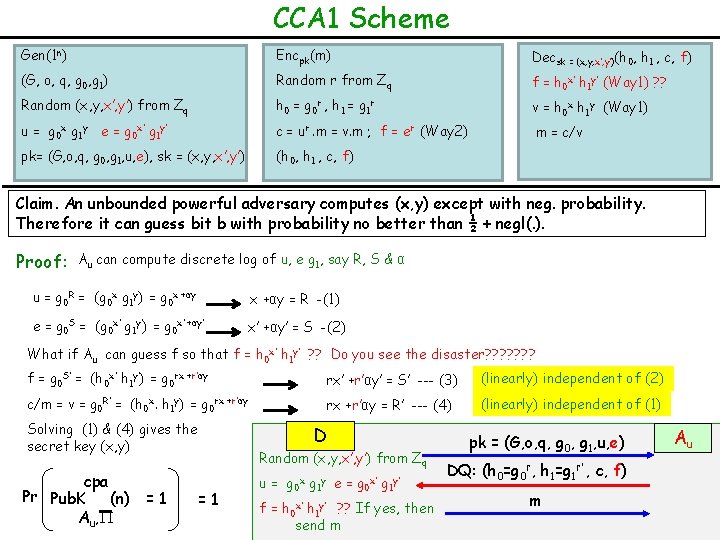
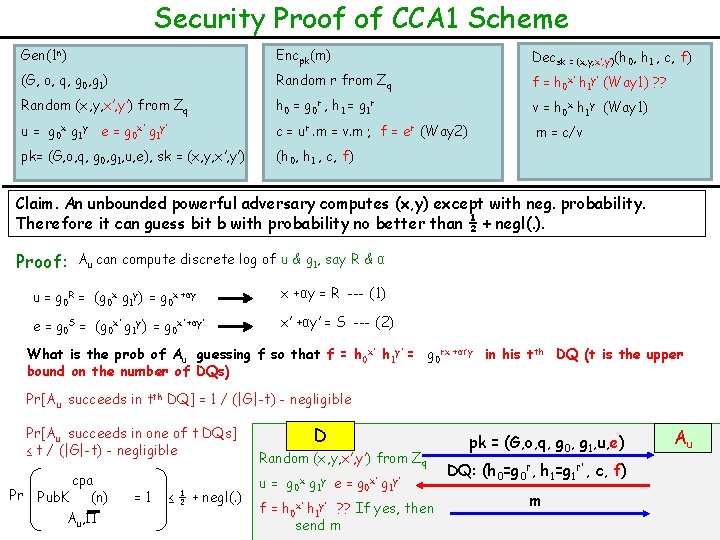
CCA 1 Scheme Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’)(h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ c = ur. m = v. m ; f = er (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e), sk = (x, y, x’, y’) (h 0, h 1 , c, f) Claim. An unbounded powerful adversary computes (x, y) except with neg. probability. Therefore it can guess bit b with probability no better than ½ + negl(. ). Proof: Au can compute discrete log of u, e g 1, say R, S & α u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R -(1) e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S -(2) What if Au can guess f so that f = h 0 x’ h 1 y’ ? ? Do you see the disaster? ? ? ? f = g 0 S’ = (h 0 x’ h 1 y’) = g 0 rx +r’αy rx’ +r’αy’ = S’ --- (3) (linearly) independent of (2) c/m = v = g 0 R’ = (h 0 x. h 1 y) = g 0 rx +r’αy = R’ --- (4) (linearly) independent of (1) Solving (1) & (4) gives the secret key (x, y) cpa Pr Pub. K (n) = 1 Au, =1 D Random (x, y, x’, y’) from Zq u= g 0 x g 1 y e= g 0 x’ g 1 y’ f = h 0 x’ h 1 y’ ? ? If yes, then send m pk = (G, o, q, g 0, g 1, u, e) DQ: (h 0=g 0 r, h 1=g 1 r’ , c, f) m Au

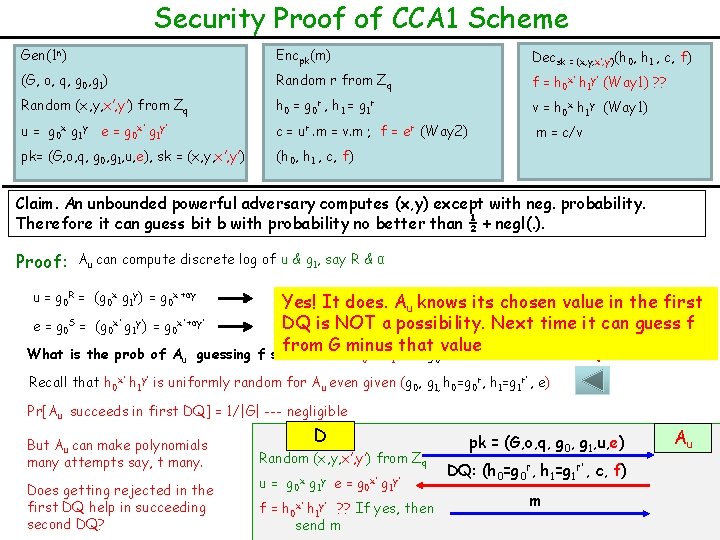
Security Proof of CCA 1 Scheme Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’)(h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ c = ur. m = v. m ; f = er (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e), sk = (x, y, x’, y’) (h 0, h 1 , c, f) Claim. An unbounded powerful adversary computes (x, y) except with neg. probability. Therefore it can guess bit b with probability no better than ½ + negl(. ). Proof: Au can compute discrete log of u & g 1, say R & α x +αy = R --- (1) u = g 0 R = (g 0 x g 1 y) = g 0 x +αy e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ What is the prob of Au guessing f Yes! It does. Au knows its chosen value in the first x’ +αy’is= NOT S --- (2) DQ a possibility. Next time it can guess f from G minus that value so that f = h x’ h y’ = g rx +αr’y in his FIRST DQ 0 1 0 Recall that h 0 x’ h 1 y’ is uniformly random for Au even given (g 0, g 1, h 0=g 0 r, h 1=g 1 r’ , e) Pr[Au succeeds in first DQ] = 1/|G| --- negligible But Au can make polynomials many attempts say, t many. Does getting rejected in the first DQ help in succeeding second DQ? D Random (x, y, x’, y’) from Zq u= g 0 x g 1 y e= g 0 x’ g 1 y’ f = h 0 x’ h 1 y’ ? ? If yes, then send m pk = (G, o, q, g 0, g 1, u, e) DQ: (h 0=g 0 r, h 1=g 1 r’ , c, f) m Au

Security Proof of CCA 1 Scheme Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’)(h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ c = ur. m = v. m ; f = er (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e), sk = (x, y, x’, y’) (h 0, h 1 , c, f) Claim. An unbounded powerful adversary computes (x, y) except with neg. probability. Therefore it can guess bit b with probability no better than ½ + negl(. ). Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R --- (1) e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S --- (2) What is the prob of Au guessing f so that f = h 0 x’ h 1 y’ = g 0 rx +αr’y in his SECOND DQ Pr[Au succeeds in second DQ] = 1 / (|G|-1) - negligible D Random (x, y, x’, y’) from Zq u= g 0 x g 1 y e= g 0 x’ g 1 y’ f = h 0 x’ h 1 y’ ? ? If yes, then send m pk = (G, o, q, g 0, g 1, u, e) DQ: (h 0=g 0 r, h 1=g 1 r’ , c, f) m Au

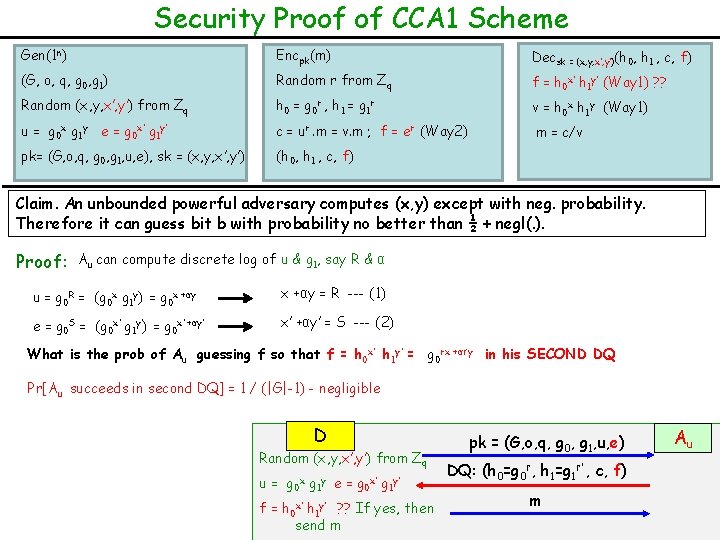
Security Proof of CCA 1 Scheme Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’)(h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ c = ur. m = v. m ; f = er (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e), sk = (x, y, x’, y’) (h 0, h 1 , c, f) Claim. An unbounded powerful adversary computes (x, y) except with neg. probability. Therefore it can guess bit b with probability no better than ½ + negl(. ). Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R --- (1) e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S --- (2) What is the prob of Au guessing f so that f = h 0 x’ h 1 y’ = g 0 rx +αr’y in his tth DQ (t is the upper bound on the number of DQs) Pr[Au succeeds in tth DQ] = 1 / (|G|-t) - negligible Pr[Au succeeds in one of t DQs] ≤ t / (|G|-t) - negligible Pr cpa Pub. K (n) Au, =1 ≤ ½ + negl(. ) D Random (x, y, x’, y’) from Zq u= g 0 x g 1 y e= g 0 x’ g 1 y’ f = h 0 x’ h 1 y’ ? ? If yes, then send m pk = (G, o, q, g 0, g 1, u, e) DQ: (h 0=g 0 r, h 1=g 1 r’ , c, f) m Au

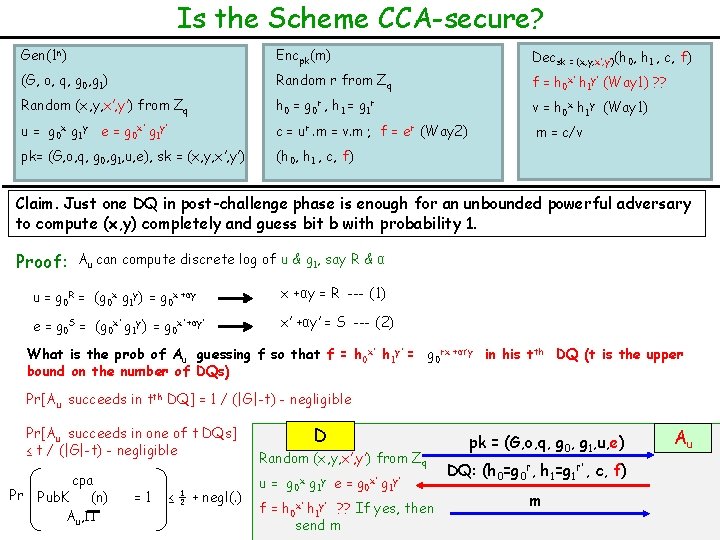
Is the Scheme CCA-secure? Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’)(h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ c = ur. m = v. m ; f = er (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e), sk = (x, y, x’, y’) (h 0, h 1 , c, f) Claim. Just one DQ in post-challenge phase is enough for an unbounded powerful adversary to compute (x, y) completely and guess bit b with probability 1. Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R --- (1) e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S --- (2) What is the prob of Au guessing f so that f = h 0 x’ h 1 y’ = g 0 rx +αr’y in his tth DQ (t is the upper bound on the number of DQs) Pr[Au succeeds in tth DQ] = 1 / (|G|-t) - negligible Pr[Au succeeds in one of t DQs] ≤ t / (|G|-t) - negligible Pr cpa Pub. K (n) Au, =1 ≤ ½ + negl(. ) D Random (x, y, x’, y’) from Zq u= g 0 x g 1 y e= g 0 x’ g 1 y’ f = h 0 x’ h 1 y’ ? ? If yes, then send m pk = (G, o, q, g 0, g 1, u, e) DQ: (h 0=g 0 r, h 1=g 1 r’ , c, f) m Au

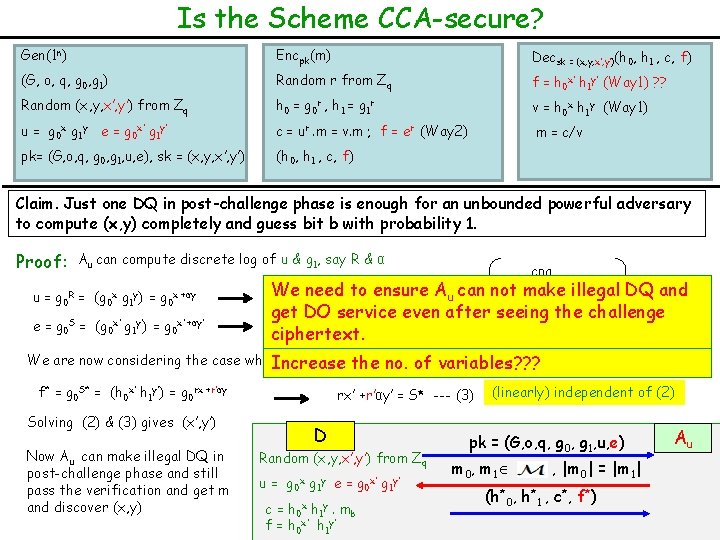
Is the Scheme CCA-secure? Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’)(h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ c = ur. m = v. m ; f = er (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e), sk = (x, y, x’, y’) (h 0, h 1 , c, f) Claim. Just one DQ in post-challenge phase is enough for an unbounded powerful adversary to compute (x, y) completely and guess bit b with probability 1. Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x g 1 y) = g 0 x +αy e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ cpa Pr not = 1 and Pub. Kmake (n) illegal = 1 DQ We need to (1) ensure Au can x +αy = R --Au, the challenge get DO service even after seeing x’ +αy’ = S --- (2) ciphertext. We are now considering the case when. Increase D receivedthe a non-DDH (g 0, g 1, h*0, h*1) and so h*0=g 0 r, h*1=g 1 r’ no. oftuple variables? ? ? f* = g 0 S* = (h 0 x’ h 1 y’) = g 0 rx +r’αy rx’ +r’αy’ = S* --- (3) Solving (2) & (3) gives (x’, y’) Now Au can make illegal DQ in post-challenge phase and still pass the verification and get m and discover (x, y) D Random (x, y, x’, y’) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ c= f= h 0 x h 1 y. h 0 x’ h 1 y’ mb (linearly) independent of (2) pk = (G, o, q, g 0, g 1, u, e) m 0, m 1 , |m 0| = |m 1| (h*0, h*1 , c*, f*) Au

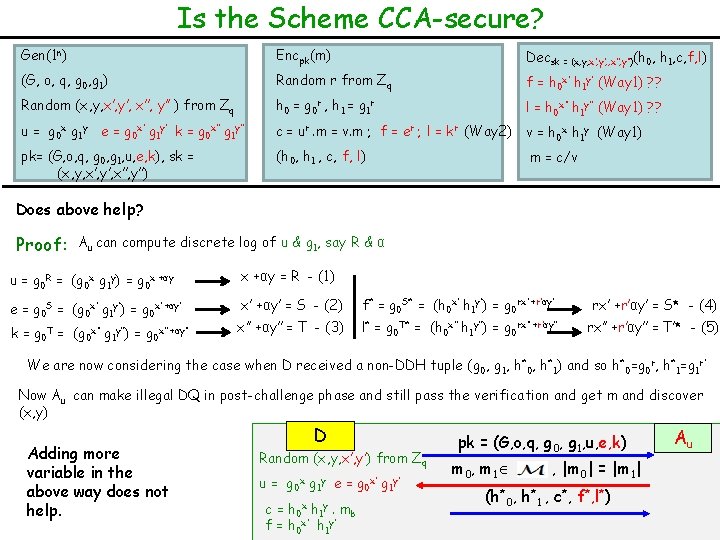
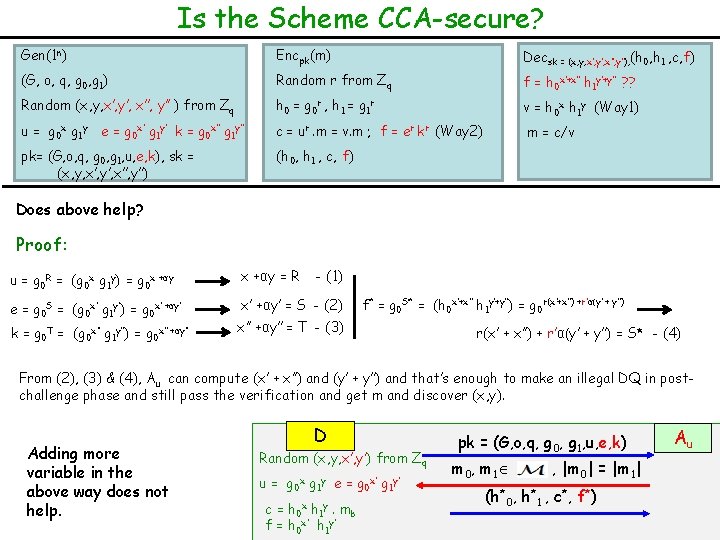
Is the Scheme CCA-secure? Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’, , x’’, y’’)(h 0, h 1, c, f, l) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’ h 1 y’ (Way 1) ? ? Random (x, y, x’, y’, x’’, y’’ ) from Zq h 0 = g 0 r , h 1 = g 1 r l = h 0 x’’ h 1 y’’ (Way 1) ? ? u = g 0 x g 1 y e = g 0 x’ g 1 y’ k = g 0 x’’ g 1 y’’ c = ur. m = v. m ; f = er ; l = kr (Way 2) v = h 0 x h 1 y (Way 1) pk= (G, o, q, g 0, g 1, u, e, k), sk = (x, y, x’, y’, x’’, y’’) (h 0, h 1 , c, f, l) m = c/v Does above help? Proof: Au can compute discrete log of u & g 1, say R & α u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R - (1) e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S - (2) f* = g 0 S* = (h 0 x’ h 1 y’) = g 0 rx’ +r’αy’ = S* - (4) x’’ +αy’’ = T - (3) l* = g 0 T* = (h 0 x’’ h 1 y’’) = g 0 rx’’ +r’αy’’ = T’* - (5) k = g 0 T = (g 0 x’’ g 1 y’’) = g 0 x’’ +αy’’ We are now considering the case when D received a non-DDH tuple (g 0, g 1, h*0, h*1) and so h*0=g 0 r, h*1=g 1 r’ Now Au can make illegal DQ in post-challenge phase and still pass the verification and get m and discover (x, y) Adding more variable in the above way does not help. D Random (x, y, x’, y’) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ c= f= h 0 x h 1 y. h 0 x’ h 1 y’ mb pk = (G, o, q, g 0, g 1, u, e, k) m 0, m 1 , |m 0| = |m 1| (h*0, h*1 , c*, f*, l*) Au

Is the Scheme CCA-secure? Gen(1 n) Encpk(m) Decsk = (x, y, x’, y’, x’’, y’’), (h 0, h 1 , c, f) (G, o, q, g 0, g 1) Random r from Zq f = h 0 x’+x’’ h 1 y’+y’’ ? ? Random (x, y, x’, y’, x’’, y’’ ) from Zq h 0 = g 0 r , h 1 = g 1 r v = h 0 x h 1 y (Way 1) u = g 0 x g 1 y e = g 0 x’ g 1 y’ k = g 0 x’’ g 1 y’’ c = ur. m = v. m ; f = er kr (Way 2) m = c/v pk= (G, o, q, g 0, g 1, u, e, k), sk = (x, y, x’, y’, x’’, y’’) (h 0, h 1 , c, f) Does above help? Proof: u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S - (2) k = g 0 T = (g 0 x’’ g 1 y’’) = g 0 x’’ +αy’’ - (1) f* = g 0 S* = (h 0 x’+x’’ h 1 y’+y’’) = g 0 r(x’+x’’) +r’α(y’ + y’’) x’’ +αy’’ = T - (3) r(x’ + x’’) + r’α(y’ + y’’) = S* - (4) From (2), (3) & (4), Au can compute (x’ + x’’) and (y’ + y’’) and that’s enough to make an illegal DQ in postchallenge phase and still pass the verification and get m and discover (x, y). Adding more variable in the above way does not help. D Random (x, y, x’, y’) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ c= f= h 0 x h 1 y. h 0 x’ h 1 y’ mb pk = (G, o, q, g 0, g 1, u, e, k) m 0, m 1 , |m 0| = |m 1| (h*0, h*1 , c*, f*) Au

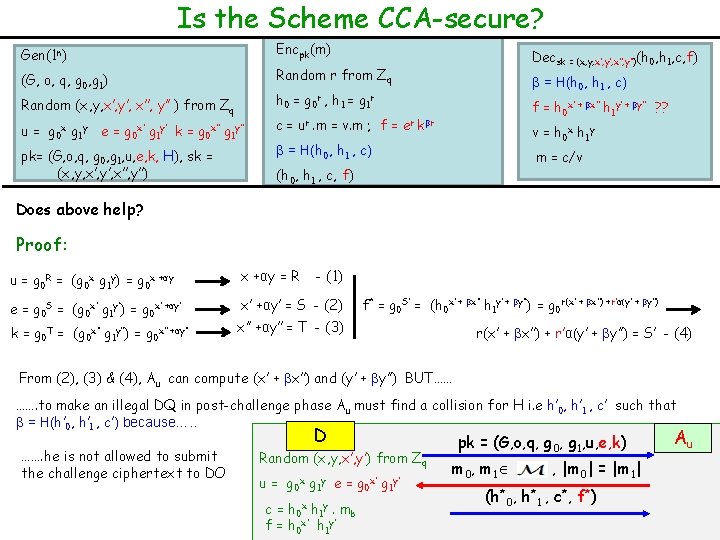
Is the Scheme CCA-secure? Gen(1 n) Encpk(m) (G, o, q, g 0, g 1) Random r from Zq β = H(h 0, h 1 , c) h 0 = g 0 r , h 1 = g 1 r Random (x, y, x’, y’, x’’, y’’ ) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ k = g 0 x’’ g 1 y’’ pk= (G, o, q, g 0, g 1, u, e, k, H), sk = (x, y, x’, y’, x’’, y’’) Decsk = (x, y, x’, y’, x’’, y’’)(h 0, h 1, c, f) f = h 0 x’ + βx’’ h 1 y’ + βy’’ ? ? c = ur. m = v. m ; f = er kβr v = h 0 x h 1 y β = H(h 0, h 1 , c) m = c/v (h 0, h 1 , c, f) Does above help? Proof: u = g 0 R = (g 0 x g 1 y) = g 0 x +αy = R e = g 0 S = (g 0 x’ g 1 y’) = g 0 x’ +αy’ = S - (2) k = g 0 T = (g 0 x’’ g 1 y’’) = g 0 x’’ +αy’’ - (1) f* = g 0 S’ = (h 0 x’ + βx’’ h 1 y’ + βy’’) = g 0 r(x’ + βx’’) +r’α(y’ + βy’’) x’’ +αy’’ = T - (3) r(x’ + βx’’) + r’α(y’ + βy’’) = S’ - (4) From (2), (3) & (4), Au can compute (x’ + βx’’) and (y’ + βy’’) BUT…… ……. to make an illegal DQ in post-challenge phase A u must find a collision for H i. e h’ 0, h’ 1 , c’ such that β = H(h’ 0, h’ 1 , c’) because…. . ……. he is not allowed to submit the challenge ciphertext to DO D Random (x, y, x’, y’) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ c= f= h 0 x h 1 y. h 0 x’ h 1 y’ mb pk = (G, o, q, g 0, g 1, u, e, k) m 0, m 1 , |m 0| = |m 1| (h*0, h*1 , c*, f*) Au

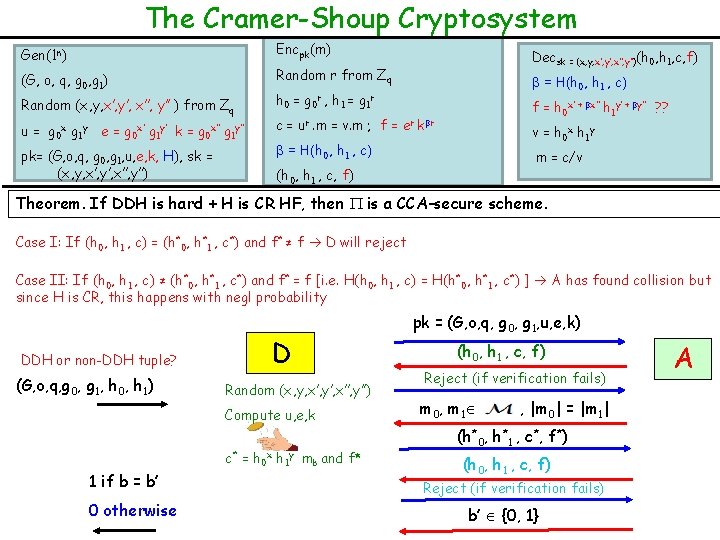
The Cramer-Shoup Cryptosystem Gen(1 n) Encpk(m) (G, o, q, g 0, g 1) Random r from Zq Random (x, y, x’, y’, x’’, y’’ ) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ k = g 0 x’’ g 1 y’’ pk= (G, o, q, g 0, g 1, u, e, k, H), sk = (x, y, x’, y’, x’’, y’’) Decsk = (x, y, x’, y’, x’’, y’’)(h 0, h 1, c, f) β = H(h 0, h 1 , c) h 0 = g 0 r , h 1 = g 1 r f = h 0 x’ + βx’’ h 1 y’ + βy’’ ? ? c = ur. m = v. m ; f = er kβr v = h 0 x h 1 y β = H(h 0, h 1 , c) m = c/v (h 0, h 1 , c, f) Theorem. If DDH is hard + H is CR HF, then is a CCA-secure scheme. Case I: If (h 0, h 1 , c) = (h*0, h*1 , c*) and f* ≠ f D will reject Case II: If (h 0, h 1 , c) ≠ (h*0, h*1 , c*) and f* = f [i. e. H(h 0, h 1 , c) = H(h*0, h*1 , c*) ] A has found collision but since H is CR, this happens with negl probability DDH or non-DDH tuple? (G, o, q, g 0, g 1, h 0, h 1) D Random (x, y, x’, y’, x’’, y’’) Compute u, e, k c* = h 0 x h 1 y mb and f* 1 if b = b’ 0 otherwise pk = (G, o, q, g 0, g 1, u, e, k) (h 0, h 1 , c, f) Reject (if verification fails) m 0, m 1 , |m 0| = |m 1| (h*0, h*1 , c*, f*) (h 0, h 1 , c, f) Reject (if verification fails) b’ {0, 1} A

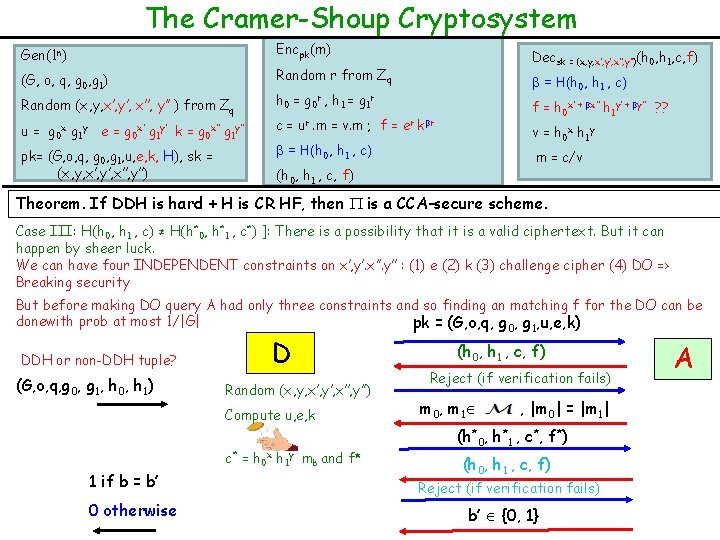
The Cramer-Shoup Cryptosystem Gen(1 n) Encpk(m) (G, o, q, g 0, g 1) Random r from Zq Random (x, y, x’, y’, x’’, y’’ ) from Zq u = g 0 x g 1 y e = g 0 x’ g 1 y’ k = g 0 x’’ g 1 y’’ pk= (G, o, q, g 0, g 1, u, e, k, H), sk = (x, y, x’, y’, x’’, y’’) Decsk = (x, y, x’, y’, x’’, y’’)(h 0, h 1, c, f) β = H(h 0, h 1 , c) h 0 = g 0 r , h 1 = g 1 r f = h 0 x’ + βx’’ h 1 y’ + βy’’ ? ? c = ur. m = v. m ; f = er kβr v = h 0 x h 1 y β = H(h 0, h 1 , c) m = c/v (h 0, h 1 , c, f) Theorem. If DDH is hard + H is CR HF, then is a CCA-secure scheme. Case III: H(h 0, h 1 , c) ≠ H(h*0, h*1 , c*) ]: There is a possibility that it is a valid ciphertext. But it can happen by sheer luck. We can have four INDEPENDENT constraints on x’, y’. x’’. y’’ : (1) e (2) k (3) challenge cipher (4) DO => Breaking security But before making DO query A had only three constraints and so finding an matching f for the DO can be donewith prob at most 1/|G| pk = (G, o, q, g 0, g 1, u, e, k) DDH or non-DDH tuple? (G, o, q, g 0, g 1, h 0, h 1) D Random (x, y, x’, y’, x’’, y’’) Compute u, e, k c* = h 0 x h 1 y mb and f* 1 if b = b’ 0 otherwise (h 0, h 1 , c, f) Reject (if verification fails) m 0, m 1 , |m 0| = |m 1| (h*0, h*1 , c*, f*) (h 0, h 1 , c, f) Reject (if verification fails) b’ {0, 1} A

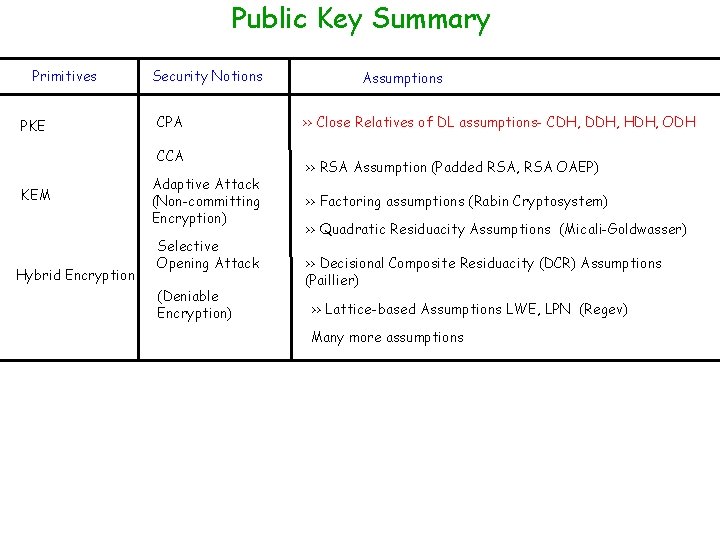
Public Key Summary Primitives PKE Security Notions CPA CCA KEM Hybrid Encryption Adaptive Attack (Non-committing Encryption) Selective Opening Attack (Deniable Encryption) Assumptions >> Close Relatives of DL assumptions- CDH, DDH, HDH, ODH >> RSA Assumption (Padded RSA, RSA OAEP) >> Factoring assumptions (Rabin Cryptosystem) >> Quadratic Residuacity Assumptions (Micali-Goldwasser) >> Decisional Composite Residuacity (DCR) Assumptions (Paillier) >> Lattice-based Assumptions LWE, LPN (Regev) Many more assumptions