Covering Graphs Motivation Suppose you are taken to


















![Computing Minimal Valence Refinement • Let r[u, B] denote the number of edges linking Computing Minimal Valence Refinement • Let r[u, B] denote the number of edges linking](https://slidetodoc.com/presentation_image/270ab20acf8e3925a82e4844671c8b8a/image-37.jpg)
















- Slides: 59

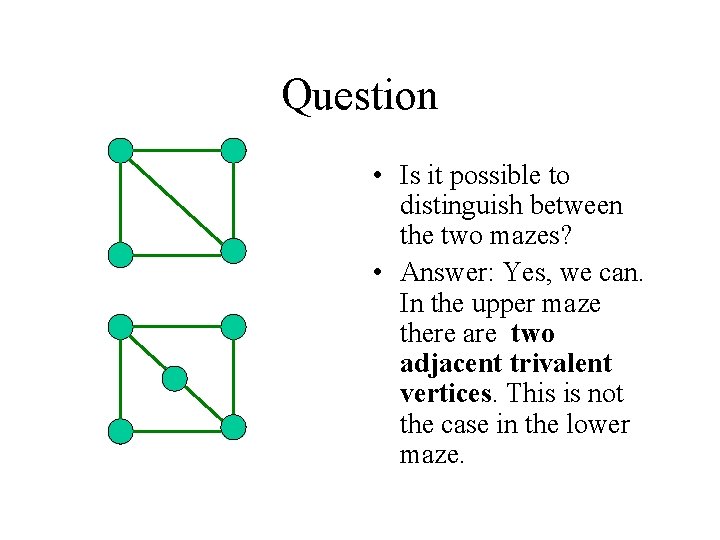
Covering Graphs • Motivation: • Suppose you are taken to two different labyrinths. Is it possible to tell they are distinct just by walking around? • Let us call the first graph maze X, and the second one Y.

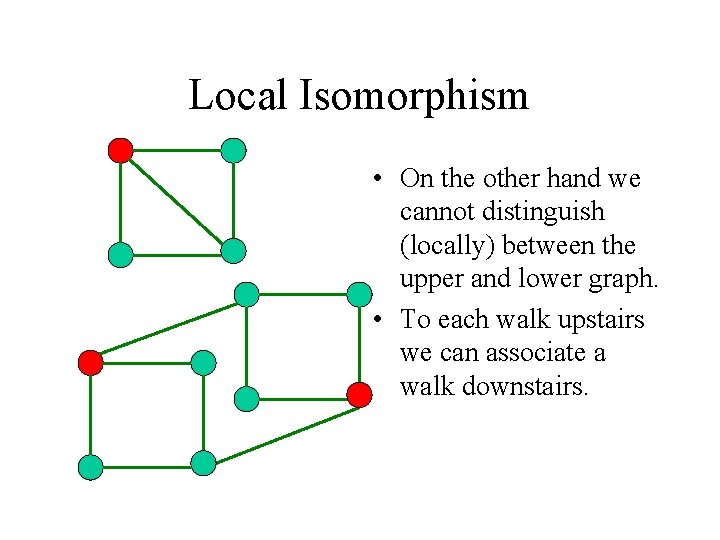
Question • Is it possible to distinguish between the two mazes? • Answer: Yes, we can. In the upper maze there are two adjacent trivalent vertices. This is not the case in the lower maze.

Local Isomorphism • On the other hand we cannot distinguish (locally) between the upper and lower graph. • To each walk upstairs we can associate a walk downstairs.

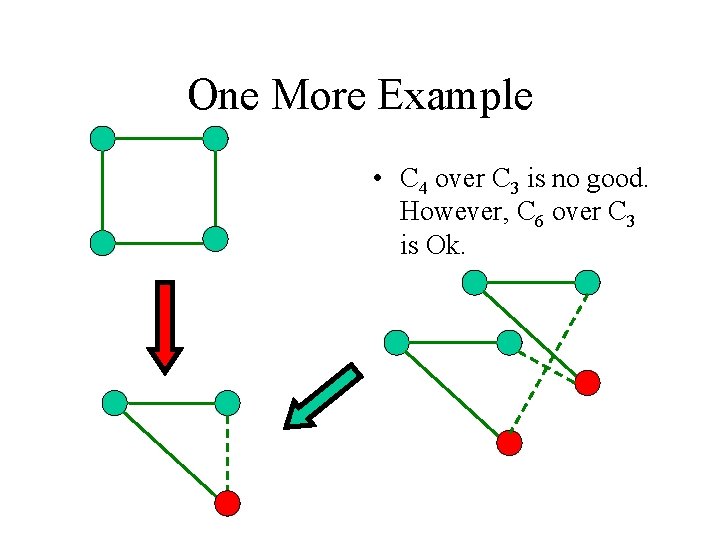
One More Example • C 4 over C 3 is no good. However, C 6 over C 3 is Ok.

Fibers and Sheets. • We say that C 6 is a twosheeted cover C 3. Red vertices are in the same fiber. Similarly, the dotted lines belong to the saem fiber. • Graph mapping f: C 6 C 3 is called covering projection. • Preimage of a vertex f-1(v) (or an edge f-1(e)) is called a fiber. • The cardinality of a fiber is constant. k =|f-1(v)| is called the number of sheets.

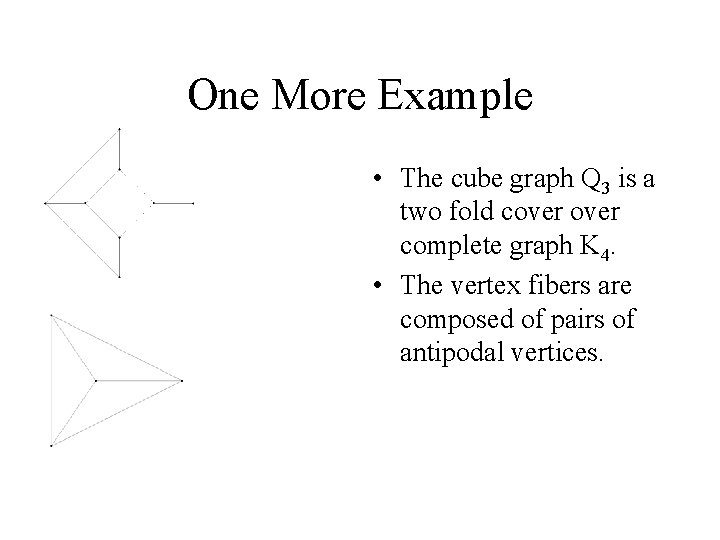
One More Example • The cube graph Q 3 is a two fold cover complete graph K 4. • The vertex fibers are composed of pairs of antipodal vertices.

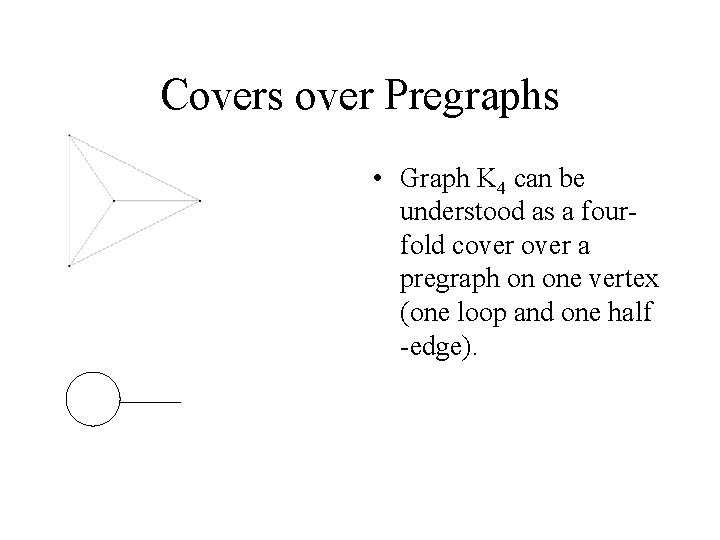
Covers over Pregraphs • Graph K 4 can be understood as a fourfold cover a pregraph on one vertex (one loop and one half -edge).

Voltage Graphs • X = (V, S, i, r) – connected (pre)graph. • ( , A) – permutation group acting on space A. • : S – voltage assignment. • Condition: for each s 2 S we have [s] [r(s)] = id.

Voltage Graph Determines a Covering Graph • Each voltage graph (X, , A, ) determines a covering graph Y and the covering projection f: Y X as follows: • Covering graph Y = (V(Y), S(Y), i, r) • • V(Y) : = V(X) x A S(Y) : = S(X) x A i: S(Y) V(Y): i(s, a) : = (i(s), a). r: S(Y): r(s, a) : = (r(s), [s](a)). • Covering projection f • f: V(Y) V(X): f(x, a) : = x. • f: S(Y) S(X): f(s, a) : = s. • Sometimes we denote the covering graph Y by Cov(X; ).

(Rhetorical) Questions • “Different” voltage graphs may give rise to the “same” cover. What does it mean the “same” and how do we obtain all “different” voltage graphs? • The voltage graph is determined in essence by the abstract group. What is the role of permutation group? • How do we ensure that if X is connected then Y is connected, too?

Kronecker Cover • Let X be a graph. The canonical double cover or Kronecker cover: KC(X) is a twofold cover that is defined by a voltage graph that has nontrivial voltage from Z 2 on each of its edges. It can also be described as the tensor product KC(X) = X £ K 2.

Homework • H 1: Prove that Kronecker cover is bipartite. • H 2: Prove that generalized Petersen graph G(10, 2) is a twofold cover the Petersen graph G(5, 2). • H 3: Determine the Kronecker cover G(5, 2). • H 4: Determine a Zn covering over the handcuff graph G(1, 1), that is not a generalized Petersen graph G(n, r).

Regular Covers • Let Y be a cover X. We are interested in fiber preserving elements of Aut Y (covering transformations). • Let Aut(Y, X) · Aut Y be the group of covering transformations. • The cover Y is regular, if Aut(Y, X) acts transitively on each fiber. • Regular covers are denoted by voltage graphs, where permutation group ( , A) acts regularly on itself by left or right translations: ( , ).

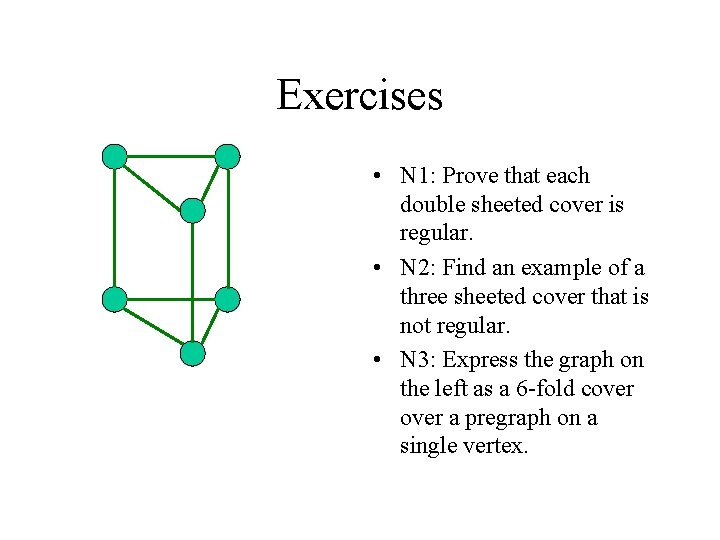
Exercises • N 1: Prove that each double sheeted cover is regular. • N 2: Find an example of a three sheeted cover that is not regular. • N 3: Express the graph on the left as a 6 -fold cover a pregraph on a single vertex.

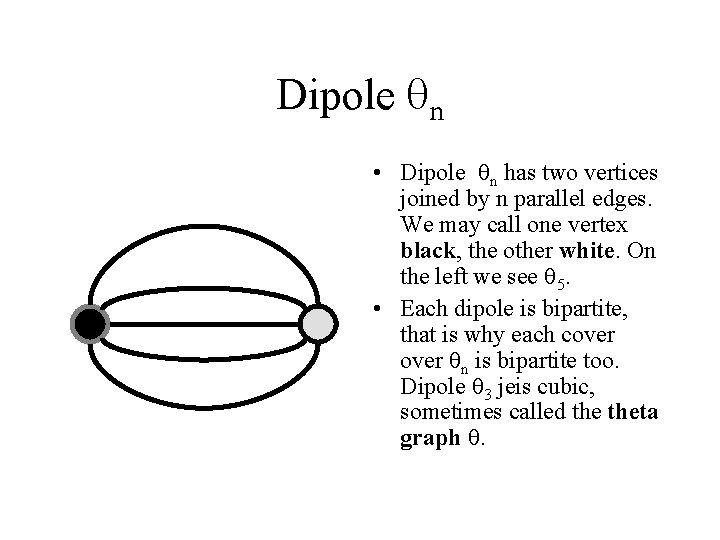
Dipole n • Dipole n has two vertices joined by n parallel edges. We may call one vertex black, the other white. On the left we see 5. • Each dipole is bipartite, that is why each cover n is bipartite too. Dipole 3 jeis cubic, sometimes called theta graph .

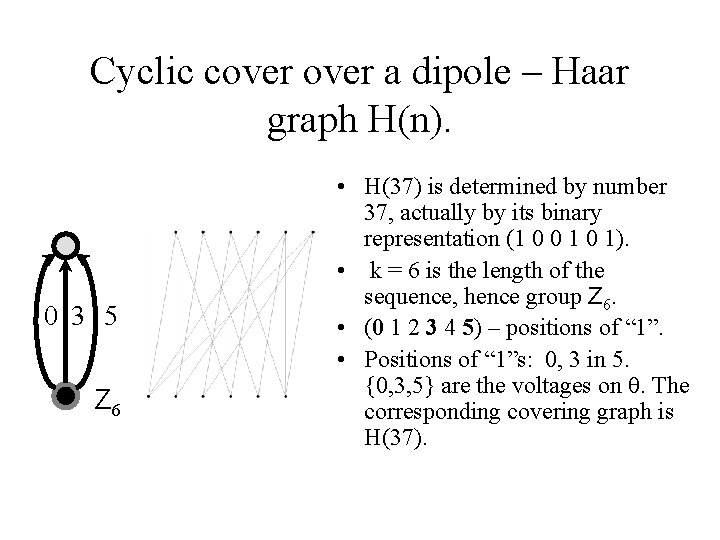
Cyclic cover a dipole – Haar graph H(n). 0 3 5 Z 6 • H(37) is determined by number 37, actually by its binary representation (1 0 0 1). • k = 6 is the length of the sequence, hence group Z 6. • (0 1 2 3 4 5) – positions of “ 1”. • Positions of “ 1”s: 0, 3 in 5. {0, 3, 5} are the voltages on . The corresponding covering graph is H(37).

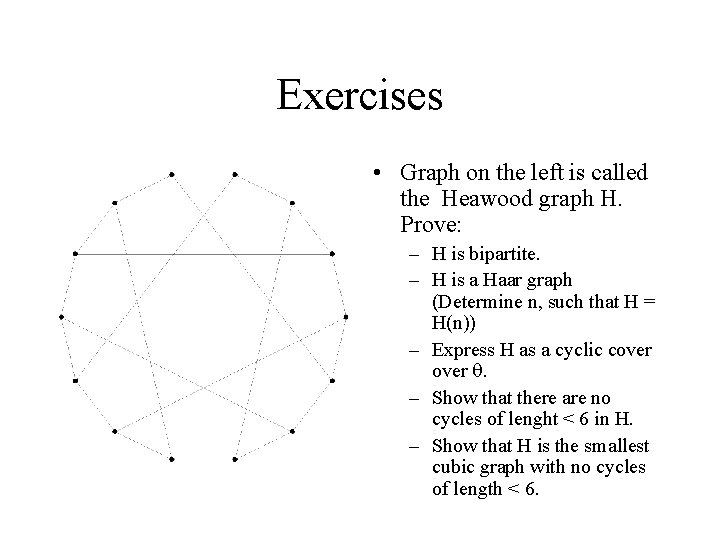
Exercises • Graph on the left is called the Heawood graph H. Prove: – H is bipartite. – H is a Haar graph (Determine n, such that H = H(n)) – Express H as a cyclic cover . – Show that there are no cycles of lenght < 6 in H. – Show that H is the smallest cubic graph with no cycles of length < 6.

Cages as Covering Graphs • A g-cage is a cubic graph of girth g that has the least number of vertices. • Small cages can be readily described as covering graphs.

1 -Cage • Usually we consider only simple graphs. For our purposes it makes sense to define also a 1 -cage as a pregraph on the left. • 1 -cage is the unique smallest cubic pregraph.

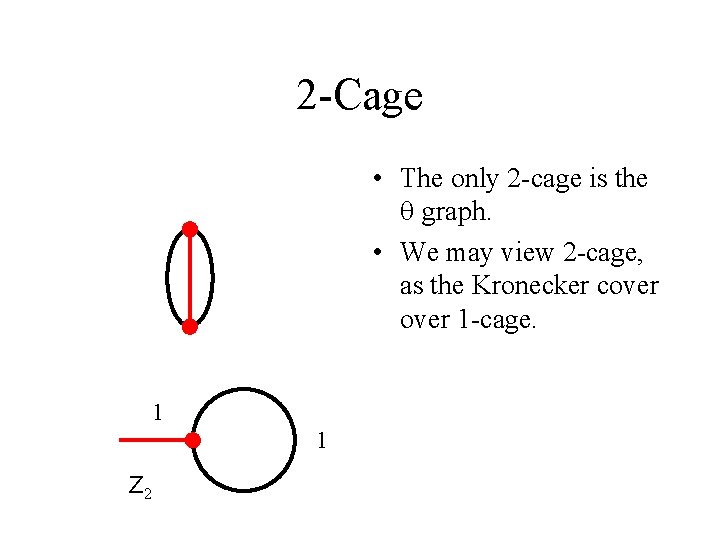
2 -Cage • The only 2 -cage is the graph. • We may view 2 -cage, as the Kronecker cover 1 -cage. 1 1 Z 2

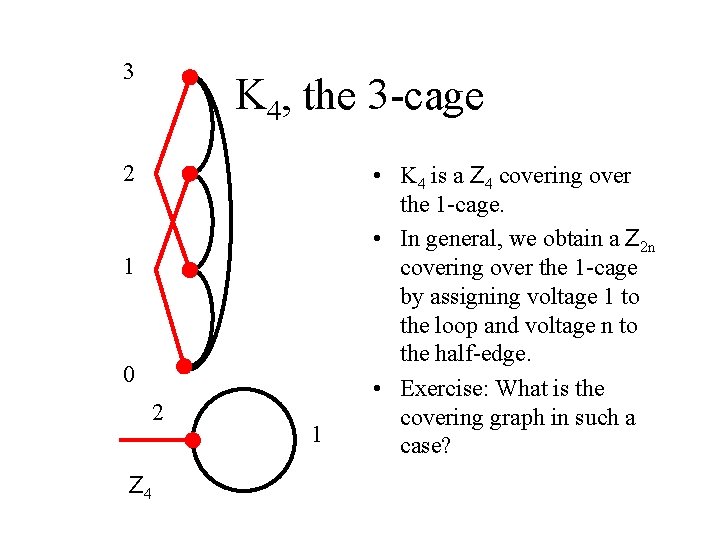
3 K 4, the 3 -cage 2 1 0 2 Z 4 1 • K 4 is a Z 4 covering over the 1 -cage. • In general, we obtain a Z 2 n covering over the 1 -cage by assigning voltage 1 to the loop and voltage n to the half-edge. • Exercise: What is the covering graph in such a case?

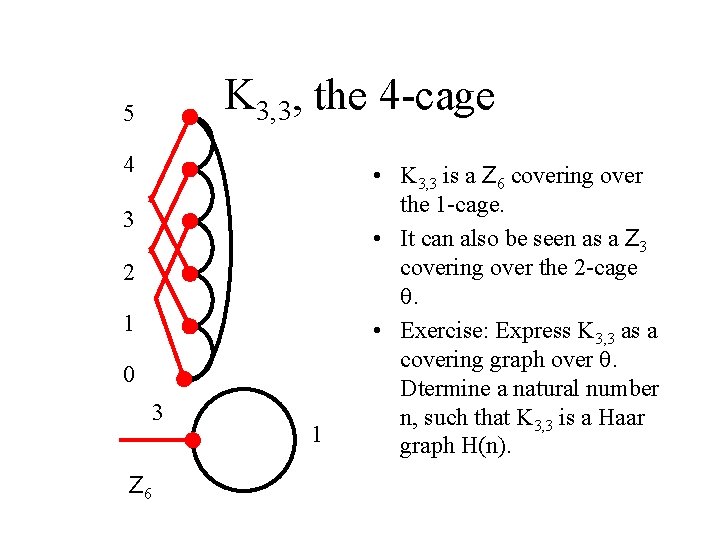
K 3, 3, the 4 -cage 5 4 3 2 1 0 3 Z 6 1 • K 3, 3 is a Z 6 covering over the 1 -cage. • It can also be seen as a Z 3 covering over the 2 -cage . • Exercise: Express K 3, 3 as a covering graph over . Dtermine a natural number n, such that K 3, 3 is a Haar graph H(n).

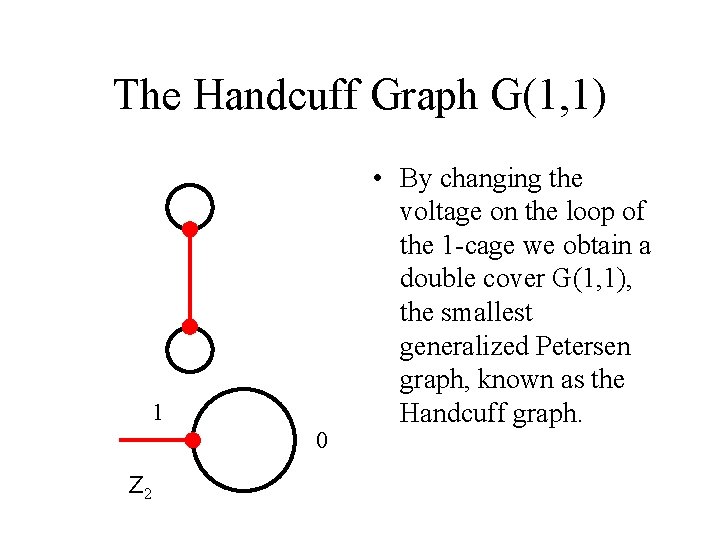
The Handcuff Graph G(1, 1) 1 0 Z 2 • By changing the voltage on the loop of the 1 -cage we obtain a double cover G(1, 1), the smallest generalized Petersen graph, known as the Handcuff graph.

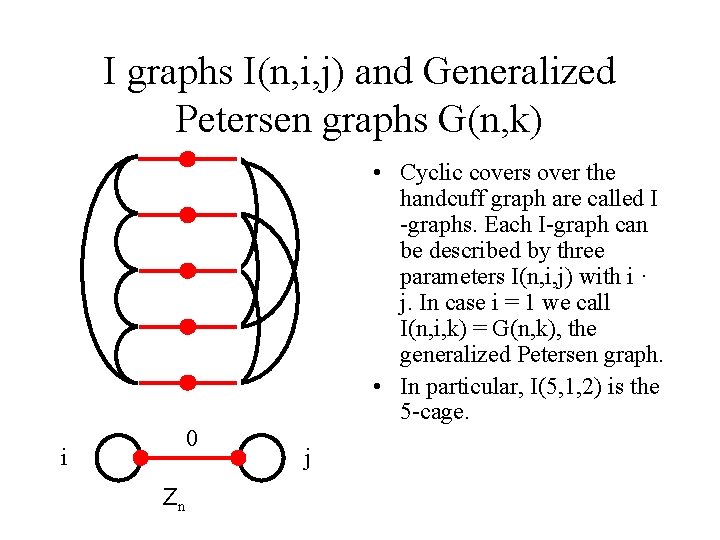
I graphs I(n, i, j) and Generalized Petersen graphs G(n, k) 0 i Zn • Cyclic covers over the handcuff graph are called I -graphs. Each I-graph can be described by three parameters I(n, i, j) with i · j. In case i = 1 we call I(n, i, k) = G(n, k), the generalized Petersen graph. • In particular, I(5, 1, 2) is the 5 -cage. j

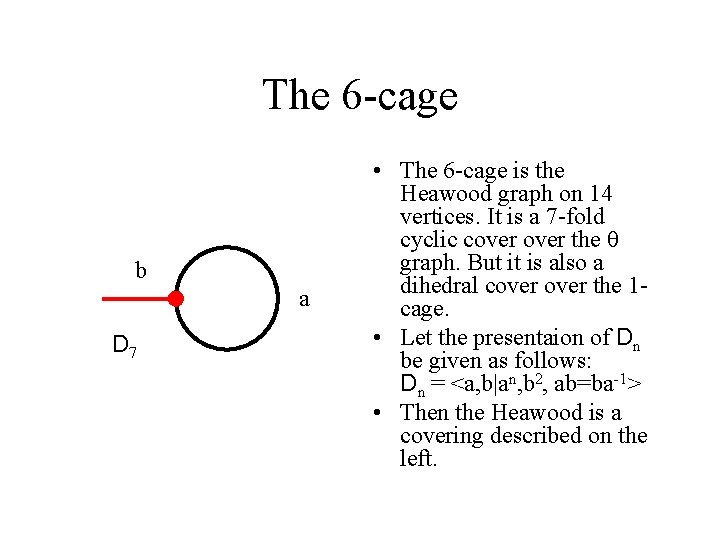
The 6 -cage b a D 7 • The 6 -cage is the Heawood graph on 14 vertices. It is a 7 -fold cyclic cover the graph. But it is also a dihedral cover the 1 cage. • Let the presentaion of Dn be given as follows: Dn = <a, b|an, b 2, ab=ba-1> • Then the Heawood is a covering described on the left.

Exercises • N 1. Express the 7 -cage as a covering graph. • N 2. Express the 8 -cage as a covering graph.

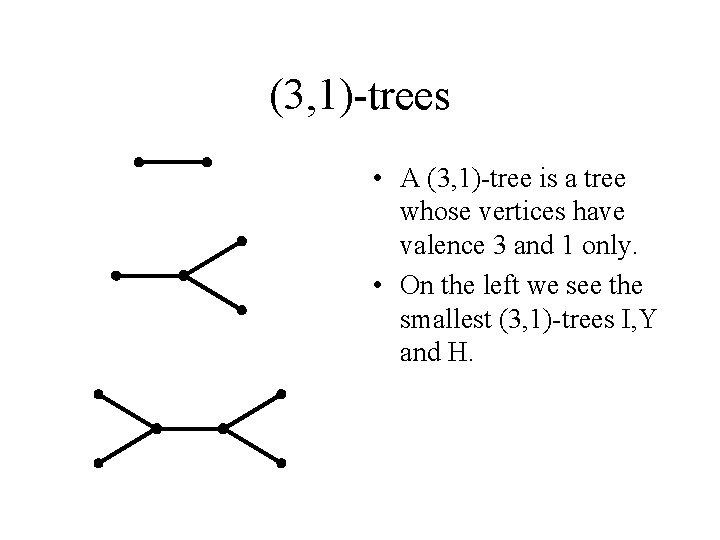
(3, 1)-trees • A (3, 1)-tree is a tree whose vertices have valence 3 and 1 only. • On the left we see the smallest (3, 1)-trees I, Y and H.

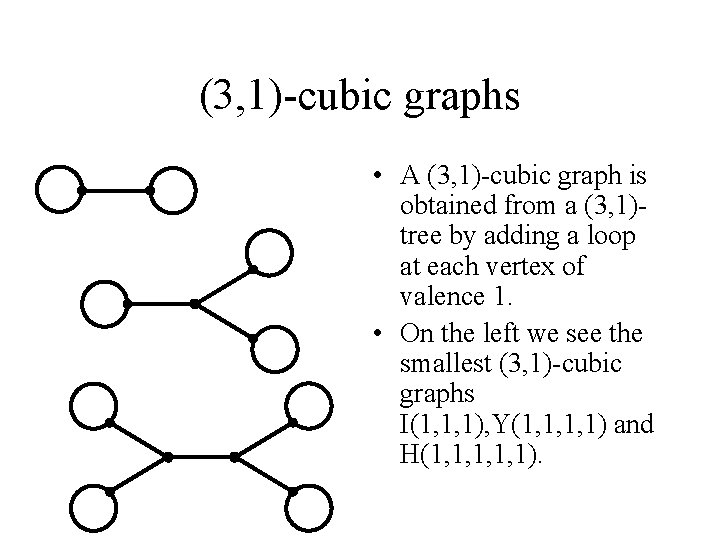
(3, 1)-cubic graphs • A (3, 1)-cubic graph is obtained from a (3, 1)tree by adding a loop at each vertex of valence 1. • On the left we see the smallest (3, 1)-cubic graphs I(1, 1, 1), Y(1, 1, 1, 1) and H(1, 1, 1).

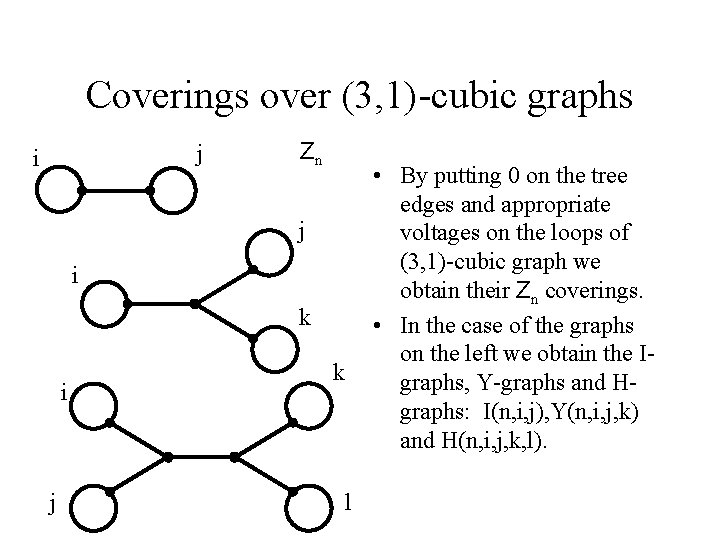
Coverings over (3, 1)-cubic graphs j i Zn j i k i j k l • By putting 0 on the tree edges and appropriate voltages on the loops of (3, 1)-cubic graph we obtain their Zn coverings. • In the case of the graphs on the left we obtain the Igraphs, Y-graphs and Hgraphs: I(n, i, j), Y(n, i, j, k) and H(n, i, j, k, l).

Covers Determined by Graphs • We know already that there exists a cover, namely Kronecker cover, that depends only on X itself and the voltage assignment plays a minor role. • Now we will present some covers that have a similar property.

Coverings and Trees • Let X be a connected graph and let Cov(X) denote all connected covers over X: • Cov(X) = {(Y, )| Y connected and : Y ! X, covering projection}. For each connected X we have (X, id) 2 Cov(X). • Proposition: For a connected X we have Cov(X) = {(X, id)} if and only if X is a tree. • This fact holds both for finite and locally finite trees.

Universal cover • • Let X, Y and Z be connected graphs and let : Y ! X and : Z ! Y be covering projections. On the other hand, we may consider the class Cov(X) of all coverings over X. We may introduce a partial order in Cov(X). (Y, ) < (Z, ) if there exists a covering projection (Z, ) 2 Cov(Y) so that = . Proposition: Any connected finite or locally finite graph X can be covered by some tree T; : T ! X. Proposition: Any connected finite or locally finite graph X can be covered by at most one tree T. Proposition: Let : T ! X be a covering projection form a tree to a connected graph X. Then for each covering : Y ! X there exists a covering : T ! Y such that = . Corollary: For each connected X the poset Cov(X) has a maximal element (T, ) where T is a tree. The maximal element (T, ) 2 Cov(X) is called the universal covering of X.

Construction of Universal Cover • There is a simple construction of the universal covering projection. • Let X be a connected graph and let T µ X be a spanning tree. Furthermore, let S = E(G) E(T) be the set of edges not in tree T. • Consider S to be the set of generators for a free group F(S) and F(S) to be the voltage group. • Let us assing voltages on E(G) as follows: • If e 2 E(T) the voltage on e is identity. • If e 2 S the voltage is the corresponding generator (or its inverse) • Note: The construction does not depend on the choice of direction of edges. • Proposition: The described construction gives rise to the universal cover.

Examples • Example: The universal cover any regular k-valent graph is a regular infinte tree T(1, k).

Valence Partition and Valence Refinement • Let G be a graph and let B = {B 1, . . . , Bk} be a partition of its vertex set V(G) for which there are constants rij, 1 · i, j · k such that for each v 2 Bi there are rij edges linking v to the vertices in Bj. Let R = [rij] be the corresponding k £ k matrix, Then B is called valence partition and R is called valence refinement. If k is minimal, then B is called minimal valence partition and R is called minimal valence refinement. • Two refinements R and R’ are considered the same if one can be transformed to the other one by simultaneous permutation of rows and columns. • A refinement is uniform, if each row is constant.

Construction • • • Given graphs G and G’ with a common refinement. Let mij denote the number of arcs in G of type i ! j. Let ni denote the number of vertices in G of type i. Let bij = lcm(mij)/mij. (If mij = 0 , let bij undefined). Let ai = lcm(mij)/ni. Note that bij and ai depend only on the common matrix R and are the same for both graphs G and G’. Let l(e) or l(e’) be a linear order given to all type i ! j arcs with a common initial vertex i(e) (or i(e’)). Let V(H) = {(i, v, v’, p)|v and v’ of type i, p 2 Zai} Let S(H) = {(i, j, e, e’, q)|e and e’ of type i ! j, q 2 Zbij} r(i, j, e, e’, q) : = (j, i, r(e), r(e’), q) i(i, j, e, e’, q) : = (i, i(e), i(e’), q rij + l(e)-l(e’)} H is a common cover of G and G’.
![Computing Minimal Valence Refinement Let ru B denote the number of edges linking Computing Minimal Valence Refinement • Let r[u, B] denote the number of edges linking](https://slidetodoc.com/presentation_image/270ab20acf8e3925a82e4844671c8b8a/image-37.jpg)
Computing Minimal Valence Refinement • Let r[u, B] denote the number of edges linking u to the vertices in B. • Algorithm [F. T. Leighton, Finite Common Coverings of Graphs, JCT(B) 33 1982, 231 -238. ] • Step 1. Place two vertices in the same block if and only if they have the same valence. • Step 2. While there exist two blocks B and B’ and two distinct vertices u, v in B with r[u, B’] r[v, B’] repeat the following: • Partition the block B into subblocks in such a way that two vertices u, b of B remain in the same block if and only if r[u, B’] = r[v, B’] for each B’ of the previous partition. • Step 3. From minimal valence partition B compute the minimal vertex refinement R. • Note: We may maintain R during the run of the algorithm as a matrix whose elements are sets of numbers.

Comon Cover • 1. 2. 3. 4. 5. • Theorem. Given any two finite graphs G and H, the following statements are equivalent: G and H have the same universal cover, G and H have a common finite cover, G and H have a common cover, G and H have the same minimal valence refinement. G and H have the same some valence refinement. Homework. Find the result in the literature and construct a finite comon cover of G(5, 2) and G(6, 2).

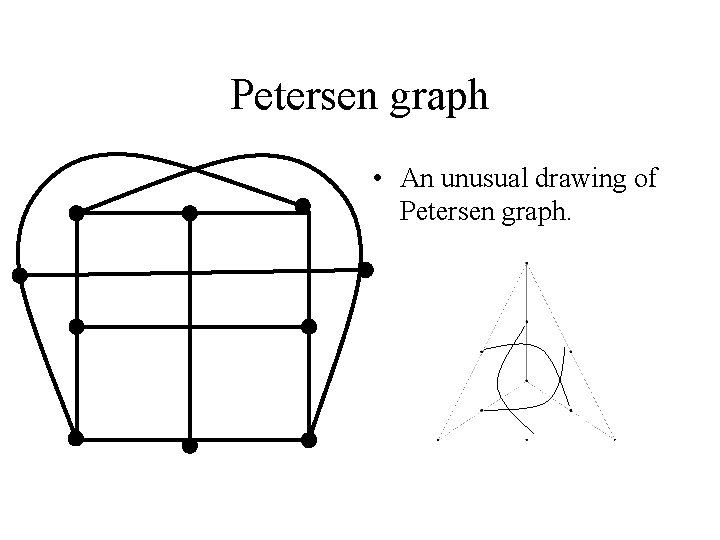
Petersen graph • An unusual drawing of Petersen graph.

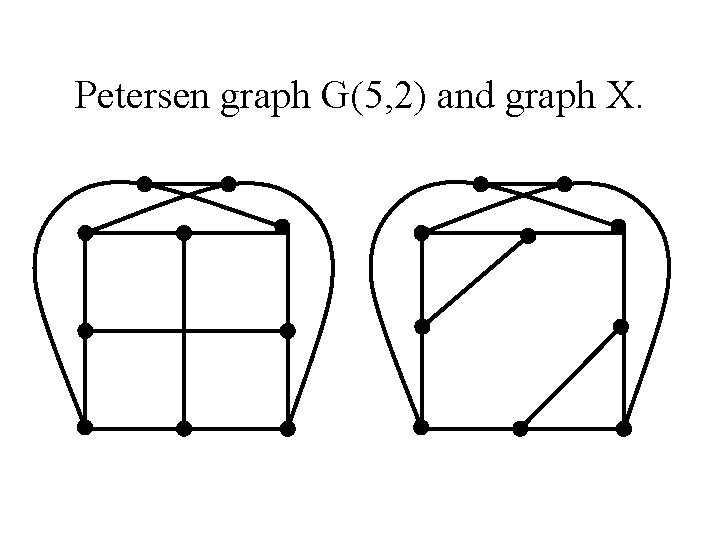
Petersen graph G(5, 2) and graph X.

Kronecker Cover - Revisited • Kronecker cover KC(G) is an example of covers, determined by the graph itself. • Exercise. Show that G(5, 2) and X have the same Kronecker cover.

THE covering graph • Let G be a graph with the vertex set V. By THE(G) we denote the following covering graph. • To each edge e = uv we assing transposition e = (u, v) 2 Sym(V). The resulting covering graph has two components, one being isomorphic to G. The other componet is called THE covering graph.

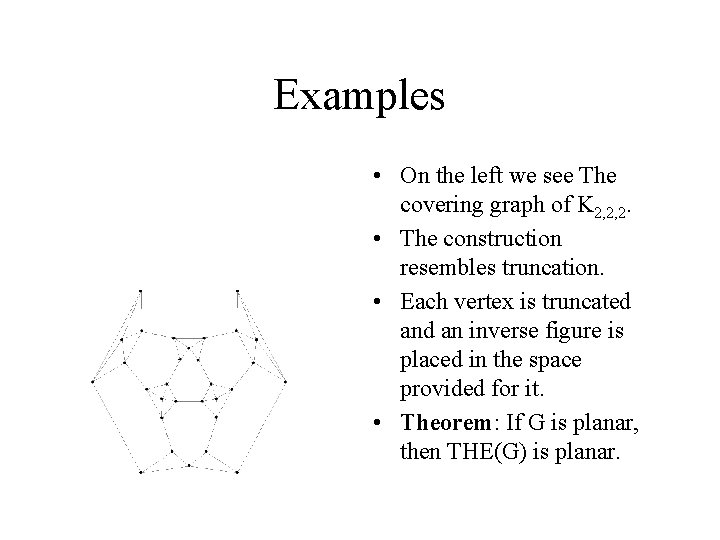
Examples • On the left we see The covering graph of K 2, 2, 2. • The construction resembles truncation. • Each vertex is truncated an inverse figure is placed in the space provided for it. • Theorem: If G is planar, then THE(G) is planar.

Homework • H 1. Given connected graph G with n vertices and e edges and with valence sequence (d 1, d 2, . . . , dn). Determine the parameters for THE(G). • H 2. Determine all connected graphs G for which girth(G) girth(THE(G)).

The fundamental group of a graph. • Let G be a connected graph rooted at r 2 V(G) and let denote the collection of closed walks rooted at r. • Let and be two closed walks rooted at r. The compositum is also a closed walk rooted at r. • We may also define -1 as the inverse walk. • Finally, we need equality (equivalence). • 1 2 ~ 1 e e-1 2. • (G, r) : = /~ is a group, called the fundamental group of G (first homotopy group). • Fact: (G, r) is a free group generated with m-n+1 generators.

The first Homology group of a graph • Let G be a connected graph and T one of its spanning trees. Each edge h 2 GT of the co-tree defines a unique cycle C(h) µ E(G). • The charactersitic vector h 2 {0, 1}m, h(e) = 1, if e 2 C(h) and h(e) = 0, represents C(h). The set of all charactersitic vectors spans a m-n+1 dimensional Z-module in Zm. This can be also viewed as a free abelian group isomorphic to Zm-n+1. • This group is called the first homology group H 1(G, Z). We may replace Z by Zk and obtain the first Zk homology group Zkm-n+1.

Pseudohomological Covers • Idea: Let G be a graph and T its spanning tree and with the edges H = {h 1, h 2, . . . , hm-n+1} = E(G)E(T). Let (H) be a group with m-n+1 interchangeable generators H. The pseudohomological -cover HOM(G, , T) is determined by a voltage graph with (e) = id, for e 2 E(T) and (h) = h, for h 2 E(G)E(T). • Main Question. Is HOM(G, , T) independent of the choice of T and the selection of the generators or their inverses? If the answer is yes, the covering is called homological cover.

Pseudohomological 2 -cover • Let G be a graph and T its spanning tree. The pseudohomological 2 -cover HOM(G, Z 2, T) is determined by a voltage graph with (e) = 0, for e 2 E(T) and (e) = 1, for e E(T). • Theorem. If G is connected then HOM(G, Z 2, T) is connected if and only if G is not a tree.

Example 0 1 0 0 1 1 Z 2 0 1 0 2 • The two voltage graphs on the left determine different pseudohomological Z 2 covers. • Cov(G, 2) is bipartite and Cov(G, 1) is not.

Switching • Let (G, ) be a voltage graph. Let : V(G) ! be an arbitrary mapping, called switching, that assigns voltages to vertices. Define a new voltage assignment as follows: • (s) : = (i(s)) (s) (i(r(s))-1. • is well-defined. • Namely (r(s)) = (i(r(s))) (r(s)) (i(s))-1. • Hence (r(s))-1 = (i(s)) (r(s))-1 (i(r(s)))-1 = (i(s)) (s) (i(r(s)))-1 = (s). • Clearly for any switching the graphs Cov(G, ) and Cov(G, ) coincide. • Given (G, ) and any spanning tree T. There exists a switching such that the resulting is identity on T. • If, in addition, T is rooted at v, we may select (v) = id (or arbitrarily) and this determines switching completely.

Homological Elementary Abelian Covers • Let G be a graph with a spanning tree T. Let k = m-n+1 be the number of edges in GT. Define the voltage assignment such that each non-tree edge gets the voltage ei = (0, 0, . . , 0, 1, 0, . . . , 0) 2 Zpk. • Claim: If p is prime, then Cov(G, ) is independent of T. • Question: What happens in the case p is not prime?

Tree-To-Tree Switch • Let T and T’ be two spanning trees of G. Let H = {h 1, h 2, . . . , hk} be the co-tree edges of T. Let r be the root of G. For each vertex w 2 V(G) there is a unique path P(T’, w, r) on the three T’ from w to v. Let S(w) µ H be the collection of co-tree edges on this path. Let S(w) be the label given to w. Hence (w) = { hi| hi 2 S(w)}. • Claim: Starting with homological voltage assignment relative to T and applying the tree-to-tree switch , the voltages are given as follows: • The edges on T’ get voltage 0. • An edge e = uv on a co-tree T’ get the voltage: • k(e) = S(u) + S(v) if e 2 T. • k(e) = S(u) + S(v) + h(e) if e T. • Each co-tree edge e defines a cycle C(e). The net voltage on C(e) is equal to k(e). • The voltages k(e), for e T’ span the whole Z 2 k.

Exercises • N 1. Let Znk be an elementary abelian group. Let S be a set of generators with the following property. Each element is a 0 -1 vector. They generate the whole group. • Show that |S| = k. • Show that there is an automorphism of the group mapping S to the standard generating set.

Real Homological Cover (0, 1) (1, 0) Z 2 2 • Let G be a graph with a given cycle basis C 1, C 2, . . . , Ck. Direct each cycle and assign to each edge of Ci the voltage ei 2 Znk. The final voltage assignmnet is given by adding the partial voltages. • An example is given on the left. The cycle basis is determined by a spanning tree.

Least Common Cover • Theorem: There exist finite connected graphs H 1, H 2, G 1, G 2 such that G 1 and G 2 are both double covers of H 1 and H 2. • Proof. We start with graphs G = G(5, 2) and X that we know from earlier.

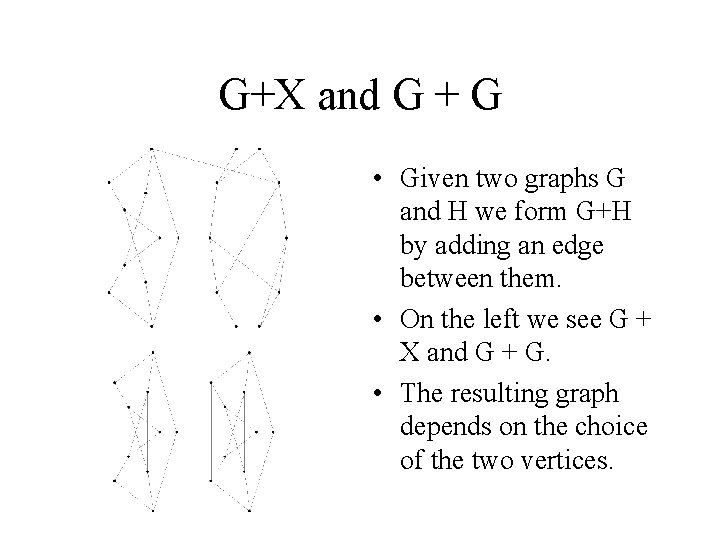
G+X and G + G • Given two graphs G and H we form G+H by adding an edge between them. • On the left we see G + X and G + G. • The resulting graph depends on the choice of the two vertices.

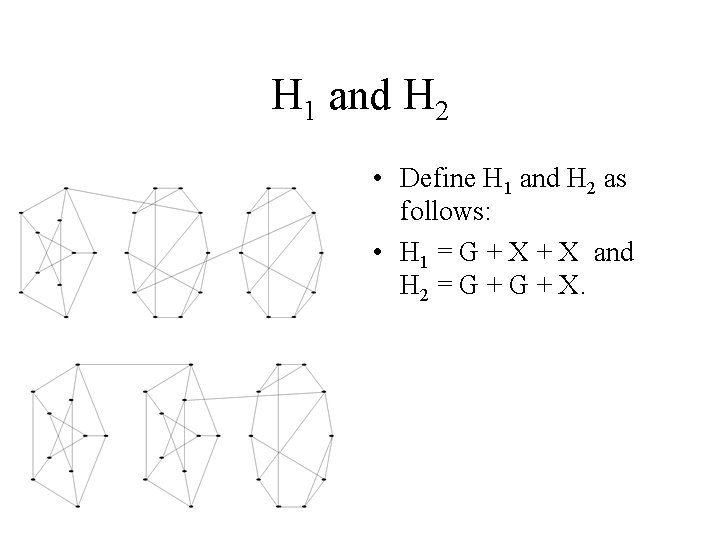
H 1 and H 2 • Define H 1 and H 2 as follows: • H 1 = G + X and H 2 = G + X.

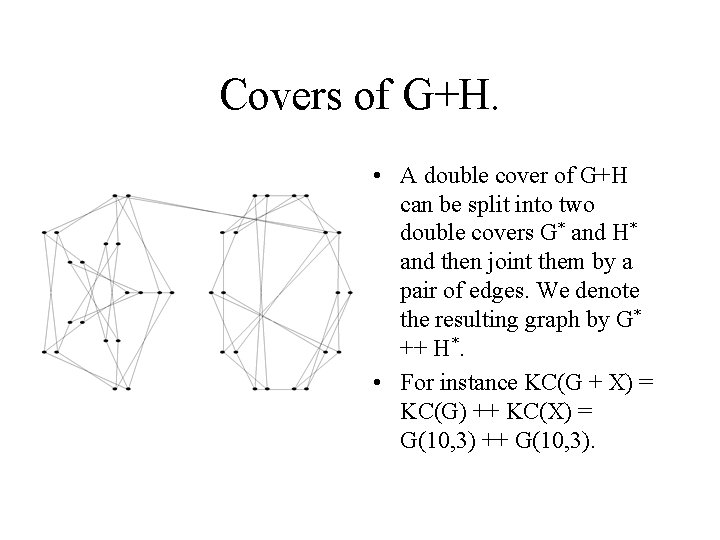
Covers of G+H. • A double cover of G+H can be split into two double covers G* and H* and then joint them by a pair of edges. We denote the resulting graph by G* ++ H*. • For instance KC(G + X) = KC(G) ++ KC(X) = G(10, 3) ++ G(10, 3).

End of Proof • Let G 1 = G(10, 3) ++ G(10, 3) and G 2 = G(10, 3) ++ 2 X. • G 1 and G 2 are distinct. They are both covers of H 1 and H 2.
 Antigentest åre
Antigentest åre Good state and bad state graphs
Good state and bad state graphs Speed and velocity
Speed and velocity Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive End behaviour chart
End behaviour chart What are the 4 types of writing
What are the 4 types of writing The fact that money must withstand the wear and tear
The fact that money must withstand the wear and tear An airplane makes a straight back-and-forth round trip
An airplane makes a straight back-and-forth round trip Suppose you tear open the corner of a bag of m&ms
Suppose you tear open the corner of a bag of m&ms Poe uses several elements of foreshadowing
Poe uses several elements of foreshadowing Suppose you are talking by interplanetary telephone
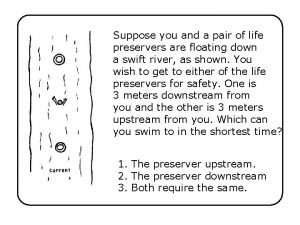
Suppose you are talking by interplanetary telephone You're quite wrong to suppose i shall regret what i did
You're quite wrong to suppose i shall regret what i did Suppose you want to combine two types of fruit drink
Suppose you want to combine two types of fruit drink Suppose q is the midpoint of pr
Suppose q is the midpoint of pr Cigna vitamin d policy
Cigna vitamin d policy Cigna not covering vitamin d testing
Cigna not covering vitamin d testing Continuous pyrolysis plant
Continuous pyrolysis plant Heart membranes
Heart membranes Sequential covering algorithm in data mining
Sequential covering algorithm in data mining What makes hair evidence valuable
What makes hair evidence valuable Placing order letter
Placing order letter Coverings of the brain
Coverings of the brain Thick tough white outer covering eyeball
Thick tough white outer covering eyeball Set covering machine
Set covering machine Signed statement for head covering
Signed statement for head covering Hanging meat as a cargo
Hanging meat as a cargo Dorsal nerve cord
Dorsal nerve cord Whats a covering letter
Whats a covering letter The scale structure covering the exterior of the hair
The scale structure covering the exterior of the hair Inversion of testis
Inversion of testis Covert_tcp
Covert_tcp Cotoderm
Cotoderm Covering letter for resignation
Covering letter for resignation Oolab orthotics
Oolab orthotics A shedding of one or more nails either in whole or in part
A shedding of one or more nails either in whole or in part Costal pleura
Costal pleura Locating tetrahedral and octahedral voids
Locating tetrahedral and octahedral voids Christian headcovering
Christian headcovering Non chordata
Non chordata Outer covering definition
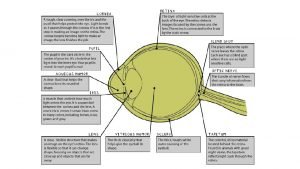
Outer covering definition Thin transparent covering of the eye
Thin transparent covering of the eye Covering of spermatic cord
Covering of spermatic cord What is the gooey liquid in plant and animal cells
What is the gooey liquid in plant and animal cells Floor covering weekly top 50
Floor covering weekly top 50 Tough outer covering of bone
Tough outer covering of bone Do you love rain
Do you love rain You are what you eat do you agree or disagree
You are what you eat do you agree or disagree If you think you can you can poem
If you think you can you can poem Tell me what you eat and i shall tell you what you are
Tell me what you eat and i shall tell you what you are I will follow you follow you wherever
I will follow you follow you wherever When and where was this photograph taken?
When and where was this photograph taken? 22 taken van de brandweer
22 taken van de brandweer If past simple
If past simple The road not taken theme
The road not taken theme Stanza 4 the road not taken
Stanza 4 the road not taken The road not taken hots
The road not taken hots The road not taken figurative language
The road not taken figurative language Swana physical features map
Swana physical features map Where is the apical pulse located
Where is the apical pulse located Rhyme of the road not taken
Rhyme of the road not taken