The covering procedure The covering procedure The covering




























- Slides: 59

The covering procedure

The covering procedure

The covering procedure • Remove rows with essential PI’s and any columns with x’s in those rows

The covering procedure • Remove rows that are covered by other rows • Remove columns that cover other columns • Why?

The covering procedure • Remove rows that are covered by other rows • Remove columns that cover other columns

The covering procedure • Rows PI’s – Covering row takes care of more minterms – Minterms included in a smaller (covered) row are also included in the bigger (covering) one – Can discard the small ones and use only the covering row; minterm coverage is preserved • Columns min/max terms – Whenever a min/max term corresponding to a covered (smaller) column is included by some PI, the min/max term corresponding to the covering (bigger) column also gets included – Covering column can be dropped – Reduces # of PI’s that include this min/max term

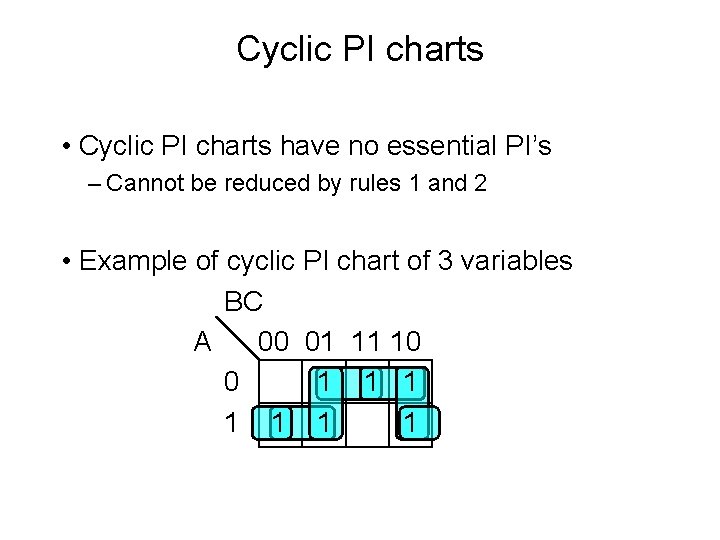
Cyclic PI charts • Cyclic PI charts have no essential PI’s – Cannot be reduced by rules 1 and 2 • Example of cyclic PI chart of 3 variables BC A 00 01 11 10 0 1 1 1 1

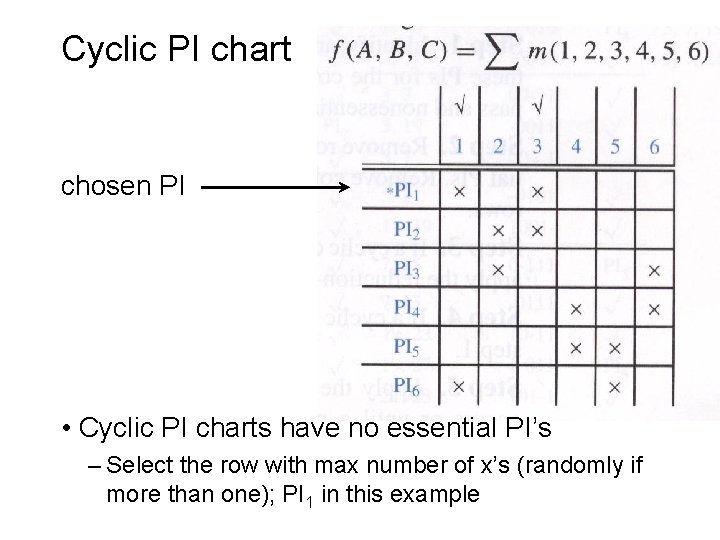
Cyclic PI chart chosen PI • Cyclic PI charts have no essential PI’s – Select the row with max number of x’s (randomly if more than one); PI 1 in this example

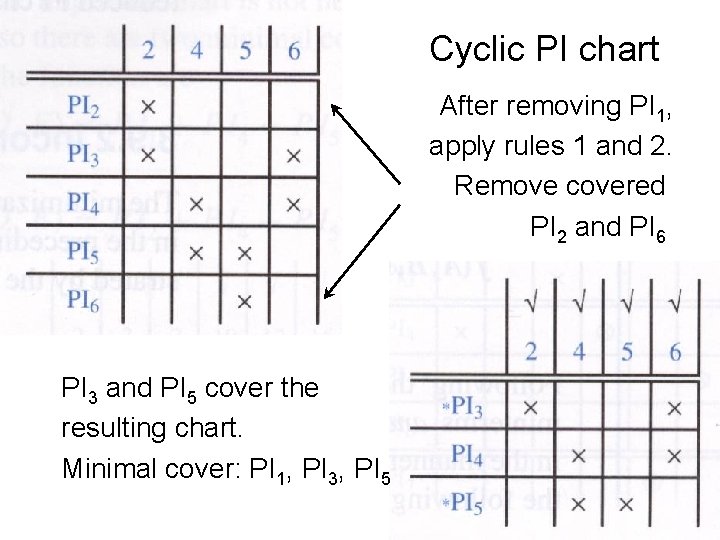
Cyclic PI chart After removing PI 1, apply rules 1 and 2. Remove covered PI 2 and PI 6 PI 3 and PI 5 cover the resulting chart. Minimal cover: PI 1, PI 3, PI 5

Cyclic PI charts • Example of cyclic PI chart of 4 variables 1 1 1 • Q: if PI’s covering 4 minterms are allowed, can one create a cyclic PI chart where no PIs are essential?

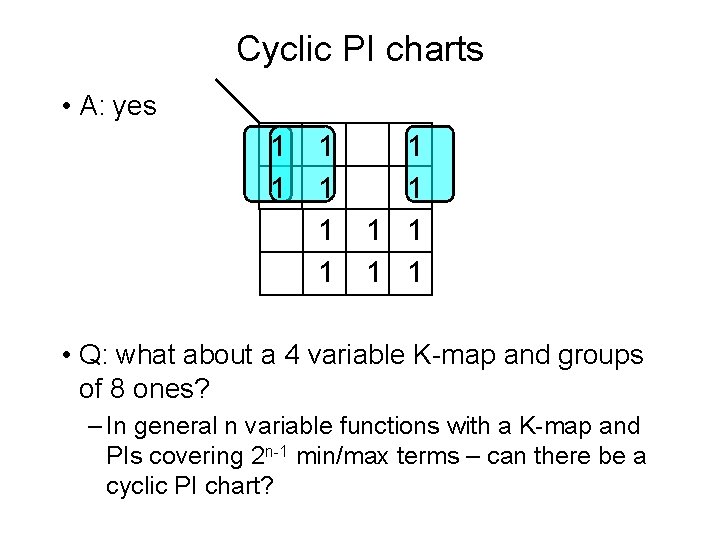
Cyclic PI charts • A: yes 1 1 1 • Q: what about a 4 variable K-map and groups of 8 ones? – In general n variable functions with a K-map and PIs covering 2 n-1 min/max terms – can there be a cyclic PI chart?

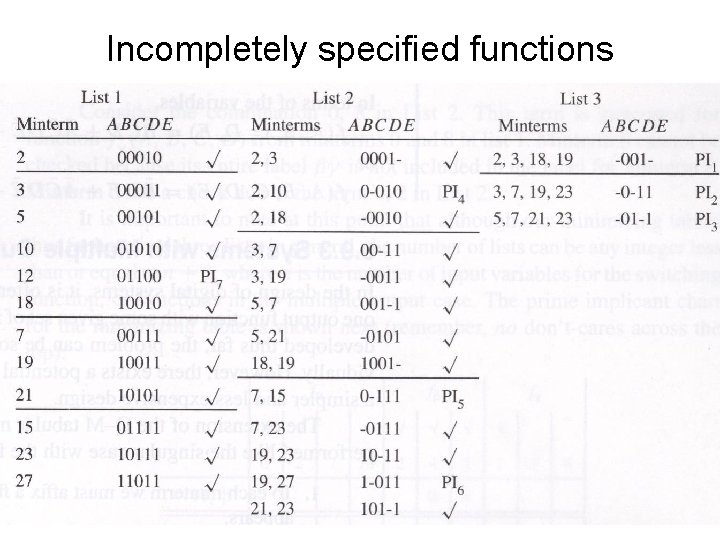
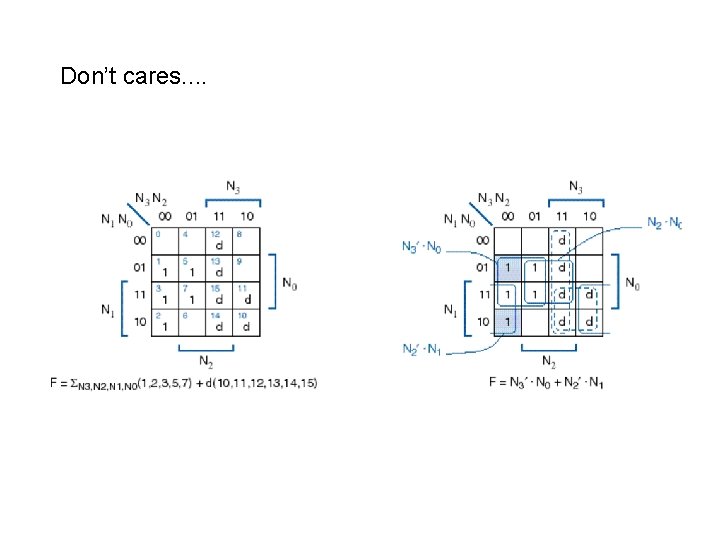
Incompletely specified functions • When some of the minterms can be either 0 or 1, we can denote them by ‘d’ (don’t care) • When simplifying, we use ‘d’s to generate PIs, but do not include them in the PI chart

Incompletely specified functions

Incompletely specified functions

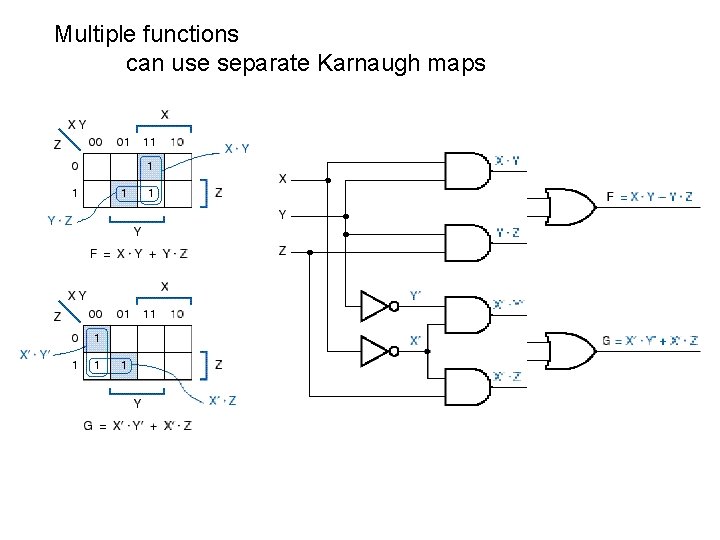
Multiple simultaneous outputs

Multiple simultaneous outputs

Multiple simultaneous outputs • In general, # of lists ≤ n+1 (n = # variables)

‘d’s are not in the charts, but are used for PIs • List 1, group 1 • Group 2, list 2 • Group 3, list 3

Multiple simultaneous outputs Why select PI 3 over PI 11? • PIs from higher-numbered list are likely to cover more PIs (not always true: don’t cares)

Multiple simultaneous outputs

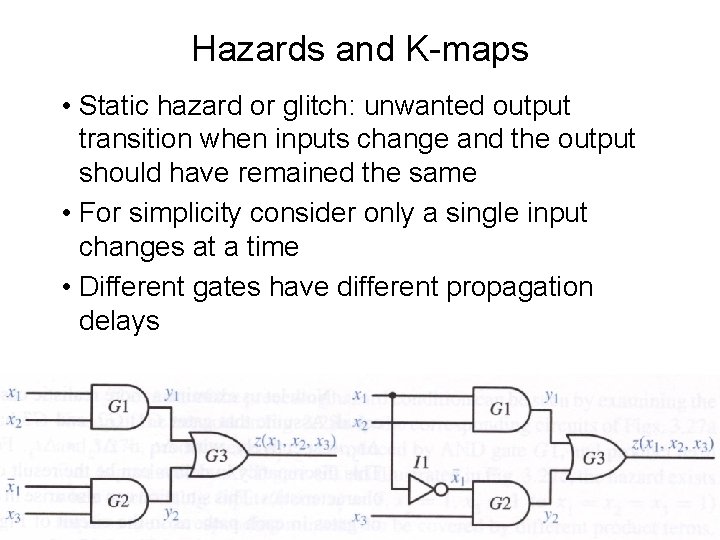
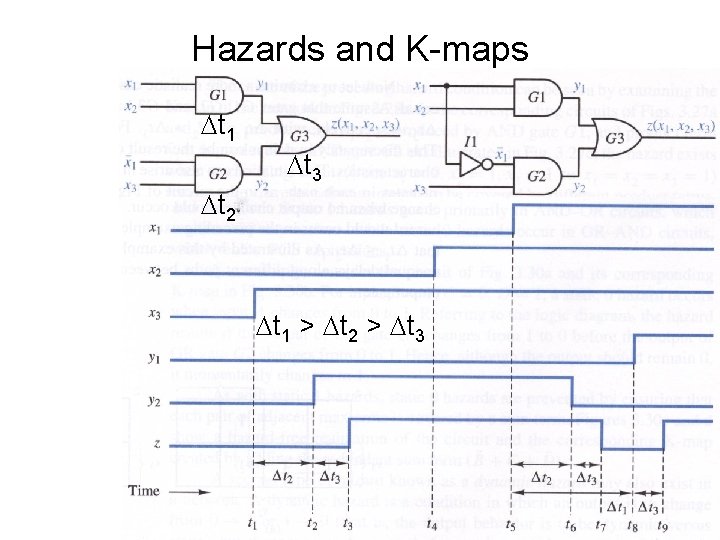
Hazards and K-maps • Static hazard or glitch: unwanted output transition when inputs change and the output should have remained the same • For simplicity consider only a single input changes at a time • Different gates have different propagation delays

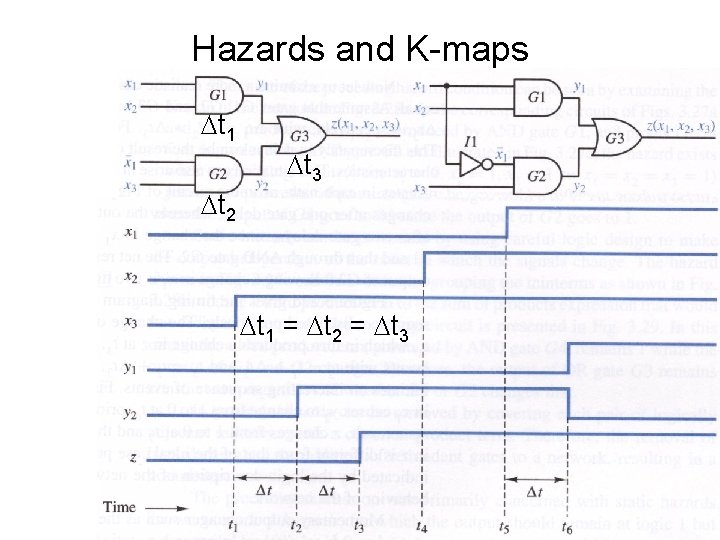
Hazards and K-maps t 1 t 3 t 2 t 1 = t 2 = t 3

Hazards and K-maps t 1 t 3 t 2 t 1 > t 2 > t 3

Hazards and K-maps • A hazard exists when a changing input requires corresponding minterms/maxterms to be covered by different product/sum terms • Remove hazards by bridging the gaps on the K -map:

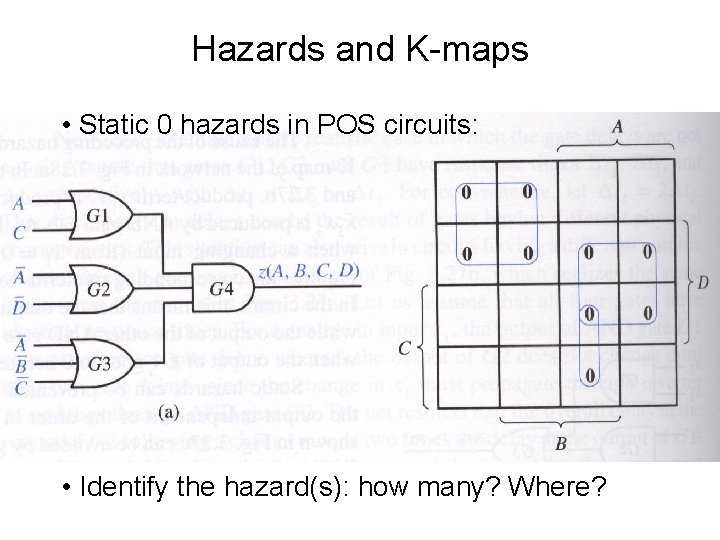
Hazards and K-maps • Hazard-free circuit: • Cover each pair of adjacent minterms by a different product term • Deliberate redundancy like this makes circuits impossible to test completely • Static 1 hazards: in SOP circuits: 1 0 1 • Static 0 hazards: in POS circuits: 0 1 0

Hazards and K-maps • Static 0 hazards in POS circuits: • Identify the hazard(s): how many? Where?

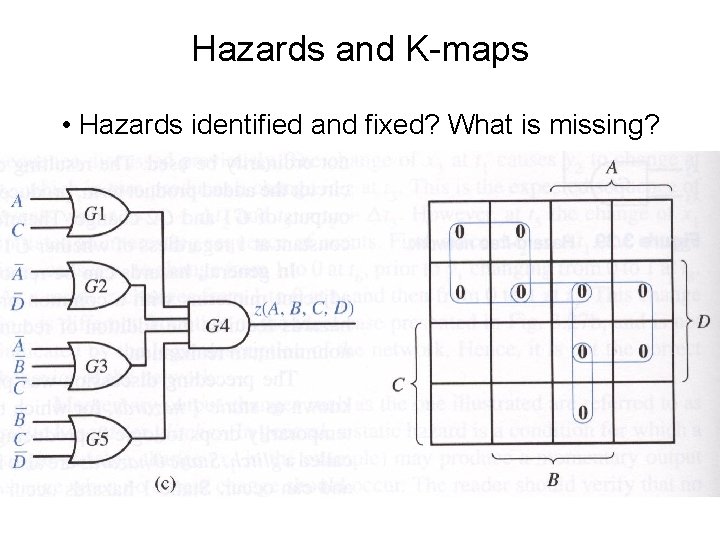
Hazards and K-maps • Hazards identified and fixed? What is missing?

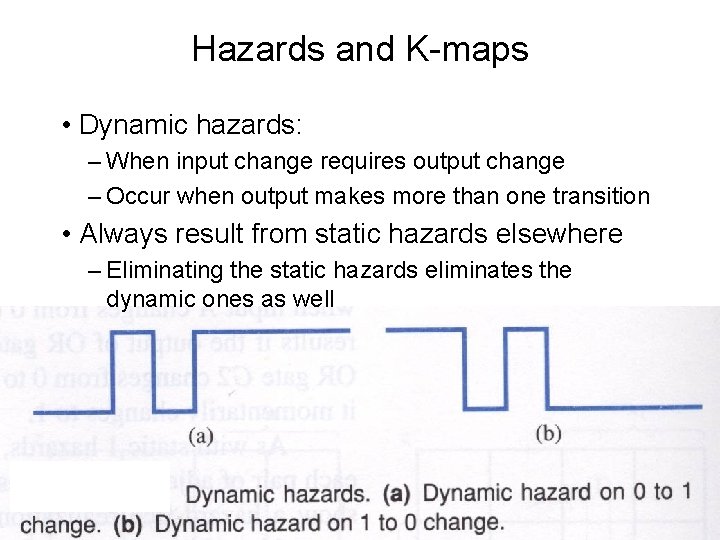
Hazards and K-maps • Dynamic hazards: – When input change requires output change – Occur when output makes more than one transition • Always result from static hazards elsewhere – Eliminating the static hazards eliminates the dynamic ones as well

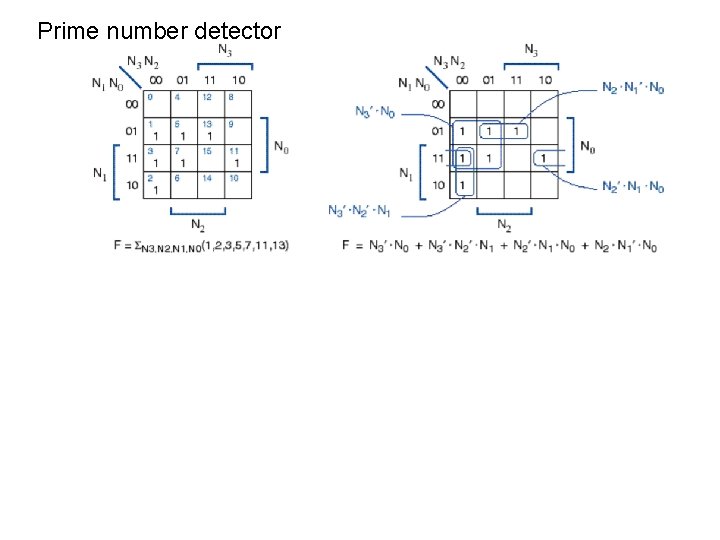
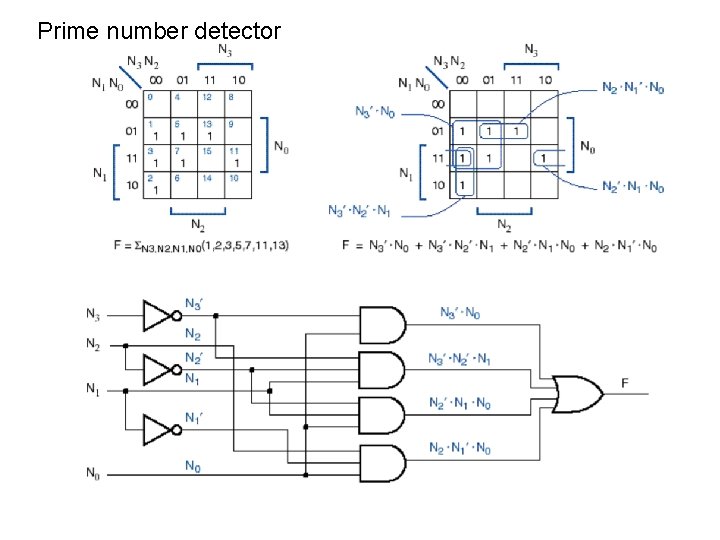
Prime number detector: F = (1, 2, 3, 5, 7, 11, 13) 00 N 3 N 2 01 11 10 00 01 x x x N 1 N 0 11 x 10 x x x 0001 0011 00 -1 0101 0111 01 -1 0 --1

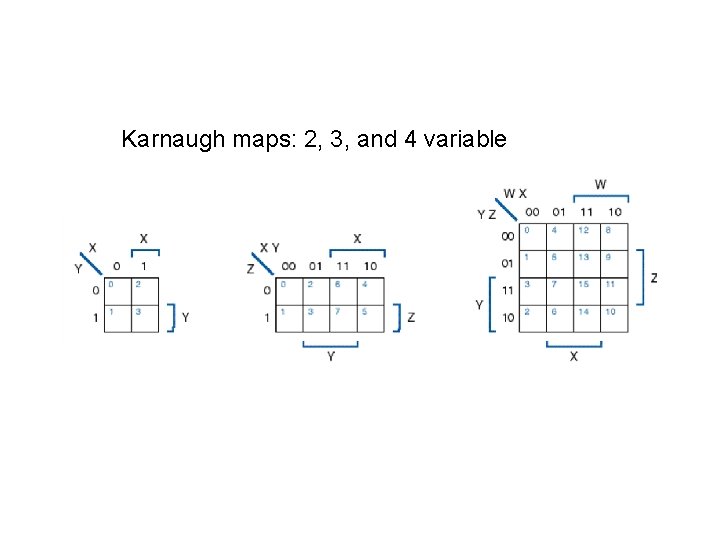
Karnaugh maps: 2, 3, and 4 variable

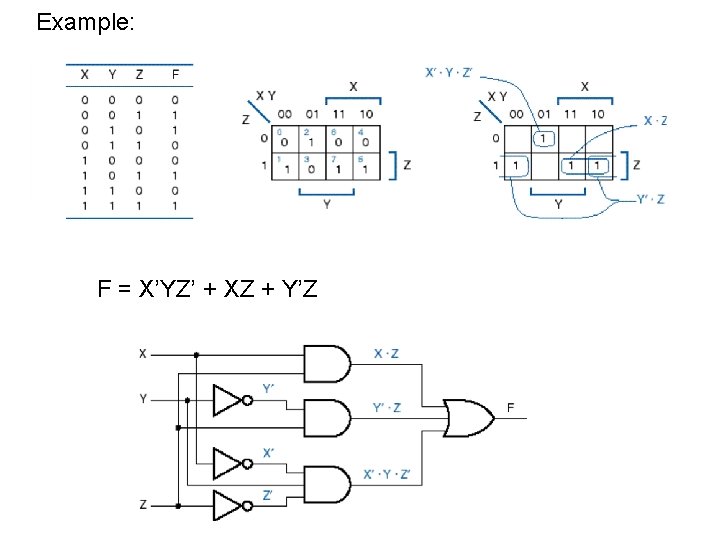
Example: F = X’YZ’ + XZ + Y’Z

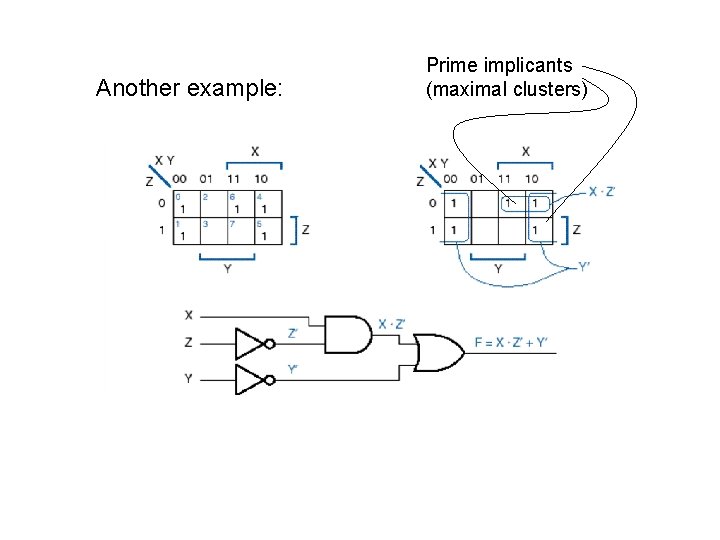
Another example: Prime implicants (maximal clusters)

Prime number detector

Prime number detector

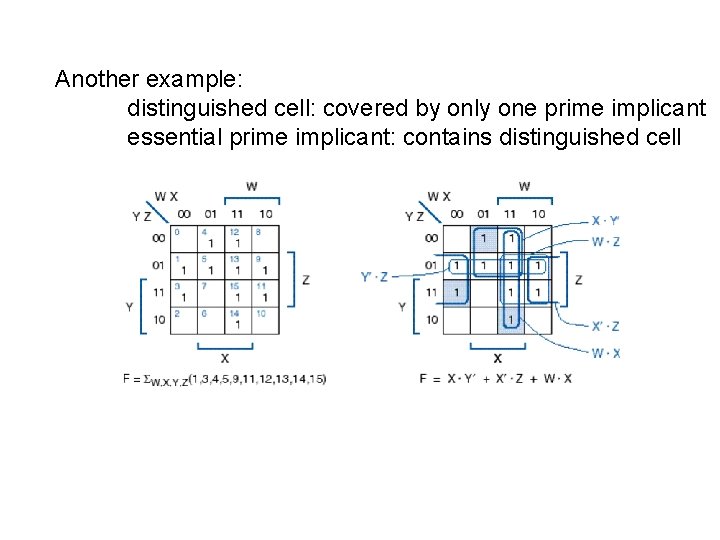
Another example: distinguished cell: covered by only one prime implicant essential prime implicant: contains distinguished cell

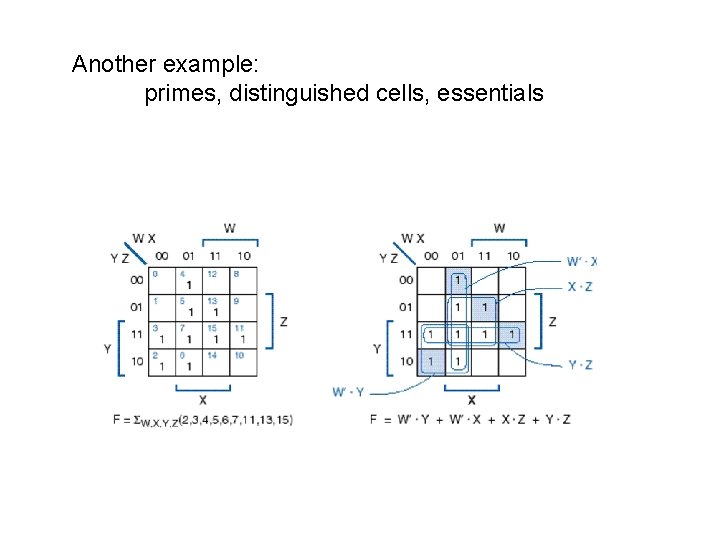
Another example: primes, distinguished cells, essentials

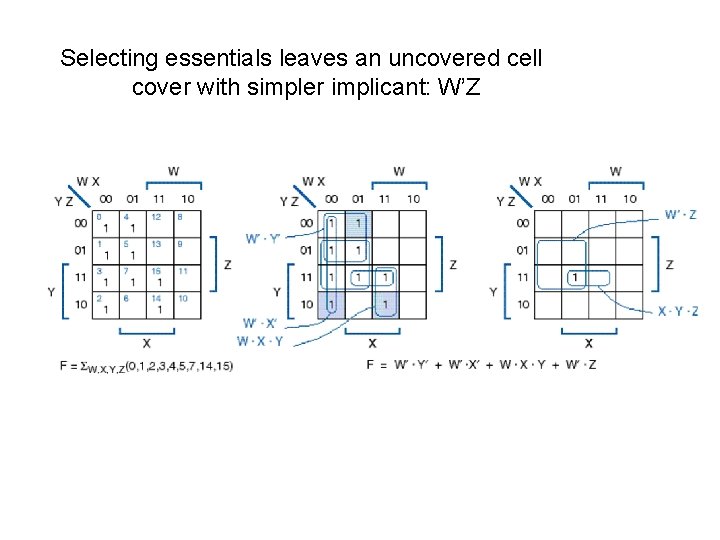
Selecting essentials leaves an uncovered cell cover with simpler implicant: W’Z

Eclipsing (in reduced map) P eclipses Q if P covers all of Q’s ones if P is no more expensive (same or fewer literals), then choose P over Q

Alas, no essential prime implicants branching: choose a cell and examine all implicants that cover that cell

Don’t cares. .

Multiple functions can use separate Karnaugh maps

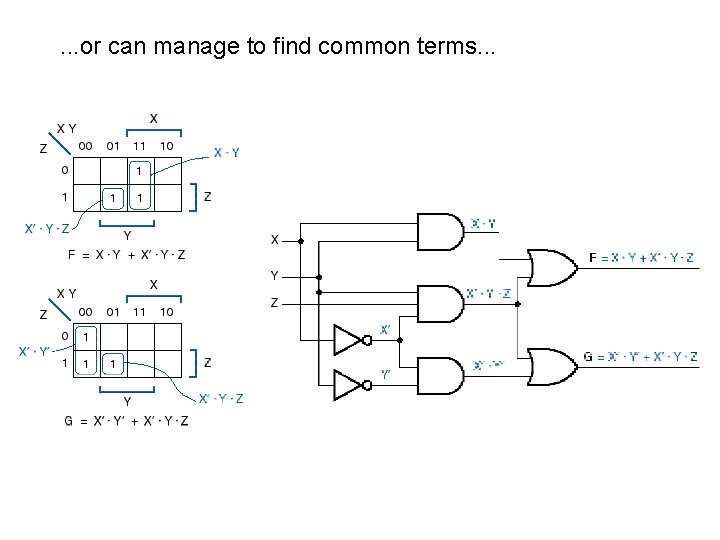
. . . or can manage to find common terms. . .

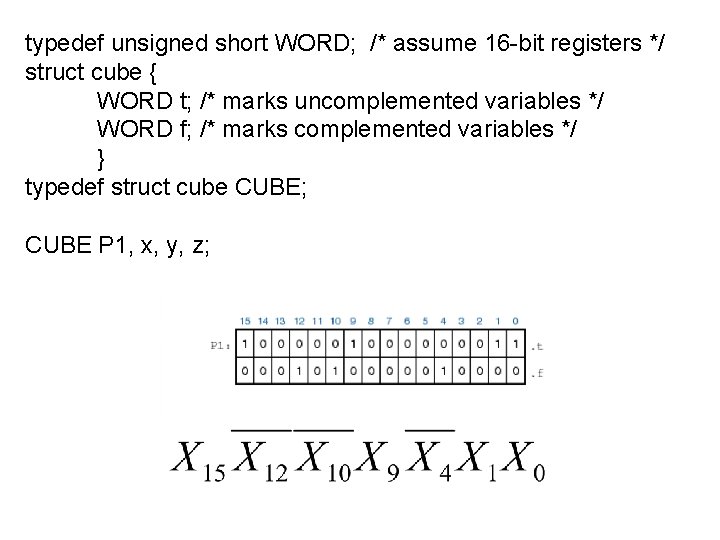
For more than 6 input variables, Karnaugh maps are difficult to manipulate Need computer program. . Quine-Mc. Cluskey algorithm

typedef unsigned short WORD; /* assume 16 -bit registers */ struct cube { WORD t; /* marks uncomplemented variables */ WORD f; /* marks complemented variables */ } typedef struct cube CUBE; CUBE P 1, x, y, z;

Example in four variables Equation: w x’ y z’ + w’ x’ y z’ = x’ y z’ Karnaugh map: wx 00 01 yz 00 01 11 10 1 Cubes (last four bits): 1010 0010 = 1000 ==> single one in common position ==> combinable 0101 1101 = 1000 1010 & 0010 ==> w now missing, new cube corresponds to z’ y z’ 0101 & 1101 = 0101


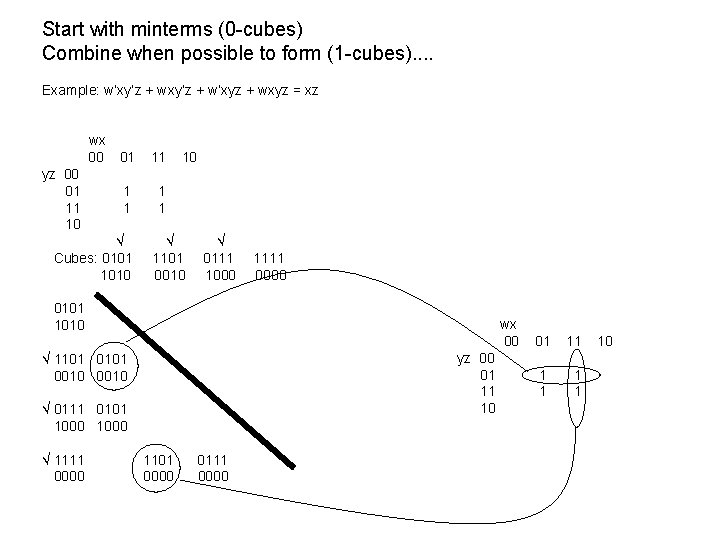
Start with minterms (0 -cubes) Combine when possible to form (1 -cubes). . Example: w’xy’z + w’xyz + wxyz = xz yz 00 01 11 10 wx 00 01 11 1 1 Cubes: 0101 1010 1101 0010 0111 1000 1111 0000 10 1101 0010 0101 1101 = 1000 1010 0010 = 1000 0111 1000 1111 0000 0101 & 1101 = 0101 1010 & 0010 = 0010

Start with minterms (0 -cubes) Combine when possible to form (1 -cubes). . Example: w’xy’z + w’xyz + wxyz = xz yz 00 01 11 10 wx 00 01 11 1 1 Cubes: 0101 1010 10 1101 0010 0101 1101 = 1000 1010 0010 = 1000 0111 1000 0101 & 1101 = 0101 1010 & 0010 = 0010 1111 0000 0101 1010 1101 0010 0111 1000 1111 0000 wx 00 yz 00 01 11 1 1 10

Start with minterms (0 -cubes) Combine when possible to form (1 -cubes). . Example: w’xy’z + w’xyz + wxyz = xz yz 00 01 11 10 wx 00 01 11 1 1 Cubes: 0101 1010 10 1101 0010 0111 1000 1111 0000 0101 1010 wx 00 1101 0010 yz 00 01 11 10 0111 0101 1000 1111 0000 1101 0000 0111 0000 01 11 1 1 10

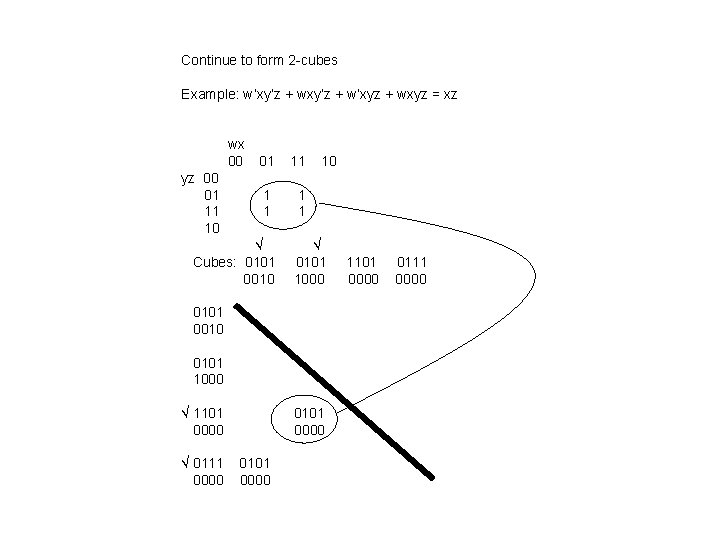
Continue to form 2 -cubes Example: w’xy’z + w’xyz + wxyz = xz yz 00 01 11 10 wx 00 01 11 1 1 Cubes: 0101 0010 10 0101 1000 0101 0010 0101 1000 1101 0000 0111 0000 0101 0000 1101 0000 0111 0000

Quine-Mc. Cluskey Algorithm: Read in all minterms (0 -cubes); mark all 0 -cubes “uncovered”; for (m = 0; m < Nvar; m++) for (j = 0; j < Ncubes[m]; j++) for (k = j + 1; k < Ncubes[m]; k++) if (combinable(cube[m][j], cube[m][k])) { mark cube[m][j] and cube[m][k] “covered” temp = combined cube; if (temp not already at level m + 1) { add temp to level m + 1; mark temp “uncovered” } }

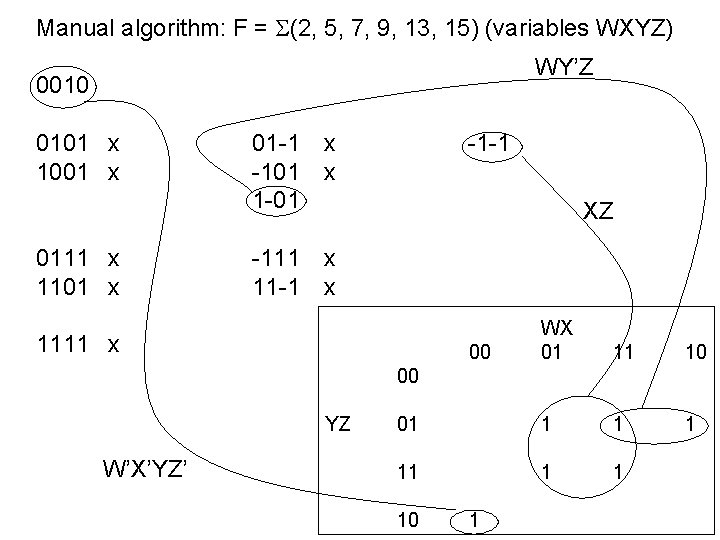
Manual algorithm: F = (2, 5, 7, 9, 13, 15) (variables WXYZ) uncovered terms 0010 0101 1001 01 -1 -101 1 -01 0111 1101 -111 11 -1 1111 -1 -1

Manual algorithm: F = (2, 5, 7, 9, 13, 15) (variables WXYZ) WY’Z 0010 0101 x 1001 x 0111 x 1101 x 01 -1 x -101 x 1 -01 -1 -1 XZ -111 x 11 -1 x WX 01 11 10 01 1 1111 x 00 00 YZ W’X’YZ’ 10 1

Prime Implicants 0010 1 -01 -1 -1 Minterms 2 5 7 9 13 15 x x x x distinguished minterms (cells): 2, 5, 7, 9, 15 essential prime implicants: 0010, 1 -01, -1 -1 (all) F = 0010 + 1 -01 + -1 -1 = W’X’YZ’ + WY’Z + XZ

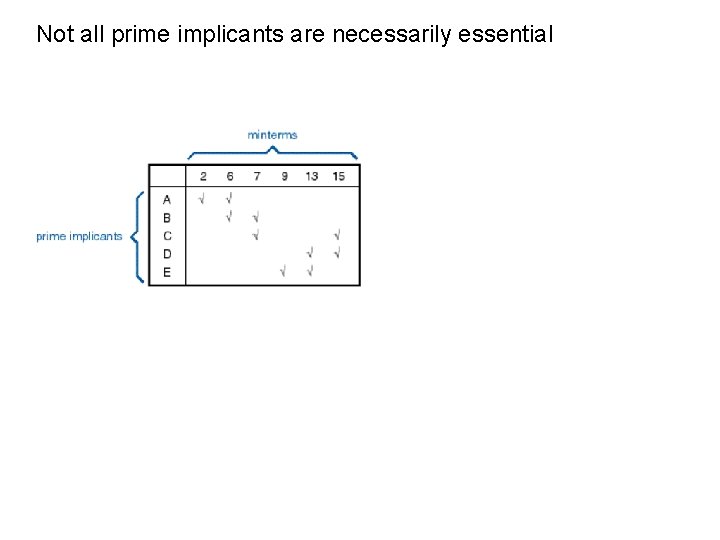
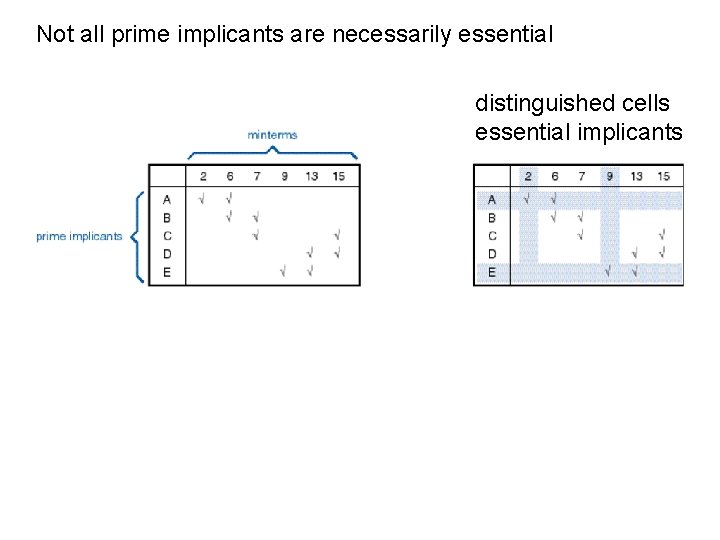
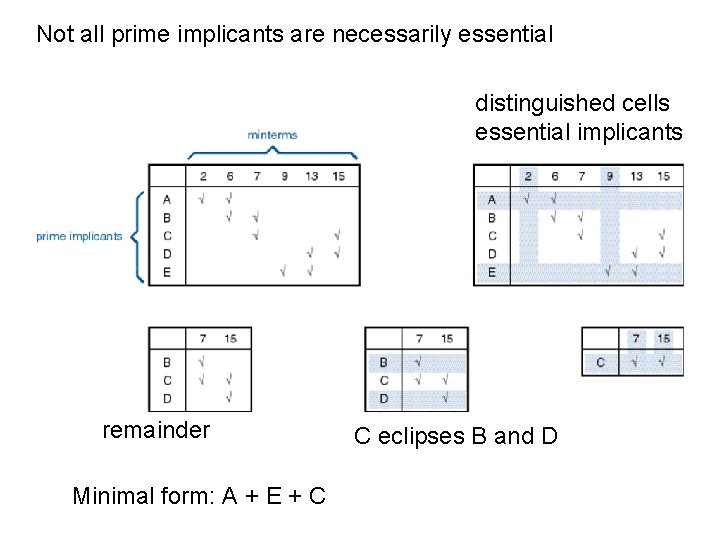
Not all prime implicants are necessarily essential distinguished cells essential implicants remainder Minimal form: A + E + C C eclipses B and D

Not all prime implicants are necessarily essential distinguished cells essential implicants remainder Minimal form: A + E + C C eclipses B and D

Not all prime implicants are necessarily essential distinguished cells essential implicants remainder Minimal form: A + E + C C eclipses B and D

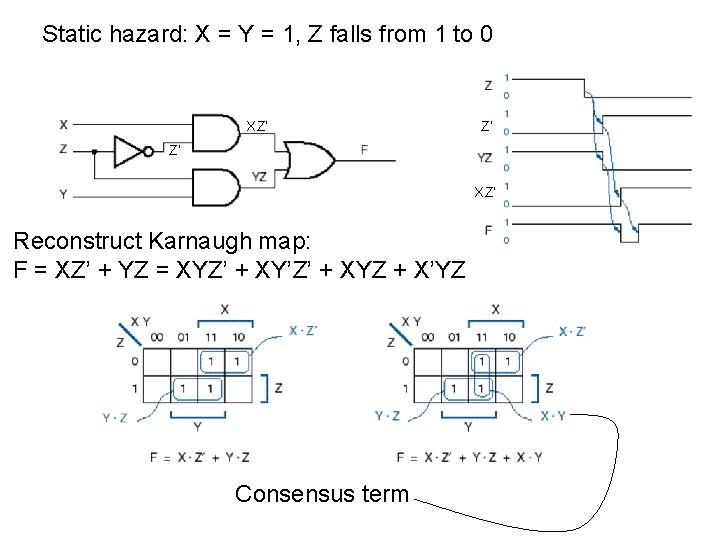
Static hazard: X = Y = 1, Z falls from 1 to 0 XZ’ Z’ Z’ XZ’ Reconstruct Karnaugh map: F = XZ’ + YZ = XYZ’ + XY’Z’ + XYZ + X’YZ Consensus term

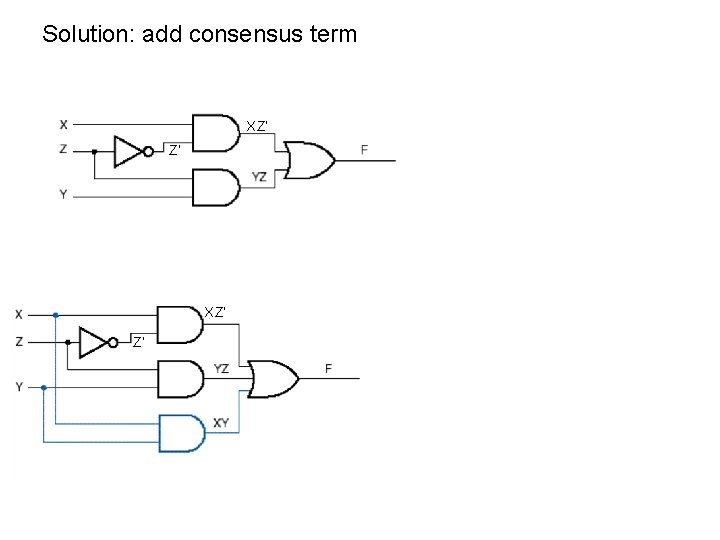
Solution: add consensus term XZ’ Z’ Z’ XZ’ Z’ Consensus term
 Phylum chordata
Phylum chordata The scale structure covering the exterior of the hair
The scale structure covering the exterior of the hair Coverings of the brain
Coverings of the brain Cigna not covering vitamin d testing
Cigna not covering vitamin d testing Rigid outer covering of plant cells
Rigid outer covering of plant cells Double layered membrane covering the lungs
Double layered membrane covering the lungs To safely transport cargo use
To safely transport cargo use Sequential covering algorithm example
Sequential covering algorithm example Fibroareolar sheath
Fibroareolar sheath Covering letter for resignation
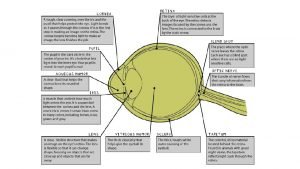
Covering letter for resignation Thick, clear jelly that helps give the eyeball its shape.
Thick, clear jelly that helps give the eyeball its shape. Cigna not covering vitamin d testing
Cigna not covering vitamin d testing Floor covering weekly top 50
Floor covering weekly top 50 Erroneous cubic cell
Erroneous cubic cell Chordate animals
Chordate animals Vaginal hydrocele
Vaginal hydrocele Spinous pattern
Spinous pattern Find duck
Find duck Oolab shoes
Oolab shoes Set covering machine
Set covering machine A cellular column running through the center of the hair
A cellular column running through the center of the hair Nun head covering
Nun head covering Whats a covering letter
Whats a covering letter Covering tracks
Covering tracks Placing an order email sample
Placing an order email sample Spermatic cord coverings
Spermatic cord coverings Tough outer covering of bone
Tough outer covering of bone Sole horn nail
Sole horn nail Signed statement for head covering
Signed statement for head covering Pericardial fluid
Pericardial fluid Body covering of animals
Body covering of animals Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Dot
Dot điện thế nghỉ
điện thế nghỉ Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ độ dài liên kết
độ dài liên kết Gấu đi như thế nào
Gấu đi như thế nào Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Một số thể thơ truyền thống
Một số thể thơ truyền thống Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Ng-html
Ng-html Hệ hô hấp
Hệ hô hấp Thế nào là số nguyên tố
Thế nào là số nguyên tố đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Glasgow thang điểm
Glasgow thang điểm ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Tư thế ngồi viết
Tư thế ngồi viết Cái miệng nó xinh thế
Cái miệng nó xinh thế Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Bổ thể
Bổ thể Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu