Chapter 5 Probability What Are the Chances Section

Chapter 5 Probability: What Are the Chances? Section 5. 2 Probability Rules

Probability Rules LEARNING TARGETS By the end of this section, you should be able to: üGIVE a probability model for a chance process with equally likely outcomes and USE it to find the probability of an event. üUSE basic probability rules, including the complement rule and the addition rule for mutually exclusive events. üUSE a two-way table or Venn diagram to model a chance process and calculate probabilities involving two events. üAPPLY the general addition rule to calculate probabilities. Starnes/Tabor, The Practice of Statistics

Probability Models rt Steve Go on/Getty Images In Section 5. 1, we used simulation to imitate chance behavior. Fortunately, we don’t have to always rely on simulations to determine the probability of a particular outcome. A probability model is a description of some chance process that consists of two parts: a list of all possible outcomes and the probability for each outcome. The list of all possible outcomes is called the sample space. A sample space can be very simple or very complex. Starnes/Tabor, The Practice of Statistics

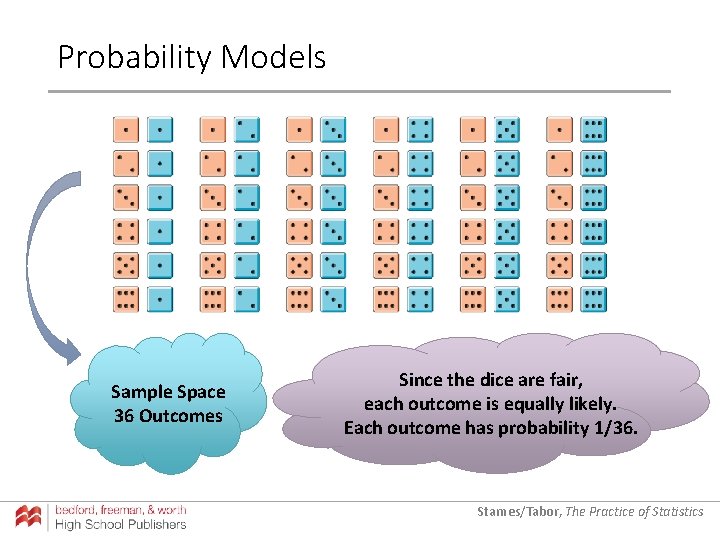
Probability Models Sample Space 36 Outcomes Since the dice are fair, each outcome is equally likely. Each outcome has probability 1/36. Starnes/Tabor, The Practice of Statistics

Probability Models An event is any collection of outcomes from some chance process. Let A = getting a sum of 5 when two fair dice are rolled rt Steve Go on/Getty Images There are 4 outcomes that result in a sum of 5. Starnes/Tabor, The Practice of Statistics

Probability Models Finding Probabilities: Equally Likely Outcomes rt Steve Go on/Getty Images Starnes/Tabor, The Practice of Statistics

Basic Probability Rules The complement rule says that P (AC) = 1 – P(A), where AC is the complement of event A; that is, the event that A does not occur. Starnes/Tabor, The Practice of Statistics

Basic Probability Rules The complement rule says that P (AC) = 1 – P(A), where AC is the complement of event A; that is, the event that A does not occur. Starnes/Tabor, The Practice of Statistics

Basic Probability Rules If we roll two fair dice, what is the probability that the sum is 6? If we roll two fair dice, what is the probability that the sum is 5 or 6? Two events A and B are mutually exclusive if they have no outcomes in common and so can never occur together—that is, if P(A and B) = 0. The addition rule for mutually exclusive events A and B says that P(A or B) 5= P(A) + P(B) Starnes/Tabor, The Practice of Statistics

Basic Probability Rules If we roll two fair dice, what is the probability that the sum is 6? If we roll two fair dice, what is the probability that the sum is 5 or 6? ts. n e ev e v lusi c x y e l l a tu u : r m o N Two events A and B are mutually exclusive if they have no f O y I l n T s o k outcomes in common and so can never occur together—that is, if r CAU wo e l P(A and B) = 0. is ru thrule for mutually exclusive events A and B says that t a The addition e th t o N P(A or B) 5= P(A) + P(B) Starnes/Tabor, The Practice of Statistics

Basic Probability Rules We can summarize the basic probability rules in symbolic form. Basic Probability Rules Starnes/Tabor, The Practice of Statistics

Basic Probability Rules Problem: Suppose you tear open the corner of a bag of M&M’S® Milk Chocolate Niels Poulsen std/Alamy Candies, pour one candy into your hand, and observe the color. According to Mars, Inc. , the maker of M&M’S, the probability model for a bag from its Cleveland factory is: (a) Explain why this is a valid probability model. (a) The probability of each outcome is a number between 0 and 1. The sum of the probabilities is 0. 207 + 0. 205 + 0. 198 + 0. 135 + 0. 131 + 0. 124 = 1. Starnes/Tabor, The Practice of Statistics

Basic Probability Rules Problem: Suppose you tear open the corner of a bag of M&M’S® Milk Chocolate Niels Poulsen std/Alamy Candies, pour one candy into your hand, and observe the color. According to Mars, Inc. , the maker of M&M’S, the probability model for a bag from its Cleveland factory is: (a) Explain why this is a valid probability model. (b) Find the probability that you don’t get a blue M&M. (b) P (not blue) = 1 – P(blue) = 1 – 0. 207 = 0. 793 Starnes/Tabor, The Practice of Statistics

Basic Probability Rules Problem: Suppose you tear open the corner of a bag of M&M’S® Milk Chocolate Niels Poulsen std/Alamy Candies, pour one candy into your hand, and observe the color. According to Mars, Inc. , the maker of M&M’S, the probability model for a bag from its Cleveland factory is: (a) Explain why this is a valid probability model. (b) Find the probability that you don’t get a blue M&M. (c) What’s the probability that you get an orange or a brown M&M? (c) P (orange or brown) = P (orange) + P (brown) = 0. 205 + 0. 124 = 0. 329 Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule There are two different uses of the word or in everyday life. When you are asked if you want “soup or salad, ” the waiter wants you to choose one or the other, but not both. However, when you order coffee and are asked if you want “cream or sugar, ” it’s OK to ask for one or the other or both. In mathematics and probability, “A or B” means one or the other or both. When you’re trying to find probabilities involving two events, like P(A or B), a two-way table can display the sample space in a way that makes probability calculations easier. Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule Big Cheese Photo/Super stock Problem: Students in a college statistics class wanted to find out how common it is for young adults to have their ears pierced. They recorded data on two variables— gender and whether or not the student had a pierced ear—for all 178 people in the class. The two-way table summarizes the data. Suppose we choose a student from the class at random. Define event A as getting a male student and event B as getting a student with a pierced ear. (a) Find P(B). Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule Photo/Super Big Cheese stock Problem: Students in a college statistics class wanted to find out how common it is for young adults to have their ears pierced. They recorded data on two variables— gender and whether or not the student had a pierced ear—for all 178 people in the class. The two-way table summarizes the data. Suppose we choose a student from the class at random. Define event A as getting a male student and event B as getting a student with a pierced ear. (a) Find P(B). (b) Find P(A and B). Interpret this value in context. Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule Photo/Super Big Cheese (b) There’s about an 11% chance that a randomly selected student from this class is male and has a pierced ear. stock Problem: Students in a college statistics class wanted to find out how common it is for young adults to have their ears pierced. They recorded data on two variables— gender and whether or not the student had a pierced ear—for all 178 people in the class. The two-way table summarizes the data. Suppose we choose a student from the class at random. Define event A as getting a male student and event B as getting a student with a pierced ear. (a) Find P(B). (b) Find P(A and B). Interpret this value in context. Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule Photo/Super Big Cheese stock Problem: Students in a college statistics class wanted to find out how common it is for young adults to have their ears pierced. They recorded data on two variables— gender and whether or not the student had a pierced ear—for all 178 people in the class. The two-way table summarizes the data. Suppose we choose a student from the class at random. Define event A as getting a male student and event B as getting a student with a pierced ear. (a) Find P(B). (b) Find P(A and B). Interpret this value in context. (c) Find P(A or B). Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule Part (c) of the example reveals an important fact about finding the probability P(A or B): we can’t use the addition rule for mutually exclusive events unless events A and B have no outcomes in common. Starnes/Tabor, The Practice of Statistics

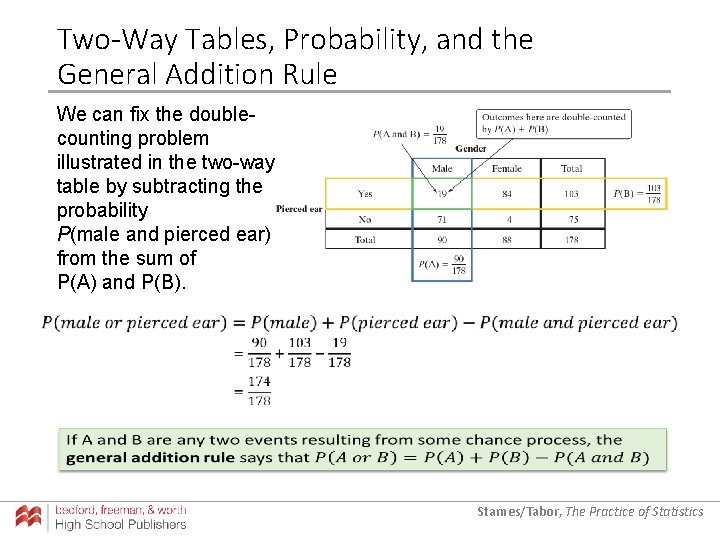
Two-Way Tables, Probability, and the General Addition Rule We can fix the doublecounting problem illustrated in the two-way table by subtracting the probability P(male and pierced ear) from the sum of P(A) and P(B). Starnes/Tabor, The Practice of Statistics

Two-Way Tables, Probability, and the General Addition Rule Problem: A survey of all residents in a large apartment complex reveals that 68% use Facebook, 28% use Instagram, and 25% do both. Suppose we select a resident at random. What’s the probability that the person uses Facebook or uses Instagram? Let event F = uses Facebook and = uses Instagram. P(F or I) = P(F) + P(I) – P(F and I) = 0. 68 + 0. 28 – 0. 25 = 0. 71 Ann Heath I Starnes/Tabor, The Practice of Statistics

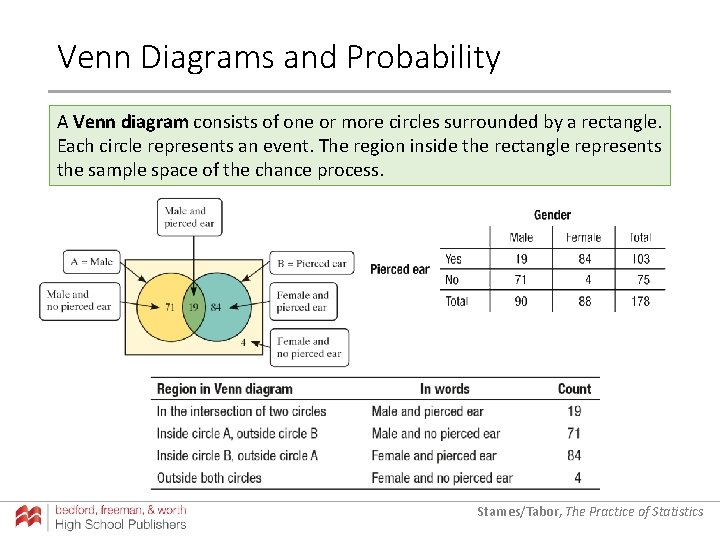
Venn Diagrams and Probability A Venn diagram consists of one or more circles surrounded by a rectangle. Each circle represents an event. The region inside the rectangle represents the sample space of the chance process. Starnes/Tabor, The Practice of Statistics

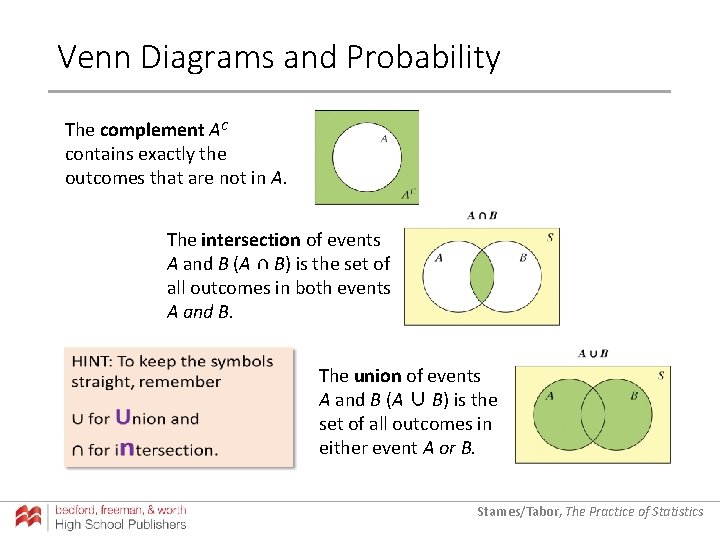
Venn Diagrams and Probability The complement AC contains exactly the outcomes that are not in A. The intersection of events A and B (A ∩ B) is the set of all outcomes in both events A and B. The union of events A and B (A ∪ B) is the set of all outcomes in either event A or B. Starnes/Tabor, The Practice of Statistics

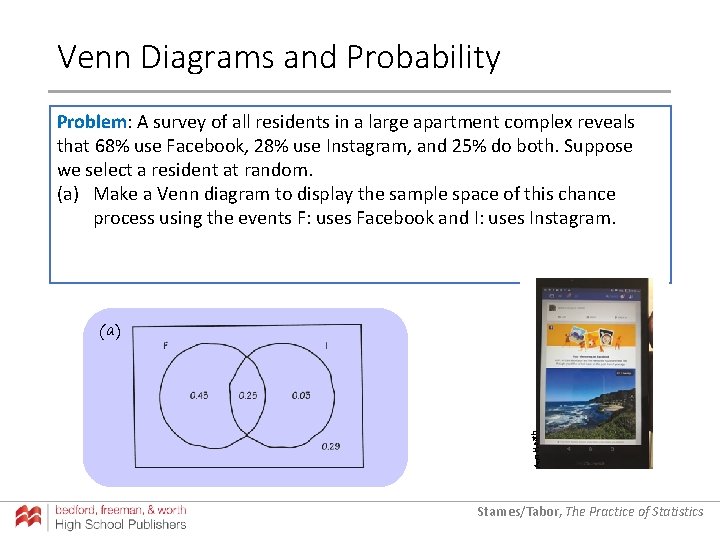
Venn Diagrams and Probability Problem: A survey of all residents in a large apartment complex reveals that 68% use Facebook, 28% use Instagram, and 25% do both. Suppose we select a resident at random. (a) Make a Venn diagram to display the sample space of this chance process using the events F: uses Facebook and I: uses Instagram. Ann Heath (a) Starnes/Tabor, The Practice of Statistics

Venn Diagrams and Probability (b) P(no Facebook and no Instagram) = 0. 29 Ann Heath Problem: A survey of all residents in a large apartment complex reveals that 68% use Facebook, 28% use Instagram, and 25% do both. Suppose we select a resident at random. (a) Make a Venn diagram to display the sample space of this chance process using the events F: uses Facebook and I: uses Instagram. (b) Find the probability that the person uses neither Facebook nor Instagram. Starnes/Tabor, The Practice of Statistics