Binomial Probability Probability Simple Theoretical Probability Experimental Probability

Binomial Probability

Probability • • • Simple Theoretical Probability Experimental Probability Independent Probability Dependent Probability Conditional Probability

Binomial Probability • Two mutually exclusive outcomes sucesses (p) failures (1 -p) • Sometimes called a Bernoulli trial • Trials must be independent

Binomial Probability • Must calculate and multiply 3 separate factors • • • The number of ways to select success The probability of failure

Formula There are several different notations for Binomial Probability. Each one will give the correct answer. It depends upon which source you use as to which notation is used.

Formula Notation #1 • The probability of achieving exactly k successes in n trials is shown as P(k successes in n trials)= n = number of trials k = number of successes n – k = number of failures p = probability of success in one trial q = 1 – p = probability of failure in one trial

Formula Notation #2 • The probability of an event, p, occurring exactly r times: n = number of trials r = number of specific events you wish to obtain p = probability that the event will occur q = probability that the event will not occur (q = 1 - p, the complement of the event)

Example If you flip a coin 11 times, what is the probability of getting exactly 2 heads. 3 factors to calculate = ways to choose success Sucess = heads (2) and Probability of heads = ½ Failure = tails (9) and Probability of tails= ½

• Calculate Notice that the exponents add to 11. Notice that out of 11 trials we are looking for 2 successes- therefore 9 failures.

Binomial Example 2 • A large lot of manufactured items contains 10% defectives. In a random sample of 6 items, what is the probability that exactly 2 are defective? • What are the 3 factors to calculate? Number of ways for defective = success- 2 and probability of success=. 1 Failure- 4 and probability of failure =. 9

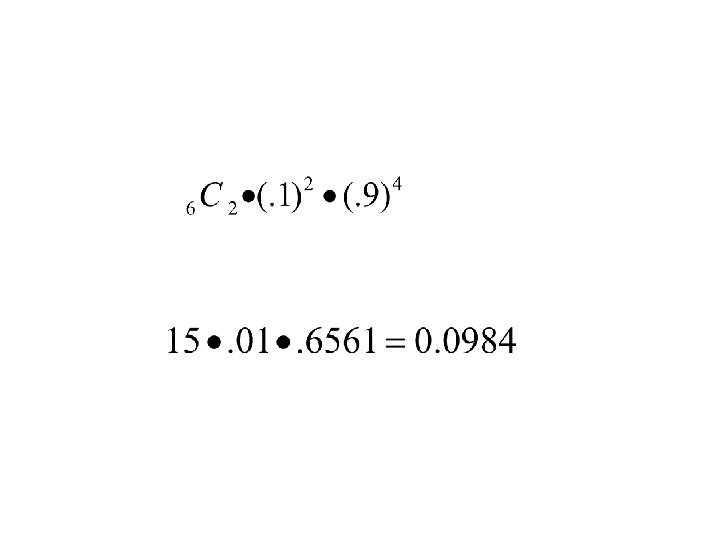
Binomial Example 3 Sixty percent of the workers in a plant belong to a union. A random sample of 12 is chosen. Find the probability that exactly 4 belong to a union. Name the 3 factors to calculate Ways to choose success (belonging to the union) How many successes? Probability of success? How many failures? Probability of failure?

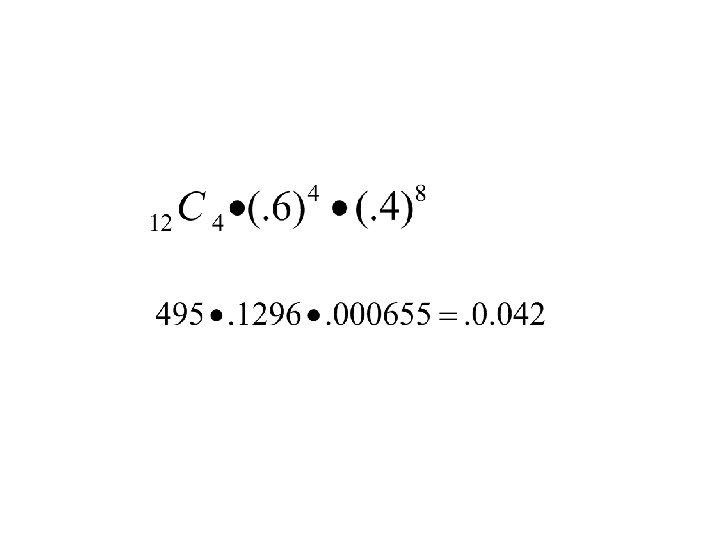
Helpful Information Decimals are easier than fractions with these large calculations Pascal’s Triangle may be used in place of the combination formula Make sure that you are defining your successes and failures by the information in the problem- not by your own definition of success and failure

More to Come We will be working on binomial distributions next week when we learn about making dotplots and discussing sample distribution.