Chapter 8 Quadratic Functions Copyright 2015 2011 2007

Chapter 8 Quadratic Functions Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -

Chapter Sections 8. 1 – Solving Quadratic Equations by Completing the Square 8. 2 – Solving Quadratic Equations by the Quadratic Formulas 8. 3 – Quadratic Equations: Applications and Problem Solving 8. 4 – Writing Equations in Quadratic Form 8. 5 – Graphing Quadratic Functions 8. 6 – Quadratic and Other Inequalities in One Variable Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -2 2

§ 8. 5 Graphing Quadratic Functions Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -

Quadratic Functions Quadratic Function A quadratic function is a function that can be written in the form f(x) = ax 2 + bx + c For real numbers a, b, and c, with a ≠ 0. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -4 4

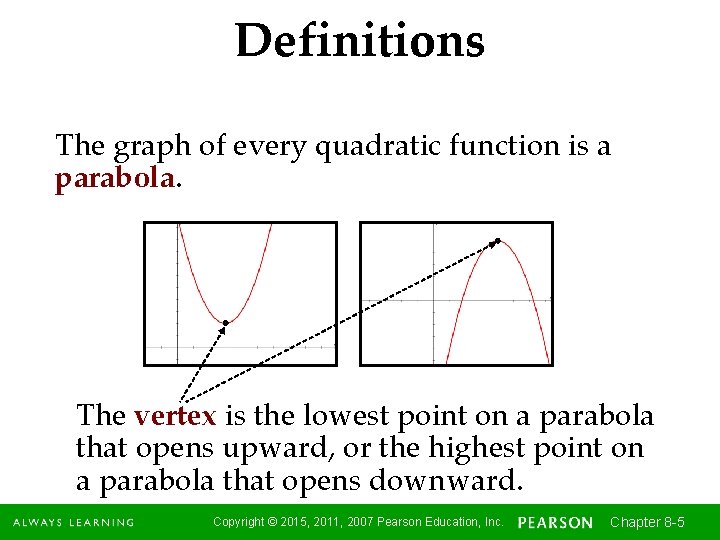
Definitions The graph of every quadratic function is a parabola. The vertex is the lowest point on a parabola that opens upward, or the highest point on a parabola that opens downward. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -5 5

Definitions Graphs of quadratic equations have symmetry about a line through the vertex. This line is called the axis of symmetry. The sign of a, the numerical coefficient of the squared term, determines whether the parabola will open upward or downward. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -6 6

Vertex of a Parabola The parabola represented by the function f(x) = ax 2 + bx + c will have vertex Since we often find the y-coordinate of the vertex by substituting the x-coordinate of the vertex into f(x), the vertex may also be designated as Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -7 7

Axis of Symmetry of a Parabola Axis of Symmetry For a quadratic function of the form f(x) = ax 2 + bx + c, the equation of the axis of symmetry of the parabola is Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -8 8

x-Intercepts of a Parabola To find the x-intercepts (if there any) of a quadratic function, solve the equation ax 2 + bx + c = 0 for x. This equation may be solved by factoring, by using the quadratic formula, or by completing the square. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -9 9

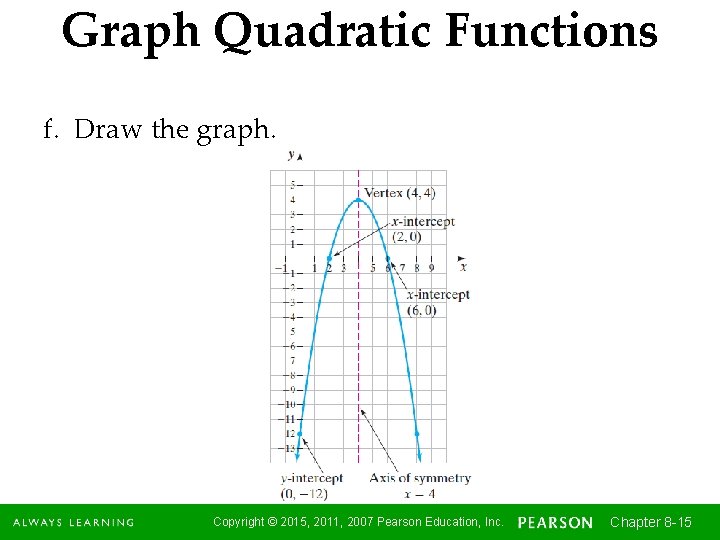
Graph Quadratic Functions Example Consider the quadratic function y = x 2 + 8 x – 12. a. Determine whether the parabola opens upward or downward. b. Find the y-intercept. c. Find the vertex. d. Find the equation of the axis of symmetry. e. Find the x-intercepts, if any. f. Draw the graph. continued Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -10 10

Graph Quadratic Functions a. Since a is -1, which is less than 0, the parabola opens downward. b. To find the y-intercept, set x = 0 and solve for y. The y-intercept is (0, 12) continued Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -11 11

Graph Quadratic Functions c. First, find the x-coordinate, then find the ycoordinate of the vertex. From the function, a = -1, b = 8, and c = -12. Since the x-coordinate of the vertex is not a fraction, we will substitute x = 4 into the original function to determine the y-coordinate of the vertex. The vertex is (4, 4). Copyright © 2015, 2011, 2007 Pearson Education, Inc. continued Chapter 8 -12 12

Graph Quadratic Functions d. Since the axis of symmetry is a vertical line through the vertex, the equation is found using the same formula used to find the x-coordinate of the vertex (see part c). Thus, the equation of the axis of symmetry is x = 4. continued Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -13 13

Graph Quadratic Functions e. To find the x-intercepts, set y = 0. Thus, the x-intercepts are (2, 0) and (6, 0). These values could also be found by the quadratic formula (or by completing the square). continued Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -14 14

Graph Quadratic Functions f. Draw the graph. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -15 15

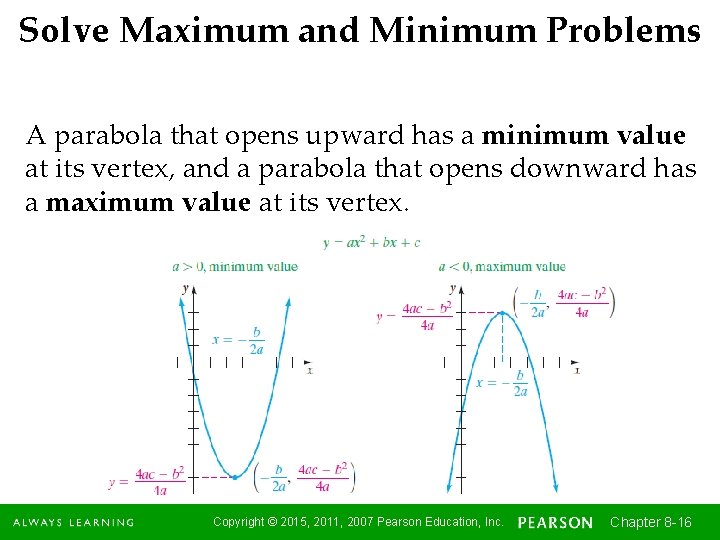
Solve Maximum and Minimum Problems A parabola that opens upward has a minimum value at its vertex, and a parabola that opens downward has a maximum value at its vertex. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -16 16

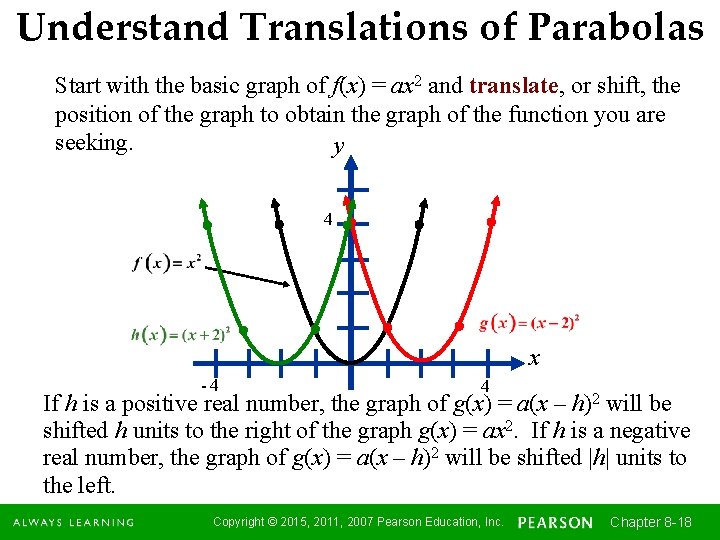
Understand Translations of Parabolas Start with the basic graph of f(x) = ax 2 and translate, or shift, the position of the graph to obtain the graph of the function you are y seeking. 4 x -4 4 Notice that the value of a in the graph f(x) = ax 2 determines the width of the parabola. As |a| gets larger, the parabola gets narrower, and as |a| gets smaller, the parabola gets wider. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -17 17

Understand Translations of Parabolas Start with the basic graph of f(x) = ax 2 and translate, or shift, the position of the graph to obtain the graph of the function you are seeking. y 4 x -4 4 If h is a positive real number, the graph of g(x) = a(x – h)2 will be shifted h units to the right of the graph g(x) = ax 2. If h is a negative real number, the graph of g(x) = a(x – h)2 will be shifted |h| units to the left. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -18 18

Understand Translations of Parabolas Start with the basic graph of f(x) = ax 2 and translate, or shift, the position of the graph to obtain the graph of the function you are y seeking. 4 x -4 4 In general, the graph of g(x) = ax 2 + k is the graph of f(x) = ax 2 shifted k units up if k is a positive real number and |k| units down if k is a negative real number. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -19 19

Understand Translations of Parabolas Parabola Shifts For any function f(x) = ax 2, the graph of g(x) = a(x-h)2 + k will have the same shape as the graph of f(x). The graph of g(x) will be the graph of f(x) shifted as follows: • If h is a positive real number, the graph will be shifted h units to the right. • If h is a negative real number, the graph will be shifted |h| units to the left. • If k is a positive real number, the graph will be shifted k units up. • If k is a negative real number, the graph will be shifted |k| units down. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -20 20

Understand Translations of Parabolas Axis of Symmetry and Vertex of a Parabola The graph of any function of the form f(x) = a(x – h)2 + k will be a parabola with axis of symmetry x = h and vertex at (h, k). Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -21 21

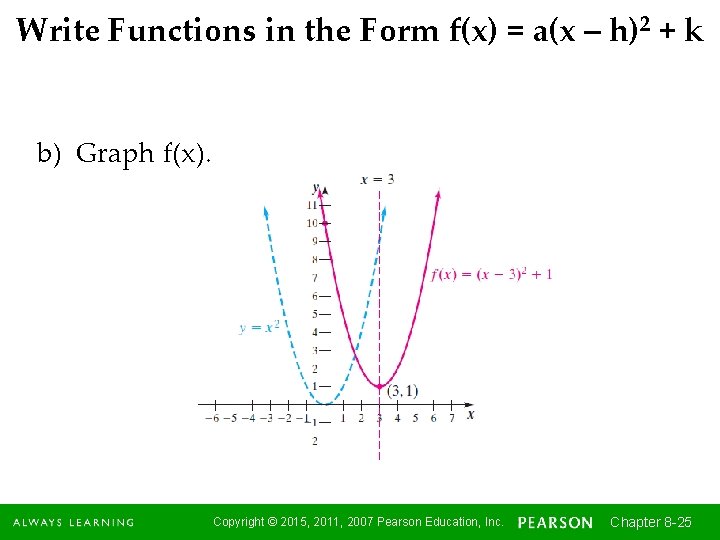
Write Functions in the Form f(x) = a(x – h)2 + k If we wish to graph parabolas using translations, we need to change the form of a function from f(x) = ax 2 + bx + c to f(x) = a(x – h)2 + k. To do this we complete the square as we discussed in Section 8. 1. Example Given f(x) = x 2 – 6 x + 10, a) Write f(x) in the form of f(x) = a(x – h)2 + k. b) Graph f(x). Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -22 22

Write Functions in the Form f(x) = a(x – h)2 + k a) We use the x 2 and -6 x terms to obtain a perfect square trinomial. Now we take half the coefficient of the x-term and square it. We then add this value, 9, within the parentheses. continued Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -23 23

Write Functions in the Form f(x) = a(x – h)2 + k By doing this we have created a perfect square trinomial within the parentheses, plus a constant outside the parentheses. We express the perfect square trinomial as the square of a binomial. The function is now in the form we are seeking. continued Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -24 24

Write Functions in the Form f(x) = a(x – h)2 + k b) Graph f(x). Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 8 -25 25