Chapter 4 Chapter Content 1 Real Vector Spaces

Chapter 4 Chapter Content 1. Real Vector Spaces 2. Subspaces 3. Linear Independence 4. Basis 5. Dimension 6. Row Space, Column Space, and Nullspace 8. Rank and Nullity 9. Matrix Transformations for Rn to Rm

Definition (Vector Space) Let V be an arbitrary nonempty set of objects on which two operations are defined: addition, and multiplication by scalars. If the following axioms are satisfied by all objects u, v, w in V and all scalars k and m, then we call V a vector space and we call the objects in V vectors 1. If u and v are objects in V, then u + v is in V. 2. u + v = v + u 3. u + (v + w) = (u + v) + w 4. There is an object 0 in V, called a zero vector for V, such that 0 + u= u + 0 = u for all u in V. 5. For each u in V, there is an object -u in V, called a negative of u, such that u + (-u) = (-u) + u = 0. 6. If k is any scalar and u is any object in V, then ku is in V. 7. k (u + v) = ku + kv 8. (k + m) u = ku + mu 9. k (mu) = (km) (u) 10. 1 u = u

To Show that a Set with Two Operations is a Vector Space 1. Identify the set V of objects that will become vectors. 2. Identify the addition and scalar multiplication operations on V. 3. Verify Axioms 1(closure under addition) and 6 (closure under scalar multiplication) ; that is, adding two vectors in V produces a vector in V, and multiplying a vector in V by a scalar also produces a vector in V. 4. Confirm that Axioms 2, 3, 4, 5, 7, 8, 9 and 10 hold.

Remarks • Depending on the application, scalars may be real numbers or complex numbers. • Vector spaces in which the scalars are complex numbers are called complex vector spaces, and those in which the scalars must be real are called real vector spaces. • The definition of a vector space specifies neither the nature of the vectors nor the operations. • Any kind of object can be a vector, and the operations of addition and scalar multiplication may not have any relationship or similarity to the standard vector operations on. • The only requirement is that the ten vector space axioms be satisfied.

The Zero Vector Space Let V consist of a single object, which we denote by 0, and define 0 + 0 = 0 and k 0 = 0 for all scalars k. It’s easy to check that all the vector space axioms are satisfied. We called this the zero vector space.

Example ( Is a Vector Space) The set V = with the standard operations of addition and scalar multiplication is a vector space. (Axioms 1 and 6 follow from the definitions of the standard operations on ; the remaining axioms follow from Theorem 4. 1. 1. ) The three most important special cases of are R (the real numbers), vectors in the plane), and (the vectors in 3 -space). (the

Example (2× 2 Matrices) Show that the set V of all 2× 2 matrices with real entries is a vector space if vector addition is defined to be matrix addition and vector scalar multiplication is defined to be matrix scalar multiplication. Solution: Let and (1) we must show that u + v is a 2× 2 matrix. (2) Want to show that u + v = v + u (3) Similarly we can show that u + ( v + w ) = ( u + v )+ w. (4) Define 0 to be such that

(5) Define the negative of u to be (6) If k is any scalar and u is a 2 X 2 matrix, then such that is 2 X 2 matrix. (7)-(9) will be obtained by similar approach. (10) Thus, the set V of all 2× 2 matrices with real entries is a vector space.

Example: Given the set of all triples of real numbers ( x, y, z ) with the operations Determine if it’s a vector space under the given operation. Solution: We must check all ten properties: (1) If (x, y, z) and (x’, y’, z’) are triples of real numbers, so is (x, y, z) + (x’, y’, z’) = (x + x’, y +y’, z + z’). (2) (x, y, z) + (x’, y’, z’) = (x + x’, y + y’, z + z’)= (x’, y’, z’) + (x, y, z). (3) (x, y, z) + [(x’, y’, z’) + (x’’, y’’, z’’)] = (x, y, z) + [(x’, y’, z’) + (x’’, y’’, z’’)]. (4) There is an object 0, (0, 0, 0), such that (0, 0, 0) + (x, y, z) = (x, y, z) + (0, 0, 0)= (x, y, z). (5) For each positive real x, (-x, -y, -z) acts as the negative: (x, y, z) + (-x, -y, -z) = (-x, -y, -z) + (x, y, z) =(x, y, z)

(6) If k is a real and (x, y, z) is a triple of real numbers, then k (x, y, z) = (kx, y, z) is again a triple of real numbers. (7) k[(x, y, z) + (x’, y’, z’)] = (k(x+x’), y+y’, z+z’) = k(x, y, z) + k(x’, y’, z’) (8) (k + m) (x, y, z) = ((k + m)x, y, z) k (x, y, z) + m(x, y, z) Axiom (8) fails Thus, the set of all triples of real numbers ( x, y, z ) with the operations is NOT a vector space under the given operation.

Example. Let V = R 2 and define addition and scalar multiplication operations as follows: If u = (u 1, u 2) and v = (v 1, v 2), then define u + v = (u 1 + v 1, u 2 + v 2) and if k is any real number, then define k u = (k u 1, 0) There are values of u for which Axiom 10 fails to hold. For example, if u = (u 1, u 2) is such that u 2 ≠ 0, then 1 u = 1 (u 1, u 2) = (1 u 1, 0) = (u 1, 0) ≠ u Thus, V is not a vector space with the stated operations

Theorem 5. 1. 1 Let V be a vector space, u be a vector in V, and k a scalar; then: (a) 0 u = 0 (b) k 0 = 0 (c) (-1) u = -u (d) If k u = 0 , then k = 0 or u = 0.

4. 2 Subspaces Definition A subset W of a vector space V is called a subspace of V if W is itself a vector space under the addition and scalar multiplication defined on V. Theorem 5. 2. 1 If W is a set of one or more vectors from a vector space V, then W is a subspace of V if and only if the following conditions hold: a) If u and v are vectors in W, then u + v is in W. b) If k is any scalar and u is any vector in W , then ku is in W. Remark Theorem 5. 2. 1 states that W is a subspace of V if and only if W is a closed under addition (condition (a)) and closed under scalar multiplication (condition (b)).

Example All vectors of the form (a, 0, 0) is a subspace of R 3. • The set is closed under vector addition because (a, 0, 0) + (b, 0, 0) = (a + b, 0, 0) • It is closed under scalar multiplication because k(a, 0, 0) = (ka, 0, 0) Therefore it is a subspace of R 3.

Example (Not a Subspace) Let W be the set of all points (x, y) in R 2 such that x ≥ 0 and y ≥ 0. These are the points in the first quadrant. The set W is not a subspace of R 2 since it is not closed under scalar multiplication. For example, v = (1, 1) lines in W, but its negative (-1)v = -v = (-1, -1) does not.

Subspaces of Mnn The set of n×n diagonal matrices forms subspaces of Mnn, since each of these sets is closed under addition and scalar multiplication. The set of n×n matrices with integer entries is NOT a subspace of the vector space Mnn of n×n matrices. This set is closed under vector addition since the sum of two integers is again an integer. However, it is not closed under scalar multiplication since the product ku where k is real and a is an integer need not be an integer. Thus, the set is not a subspace.

Linear Combination Definition in 3. 1 A vector w is a linear combination of the vectors v 1, v 2, …, vr if it can be expressed in the form w = k 1 v 1 + k 2 v 2 + · · · + kr vr where k 1, k 2, …, kr are scalars. Example: Vectors in R 3 are linear combinations of i, j, and k Every vector v = (a, b, c) in R 3 is expressible as a linear combination of the standard basis vectors i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1) Since v= a(1, 0, 0) + b(0, 1, 0) + c(0, 0, 1) = a i + b j + c k

Example Consider the vectors u = (1, 2, -1) and v = (6, 4, 2) in R 3. Show that w = (9, 2, 7) is a linear combination of u and v and that w′ = (4, -1, 8) is not a linear combination of u and v. Solution. In order for w to be a linear combination of u and v, there must be scalars k 1 and k 2 such that w = k 1 u + k 2 v; (9, 2, 7) = (k 1 + 6 k 2, 2 k 1 + 4 k 2, -k 1 + 2 k 2) Equating corresponding components gives k 1 + 6 k 2 = 9 2 k 1+ 4 k 2 = 2 -k 1 + 2 k 2 = 7 Solving this system yields k 1 = -3, k 2 = 2, so w = -3 u + 2 v

Similarly, for w‘ to be a linear combination of u and v, there must be scalars k 1 and k 2 such that w'= k 1 u + k 2 v; (4, -1, 8) = k 1(1, 2, -1) + k 2(6, 4, 2) or (4, -1, 8) = (k 1 + 6 k 2, 2 k 1 + 4 k 2, -k 1 + 2 k 2) Equating corresponding components gives k 1 + 6 k 2 = 4 2 k 1+ 4 k 2 = -1 - k 1 + 2 k 2 = 8 This system of equation is inconsistent, so no such scalars k 1 and k 2 exist. Consequently, w' is not a linear combination of u and v.

Linear Combination and Spanning Theorem 5. 2. 3 If v 1, v 2, …, vr are vectors in a vector space V, then: (a) The set W of all linear combinations of v 1, v 2, …, vr is a subspace of V. (b) W is the smallest subspace of V that contain v 1, v 2, …, vr in the sense that every other subspace of V that contain v 1, v 2, …, vr must contain W.

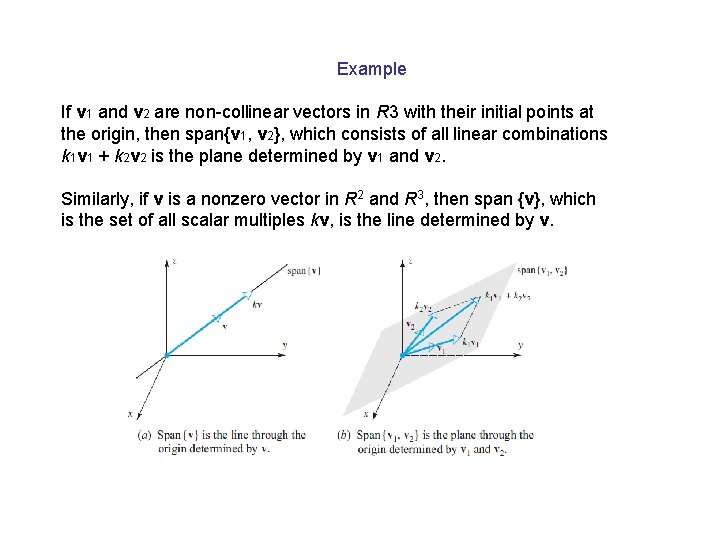
Example If v 1 and v 2 are non-collinear vectors in R 3 with their initial points at the origin, then span{v 1, v 2}, which consists of all linear combinations k 1 v 1 + k 2 v 2 is the plane determined by v 1 and v 2. Similarly, if v is a nonzero vector in R 2 and R 3, then span {v}, which is the set of all scalar multiples kv, is the line determined by v.

Example Determine whether v 1 = (1, 1, 2), v 2 = (1, 0, 1), and v 3 = (2, 1, 3) span the vector space R 3. Solution Is it possible that an arbitrary vector b = (b 1, b 2, b 3) in R 3 can be expressed as a linear combination b = k 1 v 1 + k 2 v 2 + k 3 v 3 ? b = (b 1, b 2, b 3) = k 1(1, 1, 3) + k 2(1, 0, 1) + k 3(2, 1, 3) = (k 1+k 2+2 k 3, k 1+k 3, 2 k 1+k 2+3 k 3) Or k 1 + k 2 + 2 k 3 = b 1 k 1 + k 3 = b 2 2 k 1 + k 2 + 3 k 3 = b 3 This system is consistent for all values of b 1, b 2, and b 3 if and only if the coefficient matrix has a nonzero determinant. However, det(A) = 0, so that v 1, v 2, and v 3, do not span R 3.

Solution Space of Homogeneous Systems If Ax = b is a system of the linear equations, then each vector x that satisfies this equation is called a solution vector of the system. Theorem 5. 2. 2 If Ax = 0 is a homogeneous linear system of m equations in n unknowns, then the set of solution vectors is a subspace of Rn. Remark: Theorem 5. 2. 2 shows that the solution vectors of a homogeneous linear system form a vector space, which we shall call the solution space of the system.

Theorem 4. 2. 5 If S = {v 1, v 2, …, vr} and S′ = {w 1, w 2, …, wr} are two sets of vector in a vector space V, then span{v 1, v 2, …, vr} = span{w 1, w 2, …, wr} if and only if each vector in S is a linear combination of these in S′ and each vector in S′ is a linear combination of these in S.

4. 3 Linearly Independence Definition If S = {v 1, v 2, …, vr} is a nonempty set of vector, then the vector equation k 1 v 1 + k 2 v 2 + … + krvr= 0 has at least one solution, namely k 1 = 0, k 2 = 0, … , kr = 0. If this the only solution, then S is called a linearly independent set. If there are other solutions, then S is called a linearly dependent set. Examples Given v 1 = (2, -1, 0, 3), v 2 = (1, 2, 5, -1), and v 3 = (7, -1, 5, 8). Then the set of vectors S = {v 1, v 2, v 3} is linearly dependent, since 3 v 1 + v 2 – v 3 = 0.

Example Let i = (1, 0, 0), j = (0, 1, 0), and k = (0, 0, 1) in R 3. Determine it it’s a linear independent set Solution: Consider the equation k 1 i + k 2 j + k 3 k = 0 ⇒ k 1(1, 0, 0) + k 2(0, 1, 0) + k 3(0, 0, 1) = (0, 0, 0) ⇒ (k 1, k 2, k 3) = (0, 0, 0) ⇒ The set S = {i, j, k} is linearly independent. Similarly the vectors e 1 = (1, 0, 0, …, 0), e 2 = (0, 1, 0, …, 0), …, en = (0, 0, 0, …, 1) form a linearly independent set in Rn. Remark: To check whether a set of vectors is linear independent or not, write down the linear combination of the vectors and see if their coefficients all equal zero.

Example Determine whether the vectors v 1 = (1, -2, 3), v 2 = (5, 6, -1), v 3 = (3, 2, 1) form a linearly dependent set or a linearly independent set. Solution Let the vector equation k 1 v 1 + k 2 v 2 + k 3 v 3 = 0 ⇒ k 1(1, -2, 3) + k 2(5, 6, -1) + k 3(3, 2, 1) = (0, 0, 0) ⇒ k 1 + 5 k 2 + 3 k 3 = 0 -2 k 1 + 6 k 2 + 2 k 3 = 0 3 k 1 – k 2 + k 3 = 0 ⇒ det(A) = 0 ⇒ The system has nontrivial solutions ⇒ v 1, v 2, and v 3 form a linearly dependent set

Theorems Theorem 4. 3. 1 A set with two or more vectors is: (a) Linearly dependent if and only if at least one of the vectors in S is expressible as a linear combination of the other vectors in S. (b) Linearly independent if and only if no vector in S is expressible as a linear combination of the other vectors in S. Theorem 4. 3. 2 (a) A finite set of vectors that contains the zero vector is linearly dependent. (b) A set with exactly one vector is linearly independent if and only if that vector is not the zero vector. (c) A set with exactly two vectors is linearly independent if and only if neither vector is a scalar multiple of the other. Theorem 4. 3. 3 Let S = {v 1, v 2, …, vr} be a set of vectors in Rn. If r > n, then S is linearly dependent.

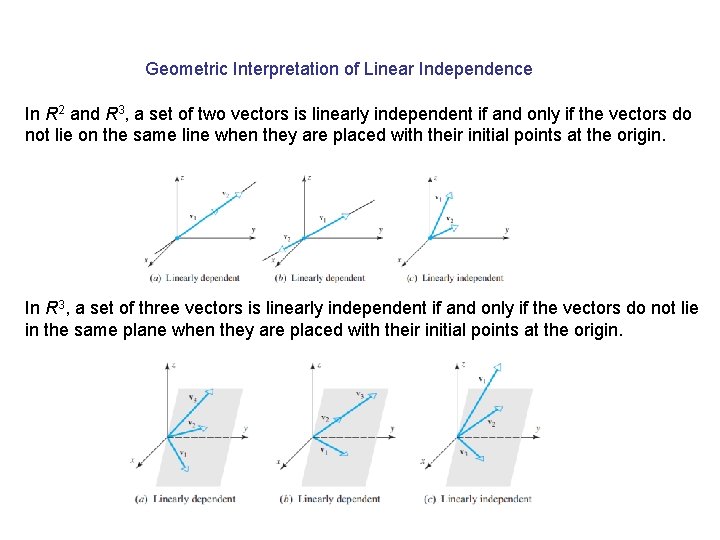
Geometric Interpretation of Linear Independence In R 2 and R 3, a set of two vectors is linearly independent if and only if the vectors do not lie on the same line when they are placed with their initial points at the origin. In R 3, a set of three vectors is linearly independent if and only if the vectors do not lie in the same plane when they are placed with their initial points at the origin.

Section 4. 4 Coordinates and Basis Definition If V is any vector space and S = {v 1, v 2, …, vn} is a set of vectors in V, then S is called a basis for V if the following two conditions hold: (a) S is linearly independent. (b) S spans V. Theorem 5. 4. 1 (Uniqueness of Basis Representation) If S = {v 1, v 2, …, vn} is a basis for a vector space V, then every vector v in V can be expressed in the form v = c 1 v 1 + c 2 v 2 + … + cnvn in exactly one way.

Coordinates Relative to a Basis If S = {v 1, v 2, …, vn} is a basis for a vector space V, and v = c 1 v 1 + c 2 v 2 + ··· + cnvn is the expression for a vector v in terms of the basis S, then the scalars c 1, c 2, …, cn, are called the coordinates of v relative to the basis S. The vector (c 1, c 2, …, cn) in Rn constructed from these coordinates is called the coordinate vector of v relative to S; it is denoted by (v)S = (c 1, c 2, …, cn) Remark: Coordinate vectors depend not only on the basis S but also on the order in which the basis vectors are written. A change in the order of the basis vectors results in a corresponding change of order for the entries in the coordinate vector.

Standard Basis for R 3 Suppose that i = (1, 0, 0), j = (0, 1, 0), and k = (0, 0, 1), then S = {i, j, k} is a linearly independent set in R 3. This set also spans R 3 since any vector v = (a, b, c) in R 3 can be written as v = (a, b, c) = a(1, 0, 0) + b(0, 1, 0) + c(0, 0, 1) = ai + bj + ck Thus, S is a basis for R 3; it is called the standard basis for R 3. Looking at the coefficients of i, j, and k, it follows that the coordinates of v relative to the standard basis are a, b, and c, so (v)S = (a, b, c) Comparing this result to v = (a, b, c), we have v = (v)S

Standard Basis for Rn If e 1 = (1, 0, 0, …, 0), e 2 = (0, 1, 0, …, 0), …, en = (0, 0, 0, …, 1), then S = {e 1, e 2, …, en} is a linearly independent set in Rn. This set also spans Rn since any vector v = (v 1, v 2, …, vn) in Rn can be written as v = v 1 e 1 + v 2 e 2 + … + vnen Thus, S is a basis for Rn; it is called the standard basis for Rn. The coordinates of v = (v 1, v 2, …, vn) relative to the standard basis are v 1 , v 2, …, vn, thus (v)S = (v 1, v 2, …, vn) As the previous example, we have v = (v)s, so a vector v and its coordinate vector relative to the standard basis for Rn are the same.

Example Let v 1 = (1, 2, 1), v 2 = (2, 9, 0), and v 3 = (3, 3, 4). Show that the set S = {v 1, v 2, v 3} is a basis for R 3. Solution: To show that the set S spans R 3, we must show that an arbitrary vector b = (b 1, b 2, b 3) can be expressed as a linear combination b = c 1 v 1 + c 2 v 2 + c 3 v 3 of the vectors in S. Let (b 1, b 2, b 3) = c 1(1, 2, 1) + c 2(2, 9, 0) + c 3(3, 3, 4) c 1 +2 c 2 +3 c 3 = b 1 2 c 1+9 c 2 +3 c 3 = b 2 c 1 +4 c 3 = b 3 Let A be the coefficient matrix So S spans R 3. , then det(A) = -1 ≠ 0

Example To show that the set S is linear independent, we must show that the only solution of c 1 v 1 + c 2 v 2 + c 3 v 3 =0 is a trivial solution. c 1 +2 c 2 +3 c 3 = 0 2 c 1+9 c 2 +3 c 3 = 0 c 1 +4 c 3 = 0 Note that det(A) = -1 ≠ 0, so S is linear independent. So S is a basis for R 3.

Example Let v 1 = (1, 2, 1), v 2 = (2, 9, 0), and v 3 = (3, 3, 4), and S = {v 1, v 2, v 3} be the basis for R 3 in the preceding example. (a) Find the coordinate vector of v = (5, -1, 9) with respect to S. (b) Find the vector v in R 3 whose coordinate vector with respect to the basis S is (v)s = (-1, 3, 2). Solution (a) We must find scalars c 1, c 2, c 3 such that v = c 1 v 1 + c 2 v 2 + c 3 v 3, or, in terms of components, (5, -1, 9) = c 1(1, 2, 1) + c 2(2, 9, 0) + c 3(3, 3, 4) c 1 +2 c 2 +3 c 3 = 5 2 c 1+9 c 2 +3 c 3 = -1 c 1 +4 c 3 = 9 Solving this, we obtaining c 1 = 1, c 2 = -1, c 3 = 2. Therefore, (v)s = (1, -1, 2).

Solution (b) Using the definition of the coordinate vector (v)s, we obtain v = (-1)v 1 + 3 v 2 + 2 v 3 = (11, 31, 7).

Finite-Dimensional Definition A nonzero vector space V is called finite-dimensional if it contains a finite set of vector {v 1, v 2, …, vn} that forms a basis. If no such set exists, V is called infinite-dimensional. In addition, we shall regard the zero vector space to be finite-dimensional. Example The vector space Rn is finite-dimensional.

4. 5 Dimension Theorem 4. 5. 2 Let V be a finite-dimensional vector space and {v 1, v 2, …, vn} any basis. (a) If a set has more than n vector, then it is linearly dependent. (b) If a set has fewer than n vector, then it does not span V. Which can be used to prove the following theorem. Theorem 4. 5. 1 All bases for a finite-dimensional vector space have the same number of vectors.

Dimension Definition The dimension of a finite-dimensional vector space V, denoted by dim(V), is defined to be the number of vectors in a basis for V. In addition, we define the zero vector space to have dimension zero. Example: dim(Rn) = n [The standard basis has n vectors] dim(Mmn) = mn [The standard basis has mn vectors]

Example Determine a basis for and the dimension of the solution space of the homogeneous system 2 x 1 + 2 x 2 – x 3 + x 5 = 0 -x 1 - x 2 + 2 x 3 – 3 x 4 + x 5 = 0 x 1 + x 2 – 2 x 3 – x 5 = 0 x 3+ x 4 + x 5 = 0 Solution: By Gauss-Jordan Elimination method, we have Thus, x 1+x 2+x 5=0, x 3+x 5=0, x 4=0. Solving for the leading variables yields the general solution of the given system: x 1 = -s-t, x 2 = s, x 3 = -t, x 4 = 0, x 5 = t

Solution Therefore, the solution vectors can be written as Which shows that the vectors span the solution space. Since they are also linearly independent, {v 1, v 2} is a basis, and the solution space is two-dimensional.

Some Fundamental Theorems Theorem 4. 5. 3 (Plus/Minus Theorem) Let S be a nonempty set of vectors in a vector space V. (a) If S is a linearly independent set, and if v is a vector in V that is outside of span(S), then the set S ∪ {v} that results by inserting v into S is still linearly independent. (b) If v is a vector in S that is expressible as a linear combination of other vectors in S, and if S – {v} denotes the set obtained by removing v from S, then S and S – {v} span the same space; that is, span(S) = span(S – {v}) Theorem 4. 5. 4 If V is an n-dimensional vector space, and if S is a set in V with exactly n vectors, then S is a basis for V if either S spans V or S is linearly independent.

Theorems Theorem 4. 5. 5 Let S be a finite set of vectors in a finite-dimensional vector space V. (a) If S spans V but is not a basis for V, then S can be reduced to a basis for V by removing appropriate vectors from S. (b) If S is a linearly independent set that is not already a basis for V, then S can be enlarged to a basis for V by inserting appropriate vectors into S. Theorem 4. 5. 6 If W is a subspace of a finite-dimensional vector space V, then (a) W is finite-dimensional. (b) dim(W) ≤ dim(V); (c) W = V if and only if dim(W) = dim(V).

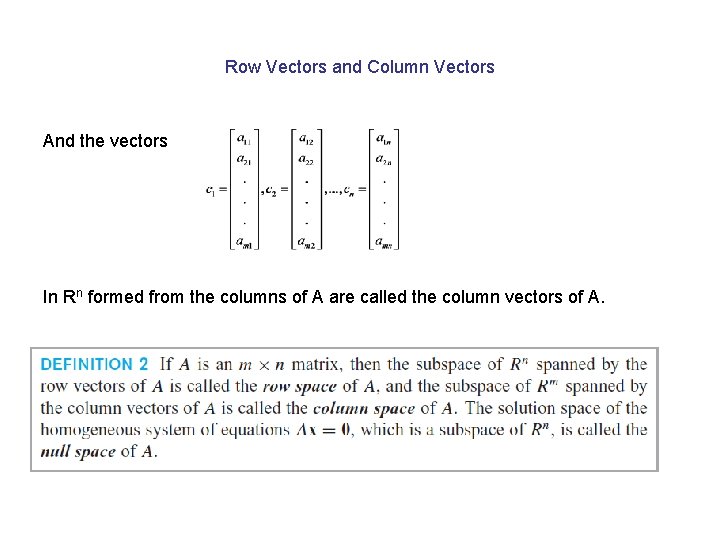
Section 4. 7 Row Space, Column Space, and Nullsapce Definition. For an mxn matrix The vectors in Rn formed from the rows of A are called the row vectors of A,

Row Vectors and Column Vectors And the vectors In Rn formed from the columns of A are called the column vectors of A.

Nullspace Theorem Elementary row operations do not change the nullspace of a matrix. Example Find a basis for the nullspace of The nullspace of A is the solution space of the homogeneous system Ax=0. 2 x 1 + 2 x 2 – x 3 + x 5 = 0 -x 1 - x 2 + 2 x 3 – 3 x 4 + x 5 = 0 x 1 + x 2 – 2 x 3 – x 5 = 0 x 3+ x 4 + x 5 = 0.

Nullspace Cont. Then by the previous example, we know Form a basis for this space.

Theorems Theorem Elementary row operations do not change the row space of a matrix. Note: Elementary row operations DO change the column space of a matrix. However, we have the following theorem Theorem If A and B are row equivalent matrices, then (a) A given set of column vectors of A is linearly independent if and only if the corresponding column vectors of B are linearly independent. (b) A given set of column vectors of A forms a basis for the column space of A if and only if the corresponding column vectors of B form a basis for the column space of B.

Theorems Cont. Theorem If a matrix R is in row-echelon form, then the row vectors with the leading 1’s (the nonzero row vectors) form a basis for the row space of R, and the column vectors with the leading 1’s of the row vectors form a basis for the column space of R.

Example Find bases for the row and column spaces of Solution. Since elementary row operations do not change the row space of a matrix, we can find a basis for the row space of A by finding a basis for the row space of any row-echelon form of A.

Example By Theorem, the nonzero row vectors of R form a basis for the row space of R and hence form a basis for the row space of A. These basis vectors are Note that A ad R may have different column spaces, but from Theorem that if we can find a set of column vectors of R that forms a basis for the column space of R, then the corresponding column vectors of A will form a basis for the column space of A.

Example Note Form a basis for the column space of R; thus the corresponding column vectors of A, Form a basis for the column space of A.

Section 4. 8 Rank and Nullity Theorem If A is any matrix, then the row space and column space of A have the same dimension. Definition The common dimension of the row space and column space of a matrix A is called the rank of A and is denoted by rank(A); the dimension of the nullspace of A is called the nullity of A and is denoted by nullity(A).

Example Find the rank and nullity of the matrix Solution. The reduced row-echelon form of A is

Example Since there are two nonzero rows (or, equivalently, two leading 1’s), the row space and column space are both two-dimensional, so rank(A)=2. To find the nullity of A, we must find the dimension of the solution space of the linear system Ax=0. This system can be solved by reducing the augmented matrix to reduced row-echelon form. The corresponding system of equations will be X 1 -4 x 3 -28 x 4 -37 x 5+13 x 6=0 X 2 -2 x 3 -12 x 4 -16 x 5+5 x 6=0 Solving for the leading variables, we have x 1=4 x 3+28 x 4+37 x 5 -13 x 6 X 2=2 x 3+12 x 4 +16 x 5 -5 x 6 It follows that the general solution of the system is

Example Cont. x 1=4 r+28 s+37 t-13 u X 2=2 r+12 s +16 t-5 u X 3=r X 4=s X 5=t X 6=u Equivalently, Because the four vectors on the right side of the equation form a basis for the solution space, nullity(A)=4.

Theorems Theorem If A is any matrix, then rank(A)=rank(AT). Theorem (Dimension Theorem for Matrices) If A is a matrix with n columns, then Rank(A)+nullity(A)=n Theorem If A is an mxn matrix, then (a) rank(A)= the number of leading variables in the solution of Ax=0. (b) nullity(A)= the number of parameters in the general solution of Ax=0.

Theorems Theorem (Equivalent Statements) If A is an nxn matrix, and if TA: Rn is multiplication by A, then the following are equivalent. (a) A is invertible. (b) Ax=0 has only the trivial solution. (c) The reduced row-echelon form of A is In. (d) A is expressed as a product of elementary matrices. (e) Ax=b is consistent for every nx 1 matrix b. (f) Ax=b has exactly one solution for every nx 1 matrix b. (g) Det(A) 0. (h) The range of TA is Rn. (i) TA is one-to-one. (j) The column vectors of A are linearly independent.

Theorem Cont. (k) (l) (m) (n) (o) (p) (q) The row vectors of A are linearly independent. The column vectors of A span Rn. The row vectors of A span Rn. The column vectors of A form a basis for Rn. The row vectors of A form a basis for Rn. A has rank n. A has nullity 0.

4. 9 Transformations from Functions from to to R A function is a rule f that associates with each element in a set A one and only one element in a set B. If f associates the element b with the element a, then we write b = f(a) and say that b is the image of a under f or that f(a) is the value of f at a. The set A is called the domain of f and the set B is called the codomain of f. The subset of B consisting of all possible values for f as a varies over A is called the range of f.

Function from to Here, we will be concerned exclusively with transformations from Rn to Rm. Suppose f 1, f 2, …, fm are real-valued functions of n real variables, say w 1 = f 1(x 1, x 2, …, xn) w 2 = f 2(x 1, x 2, …, xn) … wm = fm(x 1, x 2, …, xn) These m equations assign a unique point (w 1, w 2, …, wm) in Rm to each point (x 1, x 2, …, xn) in Rn and thus define a transformation from Rn to Rm. If we denote this transformation by T: Rn → Rm, then T (x 1, x 2, …, xn) = (w 1, w 2, …, wm)

Example: The equations Defines a transformation With this transformation, the image of the point (x 1, x 2) is Thus, for example, T(1, -2)=(-1, -6, -3)

Linear Transformations from to A linear transformation (or a linear operator if m = n) T: defined by equations of the form → is or or w = Ax The matrix A = [aij] is called the standard matrix for the linear transformation T, and T is called multiplication by A.

Example: If the linear transformation Find the standard matrix for T, and calculate Solution: T can be expressed as So the standard matrix for T is is defined by the equations

Furthermore, Or

Remarks Notations: If it is important to emphasize that A is the standard matrix for T. We denote the linear transformation T: → by TA: →. Thus, TA(x) = Ax We can also denote the standard matrix for T by the symbol [T], or T(x) = [T]x Remark: We have establish a correspondence between m×n matrices and linear transformations from to : To each matrix A there corresponds a linear transformation TA (multiplication by A), and to each linear transformation T: → , there corresponds an m×n matrix [T] (the standard matrix for T).

Properties of Matrix Transformations The following theorem lists four basic properties of matrix transformations that follow from the properties of matrix multiplication. Theorem 4. 9. 2 If TA: Rn Rm and TB: Rn Rm are matrix multiplications, and if TA(x)=TB(x) for every vector x in Rn, then A=B.

Examples Zero Transformation from to If 0 is the m×n zero matrix and 0 is the zero vector in vector x in T 0(x) = 0 x = 0 So multiplication by zero maps every vector in. . We call T 0 the zero transformation from , then for every into the zero vector in to. Identity operator on If I is the n×n identity, then for every vector in T I(x) = Ix = x So multiplication by I maps every vector in identity operator on. into itself. We call TI the

A Procedure for Finding Standard Matrices

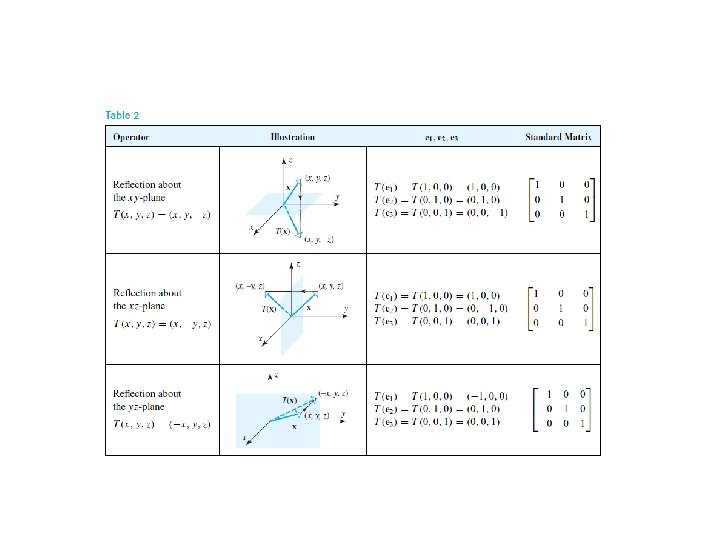
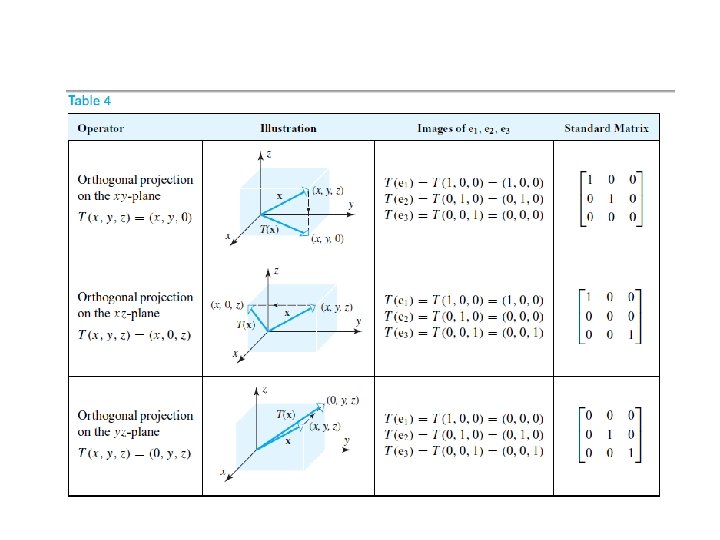
Reflection Operators In general, operators on and that map each vector into its symmetric image about some line or plane are called reflection operators. Such operators are linear.

Projection Operators In general, a projection operator (or more precisely an orthogonal projection operator) on or is any operator that maps each vector into its orthogonal projection on a line or plane through the origin. The projection operators are linear.

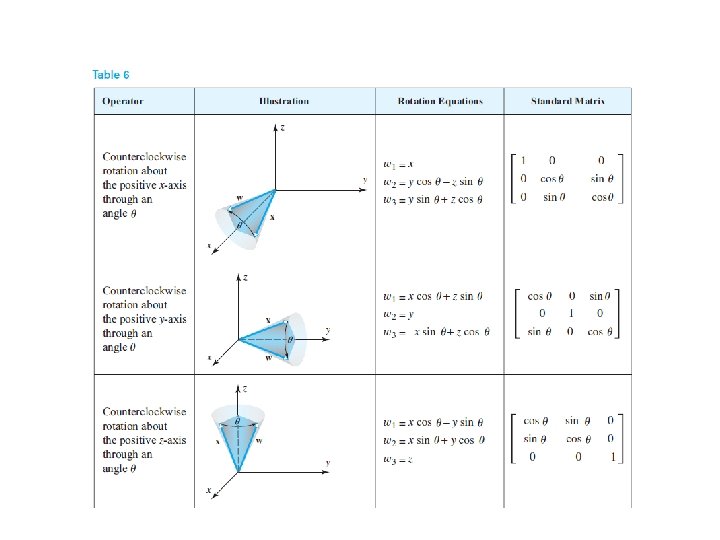
Rotation Operators An operator that rotate each vector in rotation operator on. through a fixed angle θ is called a

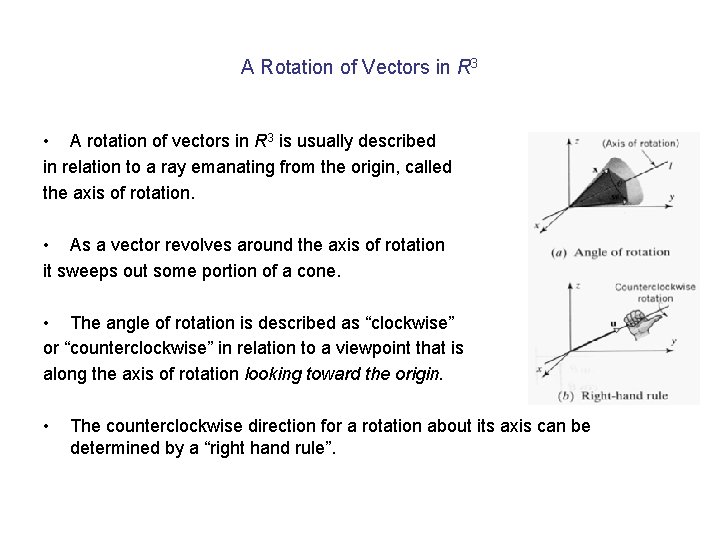
A Rotation of Vectors in R 3 • A rotation of vectors in R 3 is usually described in relation to a ray emanating from the origin, called the axis of rotation. • As a vector revolves around the axis of rotation it sweeps out some portion of a cone. • The angle of rotation is described as “clockwise” or “counterclockwise” in relation to a viewpoint that is along the axis of rotation looking toward the origin. • The counterclockwise direction for a rotation about its axis can be determined by a “right hand rule”.

Example: Use matrix multiplication to find the image of the vector (1, 1) when it is rotated through an angle of 30 degree ( ) Solution: the image of the vector So is

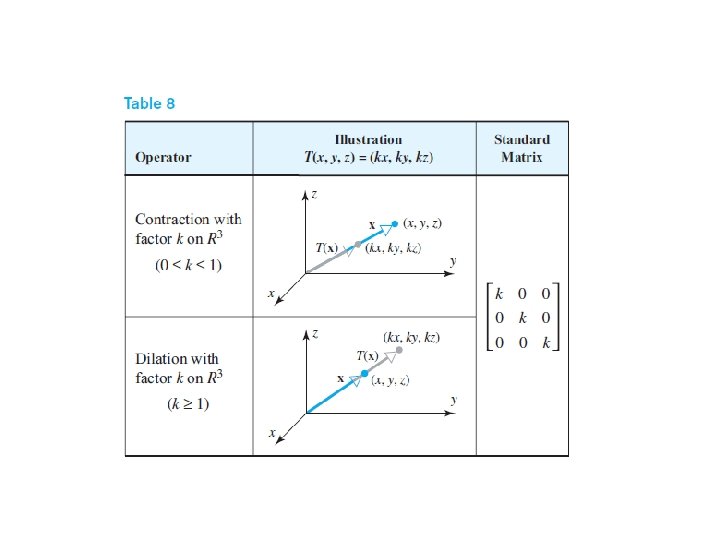
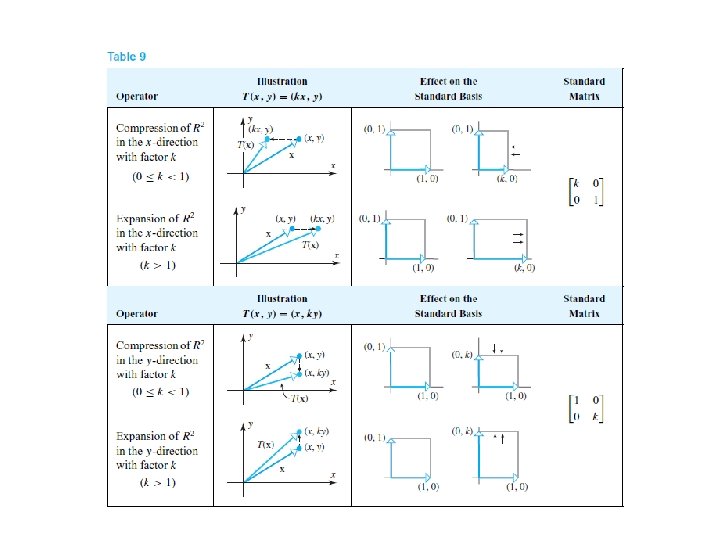
Dilation and Contraction Operators If k is a nonnegative scalar, the operator on or is called a contraction with factor k if 0 ≤ k ≤ 1 and a dilation with factor k if k ≥ 1.

Expansion and Compressions In a dilation or contraction of R 2 or R 3, all coordinates are multiplied by a factor k. If only one of the coordinates is multiplied by k, then the resulting operator is called an expansion or compression with factor k.

Shears A matrix operator of the form T(x, y)=(x+ky, y) is called the shear in the xdirection with factor k. Similarly, a matrix operator of the form T(x, y)=(x, y+kx) is called the shear in the y-direction with factor k.

4. 10 Properties of Matrix Transformations Compositions of Linear Transformations If TA : → and TB : → are linear transformations, then for each x in one can first compute TA(x), which is a vector in , and TB then one can compute TB(TA(x)), which is a vector in. Thus, the application of TA followed by TB produces a transformation from to. This transformation is called the composition of TB with TA and is denoted by. Thus The composition The standard matrix for is linear since is BA. That is,

Remark: captures an important idea: Multiplying matrices is equivalent to composing the corresponding linear transformations in the right-to-left order of the factors. Alternatively, If the standard matrix for the composition of T 2 and T 1, we have are linear transformations, then because is the product of the standard matrices

Example: Find the standard matrix for the linear operator that first reflects A vector about the y-axis, then reflects the resulting vector about the x-axis. Solution: The linear transformation T can be expressed as the composition Where T 1 is the reflection about the y-axis, and T 2 is the reflection about The x-axis. Sine the standard matrix for T is Which is called the reflection about the origin.

Note: the composition is NOT commutative. Example: Let be the reflection operator about the line y=x, and let be the orthogonal projection on the y-axis. Then Thus, have different effects on a vector x.

One–to-One Matrix Transformations

Linearity Properties

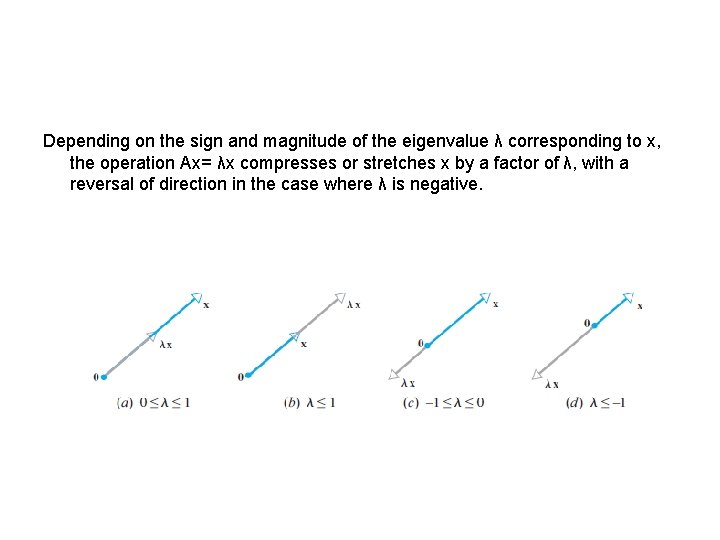
Section 5. 1 Eigenvalue and Eigenvector In general, the image of a vector x under multiplication by a square matrix A differs from x in both magnitude and direction. However, in the special case where x is an eigenvector of A, multiplication by A leaves the direction unchanged.

Depending on the sign and magnitude of the eigenvalue λ corresponding to x, the operation Ax= λx compresses or stretches x by a factor of λ, with a reversal of direction in the case where λ is negative.

Computing Eigenvalues and Eigenvectors Example. Find the eigenvalues of the matrix Solution. This shows that the eigenvalues of A are λ=3 and λ=-1.

Finding Eigenvectors and Bases for Eigenspaces Since the eigenvectors corresponding to an eigenvalue λ of a matrix A