Engineering Analysis Chapter 3 Vector Spaces 1 Vector













































- Slides: 49

Engineering Analysis Chapter 3 Vector Spaces 1

Vector Spaces The operations of addition and scalar multiplication are used in many diverse contexts in mathematics. Regardless of the context, however, these operations usually obey the same set of algebraic rules. Thus, a general theory of mathematical systems involving addition and scalar multiplication will be applicable to many areas in mathematics. Mathematical systems of this form are called vector spaces or linear spaces. In this chapter, the definition of a vector space is given and some of the general theory of vector spaces is developed. 2

3. 1 Definition and Examples 3

3. 1 Definition and Examples 4

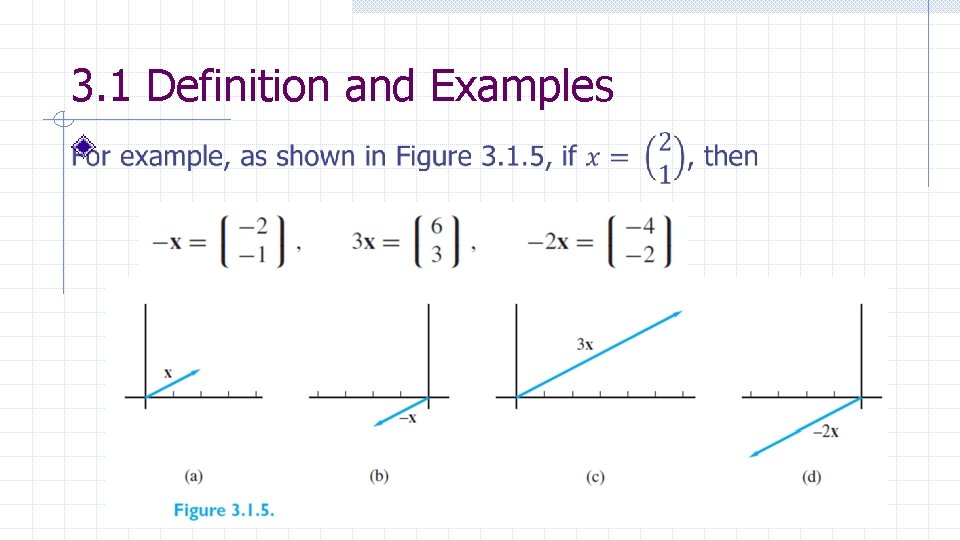
3. 1 Definition and Examples For example, as shown in Figure 3. 1. 5, if 5

3. 1 Definition and Examples 6

3. 1 Definition and Examples The sum of two vectors Note that, if v is placed at the terminal point of u, then u + v is represented by the directed line segment from the initial point of u to the terminal point of v (Figure 3. 1. 6). 7

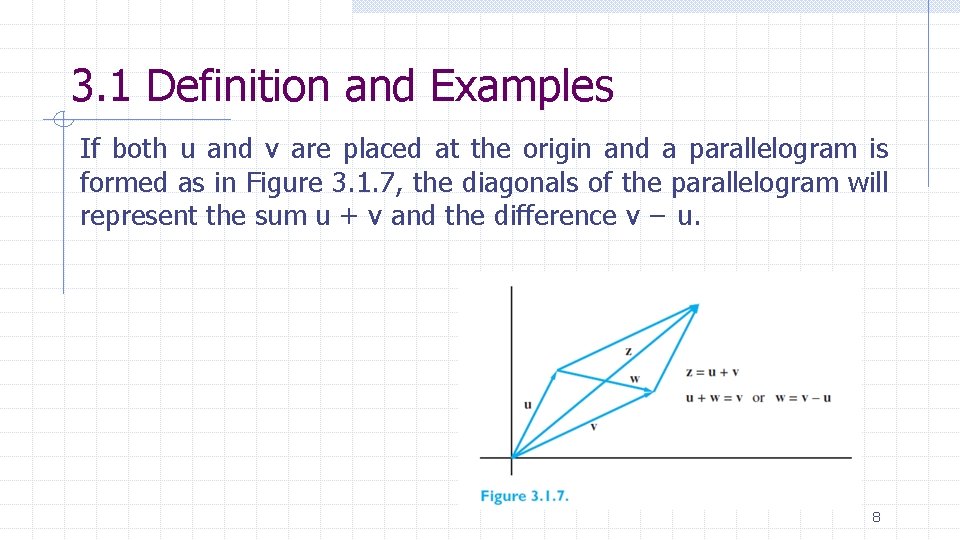
3. 1 Definition and Examples If both u and v are placed at the origin and a parallelogram is formed as in Figure 3. 1. 7, the diagonals of the parallelogram will represent the sum u + v and the difference v − u. 8

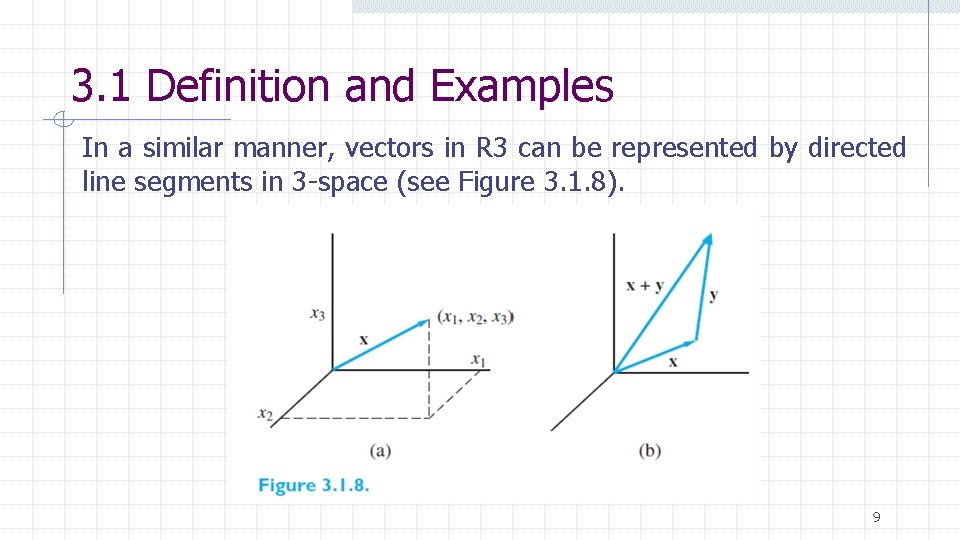
3. 1 Definition and Examples In a similar manner, vectors in R 3 can be represented by directed line segments in 3 -space (see Figure 3. 1. 8). 9

3. 1 Definition and Examples We will refer to the set V as the universal set for the vector space. Its elements are called vectors and are usually denoted by boldface letters such as u, v, w, x, y, and z. The term scalar will generally refer to a real number, although in some cases it will be used to refer to complex numbers. Scalars will generally be represented by lowercase italic letters such as a, b, and c or lowercase Greek letters such as α, β, and γ. 10

3. 1 Definition and Examples An important component of the definition is the closure properties of the two operations. These properties can be summarized as follows: C 1. If x ∈ V and α is a scalar, then αx ∈ V. C 2. If x, y ∈ V, then x + y ∈ V. To illustrate the necessity of the closure properties, consider the following example: Let W = {(a, 1) | a real} with addition and scalar multiplication defined in the usual way. The elements (3, 1) and (5, 1) are in W, but the sum (3, 1) + (5, 1) = (8, 2) is not an element of W. The operation + is not really an operation on the set W because property C 2 fails to hold. Similarly, scalar multiplication is not defined on W, because property C 1 fails to hold. The set W, together with the operations of addition and scalar multiplication, is not a vector space. 11

3. 1 Definition and Examples Theorem 3. 1. 1 If V is a vector space and x is any element of V, then (i) 0 x = 0. (ii) x + y = 0 implies that y = −x (i. e. , the additive inverse of x is unique). (iii) (− 1)x = −x. 12

3. 2 Subspaces • Given a vector space V, it is often possible to form another vector space by taking a subset S of V and using the operations of V. Since V is a vector space, the operations of addition and scalar multiplication always produce another vector in V. • For a new system using a subset S of V as its universal set to be a vector space, the set S must be closed under the operations of addition and scalar multiplication. • That is, the sum of two elements of S must always be an element of S, and the product of a scalar and an element of S must always be an element of S. 13

3. 2 Subspaces EXAMPLE 1 If Let is any element of S and α is any scalar, then is also an element of S. If are any two elements of S, then their sum is also an element of S. 14

3. 2 Subspaces Definition To show that a subset S of a vector space forms a subspace, we must show that S is nonempty and that the closure properties (i) and (ii) in the definition are satisfied. Since every subspace must contain the zero vector, we can verify that S is nonempty by showing that 0 ∈ S. 15

3. 2 Subspaces Condition (i) says that S is closed under scalar multiplication. That is, whenever an element of S is multiplied by a scalar, the result is an element of S. Condition (ii) says that S is closed under addition. That is, the sum of two elements of S is always an element of S. Thus, if we use the operations from V and the elements of S, to do arithmetic, then we will always end up with elements of S. A subspace of V, then, is a subset S that is closed under the operations of V. 16

3. 2 Subspaces EXAMPLE 2 Let S = {(x 1, x 2, x 3)T | x 1 = x 2}. The set S is nonempty since 0 = (0, 0, 0)T ∈ S. To show that S is a subspace of R 3, we need to verify that the two closure properties hold: (i) If x = (a, a, b)T is any vector in S, then αx = (αa, αb)T ∈ S (ii) If (a, a, b)T and (c, c, d)T are arbitrary elements of S, then (a, a, b)T + (c, c, d)T = (a + c, b + d)T ∈ S Since S is nonempty and satisfies the two closure conditions, it follows that S is a subspace of R 3. 17

3. 2 Subspaces EXAMPLE 3 Let If either of the two conditions in the definition fails to hold, then S will not be a subspace. In this case the first condition fails since Therefore, S is not a subspace. Actually, both conditions fail to hold. S is not closed under addition, since 18

3. 2 Subspaces EXAMPLE 4 Let The set S is nonempty, since O (the zero matrix) is in S. To show that S is a subspace, we verify that the closure properties are satisfied: (i) If A ∈ S, then A must be of the form and hence Since the (2, 1) entry of αA is the negative of the (1, 2) entry, αA ∈ S. (ii) If A, B ∈ S, then they must be of the form It follows that Hence A + B ∈ S. 19

3. 2 Subspaces 20

3. 2 Subspaces 21

3. 2 Subspaces (C) W 3 is the y-axis in the xy-plane (see Figure). To see whether W 3 subspace, let is a be vectors in W 3. Then which is in W 3, condition (i) in Definition holds. Moreover, if c is a scalar, 22

3. 2 Subspaces The Null Space of a Matrix Let A be an m × n matrix. Let N(A) denote the set of all solutions to the homogeneous system Ax = 0. Thus, We claim that N(A) is a subspace of Rn. Clearly, 0 ∈ N(A), so N(A) is nonempty. If x ∈ N(A) and α is a scalar, then and hence αx ∈ N(A). If x and y are elements of N(A), then 23

3. 2 Subspaces EXAMPLE 6 Determine N(A) if Solution Using Gauss–Jordan reduction to solve Ax = 0, we obtain The reduced row echelon form involves two free variables, x 3 and x 4 24

3. 2 Subspaces is a solution of Ax = 0. The vector space N(A) consists of all vectors of the form 25

3. 2 Subspaces The Span of a Set of Vectors Definition Let v 1, v 2, . . . , vn be vectors in a vector space V. A sum of the form α 1 v 1 + α 2 v 2 + · · · + αn vn, where α 1, . . . , αn are scalars, is called a linear combination of v 1, v 2, . . . , vn. The set of all linear combinations of v 1, v 2, . . . , vn is called the span of v 1, . . . , vn. The span of v 1, . . . , vn will be denoted by Span(v 1, . . . , vn). EXAMPLE 7 26

3. 2 Subspaces The subspace can be interpreted geometrically as the set of all vectors in 3 space that lie in the x 1 x 2 -plane (see Figure 3. 2. 1). The span of e 1, e 2, e 3 is the set of all vectors of the form Theorem 3. 2. 1 If v 1, v 2, . . . , vn are elements of a vector space V, then Span(v 1, v 2, . . . , vn) is a subspace of V. 27

3. 2 Subspaces Spanning Set for a Vector Space Definition The set {v 1, . . . , vn} is a spanning set for V if and only if every vector in V can be written as a linear combination of v 1, v 2, . . . , vn. 28

3. 2 Subspaces Solution To determine whether a set spans R 3, we must determine whether an arbitrary vector (a, b, c)T in R 3 can be written as a linear combination of the vectors in the set. In part (a), it is easily seen that (a, b, c)T can be written as This leads to the system of equations 29

3. 2 Subspaces Since the coefficient matrix of the system is nonsingular, the system has a unique solution. In fact, we find that Thus, 30

3. 2 Subspaces Part (d) can be done in the same manner as part (b). If then In this case, however, the coefficient matrix is singular. Gaussian elimination will yield a system of the form If then the system is inconsistent. Hence, for most choices of a, b, and c, it is impossible to express (a, b, c)T as a linear combination of (1, 2, 4)T , (2, 1, 3)T , and (4, − 1, 1)T. The vectors do not span R 3. 31

3. 3 Linear Independence • In this section, we look more closely at the structure of vector spaces. To begin with, we restrict ourselves to vector spaces that can be generated from a finite set of elements. Each vector in the vector space can be built up from the elements in this generating set using only the operations of addition and scalar multiplication. • The generating set is usually referred to as a spanning set. In particular, it is desirable to find a minimal spanning set. By minimal we mean a spanning set with no unnecessary elements • To see how to find a minimal spanning set, it is necessary to consider how the vectors in the collection depend on each other. • Consequently, we introduce the concepts of linear dependence and linear independence. These simple concepts provide the keys to understanding the structure of vector spaces. 32

3. 3 Linear Independence Any linear combination of x 1, x 2, and x 3 can be reduced to a linear combination of x 1 and x 2: Thus, Equation (1) can be rewritten in the form 33

3. 3 Linear Independence Since three coefficients in (2) are nonzero, we could solve for any vector in terms of the other two: It follows that: Span(x 1, x 2, x 3) = Span(x 1, x 2) Because of the dependency relation (2), the subspace S can be represented as the span of any two of the given vectors. In contrast, no such dependency relationship exists between x 1 and x 2. Indeed, if there were scalars c 1 and c 2, not both 0, such that then we could solve for one of the vectors in terms of the other: 34

3. 3 Linear Independence However, neither of the two vectors in question is a multiple of the other. Therefore, Span(x 1) and Span(x 2) are both proper subspaces of Span(x 1, x 2), and the only way that (3) can hold is if c 1 = c 2 = 0. We can generalize this example by making the following observations: I. If v 1, v 2, . . . , vn span a vector space V and one of these vectors can be written as a linear combination of the other n − 1 vectors, then those n − 1 vectors span V. II. Given n vectors v 1, . . . , vn, it is possible to write one of the vectors as a linear combination of the other n − 1 vectors if and only if there exist scalars c 1, . . . , cn, not all zero, such that 35

3. 3 Linear Independence Definition EXAMPLE 1 36

3. 3 Linear Independence Definition EXAMPLE 2 37

3. 3 Linear Independence Geometric Interpretation If x and y are linearly dependent in R 2, then where c 1 and c 2 are not both 0. If, say, c 1 ≠ 0, we can write 38

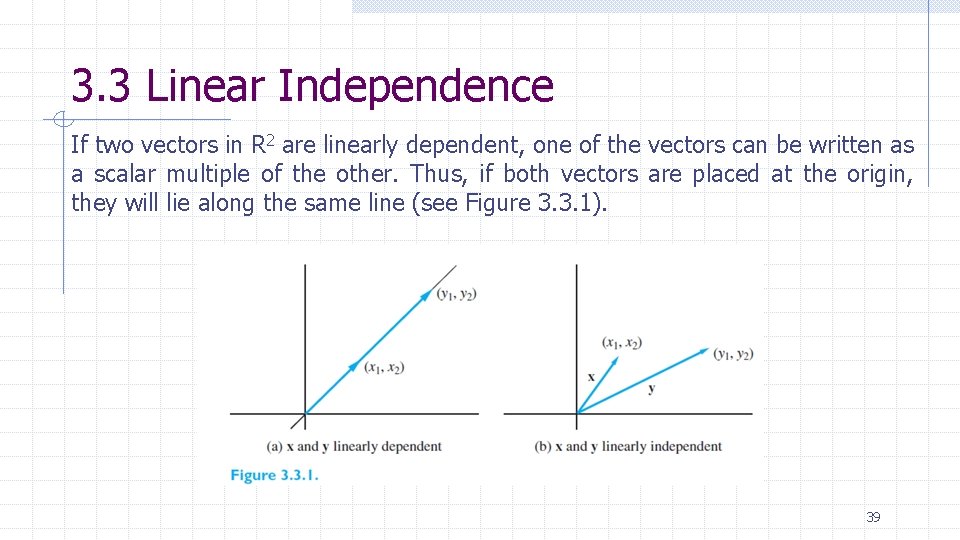
3. 3 Linear Independence If two vectors in R 2 are linearly dependent, one of the vectors can be written as a scalar multiple of the other. Thus, if both vectors are placed at the origin, they will lie along the same line (see Figure 3. 3. 1). 39

3. 3 Linear Independence EXAMPLE 3 Which of the following collections of vectors are linearly independent in R 3? Solution (a) These three vectors are linearly independent. To verify this, we must show that the only way for is if the scalars c 1, c 2, c 3 are all zero. Above Equation can be written as a linear system with unknowns c 1, c 2, c 3: 40

3. 3 Linear Independence The only solution of this system is c 1 = 0, c 2 = 0, c 3 = 0. (b) If then so c 1 = c 2 = 0. Therefore, the two vectors are linearly independent. 41

3. 3 Linear Independence (c) If 42

3. 3 Linear Independence The set S = {v 1, v 2, v 3} of vectors in R 3 is linearly independent if the only solution of c 1 v 1 + c 2 v 2 + c 3 v 3 = 0, is c 1 , c 2 , c 3 = 0 Otherwise (i. e. , if a solution with at least some nonzero values exists), S is linearly dependent. Solution Step 1: Set up a homogeneous system of equations The matrix equation above is equivalent to the following homogeneous system of equations 43

3. 3 Linear Independence Step 2: Transform the coefficient matrix of the system to the reduced row echelon form 44

3. 3 Linear Independence 45

3. 3 Linear Independence Step 3: Interpret the reduced row echelon form • the trivial solution only (meaning that S is linearly independent), or • the trivial solution as well as nontrivial ones (S is linearly dependent) now which corresponds to the system The leading entries have been highlighted in yellow. Since some columns do not contain leading entries, then the system has nontrivial solutions, so that some of the values c 1, c 2, c 3 solving may be nonzero. Therefore the set S = {v 1, v 2, v 3} is linearly dependent 46

3. 3 Linear Independence Notice in Example 3, parts (a) and (c), that it was necessary to solve a 3 × 3 system to determine whether the three vectors were linearly independent. In part (a), where the coefficient matrix was nonsingular, the vectors were linearly independent, while in part (c), where the coefficient matrix was singular, the vectors were linearly dependent Theorem 3. 3. 1 Let x 1, x 2, . . . , xn be n vectors in Rn and let X = (x 1, . . . , xn). The vectors x 1, x 2, . . . , xn will be linearly dependent if and only if X is singular 47

3. 3 Linear Independence EXAMPLE 4 48

3. 3 Linear Independence EXAMPLE 5 Given To determine whether the vectors are linearly independent, we reduce the system to row echelon form: Since the echelon form involves a free variable c 3, there are nontrivial solutions and hence the vectors must be linearly dependent. 49
 Block diagonal matrix
Block diagonal matrix Isomorphism of vector spaces
Isomorphism of vector spaces Notasi vektor adalah
Notasi vektor adalah How to find a unit vector
How to find a unit vector Cosenos directores de un vector
Cosenos directores de un vector Vector resolution examples
Vector resolution examples Site:slidetodoc.com
Site:slidetodoc.com Twinspace etwinning.net
Twinspace etwinning.net Hardened magma squeezed into vertical spaces between rocks
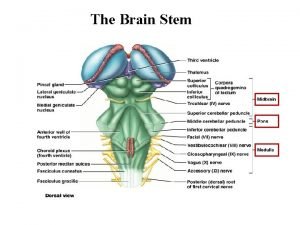
Hardened magma squeezed into vertical spaces between rocks Brain stem
Brain stem Ollies raleigh
Ollies raleigh Mesiognathic
Mesiognathic Spaces of the neck
Spaces of the neck Fascial space of hand
Fascial space of hand Dorsal subaponeurotic space
Dorsal subaponeurotic space Incisal labiality
Incisal labiality Ros smith
Ros smith Sample complexity for finite hypothesis spaces
Sample complexity for finite hypothesis spaces Canine relationship
Canine relationship Hot potato voice
Hot potato voice Vector space properties
Vector space properties Spaces between particles of liquid
Spaces between particles of liquid Types of performance space
Types of performance space Objectives of dewatering
Objectives of dewatering Kennedy 1 mod 2
Kennedy 1 mod 2 Ancillary spaces
Ancillary spaces Spaces cite multimedia
Spaces cite multimedia Qualcomm snapdragon developer unreal engine unityverge
Qualcomm snapdragon developer unreal engine unityverge Imago mundi eliade
Imago mundi eliade New yorkers spaces homes
New yorkers spaces homes Complete the spaces with the present continuous tense
Complete the spaces with the present continuous tense Good boys do fine always
Good boys do fine always Invited spaces of participation
Invited spaces of participation Intersection of half spaces
Intersection of half spaces Gwam typing
Gwam typing Croquis blouse
Croquis blouse Prevertebral vessels
Prevertebral vessels Maniobra de yódice-sanmartino
Maniobra de yódice-sanmartino Fill in the spaces using a or an
Fill in the spaces using a or an Lingual tonsil
Lingual tonsil Characteristics of confined space
Characteristics of confined space Confined spaces
Confined spaces Confined spaces
Confined spaces Caves are natural underground spaces
Caves are natural underground spaces The oval shaped symbols placed on staff
The oval shaped symbols placed on staff Tenor clef lines and spaces
Tenor clef lines and spaces Sample spaces
Sample spaces Site:slidetodoc.com
Site:slidetodoc.com Representing sample spaces
Representing sample spaces Simon berkovich
Simon berkovich