Lecture 8 Vector Space Last Time Vector Spaces

Lecture 8 Vector Space Last Time - Vector Spaces and Applications - Subspaces of Vector Spaces - Spanning Sets and Linear Independence Elementary Linear Algebra R. Larsen et al. (5 Edition) TKUEE翁慶昌-NTUEE SCC_11_2007

Lecture 8: Vector Space Today n Spanning Sets and Linear Independence (Cont. ) n Basis and Dimension n Rank of a Matrix and Systems of Linear Equations Reading Assignment: Secs 4. 4 - 4. 6 Next Time n Midterm Exam (14: 20 – 16: 00, 11/16) n Scope: Chapters 1 -4. 6 n Homework-like problems: 80% n In-class Q&A type and advanced problems: 20% 8 -2

Today n Spanning Sets and Linear Independence (Cont. ) n Basis and Dimension n Rank of a Matrix and Systems of Linear Equations 8 -3

What Have You Actually Learned about Vector Space? 8 -4

4. 4 Spanning Sets and Linear Independence § Linear combination: 8 -5

§ the span of a set: span (S) If S={v 1, v 2, …, vk} is a set of vectors in a vector space V, then the span of S is the set of all linear combinations of the vectors in S, § a spanning set of a vector space: If every vector in a given vector space can be written as a linear combination of vectors in a given set S, then S is called a spanning set of the vector space. 8 -6

§ Notes: 8 -7

§ Thm 4. 7: (Span(S) is a subspace of V) If S={v 1, v 2, …, vk} is a set of vectors in a vector space V, then (a) span (S) is a subspace of V. (b) span (S) is the smallest subspace of V that contains S. (Every other subspace of V that contains S must contain span (S). ) 8 -8

§ Linear Independent (L. I. ) and Linear Dependent (L. D. ): : a set of vectors in a vector space V 8 -9

§ Notes: 8 - 10

§ Ex 8: (Testing for linearly independent) Determine whether the following set of vectors in R 3 is L. I. or L. D. Sol: 8 - 11

n Ex 9: (Testing for linearly independent) Determine whether the following set of vectors in P 2 is L. I. or L. D. Sol: S = {1+x – 2 x 2 , 2+5 x – x 2 , x+x 2} v 1 v 2 v 3 c 1 v 1+c 2 v 2+c 3 v 3 = 0 i. e. c 1(1+x – 2 x 2) + c 2(2+5 x – x 2) + c 3(x+x 2) = 0+0 x+0 x 2 c 1+2 c 2 =0 c 1+5 c 2+c 3 = 0 – 2 c 1+ c 2+c 3 = 0 This system has infinitely many solutions. (i. e. , This system has nontrivial solutions. ) S is linearly dependent. (Ex: c 1=2 , c 2= – 1 , c 3=3) 8 - 12

n Ex 10: (Testing for linearly independent) Determine whether the following set of vectors in 2× 2 matrix space is L. I. or L. D. Sol: v 1 v 2 v 3 c 1 v 1+c 2 v 2+c 3 v 3 = 0 8 - 13

2 c 1+3 c 2+ c 3 = 0 c 1 =0 2 c 2+2 c 3 = 0 c 1+ c 2 =0 c 1 = c 2 = c 3= 0 (This system has only the trivial solution. ) S is linearly independent. 8 - 14

n Thm 4. 8: (A property of linearly dependent sets) A set S = {v 1, v 2, …, vk}, k 2, is linearly independent if and only if at least one of the vectors vj in S can be written as a linear combination of the other vectors in S. Pf: ( ) c 1 v 1+c 2 v 2+…+ckvk = 0 ci 0 for some i 8 - 15

Let vi = d 1 v 1+…+di-1 vi-1+di+1 vi+1+…+dkvk = 0 c 1=d 1 , c 2=d 2 , …, ci=1 , …, ck=dk (nontrivial solution) S is linearly dependent n Corollary to Theorem 4. 8: Two vectors u and v in a vector space V are linearly dependent if and only if one is a scalar multiple of the other. 8 - 16

Keywords in Section 4. 4: n linear combination：線性組合 n spanning set：生成集合 n trivial solution：顯然解 n linear independent：線性獨立 n linear dependent：線性相依 8 - 17

Lecture 8: Vector Space (cont. ) Today n Spanning Sets and Linear Independence (Cont. ) n Basis and Dimension n Rank of a Matrix and Systems of Linear Equations n Coordinates and Change of Basis n Applications 8 - 18

4. 5 Basis and Dimension n Basis: V：a vector space Spanning Sets S ={v 1, v 2, …, vn} V Bases Linearly Independent Sets S spans V (i. e. , span(S) = V ) S is linearly independent S is called a basis for V § Notes: (1) Ø is a basis for {0} (2) the standard basis for R 3: {i, j, k} i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1) 8 - 19

n (3) the standard basis for R : {e 1, e 2, …, en} e 1=(1, 0, …, 0), e 2=(0, 1, …, 0), en=(0, 0, …, 1) Ex: R 4 {(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1)} (4) the standard basis for m n matrix space: { Eij | 1 i m , 1 j n } Ex: matrix space: (5) the standard basis for Pn(x): {1, x, x 2, …, xn} Ex: P 3(x) {1, x, x 2, x 3} 8 - 20

n Thm 4. 9: (Uniqueness of basis representation) If is a basis for a vector space V, then every vector in V can be written in one and only one way as a linear combination of vectors in S. Pf: 1. span(S) = V 2. S is linearly independent span(S) = V Let v = c 1 v 1+c 2 v 2+…+cnvn v = b 1 v 1+b 2 v 2+…+bnvn 0 = (c 1–b 1)v 1+(c 2 – b 2)v 2+…+(cn – bn)vn c 1= b 1 , c 2= b 2 , …, cn= bn 8 - 21 (i. e. , uniqueness)

n Thm 4. 10: (Bases and linear dependence) If is a basis for a vector space V, then every set containing more than n vectors in V is linearly dependent. Pf: Let S 1 = {u 1, u 2, …, um} , m > n ui V 8 - 22

Let k 1 u 1+k 2 u 2+…+kmum= 0 d 1 v 1+d 2 v 2+…+dmvm= 0(di = ci 1 k 1+ci 2 k 2+…+cimkm) di=0 i i. e. Thm 1. 1: If the homogeneous system has fewer equations than variables, then it must have infinitely many solution. m > n k 1 u 1+k 2 u 2+…+kmum = 0 has nontrivial solution S 1 is linearly dependent 8 - 23

n Thm 4. 11: (Number of vectors in a basis) If a vector space V has one basis with n vectors, then every basis for V has n vectors. (All bases for a finite-dimensional vector space has the same number of vectors. ) Pf: S ={v 1, v 2, …, vn} S'={u 1, u 2, …, un} two bases for a vector space 8 - 24

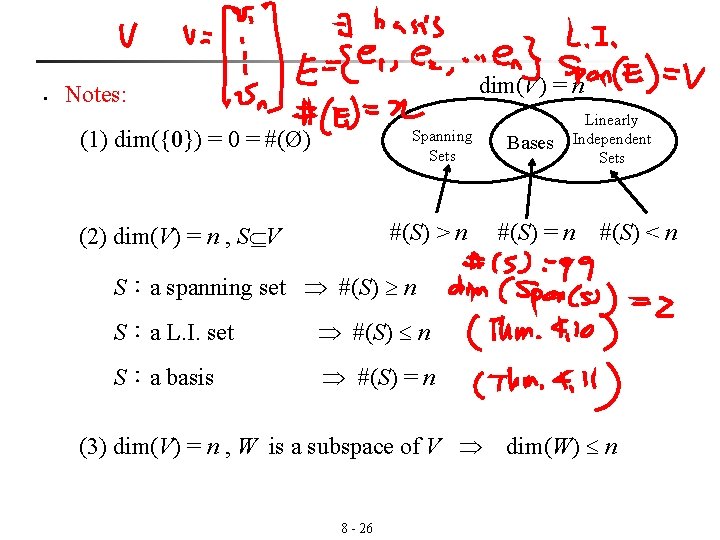
n n Finite dimensional: A vector space V is called finite dimensional, if it has a basis consisting of a finite number of elements. Infinite dimensional: If a vector space V is not finite dimensional, then it is called infinite dimensional. n Dimension: The dimension of a finite dimensional vector space V is defined to be the number of vectors in a basis for V. V: a vector space dim(V) = #(S) S：a basis for V (the number of vectors in S) 8 - 25

§ dim(V) = n Notes: (1) dim({0}) = 0 = #(Ø) Spanning Sets #(S) > n (2) dim(V) = n , S V Bases Linearly Independent Sets #(S) = n #(S) < n S：a spanning set #(S) n S：a L. I. set #(S) n S：a basis #(S) = n (3) dim(V) = n , W is a subspace of V 8 - 26 dim(W) n

n Ex: (1) Vector space Rn basis {e 1 , e 2 , , en} (2) Vector space Mm n dim(Rn) = n basis {Eij | 1 i m , 1 j n} dim(Mm n)=mn (3) Vector space Pn(x) basis {1, x, x 2, , xn} dim(Pn(x)) = n+1 (4) Vector space P(x) basis {1, x, x 2, } dim(P(x)) = 8 - 27

n Ex 9: (Finding the dimension of a subspace) (a) W={(d, c–d, c): c and d are real numbers} (b) W={(2 b, b, 0): b is a real number} Sol: (Note: Find a set of L. I. vectors that spans the subspace) (a) (d, c– d, c) = c(0, 1, 1) + d(1, – 1, 0) S = {(0, 1, 1) , (1, – 1, 0)} (S is L. I. and S spans W) S is a basis for W dim(W) = #(S) = 2 (b) S = {(2, 1, 0)} spans W and S is L. I. S is a basis for W dim(W) = #(S) = 1 8 - 28

§ Ex 11: (Finding the dimension of a subspace) Let W be the subspace of all symmetric matrices in M 2 2. What is the dimension of W? Sol: spans W and S is L. I. S is a basis for W dim(W) = #(S) = 3 8 - 29

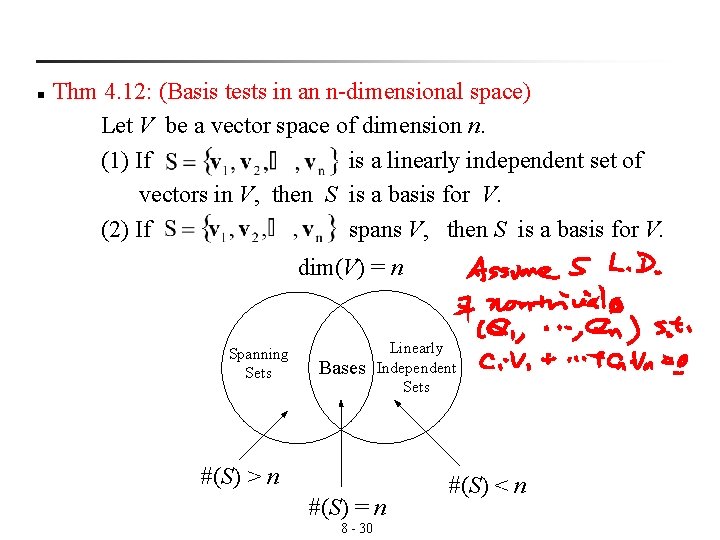
n Thm 4. 12: (Basis tests in an n-dimensional space) Let V be a vector space of dimension n. (1) If is a linearly independent set of vectors in V, then S is a basis for V. (2) If spans V, then S is a basis for V. dim(V) = n Spanning Sets Bases Linearly Independent Sets #(S) > n #(S) = n 8 - 30 #(S) < n

Keywords in Section 4. 5: n basis：基底 n dimension：維度 n finite dimension：有限維度 n infinite dimension：無限維度 8 - 31

Lecture 8: Vector Space (cont. ) Today n Spanning Sets and Linear Independence (Cont. ) n Basis and Dimension n Rank of a Matrix and Systems of Linear Equations n Coordinates and Change of Basis n Applications 8 - 32

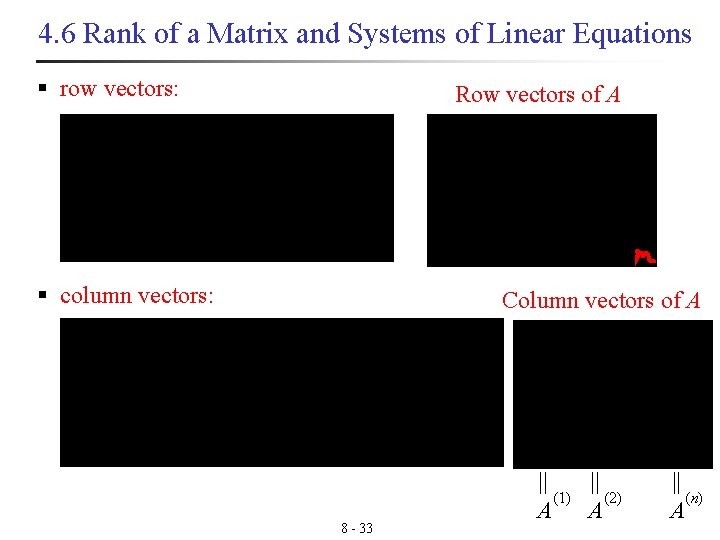
4. 6 Rank of a Matrix and Systems of Linear Equations § row vectors: Row vectors of A § column vectors: Column vectors of A 8 - 33 || || (1) (2) A A || (n) A

Let A be an m×n matrix. § Row space: The row space of A is the subspace of Rn spanned by the row vectors of A. § Column space: The column space of A is the subspace of Rm spanned by the column vectors of A. n Null space: The null space of A is the set of all solutions of Ax=0 and it is a subspace of Rn. 8 - 34

n Thm 4. 13: (Row-equivalent matrices have the same row space) If an m n matrix A is row equivalent to an m n matrix B, then the row space of A is equal to the row space of B. n Notes: (1) The row space of a matrix is not changed by elementary row operations. RS(r(A)) = RS(A) r: elementary row operations (2) Elementary row operations can change the column space. 8 - 35

n Thm 4. 14: (Basis for the row space of a matrix) If a matrix A is row equivalent to a matrix B in row-echelon form, then the nonzero row vectors of B form a basis for the row space of A. 8 - 36

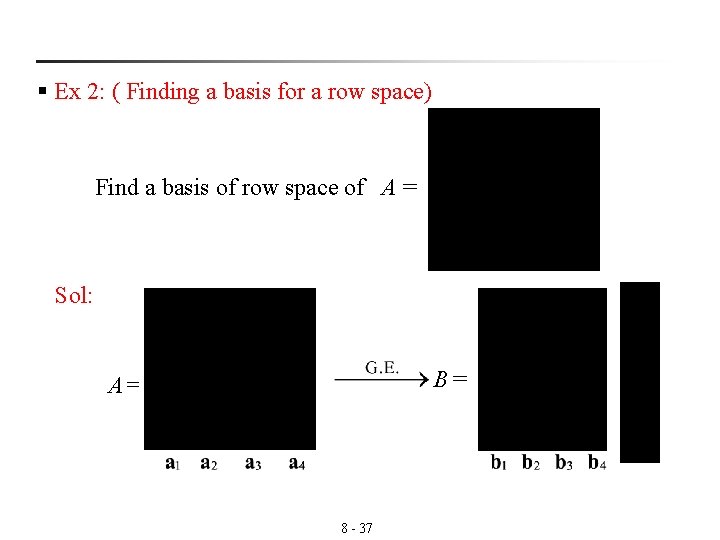
§ Ex 2: ( Finding a basis for a row space) Find a basis of row space of A = Sol: B= A= 8 - 37

n a basis for RS(A) = {the nonzero row vectors of B} (Thm 4. 14) = {w 1, w 2, w 3} = {(1, 3, 1, 3) , (0, 1, 1, 0) , (0, 0, 0, 1)} Notes: 8 - 38

n Ex 3: (Finding a basis for a subspace) Find a basis for the subspace of R 3 spanned by Sol: A= G. E. a basis for span({v 1, v 2, v 3}) = a basis for RS(A) = {the nonzero row vectors of B} = {w 1, w 2} = {(1, – 2, – 5) , (0, 1, 3)} 8 - 39 (Thm 4. 14)

n Ex 4: (Finding a basis for the column space of a matrix) Find a basis for the column space of the matrix A given in Ex 2. Sol. 1: 8 - 40

CS(A)=RS(AT) a basis for CS(A) = a basis for RS(AT) = {the nonzero vectors of B} = {w 1, w 2, w 3} (a basis for the column space of A) § Note: This basis is not a subset of {c 1, c 2, c 3, c 4}. 8 - 41

n Sol. 2: Leading 1 => {v 1, v 2, v 4} is a basis for CS(B) {c 1, c 2, c 4} is a basis for CS(A) § Notes: (1) This basis is a subset of {c 1, c 2, c 3, c 4}. (2) v 3 = – 2 v 1+ v 2, thus c 3 = – 2 c 1+ c 2. 8 - 42

n Thm 4. 16: (Solutions of a homogeneous system) If A is an m n matrix, then the set of all solutions of the homogeneous system of linear equations Ax = 0 is a subspace Pf: of Rn called the nullspace of A. § Notes: The nullspace of A is also called the solution space of the homogeneous system Ax = 0. 8 - 43

§ Ex 6: (Finding the solution space of a homogeneous system) Find the nullspace of the matrix A. Sol: The nullspace of A is the solution space of Ax = 0. x 1 = – 2 s – 3 t, x 2 = s, x 3 = –t, x 4 = t 8 - 44

n Thm 4. 15: (Row and column space have equal dimensions) If A is an m n matrix, then the row space and the column space of A have the same dimension. dim(RS(A)) = dim(CS(A)) § Rank: The dimension of the row (or column) space of a matrix A is called the rank of A. rank(A) = dim(RS(A)) = dim(CS(A)) 8 - 45

§ Nullity: The dimension of the nullspace of A is called the nullity of A. nullity(A) = dim(NS(A)) § Notes: rank(AT) = rank(A) Pf: rank(AT) = dim(RS(AT)) = dim(CS(A)) = rank(A) 8 - 46

n Thm 4. 17: (Dimension of the solution space) If A is an m n matrix of rank r, then the dimension of the solution space of Ax = 0 is n – r. That is n = rank(A) + nullity(A) n Notes: (1) rank(A): The number of leading variables in the solution of Ax=0. (The number of nonzero rows in the row-echelon form of A) (2) nullity (A): The number of free variables in the solution of Ax = 0. 8 - 47

n Notes: If A is an m n matrix and rank(A) = r, then Fundamental Space Dimension RS(A)=CS(AT) r CS(A)=RS(AT) r NS(A) n–r NS(AT) m–r 8 - 48

n Ex 7: (Rank and nullity of a matrix) Let the column vectors of the matrix A be denoted by a 1, a 2, a 3, a 4, and a 5. a 1 a 2 (a) Find the rank and nullity of A. a 3 a 4 a 5 (b) Find a subset of the column vectors of A that forms a basis for the column space of A. (c) If possible, write third column of A as a linear combination of the first two columns. 8 - 49

Sol: Let B be the reduced row-echelon form of A. a 1 a 2 a 3 a 4 (a) rank(A) = 3 a 5 b 1 b 2 b 3 b 4 b 5 (the number of nonzero rows in B) 8 - 50

(b) Leading 1 (c) 8 - 51

§ Thm 4. 18: (Solutions of a nonhomogeneous linear system) If xp is a particular solution of the nonhomogeneous system Ax = b, then every solution of this system can be written in the form x = xp + xh , wher xh is a solution of the corresponding homogeneous system Ax = 0. Pf: Let x be any solution of Ax = b. is a solution of Ax = 0 8 - 52

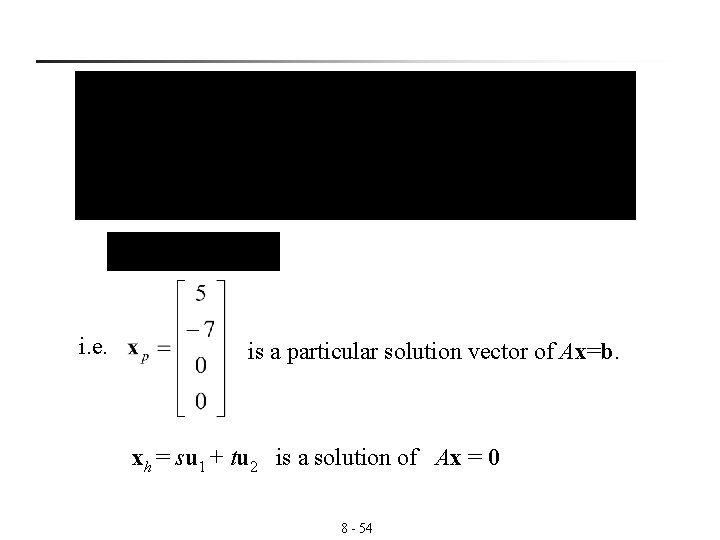
n Ex 8: (Finding the solution set of a nonhomogeneous system) Find the set of all solution vectors of the system of linear equations. Sol: s 8 - 53 t

i. e. is a particular solution vector of Ax=b. xh = su 1 + tu 2 is a solution of Ax = 0 8 - 54

n Thm 4. 19: (Solution of a system of linear equations) The system of linear equations Ax = b is consistent if and only if b is in the column space of A. Pf: Let be the coefficient matrix, the column matrix of unknowns, and the right-hand side, respectively, of the system Ax = b. 8 - 55

Then Hence, Ax = b is consistent if and only if b is a linear combination of the columns of A. That is, the system is consistent if and only if b is in the subspace of Rm spanned by the columns of A. 8 - 56

§ Notes: If rank([A|b])=rank(A) Then the system Ax=b is consistent. n Ex 9: (Consistency of a system of linear equations) Sol: 8 - 57

c 1 c 2 c 3 b w 1 w 2 w 3 v (b is in the column space of A) The system of linear equations is consistent. § Check: 8 - 58

n Summary of equivalent conditions for square matrices: If A is an n×n matrix, then the following conditions are equivalent. (1) A is invertible (2) Ax = b has a unique solution for any n× 1 matrix b. (3) Ax = 0 has only the trivial solution (4) A is row-equivalent to In (5) (6) rank(A) = n (7) The n row vectors of A are linearly independent. (8) The n column vectors of A are linearly independent. 8 - 59

Keywords in Section 4. 6: n row space : 列空間 n column space : 行空間 n null space: 零空間 n solution space : 解空間 n rank: 秩 n nullity : 核次數 8 - 60

Lecture 8: Vector Space (cont. ) Today n Spanning Sets and Linear Independence (Cont. ) n Basis and Dimension n Rank of a Matrix and Systems of Linear Equations n Coordinates and Change of Basis n Applications 8 - 61

Lecture 8: Vector Space Today n Spanning Sets and Linear Independence (Cont. ) n Basis and Dimension n Rank of a Matrix and Systems of Linear Equations Reading Assignment: Secs 4. 4 - 4. 6 Next Time n Midterm Exam (14: 20 – 16: 00, 11/16) n Scope: Chapters 1 -4. 6 n Homework-like problems: 80% n In-class Q&A type and advanced problems: 20% 8 - 62