Chapter 2 Matrices provide an orderly way of







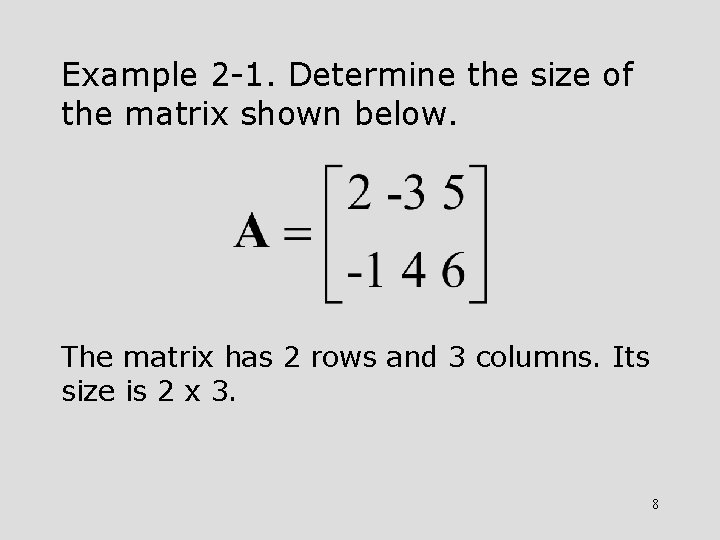

















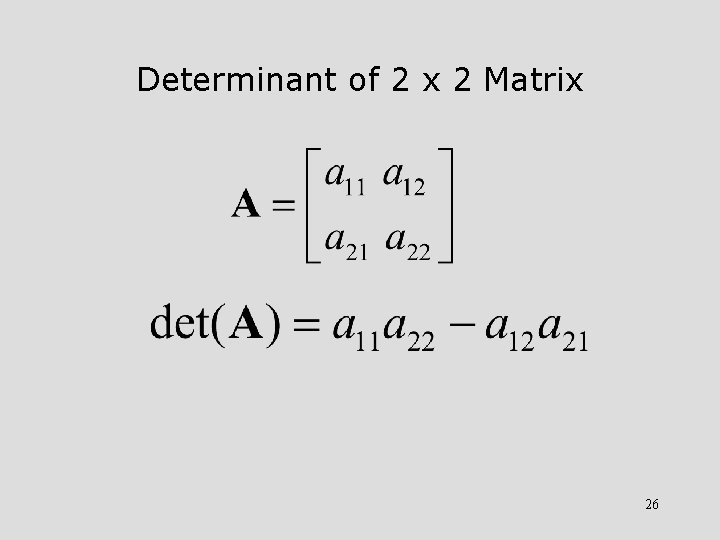














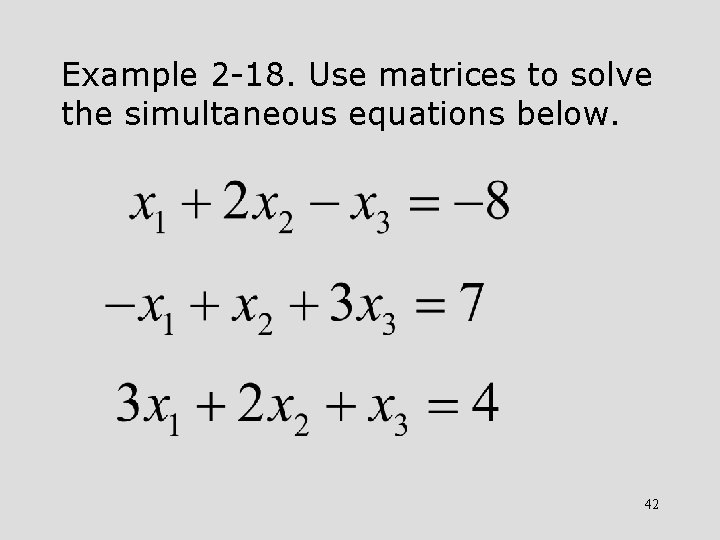


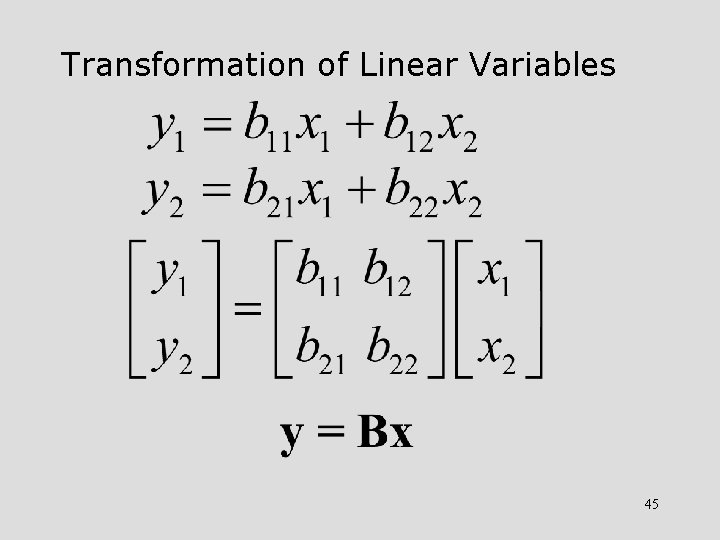

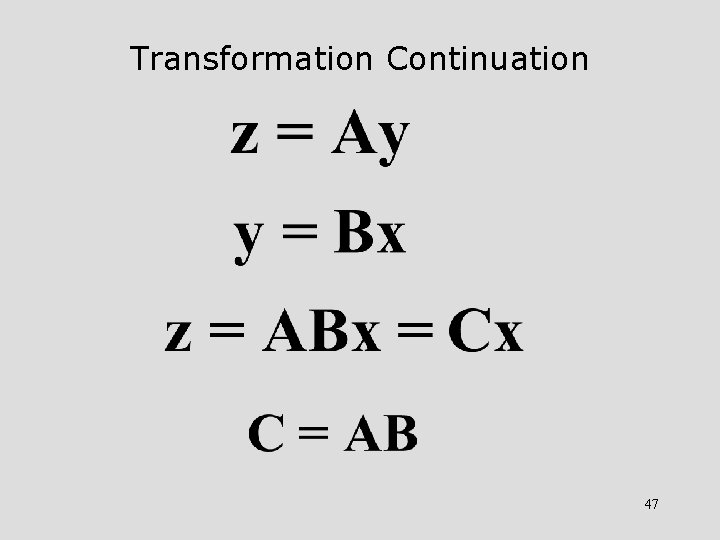



- Slides: 50

Chapter 2 Matrices provide an orderly way of arranging values or functions to enhance the analysis of systems in a systematic manner. Their use is very important in simplifying large arrays of equations and in determining their solutions. In particular, computer algorithms for manipulating large arrays are simplified greatly by matrix notation and operations. 1

A particular reason for introducing matrices at this point is that MATLAB is heavily matrix oriented. One does not have to be an expert in matrix theory to utilize the powerful features of MATLAB, but it is very helpful to understand some of the terminology and manipulations. This chapter will deal with those basic elements of matrix theory that can be used for that purpose. The term linear algebra is often used to represent the general theory of matrices and the associated algebraic operations. 2

General Form of a Matrix of Size m x n with m Rows and n Columns 3

Square Matrix If m = n, the matrix is said to be square. In this case, the matrix could be designated as an m x m matrix. 4

Vectors A matrix having only one row is called a row matrix. A matrix having only one column is called a column matrix. A matrix of either form is called a vector. The row matrix is called a row vector and the column matrix is called a column vector. 5

Scalars A 1 x 1 matrix is called a scalar and is the form of most variables considered in simple algebraic forms. 6

Transpose The transpose of a matrix A is denoted as A’ and is obtained by interchanging the rows and columns. Thus, if A has a size of m x n, A’ will have a size of n x m. If the transpose operation is applied twice, the original matrix is restored. 7
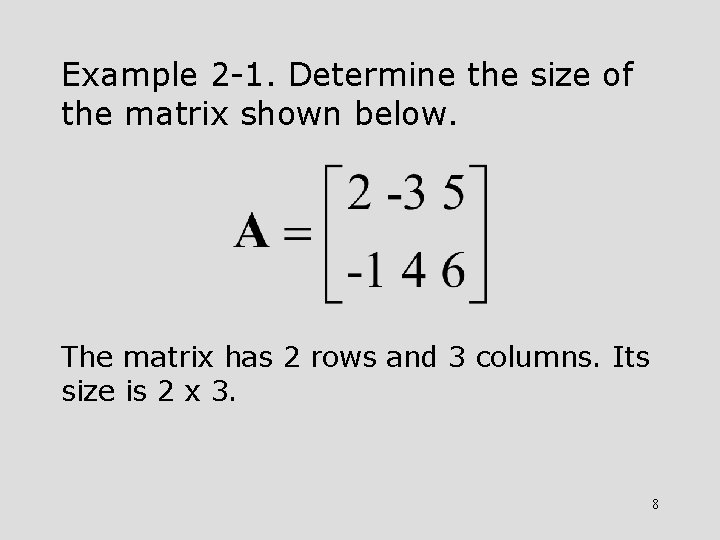
Example 2 -1. Determine the size of the matrix shown below. The matrix has 2 rows and 3 columns. Its size is 2 x 3. 8

Example 2 -2. Determine the size of the matrix shown below. The matrix has 3 rows and 2 columns. Its size is 3 x 2. 9

Example 2 -3. Determine the size of the matrix shown below. The matrix has 3 rows and 3 columns. Its size is 3 x 3. It is a square matrix. 10

Example 2 -4. Express the integer values of time from 0 to 5 s as a row vector. The size of the vector is 1 x 6. 11

Example 2 -5. Express the variables x 1, x 2, and x 3 as a column vector. 12

Example 2 -6. Determine the transpose of the matrix A below. 13

Addition and Subtraction of Matrices can be added together or subtracted from each other if and only if they are of the same size. Corresponding elements are added or subtracted. 14

Multiplication of Two Matrices Two matrices can be multiplied together only if the number of columns of the first matrix is equal to the number of rows of the second matrix. This means that 15

Multiplication of Two Matrices (Continuation) The number of rows in the product matrix is equal to the number of rows in the first matrix and the number of columns in the product matrix is equal to the number of columns in the second matrix. 16

Multiplication of Two Matrices (Continuation) An element in the product matrix is obtained by summing successive products of elements in the row of the first with elements of the column of the second. 17

Division of Matrices ? There is no such thing as division of matrices. However, matrix inversion can be viewed in some sense as a procedure similar to division. This process will be considered later. 18

Example 2 -7. Determine C = A + B for the matrices shown below. 19

Example 2 -8. Determine D = A - B for the matrices shown below. 20

Example 2 -9. For the matrices of Examples 2 -1 and 2 -2, determine possible orders of multiplication. 21

Example 2 -10. For the matrices of Examples 2 -1 and 2 -2, determine C=AB. 22

Example 2 -10. Continuation. 23

Example 2 -11. For the matrices of Examples 2 -1 and 2 -2, determine D=BA. 24

Determinants The determinant of a matrix A can be determined only for a square matrix. It is a scalar value. Various representations are shown as follows: 25
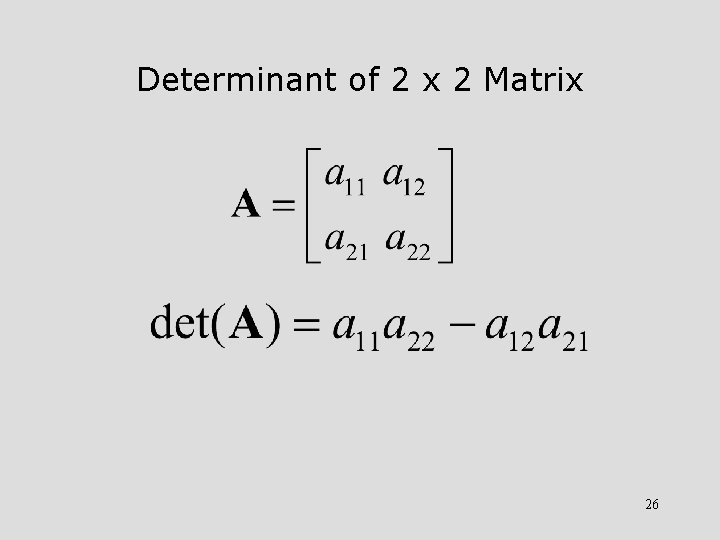
Determinant of 2 x 2 Matrix 26

Determinants of Higher-Order For determinants of matrices of higher order than 2 x 2, the process can become tedious. There are many “tricks”, but some are useful only when the matrix has simple numbers. The text provides a procedure based on minors and cofactors, but since the ultimate goal is to use MATLAB, that procedure will not be covered on these slides. Instead, formulas for the 3 x 3 case will be provided. 27

Determinant of 3 x 3 Matrix 28

Singular Matrix If det(A)=0, the matrix is said to be singular. If the matrix represents the coefficients of a set of simultaneous equations, it means that the equations are not independent of each other and cannot be solved uniquely. 29

Example 2 -13. Determine the determinant of the matrix shown below. 30

Examples 2 -13, 2 -14, and 2 -15 These 3 examples involve computations concerning the minors and cofactors of a 3 x 3 matrix and will not covered in this presentation. The results that follow these computations will be considered in a later example. 31

Identity Matrix 32

Inverse Matrix The inverse of a matrix A is denoted by A-1 and is defined by the equation that follows. 33

Inverse of a 2 x 2 Matrix 34

Example 2 -16. Determine the inverse of the matrix A below. 35

Example 2 -17. The inverse of A below is developed in the text. 36

Simultaneous Linear Equations 37

Matrix Form of Simultaneous Linear Equations 38

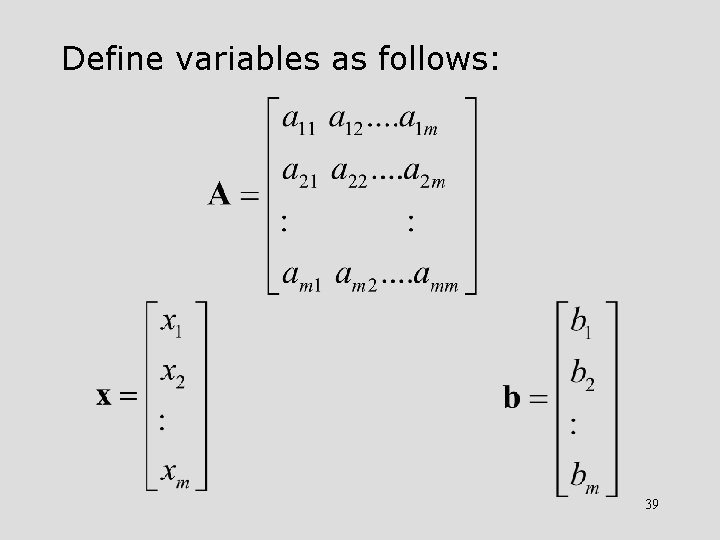
Define variables as follows: 39

Matrix Solution Development 40

The general form and the final solution follow. 41
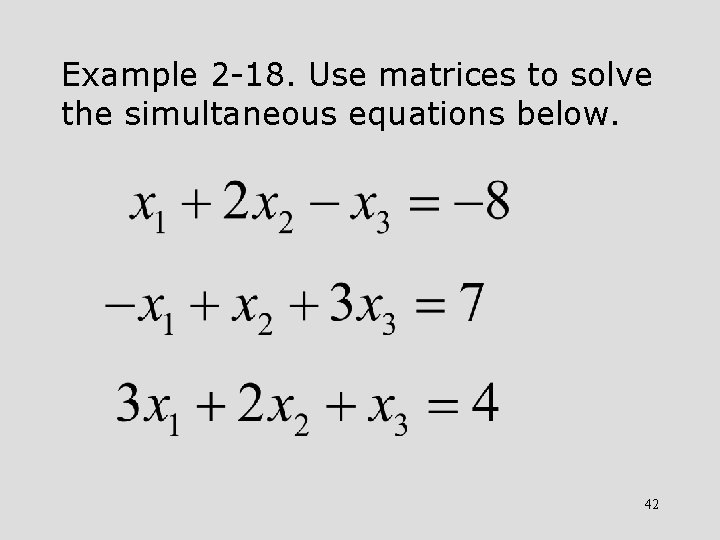
Example 2 -18. Use matrices to solve the simultaneous equations below. 42

Example 2 -18. Continuation. 43

Example 2 -18. Continuation. 44
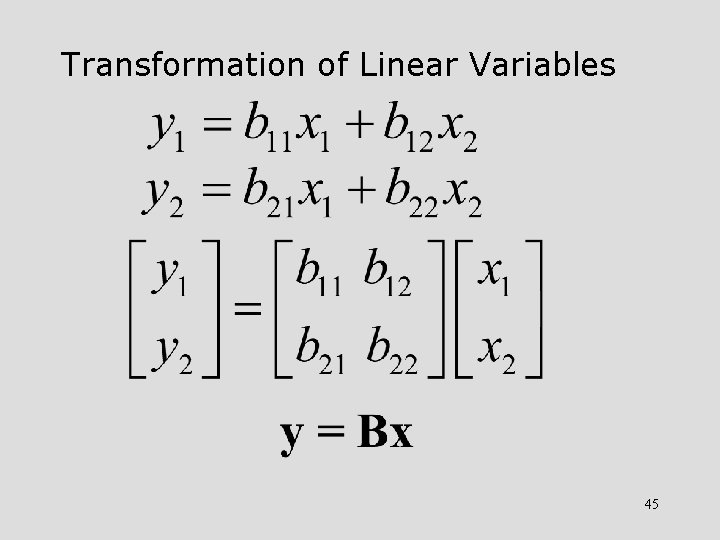
Transformation of Linear Variables 45

Transformation Continuation 46
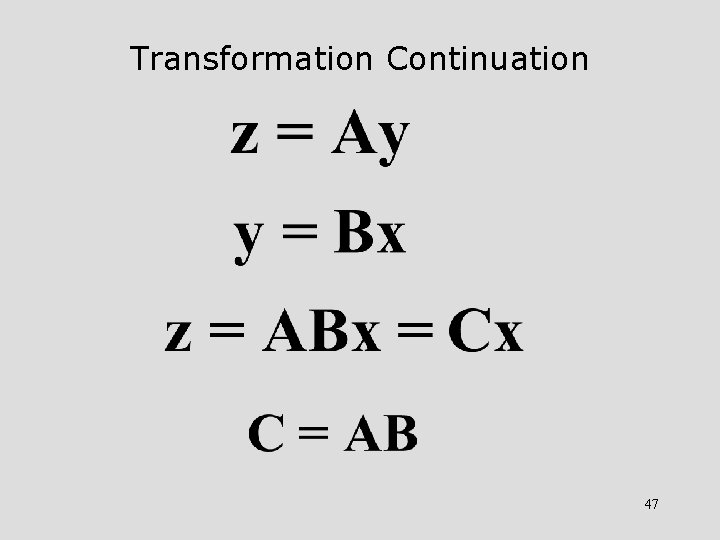
Transformation Continuation 47

Example 2 -19. For the system of equations provided below, determine the z values in terms of the x values. 48

Example 2 -19. Continuation. 49

Example 2 -19. Continuation. 50
 Chapter 4 matrices answers
Chapter 4 matrices answers Homogeneous system of linear equations examples
Homogeneous system of linear equations examples Relative frequency two way table
Relative frequency two way table Two way anova
Two way anova Threaded binary tree advantages and disadvantages
Threaded binary tree advantages and disadvantages Perbedaan anova one way dan two way
Perbedaan anova one way dan two way Anova test
Anova test One way anova vs two way anova
One way anova vs two way anova Analisis two way anova
Analisis two way anova Conventional software engineering
Conventional software engineering This way that way forwards backwards over the irish sea
This way that way forwards backwards over the irish sea Talk this way
Talk this way Orderly development meaning
Orderly development meaning Is a consistent, orderly or pleasing arrangement of parts.
Is a consistent, orderly or pleasing arrangement of parts. Particle theory of matter
Particle theory of matter Give an example of an orderly visual search pattern
Give an example of an orderly visual search pattern The tokugawa shoguns created an orderly society by
The tokugawa shoguns created an orderly society by Ipde
Ipde 4-6 second range
4-6 second range You should practice your orderly visual search pattern
You should practice your orderly visual search pattern It advocates orderly approach to software engineering
It advocates orderly approach to software engineering To compromise space means to
To compromise space means to Principles of developmentally appropriate practice
Principles of developmentally appropriate practice An orderly presentation crossword clue
An orderly presentation crossword clue Sere in ecological succession
Sere in ecological succession Chapter 5 managing risk with the ipde process
Chapter 5 managing risk with the ipde process Ipde examples
Ipde examples Communities biomes and ecosystems
Communities biomes and ecosystems Chapter 14 principles of hair design worksheet
Chapter 14 principles of hair design worksheet Hair design
Hair design An orderly visual search pattern
An orderly visual search pattern Orderly (50%)chaotic (50%)
Orderly (50%)chaotic (50%) Nature is orderly
Nature is orderly Matrici progresive raven standard raspunsuri
Matrici progresive raven standard raspunsuri Cuando una matriz es idempotente
Cuando una matriz es idempotente Division de matrices 3x3
Division de matrices 3x3 Can matrices be divided
Can matrices be divided Linearly independent vectors
Linearly independent vectors Wj-iv sentence writing fluency scoring
Wj-iv sentence writing fluency scoring Perinatal matrices grof
Perinatal matrices grof Propiedades matriz inversa
Propiedades matriz inversa Ejemplos de igualdad de matrices
Ejemplos de igualdad de matrices Simultaneous equations matrix
Simultaneous equations matrix Window matrix dental
Window matrix dental Matrix operations
Matrix operations What is i in matrix
What is i in matrix Matriz epistemologica
Matriz epistemologica Vector space properties
Vector space properties Matrices for dummies
Matrices for dummies 3 by 3 matrix
3 by 3 matrix Matrice fcb
Matrice fcb