Chapter 2 Matrices 2 1 Operations with Matrices




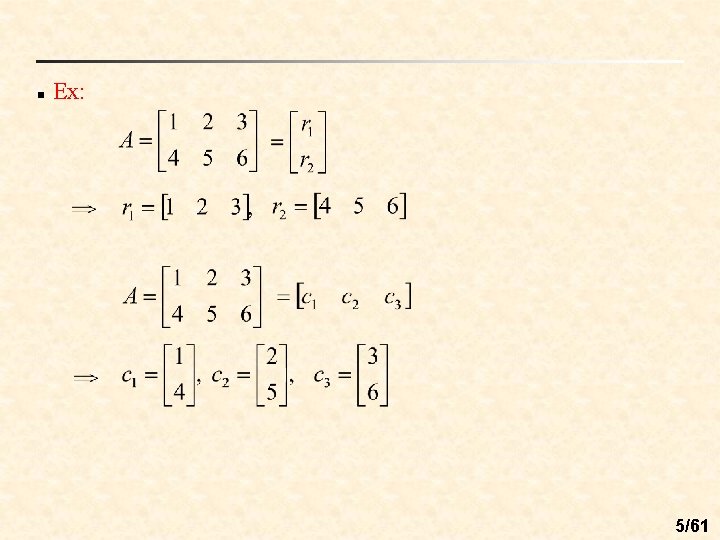
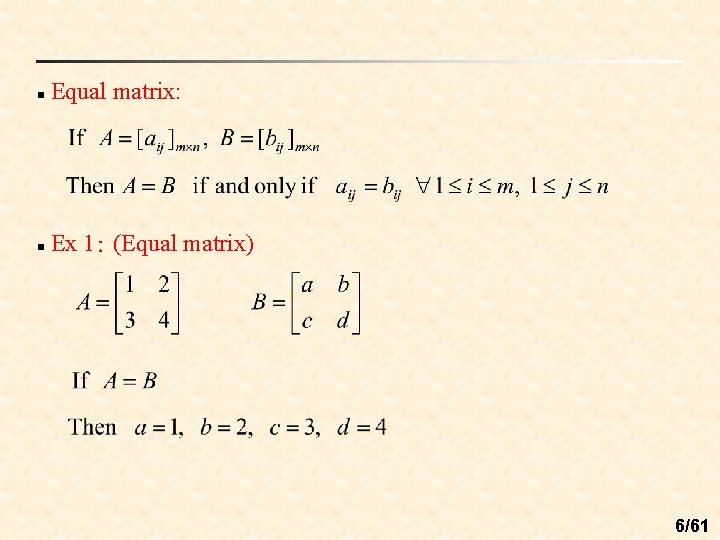


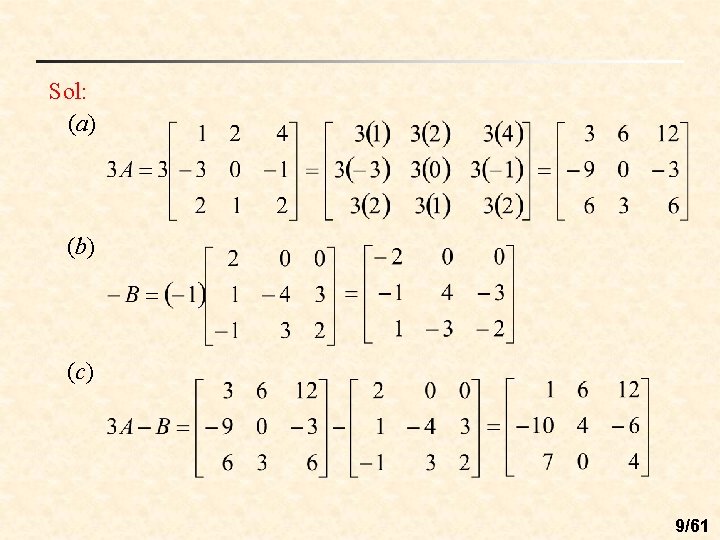













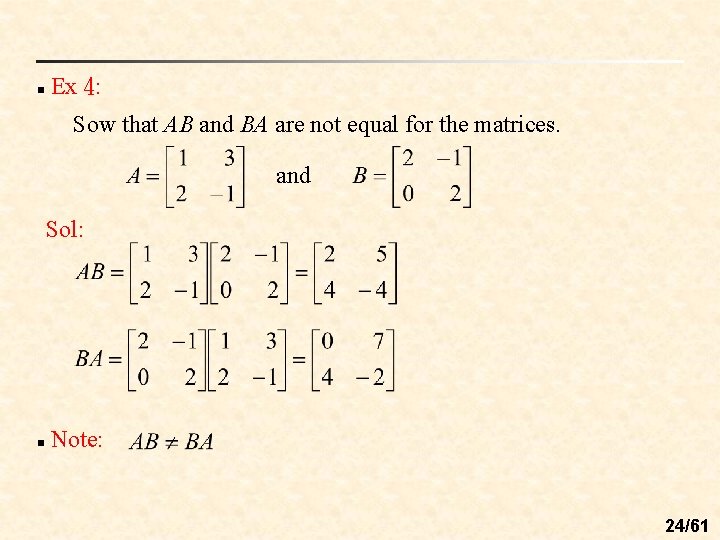






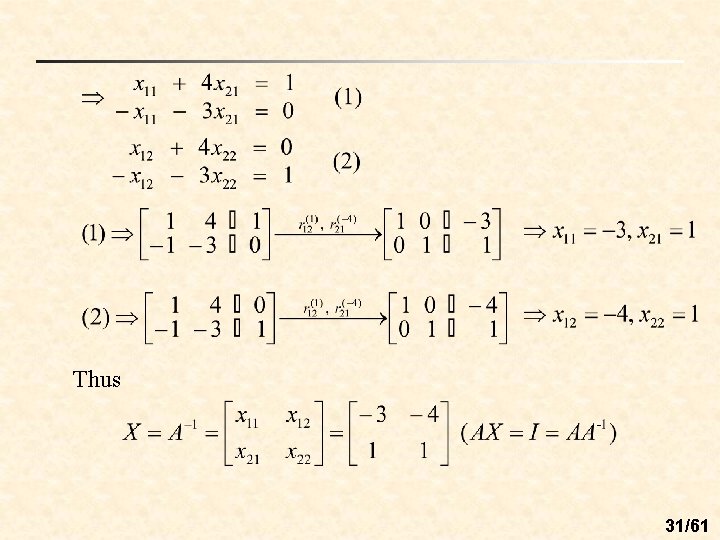













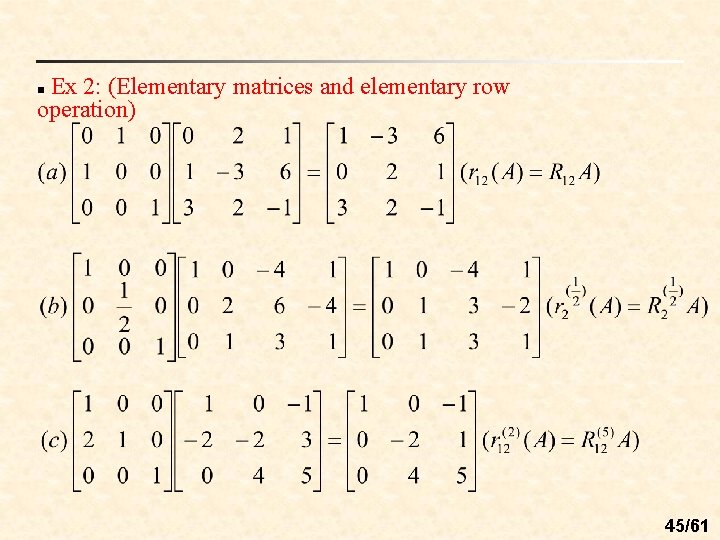







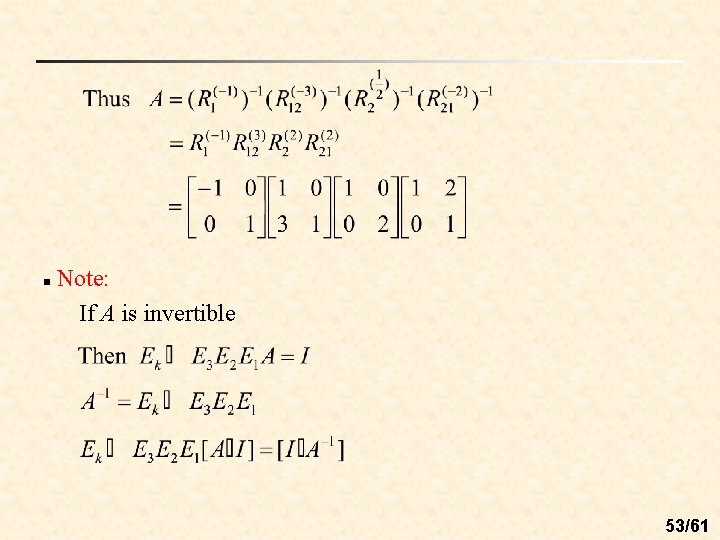



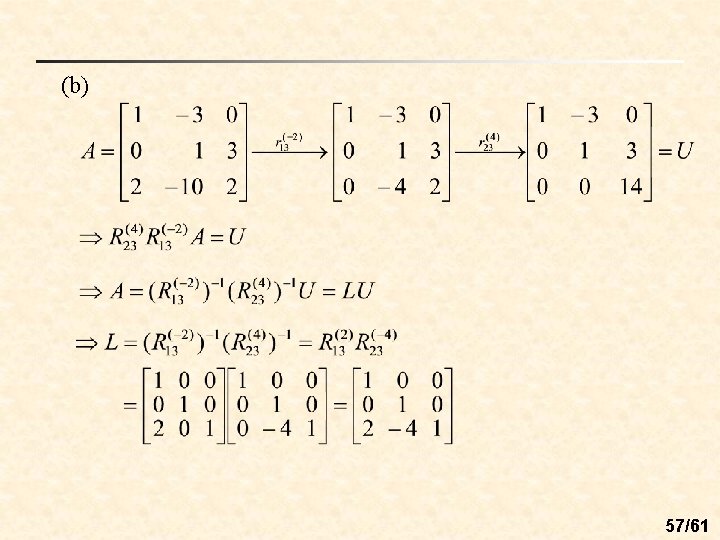




- Slides: 61

Chapter 2 Matrices 2. 1 Operations with Matrices 2. 2 Properties of Matrix Operations 2. 3 The Inverse of a Matrix 2. 4 Elementary Matrices

2. 1 Operations with Matrices n Matrix: (i, j)-th entry: row: m column: n size: m×n 2/61

n i-th row vector row matrix n j-th column vector column matrix n Square matrix: m=n 3/61

n Diagonal matrix: n Trace: 4/61
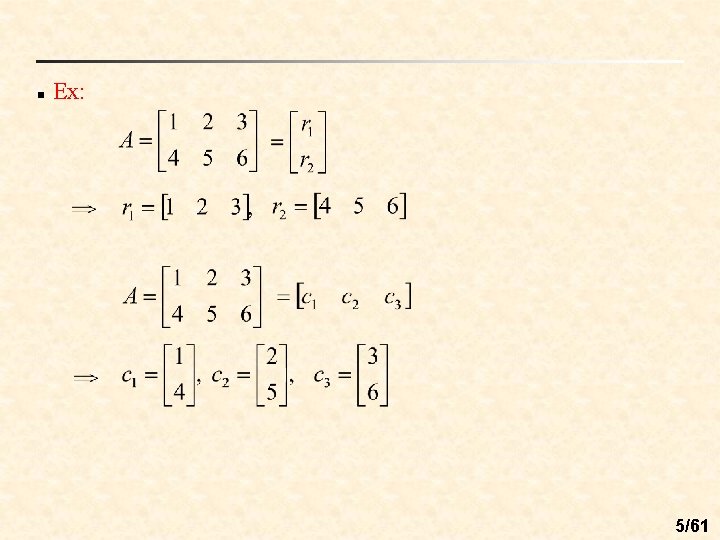
n Ex: 5/61
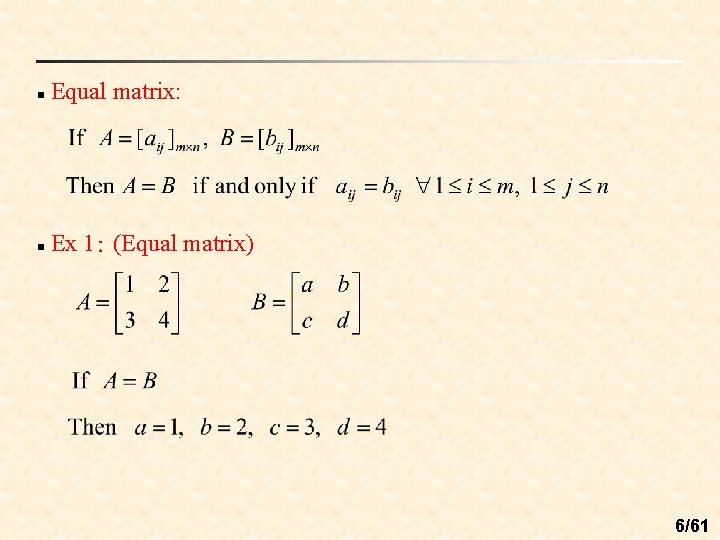
n Equal matrix: n Ex 1: (Equal matrix) 6/61

n n Matrix addition: Ex 2: (Matrix addition) 7/61

n Scalar multiplication: n Matrix subtraction: n Ex 3: (Scalar multiplication and matrix subtraction) Find (a) 3 A, (b) –B, (c) 3 A – B 8/61
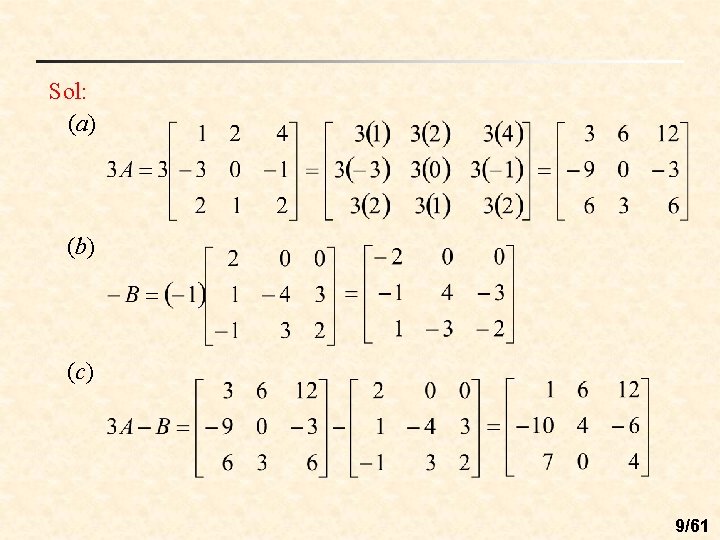
Sol: (a) (b) (c) 9/61

n Matrix multiplication: Size of AB where n Notes: (1) A+B = B+A, (2) 10/61

n Ex 4: (Find AB) Sol: 11/61

n Matrix form of a system of linear equations: x = = = A b 12/61

n Partitioned matrices: submatrix 13/61

Keywords in Section 2. 1: n row vector: ﻣﺘﺠﻪ ﺻﻔﻲ n column vector: ( )ﻣﺘﺠﻪ ﻋﻤﻮﺩﻱ Might imply orthogonal vector! n diagonal matrix: ﻣﺼﻔﻮﻓﺔ ﻗﻄﺮﻳﺔ n trace: ﺍﺛﺮ n equality of matrices: ﺗﻌﺎﺩﻝ ﺍﻟﻤﺼﻔﻮﻓﺎﺕ n matrix addition: ﺟﻤﻊ ﺍﻟﻤﺼﻔﻮﻓﺎﺕ n scalar multiplication: ﺿﺮﺏ ﺑﻌﺪﺩ ﺛﺎﺑﺖ n matrix multiplication: ﺿﺮﺏ ﺍﻟﻤﺼﻔﻮﻓﺎﺕ n partitioned matrix: ﻣﺼﻔﻮﻓﺔ ﻣﺠﺰﺋﺔ 14/61

2. 2 Properties of Matrix Operations n Three basic matrix operators: (1) matrix addition (2) scalar multiplication (3) matrix multiplication n Zero matrix: n Identity matrix of order n: 15/61

n Properties of matrix addition and scalar multiplication: Then (1) A+B = B + A (2) A + ( B + C ) = ( A + B ) + C (3) ( cd ) A = c ( d. A ) (4) 1 A = A (5) c( A+B ) = c. A + c. B (6) ( c+d ) A = c. A + d. A 16/61

n Properties of zero matrices: n Notes: (1) 0 m×n: the additive identity for the set of all m×n matrices (2) –A: the additive inverse of A 17/61

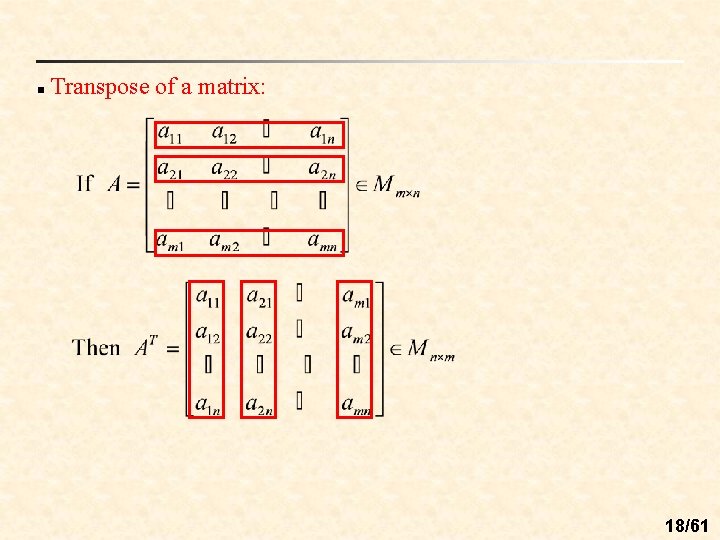
n Transpose of a matrix: 18/61

n Ex 8: (Find the transpose of the following matrix) (a) (b) (c ) Sol: (a) (b) (c ) 19/61

n Properties of transposes: 20/61

n Symmetric matrix: A square matrix A is symmetric if A = AT n Skew-symmetric matrix: A square matrix A is skew-symmetric if AT = –A n Ex: is symmetric, find a, b, c? Sol: 21/61

n Ex: is a skew-symmetric, find a, b, c? Sol: n Note: is symmetric Pf: 22/61

n n Real number: ab = ba (Commutative law for multiplication) Matrix: Three situations: (Sizes are not the same) (Sizes are the same, but matrices are not equal) 23/61
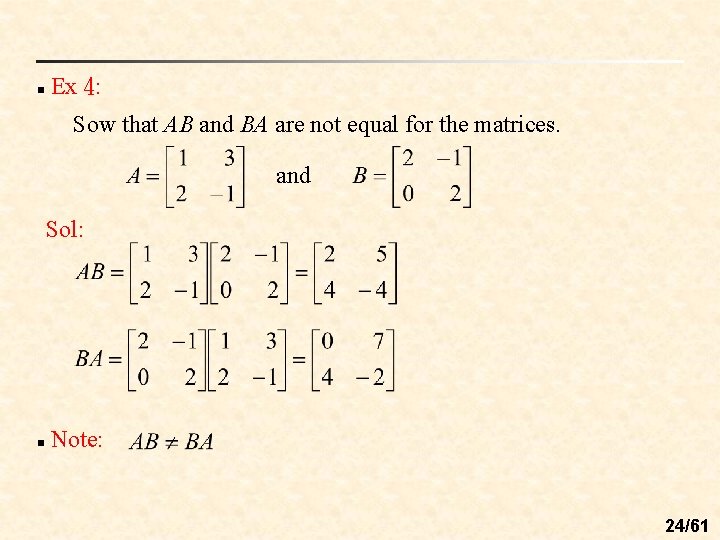
n Ex 4: Sow that AB and BA are not equal for the matrices. and Sol: n Note: 24/61

n Real number: (Cancellation law) n Matrix: (1) If C is invertible, then A = B (Cancellation is not valid) 25/61

n Ex 5: (An example in which cancellation is not valid) Show that AC=BC Sol: So But 26/61


2. 3 The Inverse of a Matrix n Inverse matrix: Consider Then (1) A is invertible (or nonsingular) (2) B is the inverse of A n Note: A matrix that does not have an inverse is called noninvertible (or singular). 28/61

n Thm 2. 7: (The inverse of a matrix is unique) If B and C are both inverses of the matrix A, then B = C. Pf: Consequently, the inverse of a matrix is unique. Note s: (1) The inverse of A is denoted by n 29/61

Find the inverse of a matrix by Gauss-Jordan Elimination: n n Ex 2: (Find the inverse of the matrix) Sol: 30/61
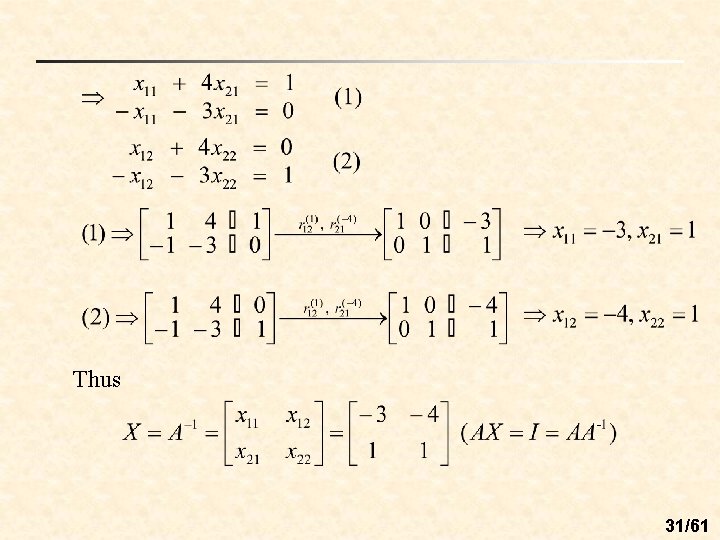
Thus 31/61

n Note: If A can’t be row reduced to I, then A is singular. 32/61

n Ex 3: (Find the inverse of the following matrix) Sol: 33/61

So the matrix A is invertible, and its inverse is n Check: 34/61

n Power of a square matrix: 35/61

n Thm 2. 8: (Properties of inverse matrices) If A is an invertible matrix, k is a positive integer, and c is a scalar not equal to zero, then 36/61

n Thm 2. 9: (The inverse of a product) If A and B are invertible matrices of size n, then AB is invertible and Pf: n Note: 37/61

n Thm 2. 10 (Cancellation properties) If C is an invertible matrix, then the following properties hold: (1) If AC=BC, then A=B (Right cancellation property) (2) If CA=CB, then A=B (Left cancellation property) Pf: n e: Not If C is not invertible, then cancellation is not valid. 38/61

n Thm 2. 11: (Systems of equations with unique solutions) If A is an invertible matrix, then the system of linear equations Ax = b has a unique solution given by Pf: ( A is nonsingular) (Left cancellation property) This solution is unique. 39/61

n Note: For square systems (those having the same number of equations as variables), Theorem 2. 11 can be used to determine whether the system has a unique solution. n Note: (A is an invertible matrix) 40/61

Keywords in Section 2. 3: n inverse matrix: ﻣﺼﻔﻮﻓﺔ ﻋﻜﺴﻴﺔ n invertible: ﻗﺎﺑﻠﺔ ﻟﻠﻌﻜﺲ n nonsingular: ﻏﻴﺮ ﻣﻨﻔﺮﺩ n singular: ﻣﻨﻔﺮﺩ n power: ﻗﻮﺓ 41/61

2. 4 Elementary Matrices n Row elementary matrix: An n n matrix is called an elementary matrix if it can be obtained from the identity matrix In by a single elementary operation. n Three row elementary matrices: Interchange two rows. Multiply a row by a nonzero constant. Add a multiple of a row to another row. n Note: Only do a single elementary row operation. 42/61

n Ex 1: (Elementary matrices and nonelementary matrices) 43/61

n Thm 2. 12: (Representing elementary row operations) Let E be the elementary matrix obtained by performing an elementary row operation on Im. If that same elementary row operation is performed on an m n matrix A, then the resulting matrix is given by the product EA. n Notes: 44/61
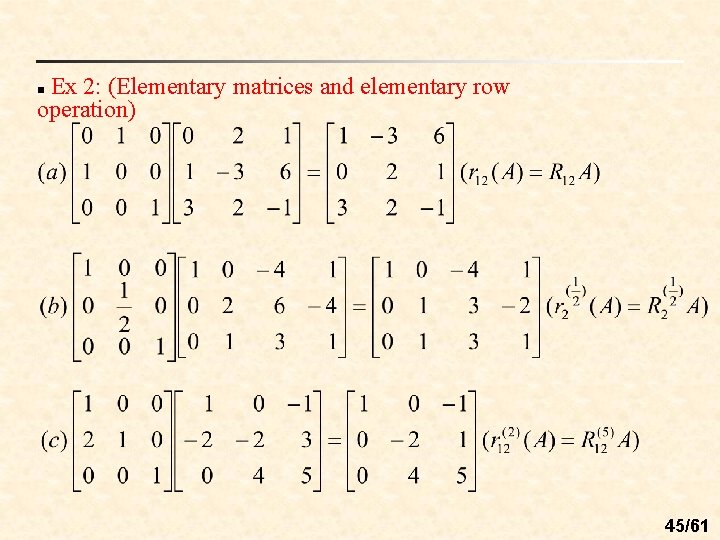
Ex 2: (Elementary matrices and elementary row operation) n 45/61

n Ex 3: (Using elementary matrices) Find a sequence of elementary matrices that can be used to write the matrix A in row-echelon form. Sol: 46/61

row-echelon form 47/61

n Row-equivalent: Matrix B is row-equivalent to A if there exists a finite number of elementary matrices such that 48/61

n Thm 2. 13: (Elementary matrices are invertible) If E is an elementary matrix, then exists and is an elementary matrix. n Notes: 49/61

n Ex: Elementary Matrix Inverse Matrix (Elementary Matrix) 50/61

n Thm 2. 14: (A property of invertible matrices) A square matrix A is invertible if and only if it can be written as the product of elementary matrices. Pf: (1) Assume that A is the product of elementary matrices. (a) Every elementary matrix is invertible. (b) The product of invertible matrices is invertible. Thus A is invertible. (2) If A is invertible, has only the trivial solution. (Thm. 2. 11) Thus A can be written as the product of elementary matrices. 51/61

n Ex 4: Find a sequence of elementary matrices whose product is Sol: 52/61
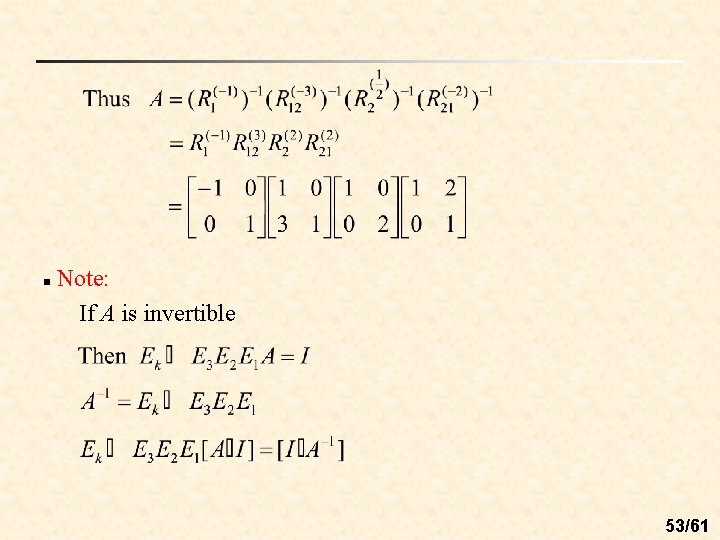
n Note: If A is invertible 53/61

n Thm 2. 15: (Equivalent conditions) If A is an n n matrix, then the following statements are equivalent. (1) A is invertible. (2) Ax = b has a unique solution for every n 1 column matrix b. (3) Ax = 0 has only the trivial solution. (4) A is row-equivalent to In. (5) A can be written as the product of elementary matrices. 54/61

n LU-factorization: If the n n matrix A can be written as the product of a lower triangular matrix L and an upper triangular matrix U, then A=LU is an LU-factorization of A n L is a lower triangular matrix U is an upper triangular matrix Note: If a square matrix A can be row reduced to an upper triangular matrix U using only the row operation of adding a multiple of one row to another row below it, then it is easy to find an LUfactorization of A. 55/61

n Ex 5: (LU-factorization) Sol: (a) 56/61
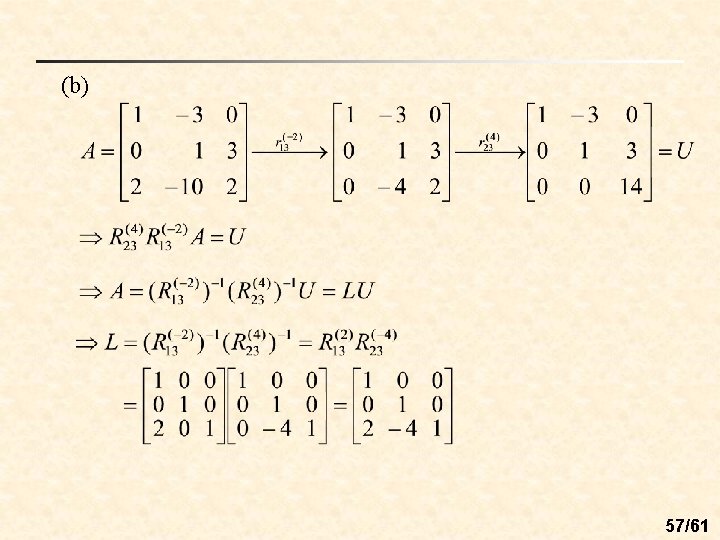
(b) 57/61

n n Solving Ax=b with an LU-factorization of A Two steps: (1) Write y = Ux and solve Ly = b for y (2) Solve Ux = y for x 58/61

n Ex 7: (Solving a linear system using LU-factorization) Sol: 59/61

So Thus, the solution is 60/61

Keywords in Section 2. 4: n row elementary matrix: ﻣﺼﻔﻮﻓﺔ ﺻﻔﻴﺔ ﺃﻮﻟﻴﺔ n row equivalent: ﺗﻜﺎﻓﺆ ﺻﻔﻲ n lower triangular matrix: ﻣﺼﻔﻮﻓﺔ ﻣﺜﻠﺜﻴﺔ ﺳﻔﻠﻰ n upper triangular matrix: ﻣﺼﻔﻮﻓﺔ ﻣﺜﻠﺜﻴﺔ ﻋﻠﻴﺎ n LU-factorization: LU – ﺗﺤﻠﻴﻞ 61/61