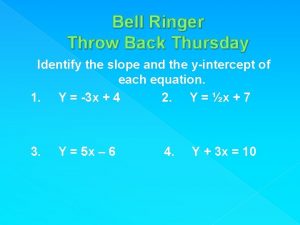Bell Ringer You throw a football horizontally and

Bell Ringer You throw a football horizontally, and drop a football from the same height and at the same time. Which will hit the ground first? PLEASE DO NOT DISCUSS YOUR ANSWER WITH THOSE AROUND YOU!!!!!

Bell Ringer A bullet is dropped at the same time a second bullet is shot horizontally. Which will collide with the ground first? Why does this occur?

Projectile Motion

Vectors Vector: A quantity with direction Represented by arrows Length = Size of quantity Points in the direction of vector quantity

Adding Vectors Tail of Vector Head of Vector Resultant Vector: The sum of two or more vectors When adding vectors, always arrange them HEAD to TAIL Resultant: From the tail of the 1 st vector to the head of the last

Adding Vectors Graphical Method: Slide vectors anywhere on the page as long as they maintain their length and direction The order in which the vectors are combined does not matter
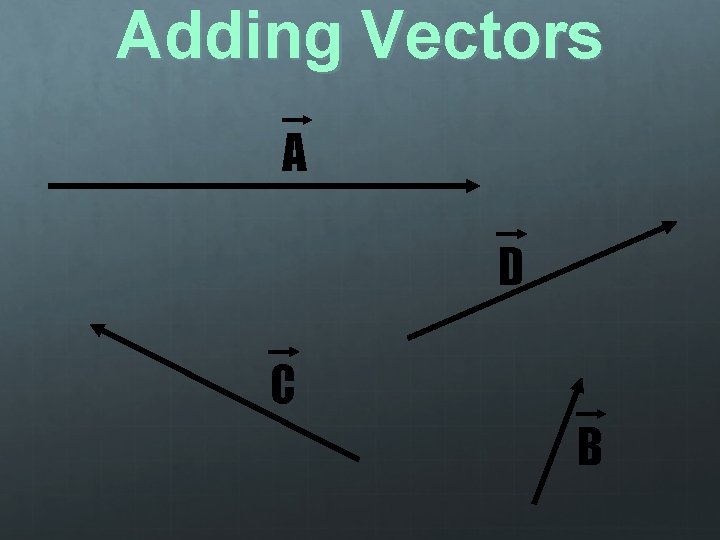
Adding Vectors A D C B
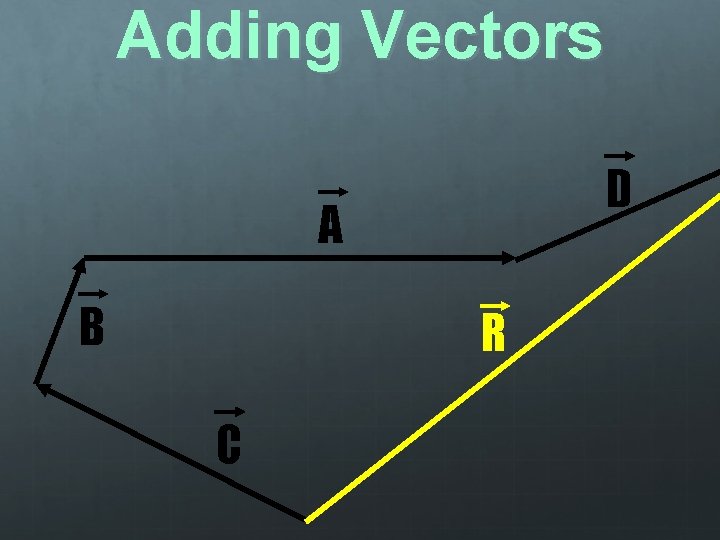
Adding Vectors D A B R C
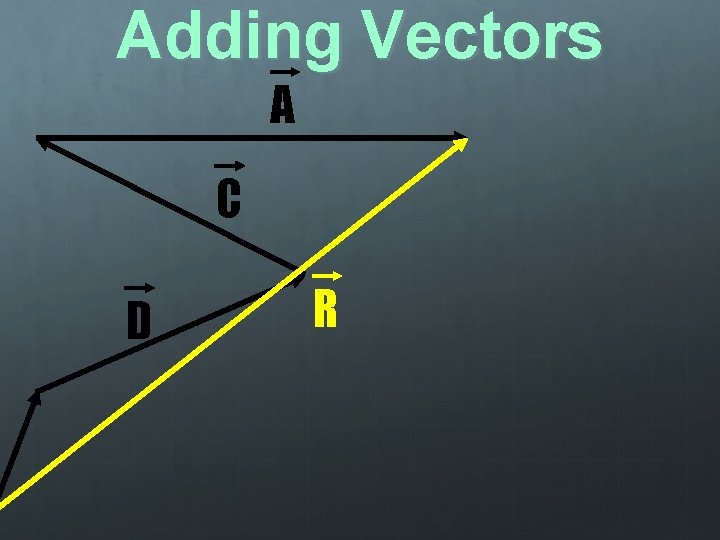
Adding Vectors A C D R

Bell Ringer What is the horizontal component of a 15 m vector, with a vertical component of 9 m?

Wind and Plane in Same Direction 35 mph 350 mph The plane’s velocity and the wind velocity can be represented by vector arrows

Wind and Plane in Same Direction 35 mph 350 mph The overall velocity of the plane, is the sum of the wind velocity and the original velocity of the plane

Wind and Plane in Same Direction 35 mph 350 mph Align the vectors head to tail and draw the resultant vector from the tail of the first vector to the head of the second vector

Wind and Plane in Same Direction v = 385 mph 350 mph Therefore: v = vwind + vplane v = 385 mph
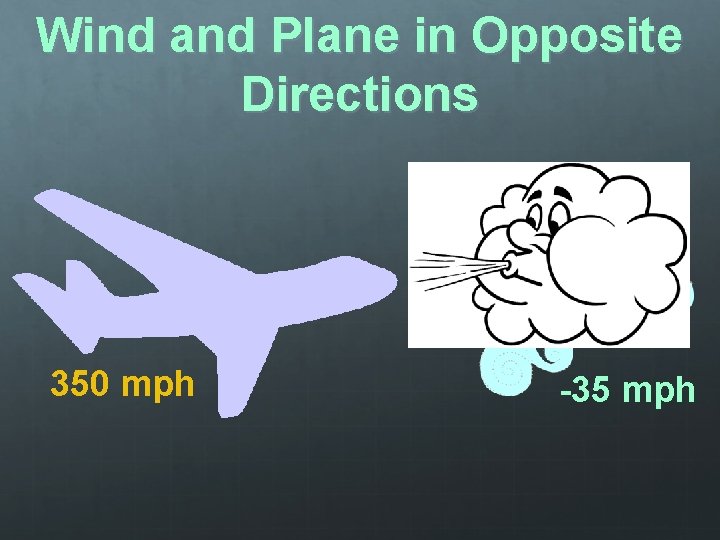
Wind and Plane in Opposite Directions 350 mph -35 mph
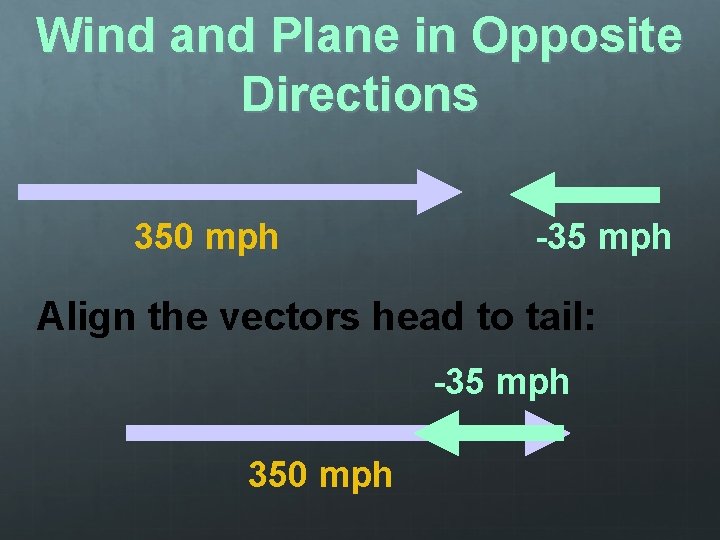
Wind and Plane in Opposite Directions 350 mph -35 mph Align the vectors head to tail: -35 mph 350 mph

Wind and Plane in Opposite Directions v -35 mph 350 mph Therefore: v = vwind + vplane v =mph) 315 mph v = (-35 + 350 mph
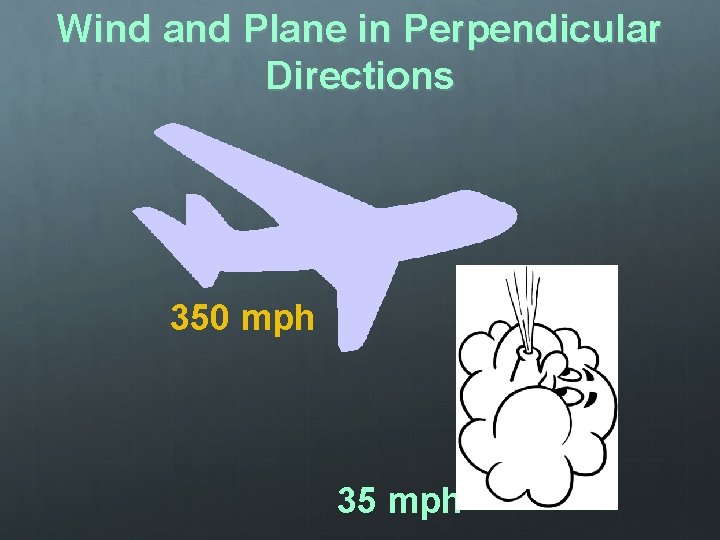
Wind and Plane in Perpendicular Directions 350 mph 35 mph
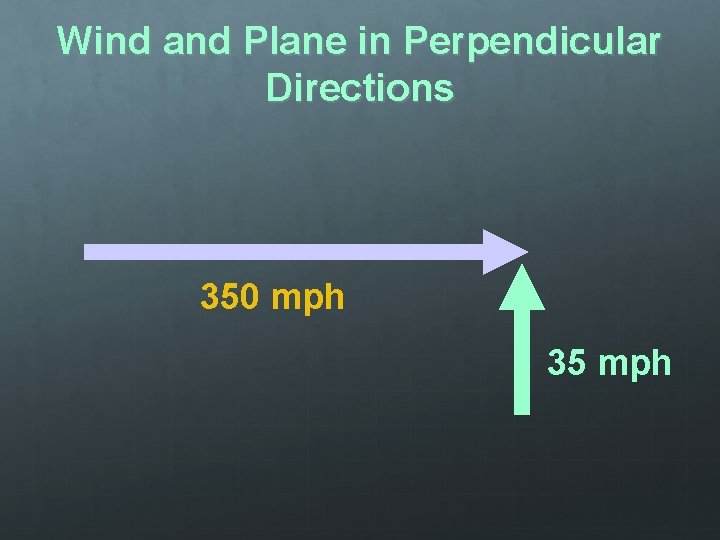
Wind and Plane in Perpendicular Directions 350 mph 35 mph
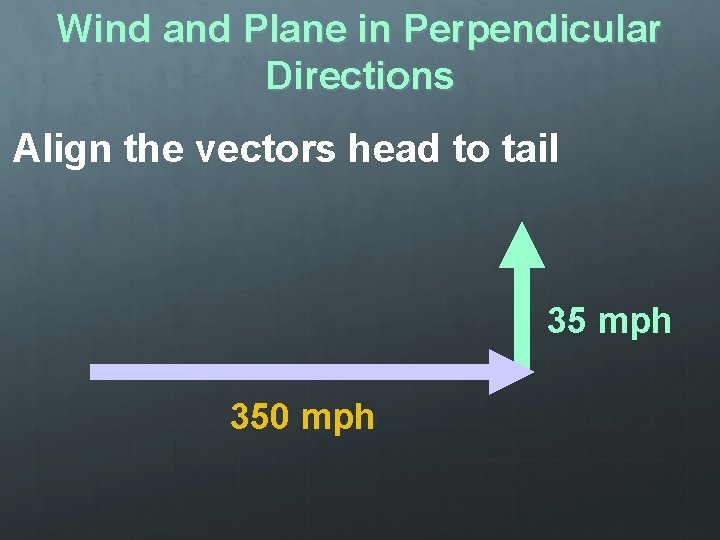
Wind and Plane in Perpendicular Directions Align the vectors head to tail 35 mph 350 mph
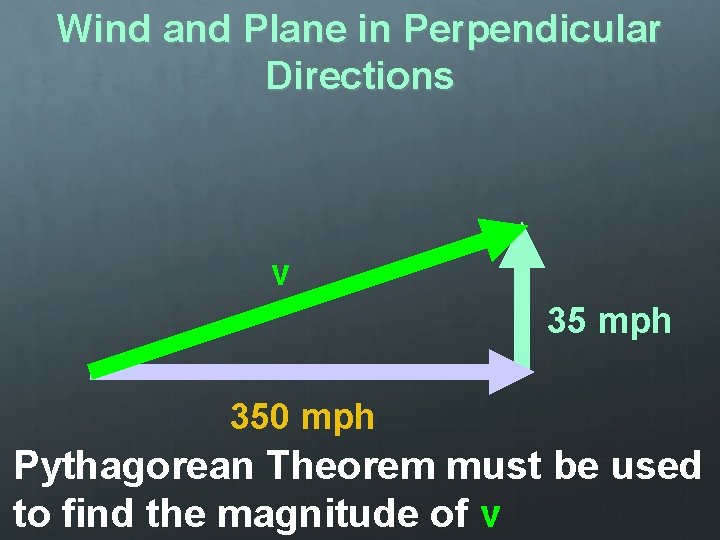
Wind and Plane in Perpendicular Directions v 35 mph 350 mph Pythagorean Theorem must be used to find the magnitude of v
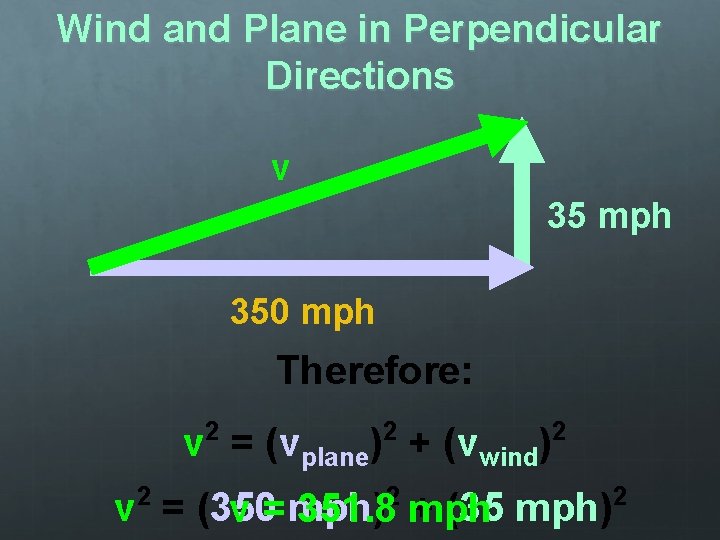
Wind and Plane in Perpendicular Directions v 35 mph 350 mph Therefore: 2 2 v = (vplane) + (vwind) 2 2 2 v = (350 + (35 mph) v = mph) 351. 8 mph 2

Vector Components Part of a vector x-component: Determines how far horizontally the vector is tilted y-component: Determines how far vertically the vector is tilted
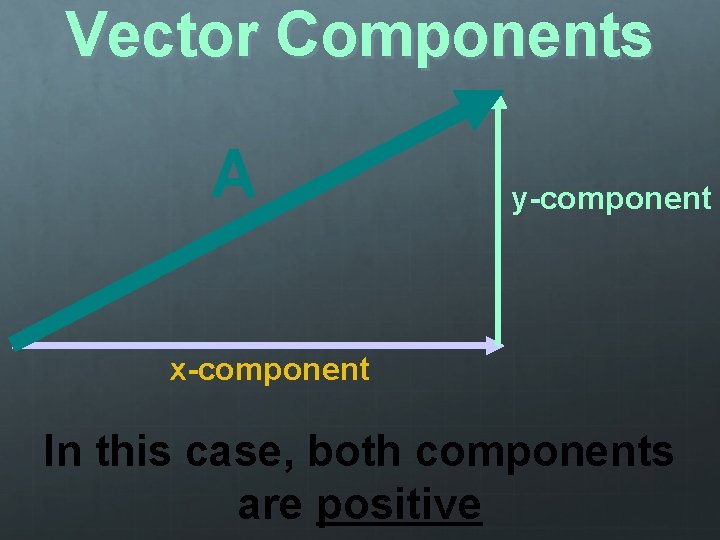
Vector Components A y-component x-component In this case, both components are positive

Bell Ringer While flying due east at 120 km/h, an airplane is also carried northward at 45 km/h by the wind blowing due north. What is the plane’s resultant velocity?

Projectile Motion Acts only under the influence of gravity and air resistance AND… Follows a curved, 2 -D path

x-component Neglecting air resistance, the horizontal velocity of a projectile remains constant

y-component The vertical component of the velocity of a projectile changes due to gravity The object accelerates downward The y-component acts the same as an object in freefall

Projectile Motion

Projectile Motion The horizontal component of a projectile is entirely independent from the vertical component of motion Changing one does not affect the other

Projectile Motion The equations of 1 -D motion still apply (dx = vxt and dy = ½ayt 2) NEVER mix x- and y-components in the same equation DON’T MIX Time is the only scalar quantity in these equations ONLY time can be used to tie x- and y-components together

Projectile Motion A ball rolls off a level table with a speed of 2. 2 m/s. The table is 1. 2 meters high. How far away from the base of the table does the ball land?

Practice Problem A soccer ball is kicked horizontally off a 22. 0 -meter high hill and lands a distance of 35. 0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball.

Bell Ringer A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.
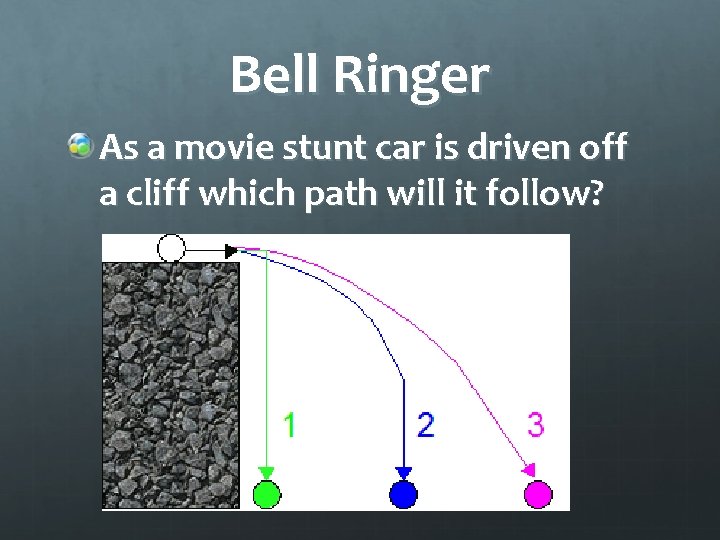
Bell Ringer As a movie stunt car is driven off a cliff which path will it follow?

Practice Problem Do this in your notebook. This is not the bell ringer A beach ball, moving with a speed of +1. 27 m/s, rolls off a pier and hits the water 0. 75 m from the end of the pier. How high is the pier above the water?

Bell Ringer If we were to find the initial velocity of a projectile shot from a perfectly horizontal gun, what things would we have to measure?

Bell Ringer A bullet has a speed of 350 m/sec as it leaves a rifle. If it is fired horizontally from a cliff 6. 4 m above a lake, how far does the bullet travel before striking the water?

Bell Ringer Make a hypothesis about which angle above the horizontal that will launch a projectile the farthest distance. Be sure to record this.

Bell Ringer Answer the two questions on the worksheet on your bell ringer paper. PLEASE DO NOT DISCUSS YOUR ANSWER WITH THOSE AROUND YOU!!!!!

Bell Ringer Explain how you will accomplish the following with your catapult. Put the same amount of energy into the catapult each time. The ball is released from the same point for each trial.

Projectile Motion At the top of its path, an object has no y-component to its velocity, it moves perfectly horizontally for an instant
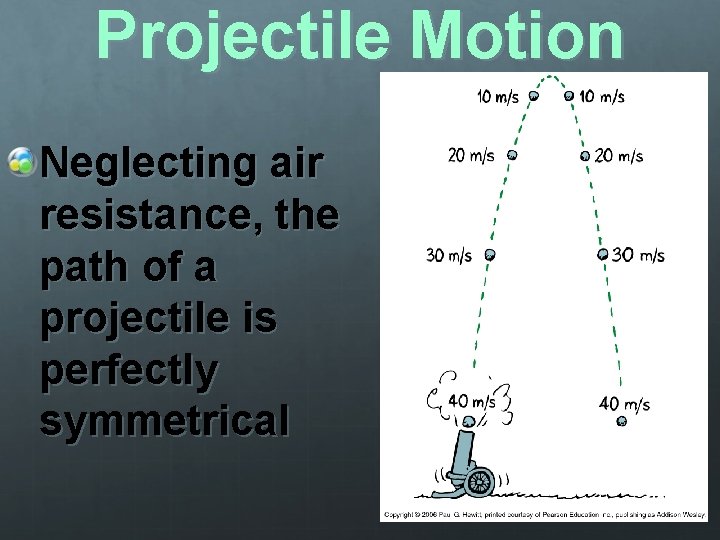
Projectile Motion Neglecting air resistance, the path of a projectile is perfectly symmetrical
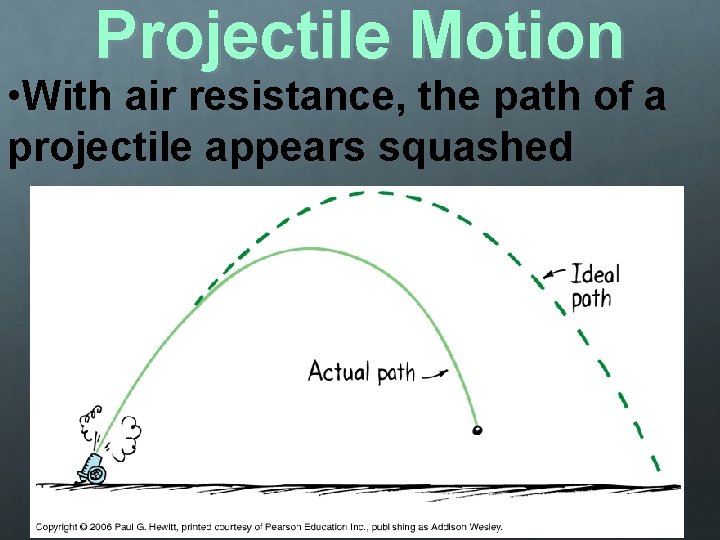
Projectile Motion • With air resistance, the path of a projectile appears squashed

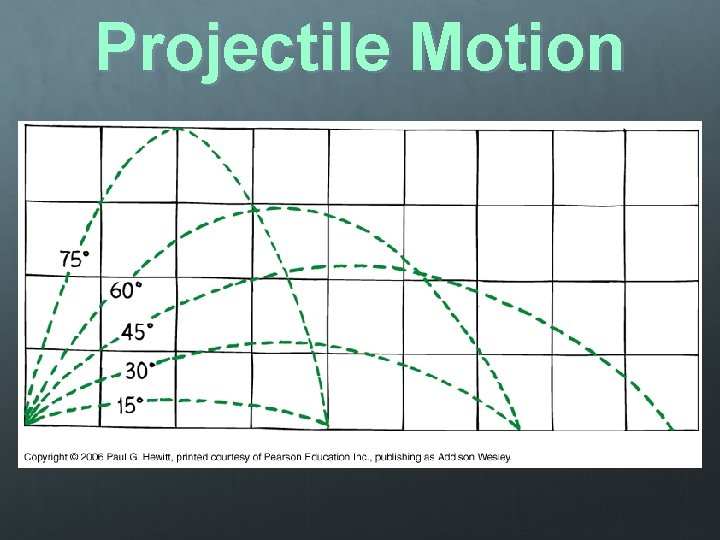
Projectile Motion Varying the angle at which a projectile is launched will change its range Range: The horizontal distance achieved by a projectile Hangtime: Total elapsed time during flight of the projectile

Projectile Motion o Launch angle >45 Height outweighs range Launch angle <45 o Range outweighs height A projectile will reach the same range when launched at angles which add to 90 o (complementary angles)

Projectile Motion Maximum range is achieved at some middle angle 45 o is its own compliment, therefore projectiles launched at this angle achieve maximum range Note: This is only true when air resistance is neglected
Projectile Motion

Satellites

Satellites
Satellites

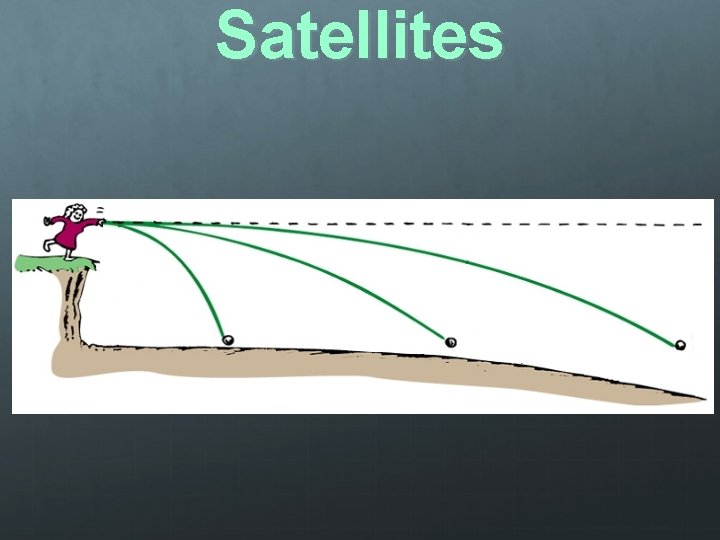
Satellites Fast moving projectiles The path of a projectile is curved, and so is the surface of the Earth If thrown at the right speed, the curvature of the trajectory of the object would match the curvature of the Earth
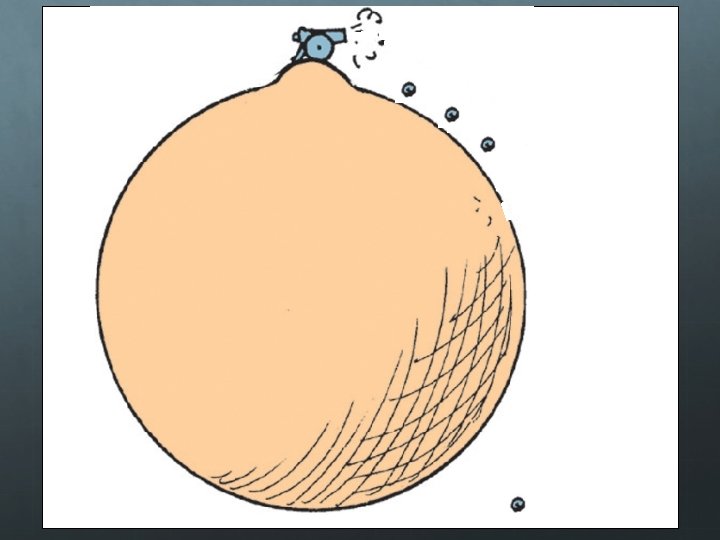

Satellites A satellite is simply a projectile traveling fast enough to fall around the Earth, rather than into it The speed needed to achieve orbit is 8 km/s or 18, 000 mph With air resistance, ordinary objects would burn up at such great speeds

Test Topics Adding Vectors Topics on the Conceptual Review Horizontal Projectile Motion Problems Projectile Motion Lab Anything else talked about after our last test Chapter 3 in your text
- Slides: 55