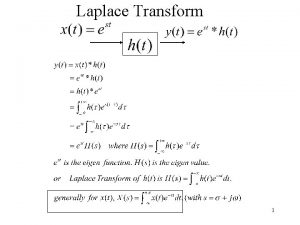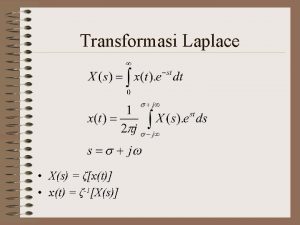Appendix I ZTransform and Laplace Transform Leonard Kleinrock

Appendix I –Z-Transform and Laplace Transform Leonard Kleinrock, Queueing Systems, Volume 1: Theory Nelson Fonseca, State University of Campinas

I. 1 Why Transforms? • They greatly simplify the calculations • They arise naturally in the formulation and the solution of systems problems • Oftentimes they are the only tools we have available for proceeding with the solution at all

f SYSTEM g • System: a mapping between the input function and the output function. The system operates on function f to produce the function g. • The f and g functions depend upon an independent time parameter t: f(t) and g(t)

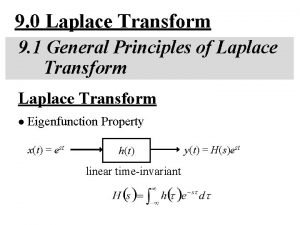
• Linear time-invariant systems: transforms do appear naturally • Linear system: where a and b are time independent variables • Time-invariant systems • Which functions of time f(t) may pass through our linear time-invariant systems with no change in form? where H is some scalar multiplier

• These functions are the “eingenfunctions” or “characteristic functions” • Answer: Complex exponential function where s is a complex variable • From the time-invariance property we must have:

• H is independent of t but may certainly be a function of s • Wish: be able to decompose the function f(t) into a sum (or integral) of complex exponentials, each of which contributes to the overall output g(t) through a computation of the form given: The overall output may be found by summing (integrating) these individual components of the output

• The Transform Method : decompose our input into sums of exponentials, compute the response to each from these exponentials, and then reconstitute the output from sums of exponentials • Linear time-invariant systems: constantcoefficient linear differential equations

Discrete-Time Systems • Discrete Time Systems: the function f is defined in some points, multiples of a unit t where n = …, -2, -1, 0, 1, 2, … • Notation: • For discrete-time systems we still have:

• Eingenfunctions • • • H how much of a given complex exponential we get out of our linear system when we insert a unit amount of that exponential at the input system (or transfer) function

• Definition: Kronecker delta function (or unit function) •

Let us make the change of variable for the sum on the right-hand side of expression, giving:

I. 2 The Z-Transform

• The disk |Z| < 1 represents a range of analyticity for F(Z) is the sum of is finite

Z-Transform properties

• Inspection method to find the sequence given the Z-Transform – Look for terms that are easily invertible

• It is necessary to divide the denominator into the numerator until the remainder is lower degree than the denominator • Example:

I. 3 The Laplace Transform • Continuous time • F(t) = 0, t < 0 • Transform a time function in another variable and then “untransform” • For the reasons of invariance of the solution, the “tag” is • Complex variable

This Laplace transform will exist so long as f(t) grows no faster than an exponential

• Region of analyticity Re (s) >= 0 • The properties for the Z-transform when Z=1 will correspond to properties for the Laplace transform when s=0

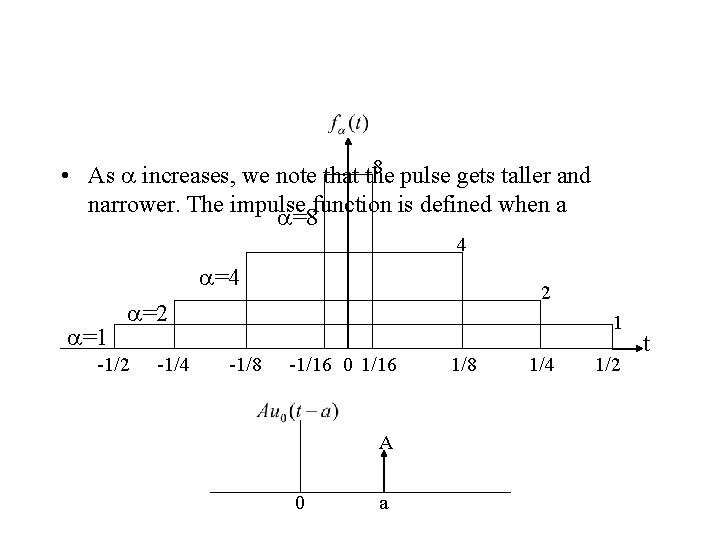
• A special case of our one sided exponential function when A=1, a=0 • Definition: • Function with area=1 and value >0, only with t=0

8 pulse gets taller and • As a increases, we note that the narrower. The impulse function is defined when a a=8 4 a=1 2 a=2 -1/4 1 -1/8 -1/16 0 1/16 A 0 a 1/8 1/4 1/2 t

• The “derivative” of the unit step function must therefore be a unit impulse function • Sifting property • Derivative of the unit impulse: unit doublet • Function is 0 everywhere, except in the vicinity of the origin it runs off to infinity just to the left of the origin and off to - infinity just to the right of the origin, and, in addition, has a total area equal to zero

• We can define • Inverse process of the integral

• Transform of the convolution Convolution definition:

The inspection method for inverse transforms

I. 4 Use of transforms in the solution of difference and differential equations • Solution of a differential equation Let us consider:

• Homogeneous and a particular solution: • Homogeneous solution: • General form of solution: where A and a are yet to be determined If we substitute the general solution into the equation, we find:

• Nth-order polynomial has N solutions: • Associated with each such solution is an which will be determined from the initial conditions (N conditions) • By canceling the common term then the solution is: • Solution: resolution of polynomial equation

• If there are no multiple roots, the homogenious solution is: • In case of non-distinct roots, the k equal roots will contribute to the following form: • Particular solution: guess from the form of Example:

• Second-order equation: exist for n=2, 3, 4, …There are two initial conditions, • Homogeneous solution: • Particular solution: must be guessed from

• Using the initial conditions, we find that

• Method of Z-transform for solving difference equations – Our approach begins by defining the Z-transform – Then we may apply our inversion techniques – Put G(Z) in evidence and the function is calculated by the inspection method Equation:

• Solution of constant-coefficient linear differential equations • Solution = homogeneous + particular • The form of the homogeneous solution will be:

• Solution of differential equations by the Laplace transform