Transformasi Z Transformasi Z dalam pengolahan sinyal digital

Transformasi Z • Transformasi Z dalam pengolahan sinyal digital mempunyai aturan yang sama dengan Transformasi Laplace pada rangkaian dan sistem analog. • Terdapat intuisi bahwa kadang tidak mudah menganalisis pada domain waktu. • Mempermudah operasi pada domain waktu, konvolusi pada domain waktu dipetakan ke perkalian pada domain Z. • Digunakan untuk mendefinisikan fungsi transfer • Digunakan untuk melihat respons sistem menggunakan proses table - look- up. 1. Definisi Transformasi Z sinyal waktu diskrit x(n) didefinisikan: z adalah variable kompleks Atau: X(Z) Z[x(n)] Hubungan antara x(n) dan X(z): Untuk deret kausal: 1 TE 4230 -Z Trans.

Karena transformasi Z merupakan deret yang tidak terbatas, hanya ada untuk harga z dimana deretnya konvergen. ROC (region of Convergence) X(z) adalah himpunan seluruh harga z dimana X(z) mempunyai harga terbatas. Oleh sebab itu pada Transformasi Z selalu juga ditentukan ROCnya. Contoh: Tentukan Transformasi Z untuk: x(n) = 2 n untuk n > 0 = 0 untuk n < 0 Ini merupakan deret geometri tidak terbatas, dimana : untuk A < 1 Tugas : 1. Tentukan X(z) dan daerah konvergensinya untuk: x(n) = (1/3)n u(n) untuk n > 0 = 0 untuk n < 0 2. Tentukan transformasi Z dan daerah konvergensi dari sinyal: x(n) = -an untuk n > 0 =0 untuk n < 0 2 TE 4230 -Z Trans.

3. 1. Sifat-sifat Transformasi Z Linieritas Jika dan Maka berlaku: Pergeseran deret Konvolusi Hitung konvolusi dari : x 1(n) = {1, -2, 1} x 2(n) = 1 0 < n < 5 = 0 selain itu jawaban: X 1(z) = 1 -2 z-1+ z-2 X 2(z) = 1+ z-2+ z-3+ z-4+ z-5 Sesuai dengan sifat konvolusi, maka: (z) X Jadi: = X 1(z)X 2(z) = 1 -z-6 -z-7 x(n) = {1, -1, 0, 0, -1, 1} Skala 3 TE 4230 -Z Trans.

2. Transformasi Z Inverse 7 TE 4230 -Z Trans.

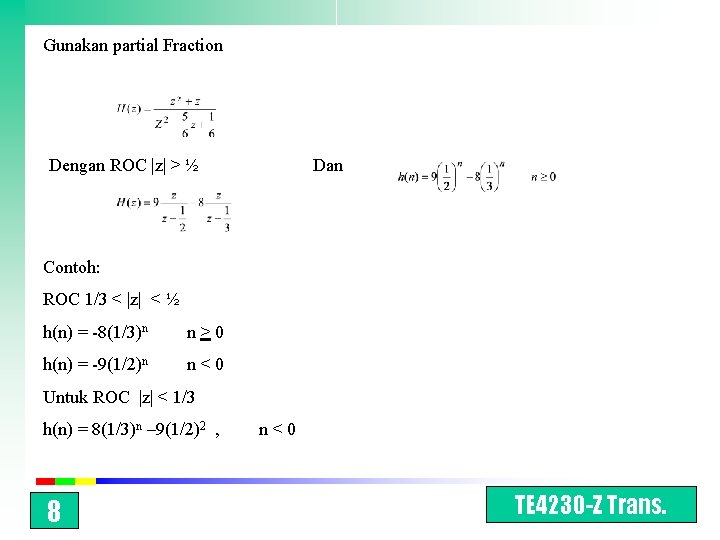
Gunakan partial Fraction Dengan ROC |z| > ½ Dan Contoh: ROC 1/3 < |z| < ½ h(n) = -8(1/3)n n > 0 h(n) = -9(1/2)n n < 0 Untuk ROC |z| < 1/3 h(n) = 8(1/3)n – 9(1/2)2 , 8 n < 0 TE 4230 -Z Trans.

2. 1 Invers Transformasi Z menggunakan teori Residu dibatasi pada deret kausal, transformasi Z: Jika integrasi berlawanan arah dengan jarum jam yang berada dalam ROC dan termasuk di dalam lingkaran satuan, maka. Jika dekat dengan origin: sehingga: Teori keadaan Residu Cauchy untuk polynomial rasional X(z) 9 TE 4230 -Z Trans.

Contoh: 10 TE 4230 -Z Trans.

2. 2 Mencari Respons Impulse menggunakan Invers Transformasi Z Akar persamaan Contoh: 11 TE 4230 -Z Trans.

Cari akar persamaannya, diperoleh: Dengan ROC |z| > ½ Respons Impulsenya adalah: Contoh: ROC 1/3 < |z| < ½ h(n) = -8(1/3)n n > 0 h(n) = -9(1/2)n n < 0 Untuk ROC |z| < 1/3 h(n) = 8(1/3)n – 9(1/2)2 , 12 n < 0 TE 4230 -Z Trans.

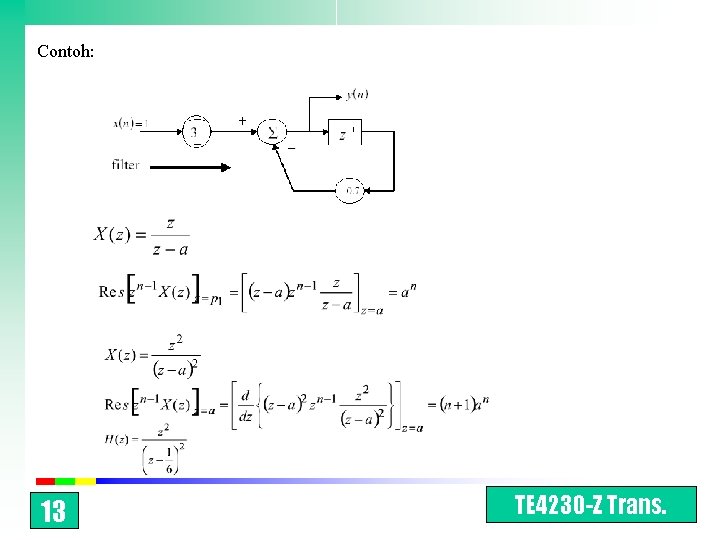
Contoh: 13 TE 4230 -Z Trans.

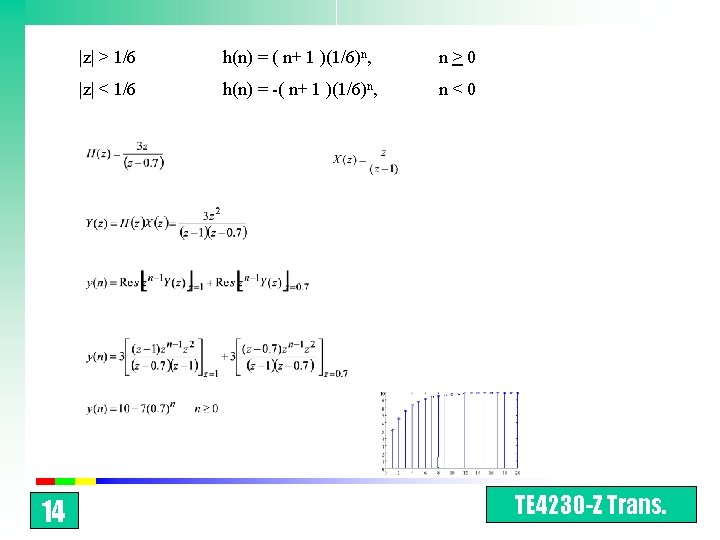
14 |z| > 1/6 h(n) = ( n+ 1 )(1/6)n, n > 0 |z| < 1/6 h(n) = -( n+ 1 )(1/6)n, n < 0 TE 4230 -Z Trans.