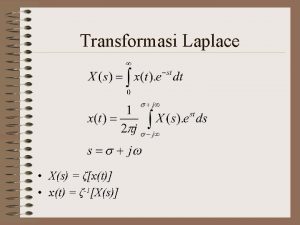EKT 119 ELECTRIC CIRCUIT II Chapter 2 Laplace







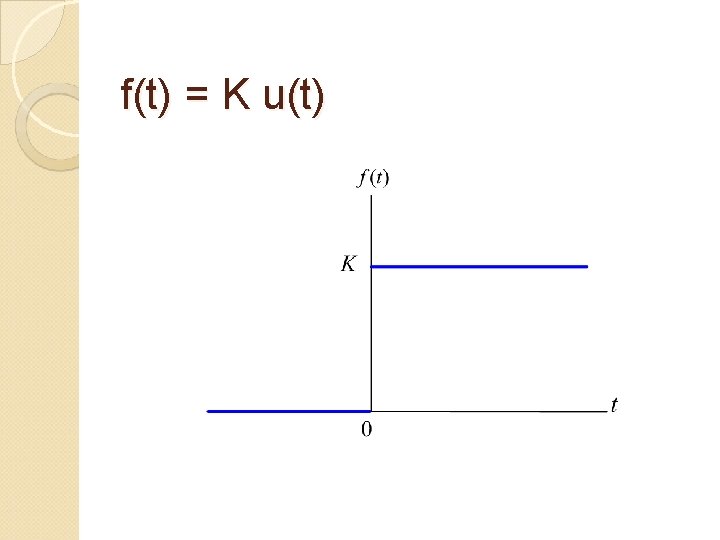

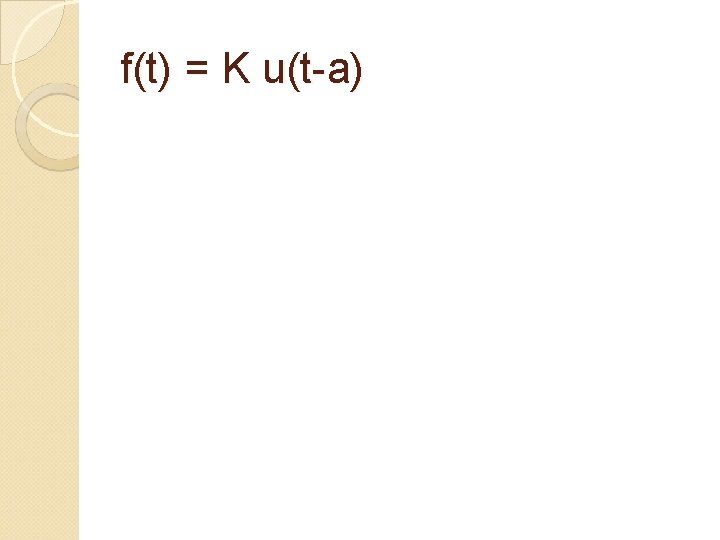


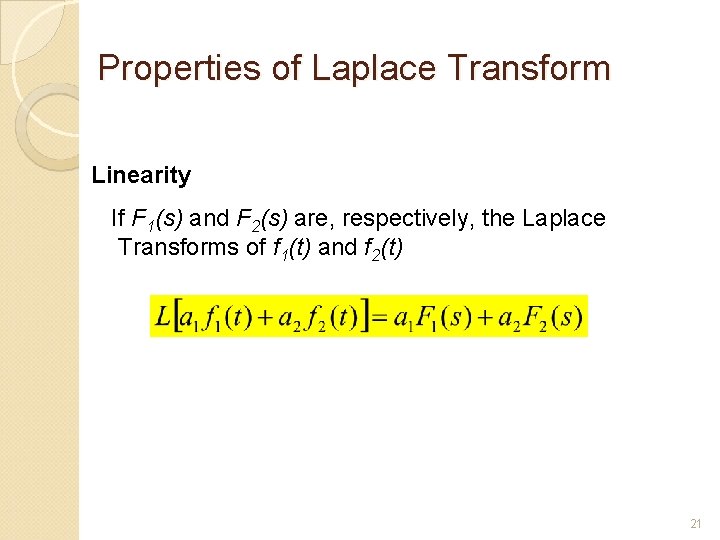






- Slides: 27

EKT 119 ELECTRIC CIRCUIT II Chapter 2 Laplace Transform SEM 1 2015/2016 1

Definition of Laplace Transform The Laplace Transform is an integral transformation of a function f(t) from the time domain into the complex frequency domain, giving F(s) s: complex frequency Called “The One-sided or unilateral Laplace Transform”. In the two-sided or bilateral LT, the lower limit is -. We do not use this.

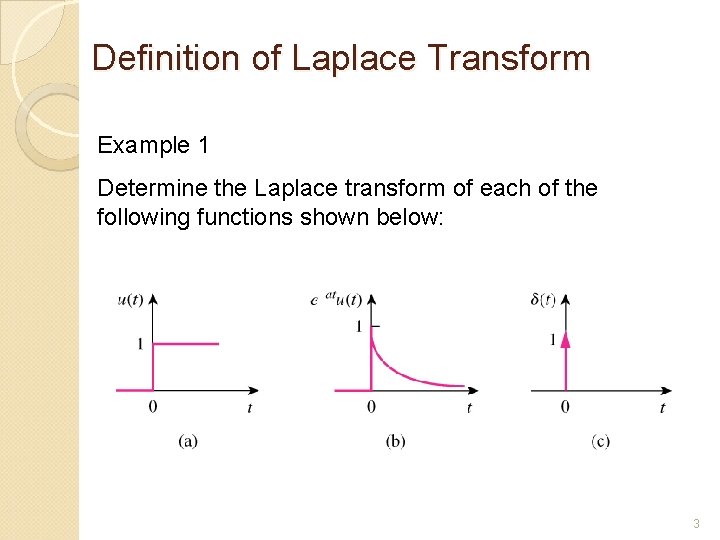
Definition of Laplace Transform Example 1 Determine the Laplace transform of each of the following functions shown below: 3

Definition of Laplace Transform Solution: a) The Laplace Transform of unit step, u(t) is given by 4

Definition of Laplace Transform Solution: b) The Laplace Transform of exponential function, e-atu(t), a>0 is given by 5

Definition of Laplace Transform Solution: c) The Laplace Transform of impulse function, δ(t) is given by 6

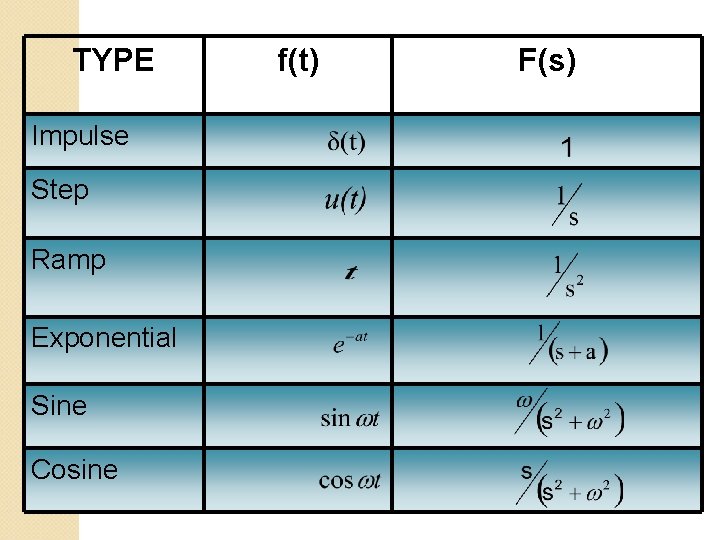
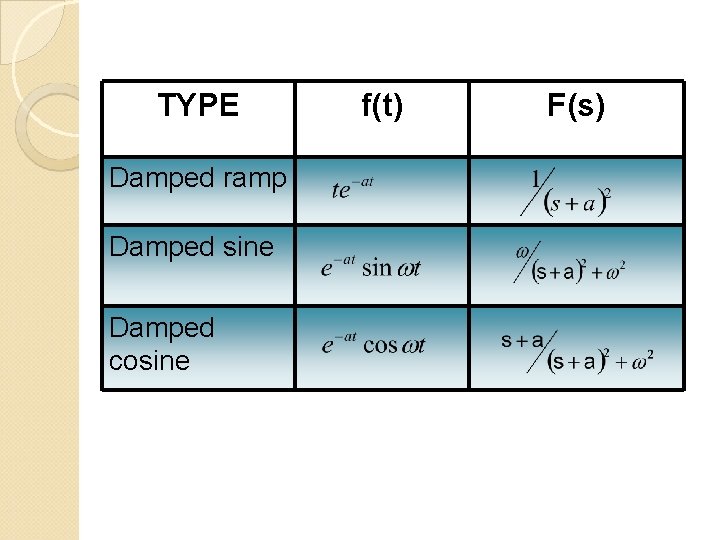
Functional Transform

TYPE Impulse Step Ramp Exponential Sine Cosine f(t) F(s)

TYPE Damped ramp Damped sine Damped cosine f(t) F(s)

Properties of Laplace Transform Step Function The symbol for the step function is K u(t). Mathematical definition of the step function:
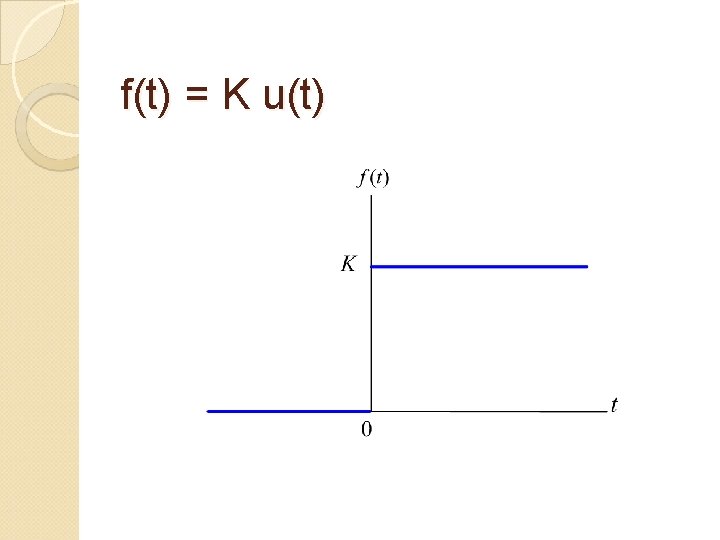
f(t) = K u(t)

Properties of Laplace Transform Step Function A discontinuity of the step function may occur at some time other than t=0. A step that occurs at t=a is expressed as:
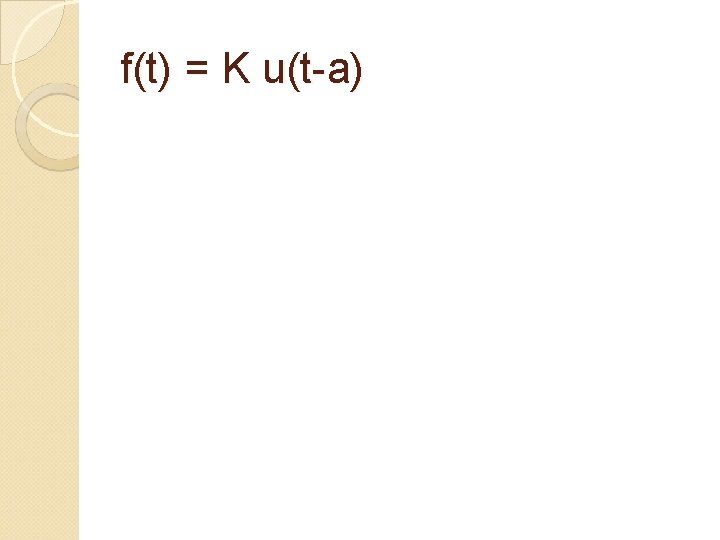
f(t) = K u(t-a)

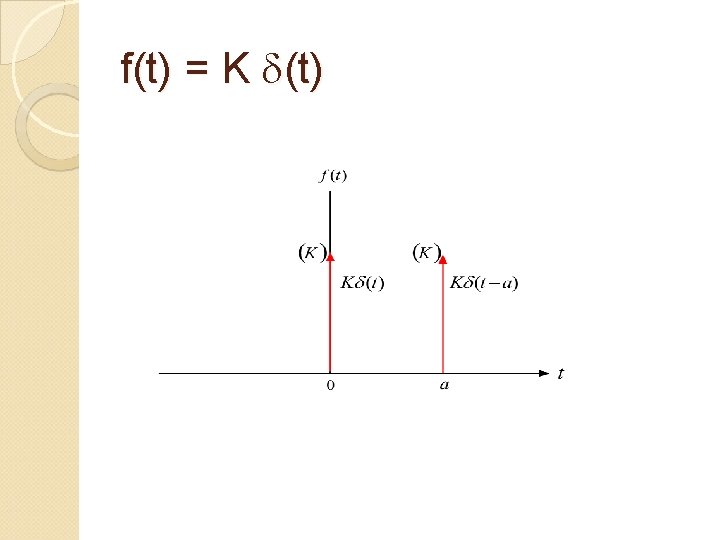
Properties of Laplace Transform Impulse Function symbol for the impulse function is (t). Mathematical definition of the impulse function: The

Properties of Laplace Transform Impulse Function The area under the impulse function is constant and represents the strength of the impulse. The impulse is zero everywhere except at t=0. An impulse that occurs at t = a is denoted K (t-a)

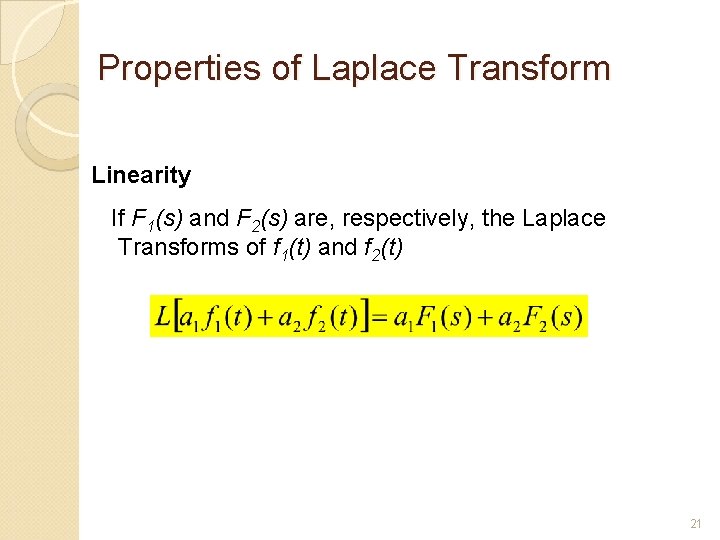
Properties of Laplace Transform Linearity If F 1(s) and F 2(s) are, respectively, the Laplace Transforms of f 1(t) and f 2(t) 21

Properties of Laplace Transform Scaling If F (s) is the Laplace Transforms of f (t), then 22

Properties of Laplace Transform Time Shift If F (s) is the Laplace Transforms of f (t), then 23

The Inverse Laplace Transform Suppose F(s) has the general form of The finding the inverse Laplace transform of F(s) involves two steps: 1. Decompose F(s) into simple terms using partial fraction expansion. 2. Find the inverse of each term by matching entries in Laplace Transform Table. 24

The Inverse Laplace Transform Example 1 Find the inverse Laplace transform of Solution: 25

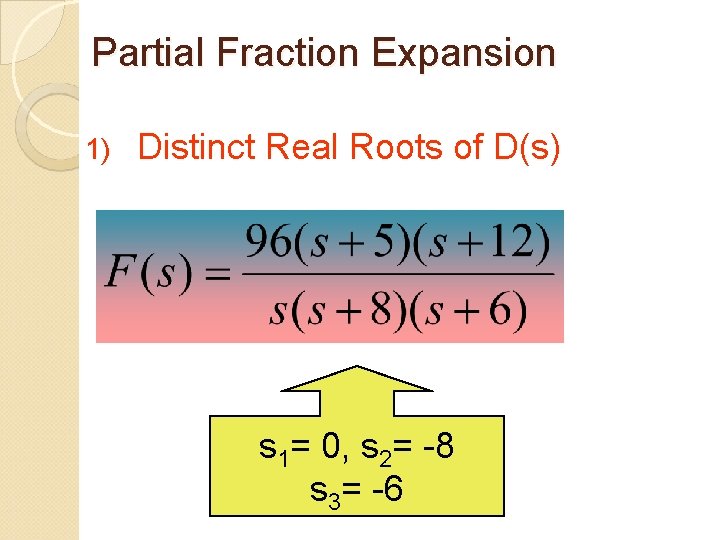
Partial Fraction Expansion 1) Distinct Real Roots of D(s) s 1= 0, s 2= -8 s 3= -6

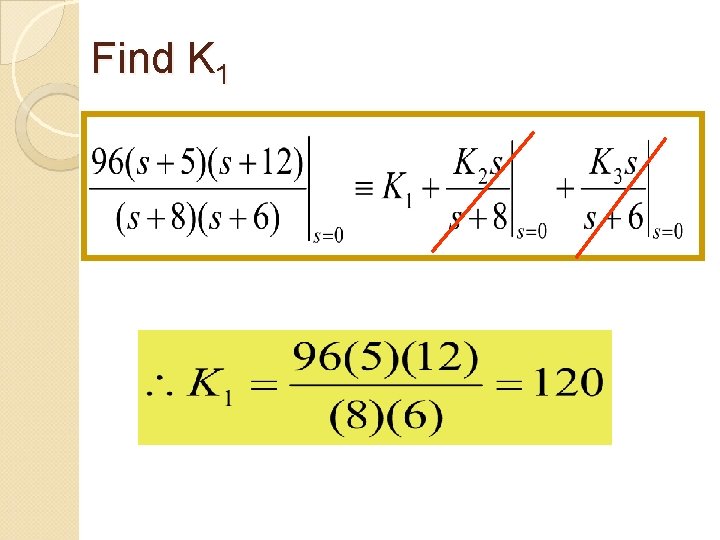
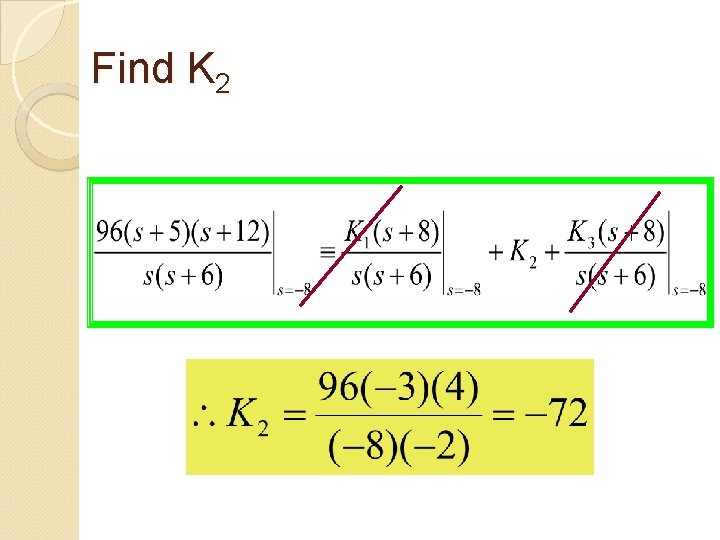
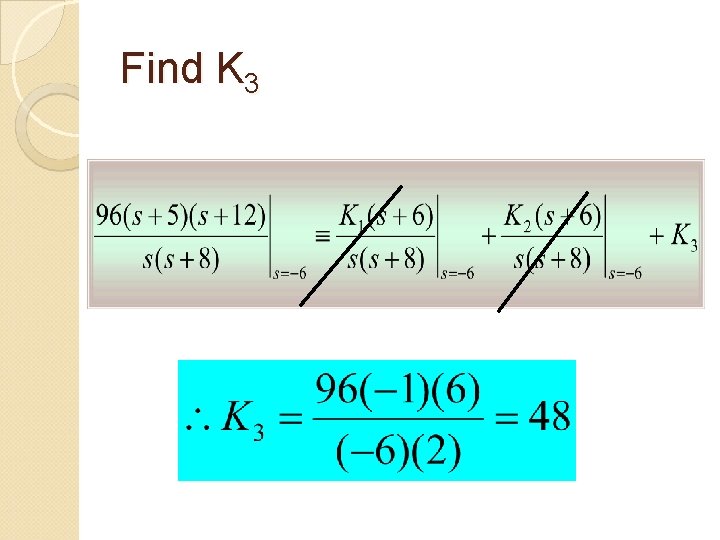
1) Distinct Real Roots To find K 1: multiply both sides by s and evaluates both sides at s=0 To find K 2: multiply both sides by s+8 and evaluates both sides at s=-8 To find K 3: multiply both sides by s+6 and evaluates both sides at s=-6

Find K 1

Find K 2

Find K 3

Inverse Laplace of F(s)
 Sam meek
Sam meek Kalkulationsberechnung
Kalkulationsberechnung S-domain circuit
S-domain circuit A suitable electric pump in an electric circuit is a
A suitable electric pump in an electric circuit is a Laplace table transform
Laplace table transform Chapter 21 electric charge and electric field
Chapter 21 electric charge and electric field Chapter 21 electric charge and electric field
Chapter 21 electric charge and electric field Coloumb units
Coloumb units Dc o/d per item charge
Dc o/d per item charge Chapter 23 electric current circuit happenings
Chapter 23 electric current circuit happenings Laplace equation electric field
Laplace equation electric field Laplace transform of inductance
Laplace transform of inductance Electric potential and electric field
Electric potential and electric field Electric potential due to a dipole
Electric potential due to a dipole Electric potential from electric field
Electric potential from electric field Electric potential and electric field
Electric potential and electric field Electric charges and electric forces lesson outline
Electric charges and electric forces lesson outline Circuit electric cu 3 becuri
Circuit electric cu 3 becuri Draw a simple electric circuit and label the parts
Draw a simple electric circuit and label the parts Derive ohms law
Derive ohms law Node branch
Node branch Membuat desain konstruksi instalasi listrik rumah tangga
Membuat desain konstruksi instalasi listrik rumah tangga Phet electric circuits
Phet electric circuits Analogy circuit
Analogy circuit Analogy between electric and magnetic circuit
Analogy between electric and magnetic circuit Draw and label the parts of basic electrical circuit
Draw and label the parts of basic electrical circuit Principles of electronic circuits
Principles of electronic circuits Electric circuit elements
Electric circuit elements