Aperiodic Tilings Alexandre Karassev Tilings A tiling or

Aperiodic Tilings Alexandre Karassev

Tilings • A tiling (or tessellation) is a cover of the plane (or space) by nonoverlaping regions

Tilings in nature

Escher’s tilings http: //www. mcescher. com/

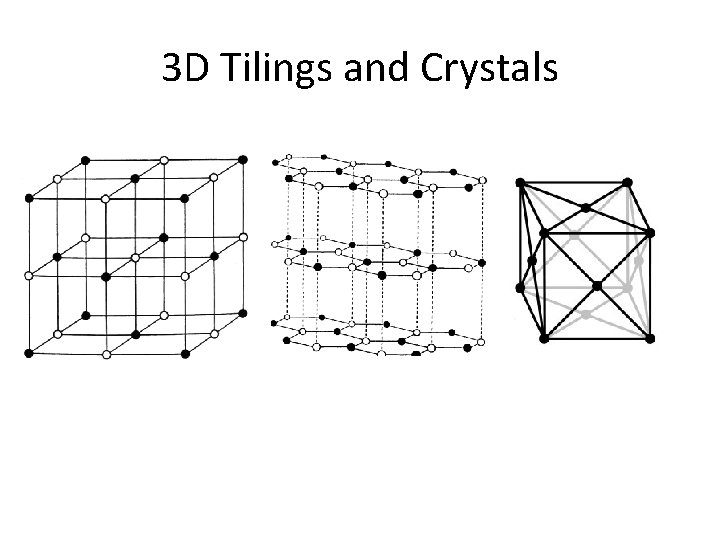
3 D Tilings and Crystals

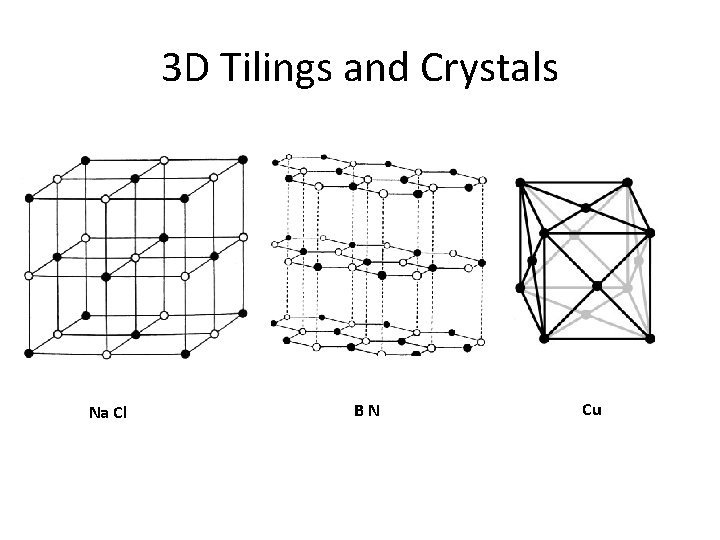
3 D Tilings and Crystals Na Cl BN Cu

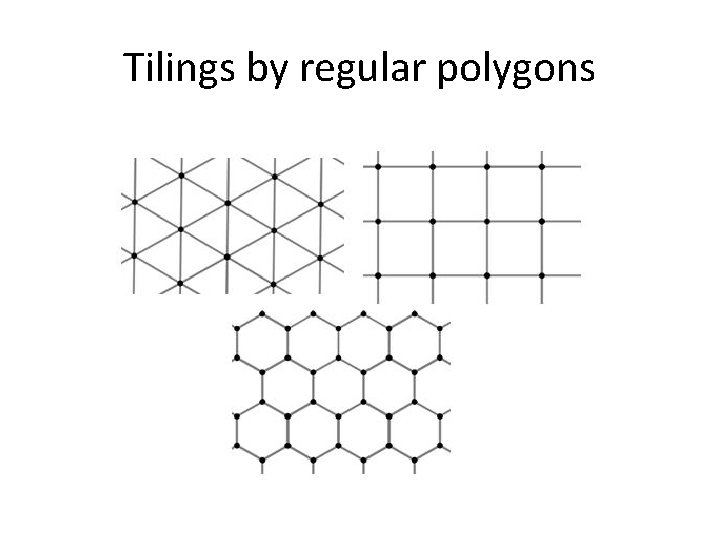
Tilings by regular polygons

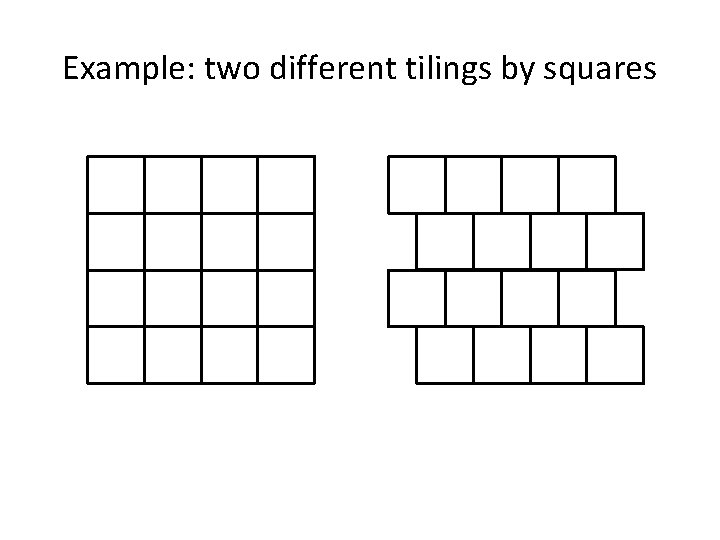
Tiles • A tile is a polygonal region of the plane (not necessarily convex) • Two tiles are called – identical (congruent) if one can be transformed to the other by shift and rotation – of the same type (or similar), if one is a rescaling of the other Identical tiles Tiles of the same type

Example: two different tilings by squares

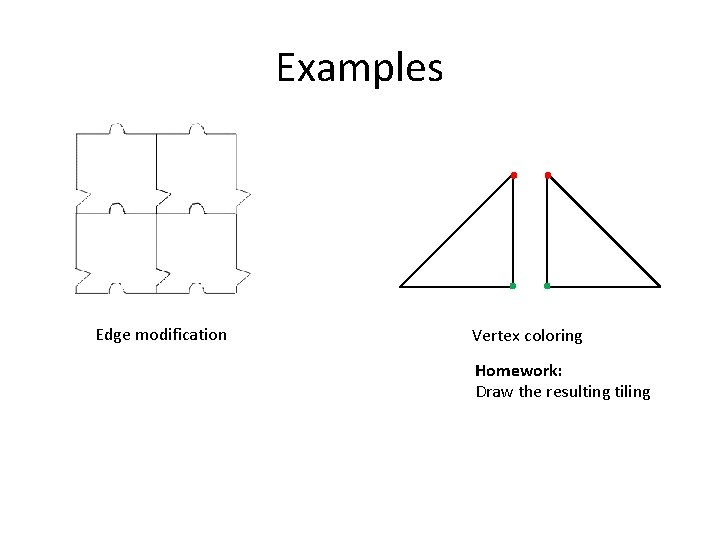
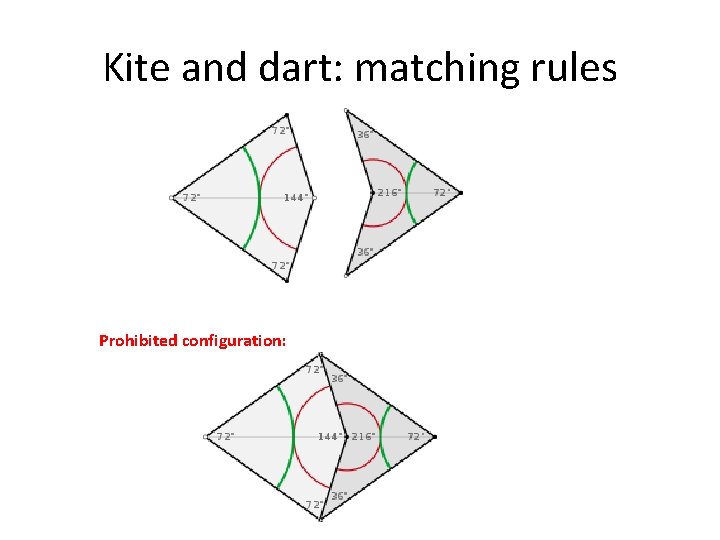
Matching rules • Matching rules specify a way of joining individual tiles (e. g. edge to edge matching) • Matching rules can be enforced in a number of ways, including: – vertex labeling or coloring – edge modifications

Examples Edge modification Vertex coloring Homework: Draw the resulting tiling

Homework • Any triangle can tile the plane • Any quadrilateral (even non-convex) can tile the plane • Which pentagons can tile the plane? Find at least one • Find a convex tile that can tile the plane in exactly one way • Can a regular tetrahedron tile the space? What about other regular polyhedra? • What about a non-regular tetrahedron?

Periodic and non-periodic tilings • A tiling is called periodic if it can be shifted to perfectly align with itself in at least two nonparallel directions • A tiling is called non-periodic if it cannot be shifted to perfectly align with itself • Do non-periodic tilings exist?

Trivial example

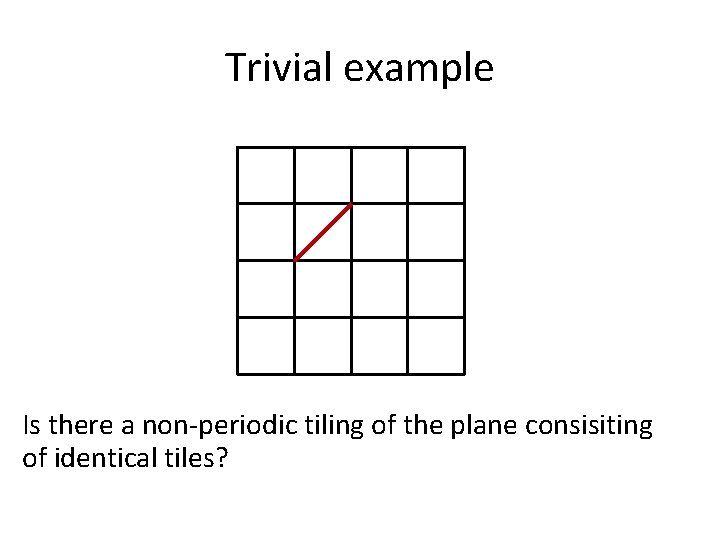
Trivial example Is there a non-periodic tiling of the plane consisiting of identical tiles?

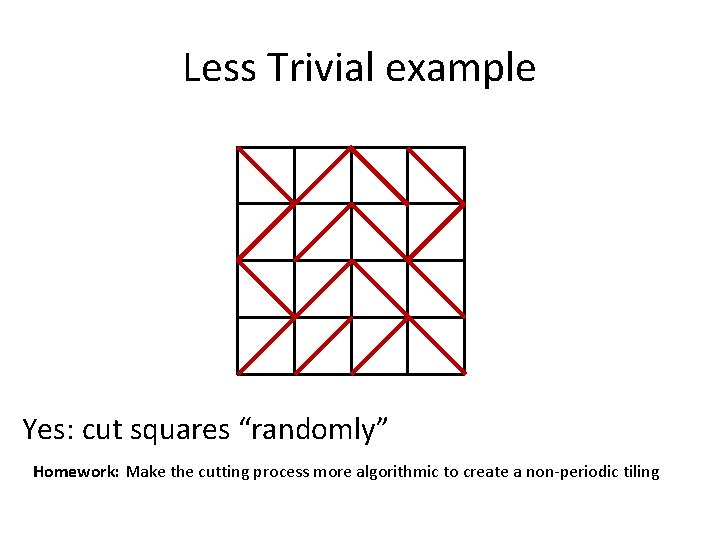
Less Trivial example Yes: cut squares “randomly” Homework: Make the cutting process more algorithmic to create a non-periodic tiling

Homework • Find other examples of non-periodic tilings by copies of a single triangle • Can non-periodic tilings be created using copies of a single square? What about rectangles?

Source of more interesting examples: substitution tilings • A partial tiling of the plane consisting of finitely many tiles is called a patch • Let S be a finite set of distinct tiles and S’ is a set of bigger (inflated) tiles, similar to those from S under the same rescaling • Suppose that each tile in S’ can be cut into a finite number of tiles that belong to S • Let P be a patch consisting of tiles from S • Rescale (inflate) P and then cut each tile in P to produce bigger patch that still uses tiles from S

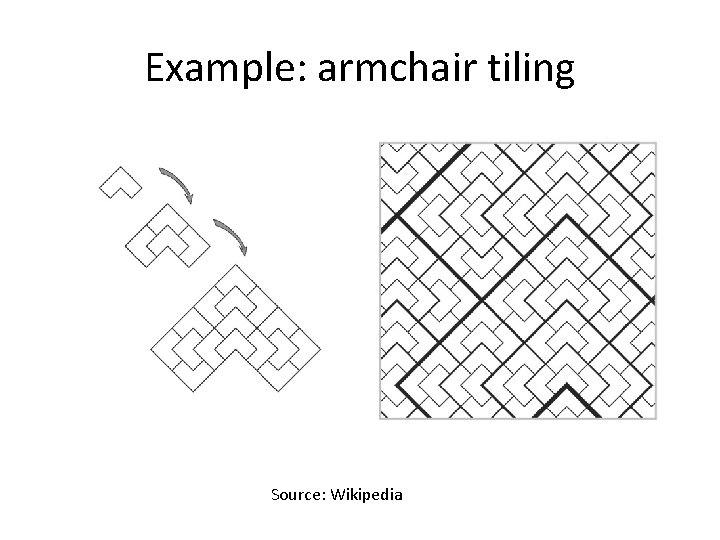
Example: armchair tiling Source: Wikipedia

Why is the armchair tiling non-periodic? Theorem If, in a substitution tiling, every next generation of tiles can be composed back into larger tiles in a unique way, the resulting tiling of the plane is non-periodic

Another example Source: Wikipedia

Conway’s pinwheel tiling (explicitly described by Charles Radin in 1994) John Conway

Why is the pinwheel tiling non-periodic? Theorem In the pinwheel tiling, every triangle appears rotated in infinitely many ways (reason: the angle arctan (1/2) is not a rational multiple of pi)

Nevertheless… • The armchair and two Conway’s triangles can also tile plane periodically • Are there finite sets of tiles that can tile plane only non-periodically? • Such finite sets of tiles are called aperiodic and the resulting tilings are called aperiodic tilings

Wang’s Conjecture and Discovery of Aperiodic Tilings • Conjecture (Wang, 1961): if a set of tiles can tile the plane, then they can always be arranged to do so periodically • Berger (1966): conjecture is false, and thus aperiodic tiles exist (first set contained 20, 426 tiles)

Smaller sets of aperiodic tiles • Raphael Robinson, 1971: 6 tiles • Roger Penrose, 1973 : discovery of sets containing 2 tiles • More small sets where also found by Robert Ammann • Unsolved Problem: does there exist one aperiodic tile?

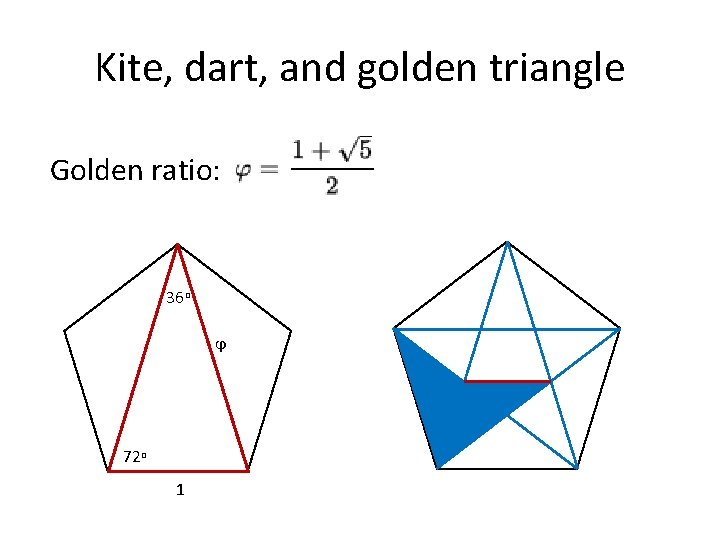
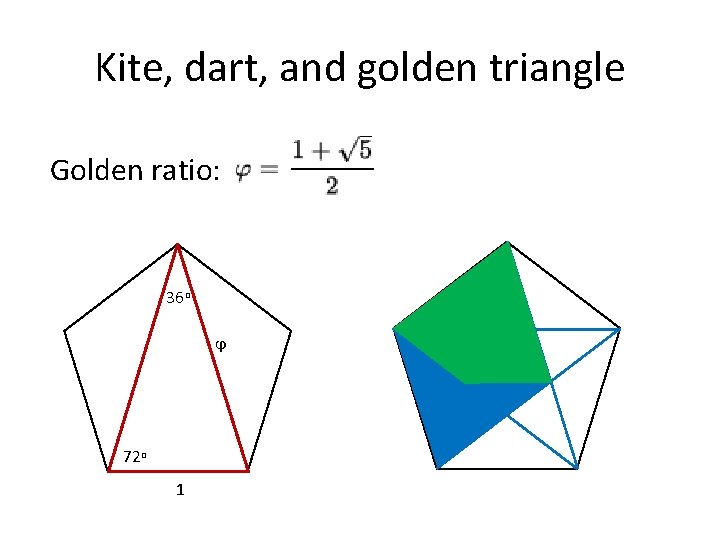
Penrose Tiles and Tilings • Pentagons, “diamond”, “boat”, “star” • Two rhombuses • “Kite” and “dart” Sir Roger Penrose

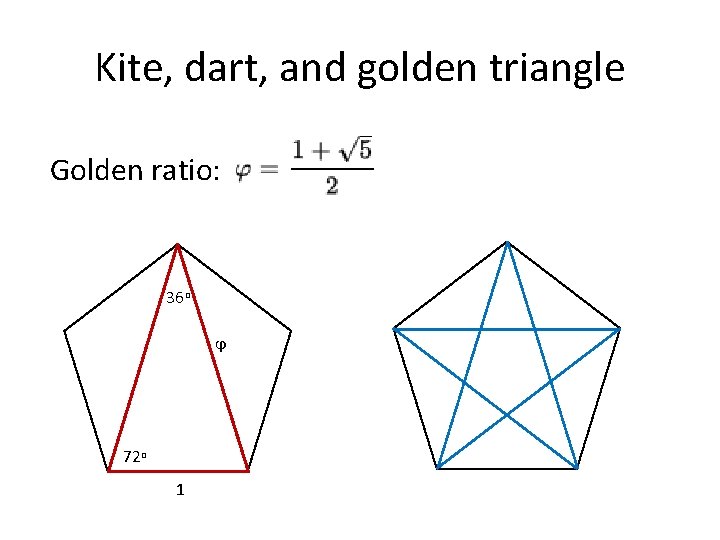
Kite, dart, and golden triangle Golden ratio: 36 o ϕ 72 o 1

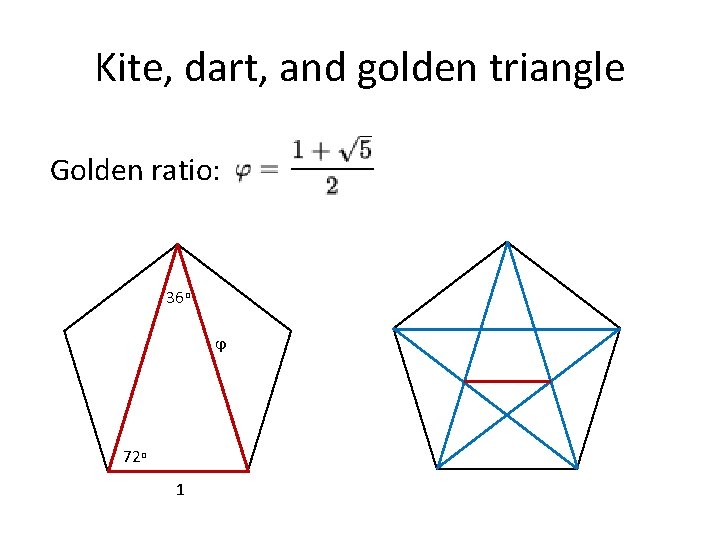
Kite, dart, and golden triangle Golden ratio: 36 o ϕ 72 o 1

Kite, dart, and golden triangle Golden ratio: 36 o ϕ 72 o 1

Kite, dart, and golden triangle Golden ratio: 36 o ϕ 72 o 1

Kite and dart: matching rules Prohibited configuration:

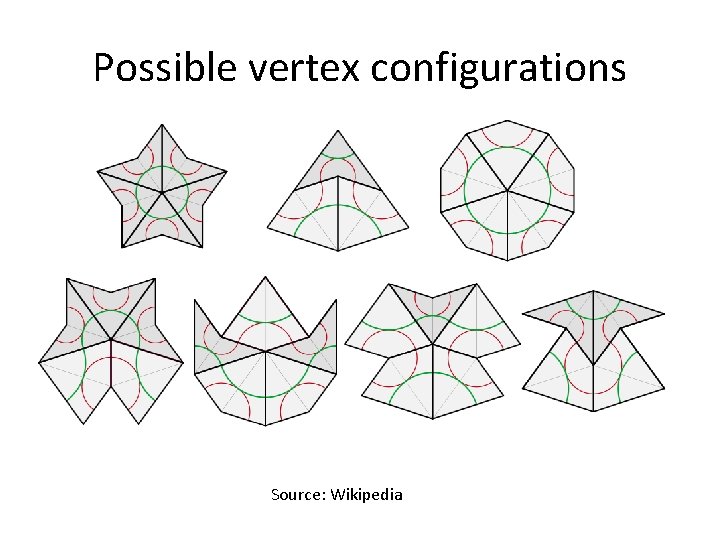
Possible vertex configurations Source: Wikipedia

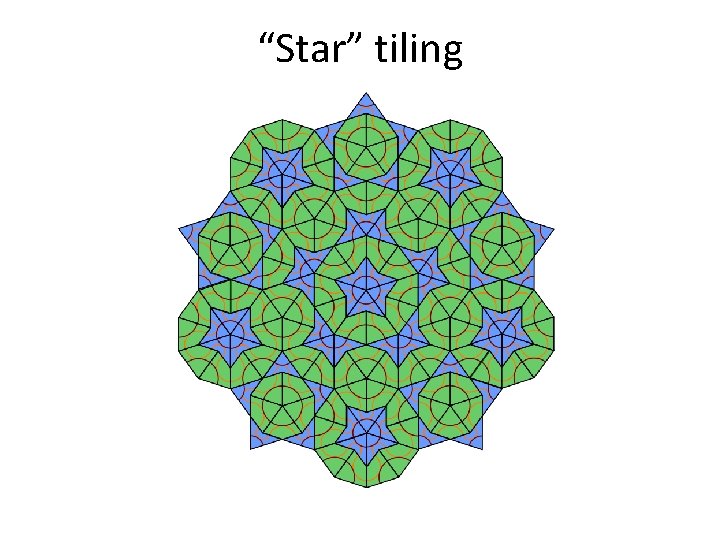
“Star” tiling

Kite and dart are aperiodic Theorem Any tiling of the plane by kites and darts that follows matching rules is aperiodic

Why can we tile the whole plane? • Extension theorem Let S be a finite set of tiles and let Dn denote the disc of radius n centered at the origin. Suppose that for any n there exists a patch Sn conisting of tiles from S such that Sn covers Dn. Then tiles from S can tile the whole plane. • Note: patches Sn do not have to be extensions of each other, and moreover, do not have to be related in any other way!

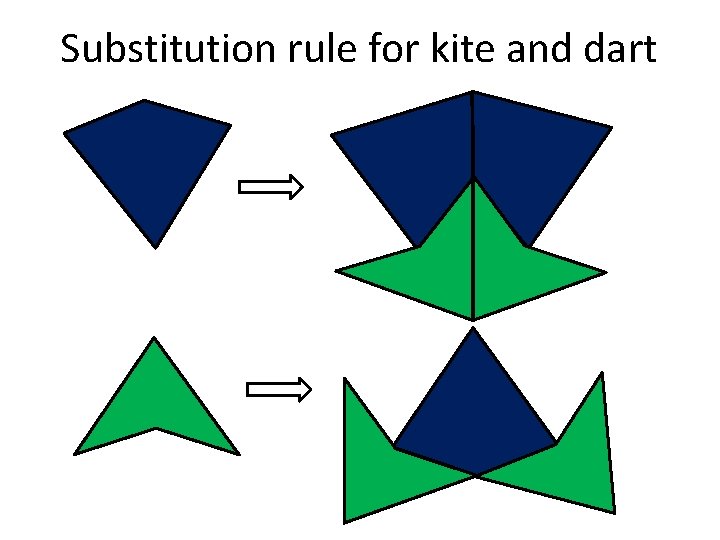
Substitution rule for kite and dart

Applying it to kite and dart • We need to show that • This can be done kites and darts can tile through the process of arbitrary large regions substitution and of the plane deflation/inflation Source: Wikipedia

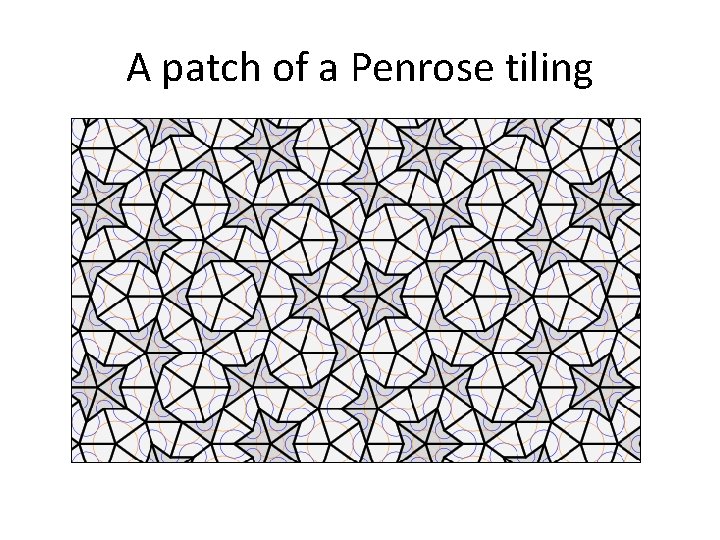
A patch of a Penrose tiling

Application of aperiodic tilings: quasicrystals In 1984 Dan Shechtman announced the discovery of new type of crystal-like structure

Quasicrystals • In 1984 Dan Shechtman announced the discovery of a material which produced a sharp diffraction pattern with a fivefold symmetry • This type of rotational symmetry is prohibited by crystallographic restrictions for usual (periodic) crystals, and thus the new material must be “aperiodic crystal” • Previously (in 1975) Robert Ammann had extended the Penrose construction to a three-dimensional icosahedral equivalent • Since Schehtman’s discovery, hundreds of different types of quasicrystals were found, including naturally occurring ones • Schehtman received Nobel prize in Chemistry in 2011

Thank you! • Questions faculty. nipissingu. ca/alexandk@nipissingu. ca