An Algorithm for the Consecutive Ones Property Claudio

An Algorithm for the Consecutive Ones Property Claudio Eccher

Outline 1. C 1 P definition 2. Biological background • Hybridization mapping 3. An algorithm for the C 1 P problem • Dividing in components • Taking care of a component • Joining the components together

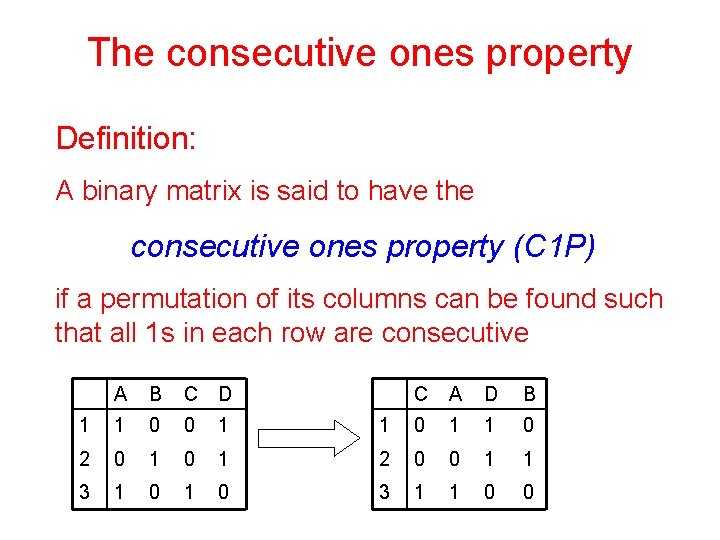
The consecutive ones property Definition: A binary matrix is said to have the consecutive ones property (C 1 P) if a permutation of its columns can be found such that all 1 s in each row are consecutive A B C D C A D B 1 1 0 0 1 1 0 2 0 1 2 0 0 1 1 3 1 0 3 1 1 0 0

The consecutive ones property Observation: the C 1 P is closed under taking submatrices A bad matrix: C A D 1 0 1 1 2 1 0 1 3 1 1 0 Whichever column x I put in the middle there is a row in which x is 0 Hence, every matrix containing this submatrix is ‘bad’

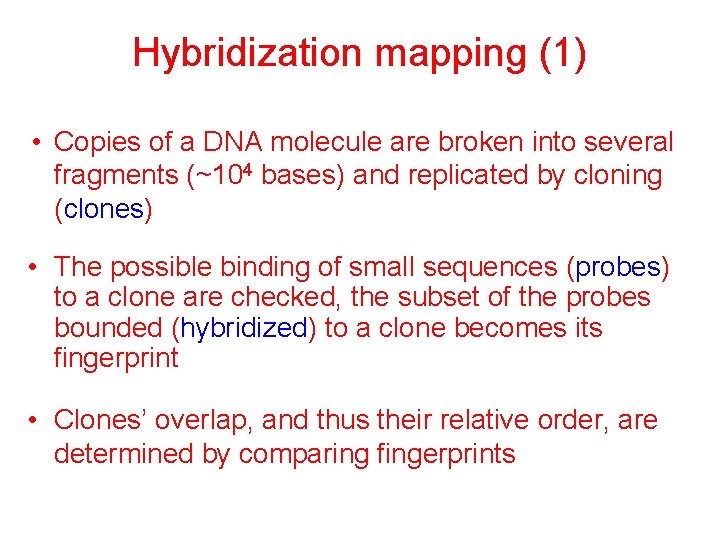
Hybridization mapping (1) • Copies of a DNA molecule are broken into several fragments (~104 bases) and replicated by cloning (clones) • The possible binding of small sequences (probes) to a clone are checked, the subset of the probes bounded (hybridized) to a clone becomes its fingerprint • Clones’ overlap, and thus their relative order, are determined by comparing fingerprints

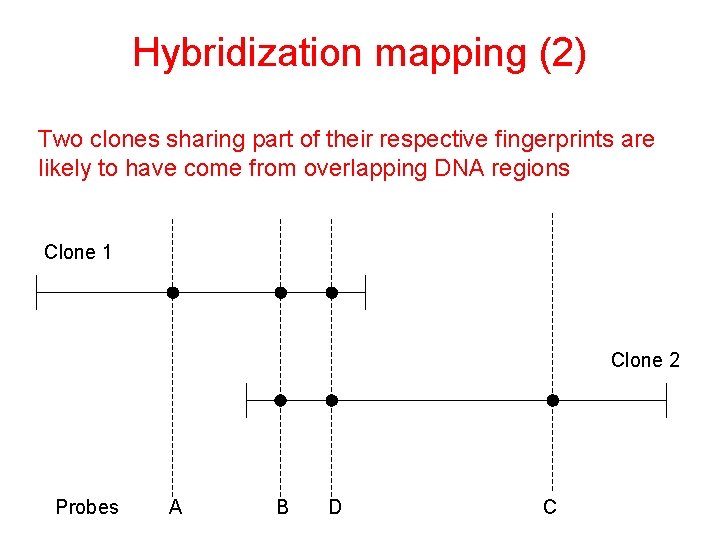
Hybridization mapping (2) Two clones sharing part of their respective fingerprints are likely to have come from overlapping DNA regions Clone 1 Clone 2 Probes A B D C

Assumptions • Probes are unique • There are no errors • All “clones x probes” hybridization experiments have been done

Model • n clones and m probes • n x m binary matrix M built from experimental data § Mij = 1 ðprobe j hybridized to clone i § Mij = 0 ðprobe j not hybridized to clone i

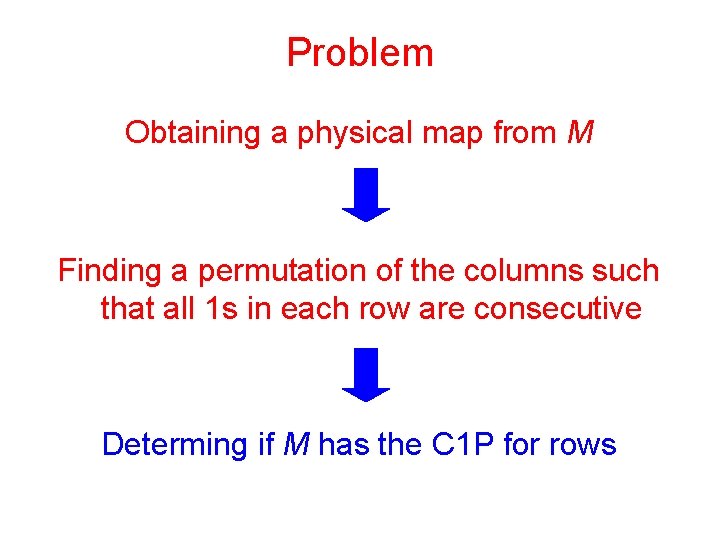
Problem Obtaining a physical map from M Finding a permutation of the columns such that all 1 s in each row are consecutive Determing if M has the C 1 P for rows

An algorithm for the C 1 P problem • The problem belongs to P • The algorithm is from Fulkerson and Gross (1965) Without loss of generality we can assume that: • All rows are different • No row is all zeros

Algorithm sketch Separation of the rows into components (subsets of rows) Permutation of the columns of each component Join of the components together

Row relations Definition: " row iÎM, Si={columns k | Mi, k=1} Given two rows i and j: 1. Si Ç Sj = Æ or 2. Si Í Sj or Sj Í Si or 3. Si Ç Sj ¹ Æ and none of them is a subset of the other

Dividing in components (1) Let’s initially lump together in the same component the rows with non empty intersection If $ a row k s. t. : Sk Ç Si = Æ or Sk Í Si " i ¹ k in this component Then row k can be put in its own component

Dividing in components (2) A graph Gc = (V, E) is built from matrix M • Each vertex V is a row of M • There is an undirected edge E from Vi to Vj if Si Ç Sj ¹ Æ and none of them is a subset of the other The components we want are the connected components of Gc

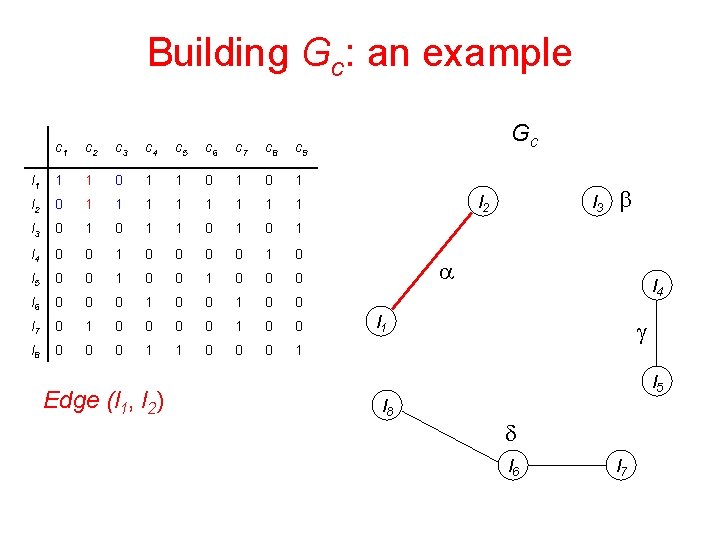
Building Gc: an example c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 l 1 1 1 0 1 0 1 l 2 0 1 1 1 1 l 3 0 1 1 0 1 l 4 0 0 1 0 l 5 0 0 1 0 0 0 l 6 0 0 0 1 0 0 l 7 0 1 0 0 l 8 0 0 0 1 1 0 0 0 1 Edge (l 1, l 2) Gc l 2 l 3 b a l 4 l 1 g l 5 l 8 d l 6 l 7

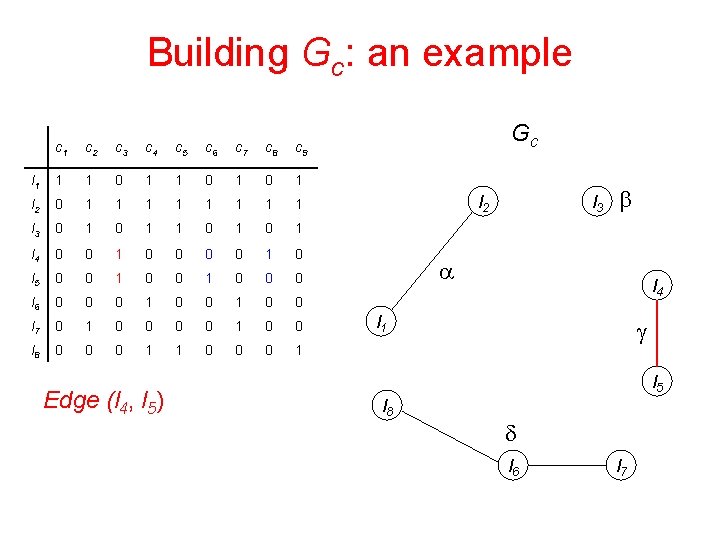
Building Gc: an example c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 l 1 1 1 0 1 0 1 l 2 0 1 1 1 1 l 3 0 1 1 0 1 l 4 0 0 1 0 l 5 0 0 1 0 0 0 l 6 0 0 0 1 0 0 l 7 0 1 0 0 l 8 0 0 0 1 1 0 0 0 1 Edge (l 4, l 5) Gc l 2 l 3 b a l 4 l 1 g l 5 l 8 d l 6 l 7

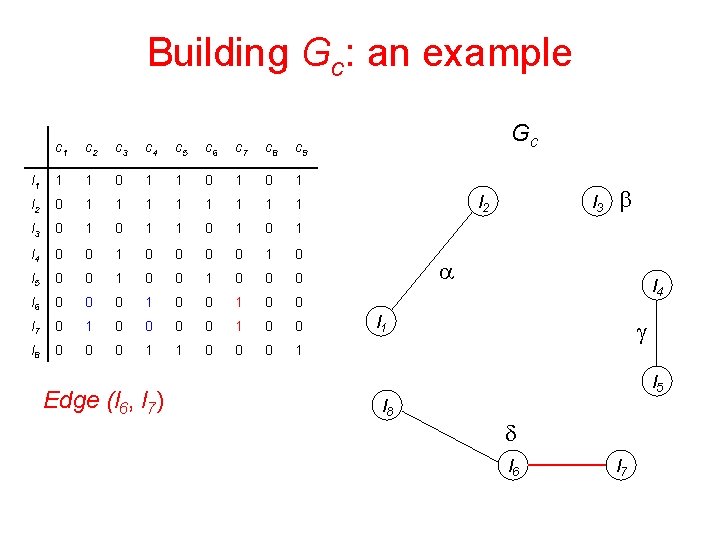
Building Gc: an example c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 l 1 1 1 0 1 0 1 l 2 0 1 1 1 1 l 3 0 1 1 0 1 l 4 0 0 1 0 l 5 0 0 1 0 0 0 l 6 0 0 0 1 0 0 l 7 0 1 0 0 l 8 0 0 0 1 1 0 0 0 1 Edge (l 6, l 7) Gc l 2 l 3 b a l 4 l 1 g l 5 l 8 d l 6 l 7

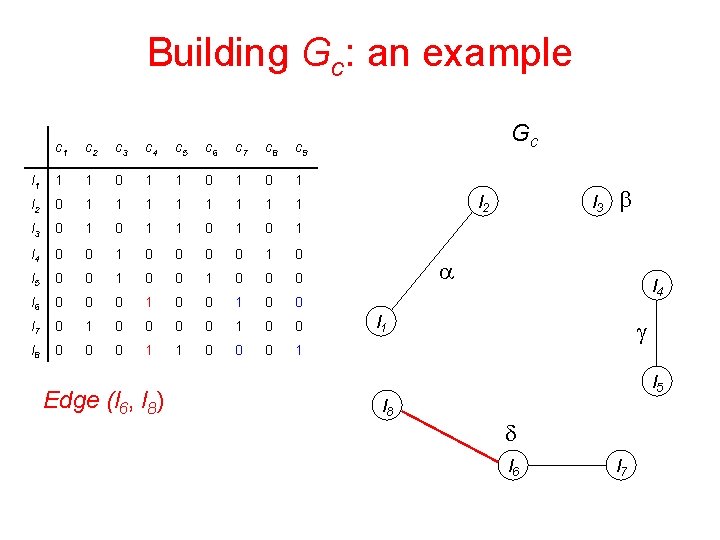
Building Gc: an example c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 l 1 1 1 0 1 0 1 l 2 0 1 1 1 1 l 3 0 1 1 0 1 l 4 0 0 1 0 l 5 0 0 1 0 0 0 l 6 0 0 0 1 0 0 l 7 0 1 0 0 l 8 0 0 0 1 1 0 0 0 1 Edge (l 6, l 8) Gc l 2 l 3 b a l 4 l 1 g l 5 l 8 d l 6 l 7

Taking care of a component (1) c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 l 1 0 0 0 0 1 1 l 2 0 1 0 1 0 l 3 1 0 0 1 1 l 2 l 3 The 1 s of the first row have to be put consecutive. The possible solutions can be represented as follows: l 1 … 0 {2, 7, 8} 1 0 … The second row is adjacent to the first one. Hence, for the second row (l 2) there are 2 choices: the 1 s can be placed to the left or to the right of those of the row l 1. In any case the direction does not really matter l 1 l 2 … … 0 0 {5} 0 1 {2, 7} 1 1 {8} 1 0 0 0 … …

Taking care of a component (2) c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 l 1 0 0 0 0 1 1 l 2 0 1 0 1 0 l 3 1 0 0 1 1 l 2 l 3 For the third row (l 3) we have to consider the relations with the rows connected by edges to l 3 Let’s place l 3 with respect to l 2: we cannot place l 3 in either direction (left or right) because of its relation with l 1 To take into account the relation between l 1 and l 3 is necessary to consider the number of elements in the intersections between S 1, S 2 and S 3

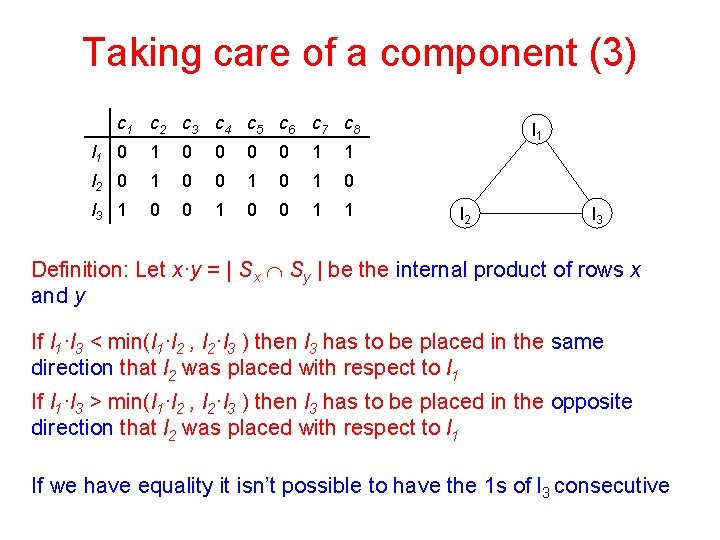
Taking care of a component (3) c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 l 1 0 0 0 0 1 1 l 2 0 1 0 1 0 l 3 1 0 0 1 1 l 2 l 3 Definition: Let x·y = | Sx Ç Sy | be the internal product of rows x and y If l 1·l 3 < min(l 1·l 2 , l 2·l 3 ) then l 3 has to be placed in the same direction that l 2 was placed with respect to l 1 If l 1·l 3 > min(l 1·l 2 , l 2·l 3 ) then l 3 has to be placed in the opposite direction that l 2 was placed with respect to l 1 If we have equality it isn’t possible to have the 1 s of l 3 consecutive

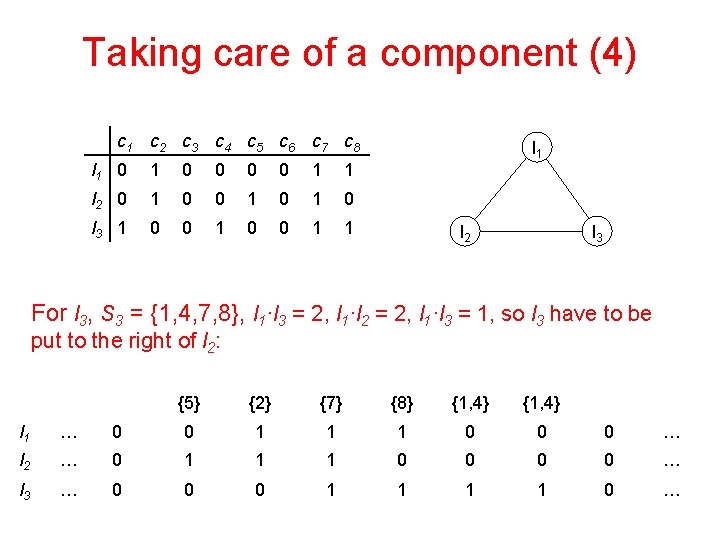
Taking care of a component (4) c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 l 1 0 0 0 0 1 1 l 2 0 1 0 1 0 l 3 1 0 0 1 1 l 2 l 3 For l 3, S 3 = {1, 4, 7, 8}, l 1·l 3 = 2, l 1·l 2 = 2, l 1·l 3 = 1, so l 3 have to be put to the right of l 2: {5} {2} {7} {8} {1, 4} l 1 … 0 0 1 1 1 0 0 0 … l 2 … 0 1 1 1 0 0 … l 3 … 0 0 0 1 1 0 …

Taking care of a component (5) The only choice made was in the placement of l 2 with respect to l 1 and both possibilities result in the same solutions up to reversal. We had no choice in placing l 3 Therefore, if the component has the C 1 P, then l 1 and l 3 must result properly placed If, on the contrary, l 1 and l 3 are not properly placed, then we conclude that the component (and hence the matrix) doesn’t have the C 1 P

String generator We have seen the following examples of string generator {2, 7, 8} {{5} {2, 7} {8}} {{5} {2} {7} {8} {1, 4}} A permutation p of the probes is compatible with a string generator if whenever A, B, C appear in this order in p and A and C are in a group G, then B is also included in G An invariant of the algorithm is that, after considering rows 1. . k, a permutation p certificates the C 1 P of the submatrix on rows 1. . k iff either p or its reversal is compatible with the string generator

Taking care of a component: a ‘bad’ component c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 l 1 0 1 1 0 0 0 1 1 l 2 0 1 0 1 0 l 3 1 0 0 1 1 l 2 l 3 l 1 … 0 {5} 0 l 2 … 0 1 … … … 0 0 0 {5} 0 1 0 {2} 1 1 0 The relations between the rows are the same as the preceding component {2, 7} 1 {8, 3} 1 0 … 1 0 0 … {7} 1 1 1 {8} 1 0 1 {3} 1 0 0 {1, 4} 0 0 1 … … …

Taking care of a component (6) For a new row k in the same component find two previously placed rows i and j s. t. $ E(k, i), E(i, j) in Gc and proceed as for the three-row case. Check also the consistency with the solution generator The algorithm gives all possible permutations of a component having the C 1 P, up to reversal

Algorithm implementation Construct Gc and traverse it using depth-first search When visiting a vertex invoke procedure Place Algorithm Place input: u, v, w vertices of Gc=(V, E) s. t. (u, v)ÎE and (v, w) ÎE output: A placement for row u, if possible if v = nil and w = nil then Place all 1 s of u consecutively else if w = nil then Left- or right-place the 1 s of u with respect to the 1 s of v Record direction used else if u · w < min(u · v , v · w) then Place u with respect to v in the same direction used in v, w placement. Record direction used else Place u with respect to v in the opposite direction used in v, w placement. Record direction used Check consistency of column set If column sets are not consistent then the component doesn’t have the C 1 P

Algorithm running time For a n x m matrix building graph Gc takes O(nm) time To check consistency of column sets requires O(m) time per row and there are n rows to process Total time is thus O(nm)

Joining components together (1) Construct a new graph GM = (V, E) in which: • Each component ak of M is a vertex in GM • For a, bÎV, there is a directed edge from a to b if " row iÎb sets Si are contained in at least one set Sj of a GM tells us how the components of M fit together

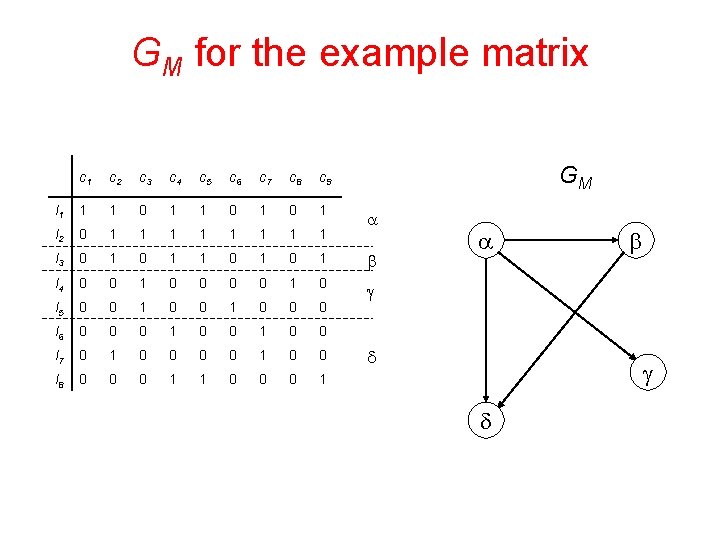
GM for the example matrix GM c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 l 1 1 1 0 1 0 1 l 2 0 1 1 1 1 l 3 0 1 1 0 1 b l 4 0 0 1 0 l 5 0 0 1 0 0 0 g l 6 0 0 0 1 0 0 l 7 0 1 0 0 l 8 0 0 0 1 1 0 0 0 1 a a d b g d

Joining components together (2) For two sets Si Î b, Sj Îa, if Si Í Sj then there is no row k Î a s. t. Si Ë Sk and Si Ç Sk ¹ Æ The exact same containments and disjunctions hold for all other sets from b GM is acyclic

Joining components together (3) The joining of components depends on the way sets in one component contain or are contained in sets from other components Components having sets not contained anywhere else should be processed first Containment is specified by the directed edges in GM

Joining components together (4) GM has to be processed in topological order Remove all sources from GM (e. g. a) and make the union of their string generators While GM is not empty take the next source b, remove b from GM, and refine the current string generator with the string generator of b

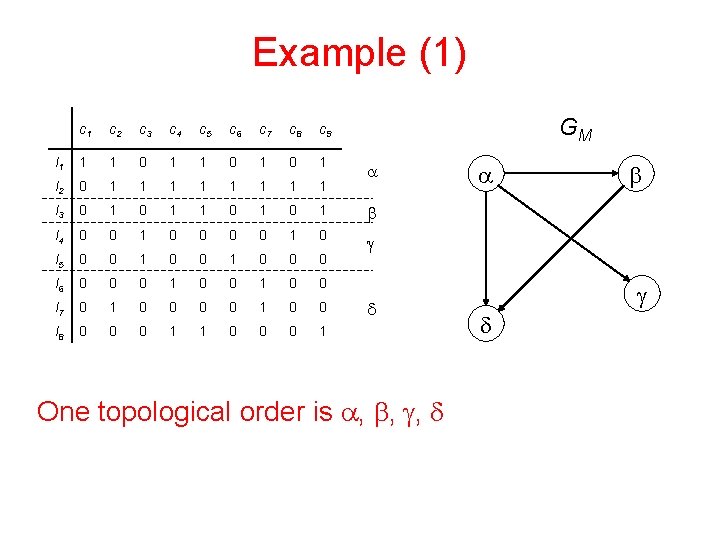
Example (1) GM c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 c 9 l 1 1 1 0 1 0 1 l 2 0 1 1 1 1 l 3 0 1 1 0 1 b l 4 0 0 1 0 l 5 0 0 1 0 0 0 g l 6 0 0 0 1 0 0 l 7 0 1 0 0 l 8 0 0 0 1 1 0 0 0 1 a d One topological order is a, b, g, d a b g d

Example (2) {1} a l 1 l 2 … … {2, 4, 5, 7, 9} 1 0 1 1 {3, 6, 8} 1 1 1 1 1 … {4} {7} {2} 1 1 0 0 1 0 {2, 4, 5, 7, 9} b l 1 … 1 1 {9, 5} d g l 6 l 7 l 8 l 4 l 5 … … … 0 0 1 1 0 1 {6} {3} {8} 0 1 1 0 … … … 0 1 0 1 … …

Example (3) {1} l 1 l 2 l 3 … … … 1 0 0 {2, 4, 5, 7, 9} 1 1 1 {9, 5} l 6 l 7 l 8 … … … 0 0 1 {3, 6, 8} 1 1 1 1 1 {4} {7} {2} 1 0 1 1 1 0 0 1 1 1 … … … 0 1 0 … … …

Example (4) {1} l 1 l 2 l 3 l 6 l 7 l 8 l 4 l 5 … … … … {9, 5} 1 0 0 0 1 1 1 0 0 1 {6} {3} {8} 0 1 1 0 {4} {7} {2} 1 1 1 1 0 … … {3, 6, 8} 0 1 0 0 0 0 0 1 0 0 … … …

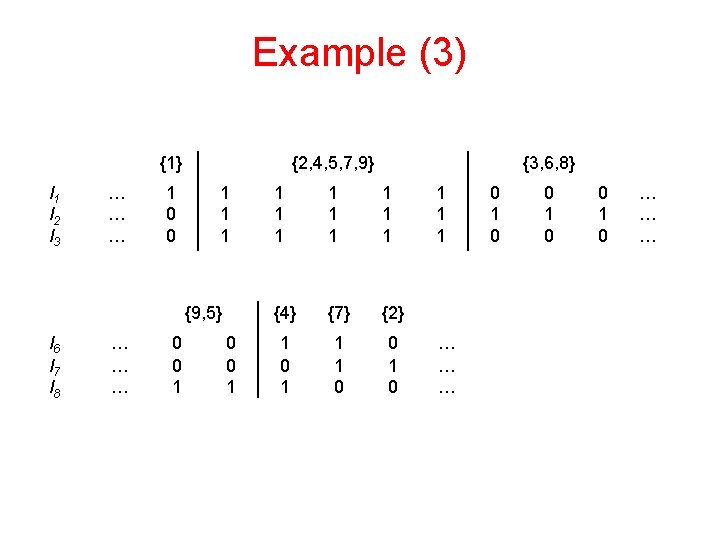
Example (5) {1} {9, 5} {4} {7} {2} {6} {3} {8} l 1 … 1 1 1 0 0 0 … l 2 … 0 1 1 1 1 … l 3 … 0 1 1 1 0 0 0 … l 6 … 0 0 0 1 1 0 0 … l 7 … 0 0 1 1 0 0 0 … l 8 … 0 1 1 1 0 0 0 … l 4 … 0 0 0 0 1 1 … l 5 … 0 0 0 1 1 0 … In this particular case there are two solutions corresponding to the permutation of identical columns (5 and 9)

Algorithm solution is not unique In general multiple solutions may exist because: • Each component may on its own have several solutions • Each solution can be used in two ways: the permutation and its reversal

Algorithm running time Topological sorting of GM takes time O(n+m) If the entries of M are preprocessed the queries needed for traversing GM can take constant time Preprocessing takes at most O(nm) Total time for processing each component ci is O(nim) Algorithm running time is O(nm)

Concluding remarks (1) Even if a C 1 P permutation exists, this is not necessarily the true permutation: • The solution is not unique • In general errors do exist, so the true permutation is not the C 1 P one

Concluding remarks (2) Generalizations to account for errors yield NPhard problems Also relaxing the assumption of unique probes yields NP-hard problems

Related works A considerably more complicated algorithm from Booth and Leuker exists (1976) that takes O(n+m+r) time (r is the total number of 1 s) Quite recently a simple O(n+m+r)-time algorithm has been presented by Hsu - J Algorithms 43 (2002), no. 1, 1 -16