Algoritmos de ordenacin Realizado por Jos Carlos Snchez

Algoritmos de ordenación Realizado por: José Carlos Sánchez Martínez Carlos Zaragoza Inglés 1

Introducción • Ordenación: algoritmo ampliamente utilizado. – En programación paralela: para distribuir datos. • Dos tipos de algoritmos: – Basados en comparación. • Se basan en la operación comparar-intercambiar. • Límite inferior de complejidad: O(n * log n). – No basados en comparación. • Basado en la representación de los números. • Límite inferior de complejidad: O(n). 2

Introducción • En ordenación secuencial los mejores algoritmos son O (n*log n). – Ejemplo: Quicksort, Mergesort. • Con n procesadores, se desea O(log n). • Demostrado por Leighton 84, aunque con una elevada constante oculta en la demostración. 3

Características de la ordenación en paralelo • Distribución de los datos (al principio / al final): – Todos los elementos en el mismo procesador. – Cada procesador contiene un bloque de elementos. • Todos los elementos de Pi son menores que los de Pj si i < j. • Cómo se realizan las comparaciones: – Cada procesador tiene un único elemento. – Cada procesador posee un bloque de elementos. 4

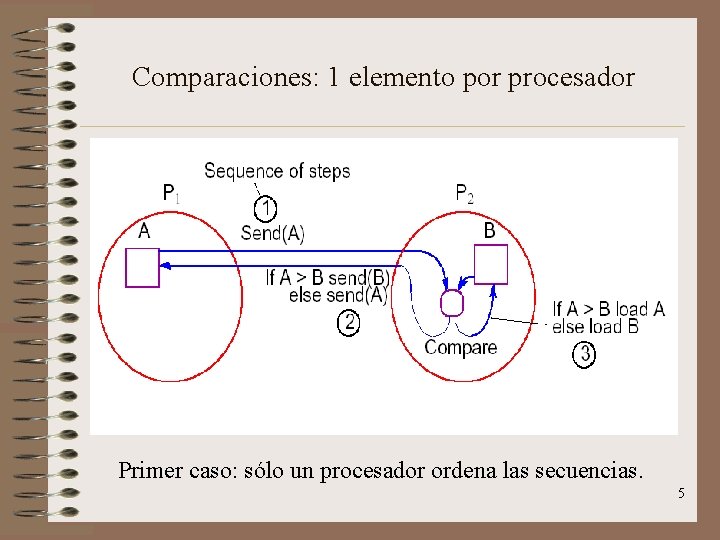
Comparaciones: 1 elemento por procesador Primer caso: sólo un procesador ordena las secuencias. 5

Comparaciones: 1 elemento por procesador Segundo caso: ambos procesadores realizan la ordenación. 6

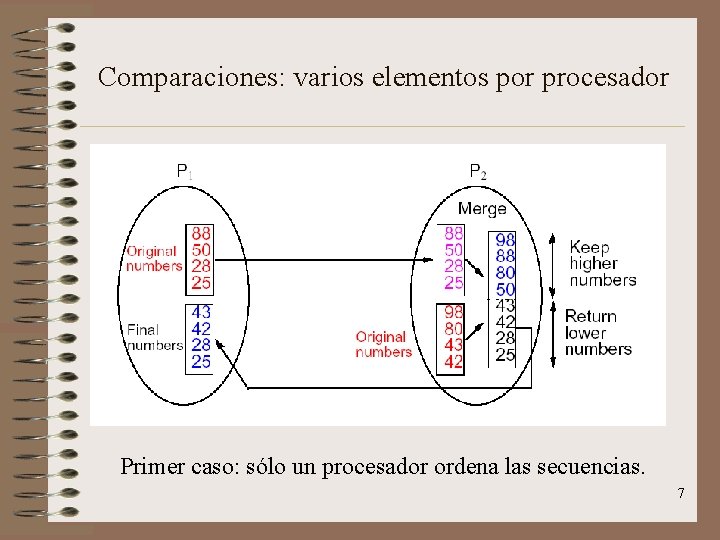
Comparaciones: varios elementos por procesador Primer caso: sólo un procesador ordena las secuencias. 7

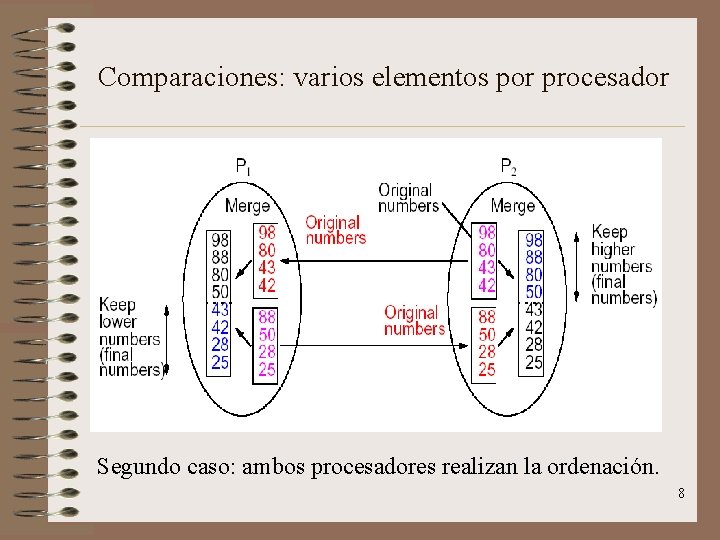
Comparaciones: varios elementos por procesador Segundo caso: ambos procesadores realizan la ordenación. 8

Algoritmos estudiados • • Mergesort Bitonic. Ordenación de la burbuja y variantes. Ordenación por enumeración. Quicksort y variantes. Ordenación por cubetas. Ordenación por muestreo. Ordenación Radix. Ordenación por rangos. 9

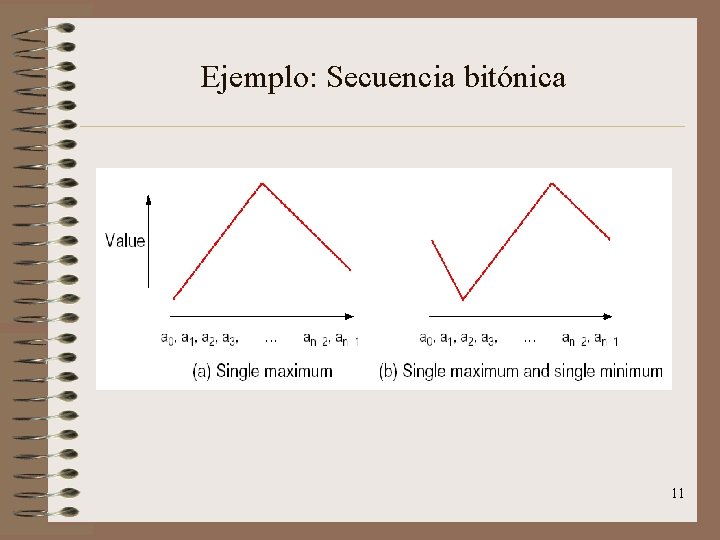
Mergesort Bitonic: Explicación. • Introducido en 1. 968 por Batcher. • Secuencia bitónica: una secuencia de elementos <a 0, a 1, a 2, …, an-1> tal que: 1) O existe un índice i tal que <a 0, a 1, …, ai> es monótonamente creciente y <ai+1, …, an-1> es monótonamente decreciente. 2) O existe un desplazamiento cíclico de los índices tal que 1) se cumpla. 10

Ejemplo: Secuencia bitónica 11

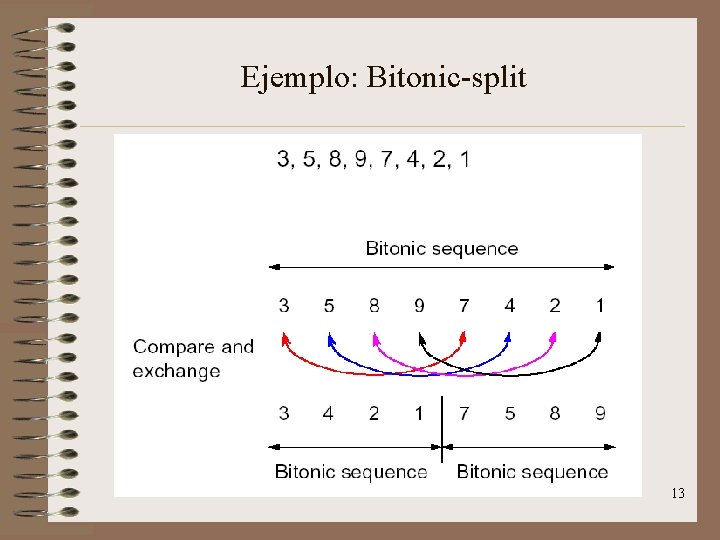
Bitonic-split • Propiedad (de toda secuencia bitónica de n elementos): • Si realizamos la operación “comparar-intercambiar” con los elementos ai y a(i+n/2), obtenemos dos subsecuencias bitónicas, con los números de una secuencia menores que los de la otra. • Aplicando recursivamente “comparar-intercambiar” a las subsecuencias, llegaremos a listas bitónicas de tamaño uno, y así la lista inicial de n elementos estará ordenada. 12

Ejemplo: Bitonic-split 13

Ejemplo: Bitonic-split 14

Pero, ¿y si la secuencia no es bitonic? - Problema: necesitamos que la secuencia de entrada cumpla unas propiedades que normalmente no va a cumplir. - Idea: Para ordenar una secuencia cualquiera tendremos que ordenar con mezclado bitonic secuencias cada vez mayores de elementos. - ¿Por qué funciona esta idea? . - Una secuencia de dos elementos es siempre una secuencia bitonic. - Cualquier secuencia de elementos se puede ver como una concatenación de varias (muchas) secuencias bitonic de 2 elementos. - Al concatenar las partes ascendentes y descendentes de dos secuencias bitonic se obtiene otra secuencia bitonic. 15

Algoritmo • Consideremos el caso en el que cada procesador contiene sólo un elemento de la secuencia a ordenar. • Los procesadores que difieran en el iésimo bit menos significativo realizarán (log n – i + 1) operaciones “compare-exchange”. – Hipercubo (de dimensión d): • En un hipercubo, los procesadores que difieren en un único bit son vecinos. • En el iésimo paso, los procesadores que difieran en el (d-i+1) bit realizarán una operación “compare-exchange”. – Malla: • Conectividad menor que en el hipercubo. • Buscamos que la mayoría (pero no todas) las comparaciones-intercambio se realicen entre vecinos físicos. 16

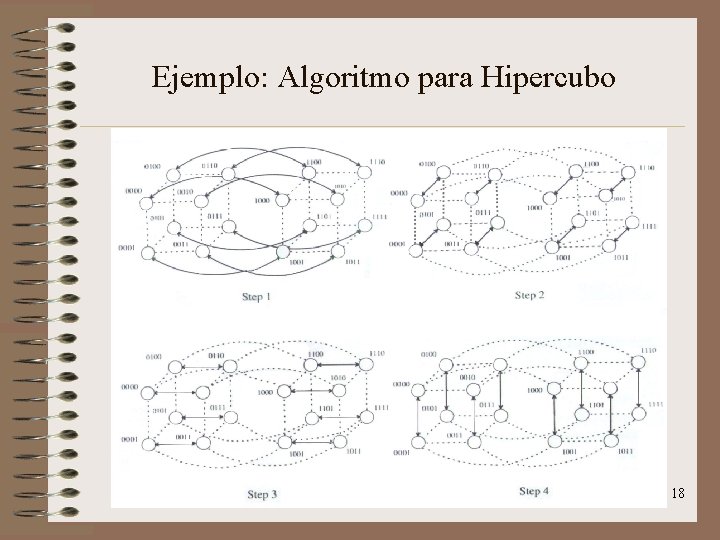
Algoritmo para Hipercubo // label: Etiqueta del procesador = secuencia binaria de “d” bits. // d: número de dimensiones = número de vecinos de cada procesador. // comp_exchange_max(j): compara el elemento local con el elemento del procesador más // cercano a través de la j-ésima dimensión y retener el mayor. PROCEDURE Bitonic_sort(label, d) BEGIN FOR i: =0 TO (d-1) DO FOR j: =i DOWNTO 0 DO IF (nésimo((i+1), label) <> (nésimo(j, label))) comp_exchange_max(j); ELSE comp_exchange_min(j); END; 17

Ejemplo: Algoritmo para Hipercubo 18

Algoritmo para Malla 19

Comparativa Hipercubo-Malla Topología Comparaciones Hipercubo Malla TP O (n * log n) O (log 2 n) + O (√n) No es óptima porque no es O(n * log n), pero si es mejor que la versión secuencial de la ordenación bitonic ya que allí se obtiene O(n * (log n)2). 20

Ordenación de la burbuja • Algoritmo inherentemente secuencial. – (n-1) iteraciones en el peor de los casos. – Orden secuencial O (n 2). • Trabajaremos con variantes de la burbuja: – Transposición impar-par. – Shellsort. 21

Variante: Transposición impar-par • • • Consta de “n” fases. En cada una se hacen O(n) comparaciones. O (n 2). Distingue entre fases “impares” y fases “pares”. – – • Si tenemos un elemento por procesador: – – – • En la fase impar, se comparan (a 1, a 2), (a 3, a 4), …, (an-1, an). En la fase par, se comparan (a 2, a 3), (a 4, a 5), …, (an-2, an-1). En cada fase se hace una comparación con el vecino inmediato O(1). Tiempo de ejecución paralela: O(n). Producto procesador-tiempo O(n 2) Formulación no óptima en coste. Si tenemos más de un elemento por procesador: – – – “p” bloques de (n / p) elementos. Se ordenan de forma local. Se hacen “p” fases: la mitad pares y la mitad impares. En cada fase se hacen O(n / p) comparaciones y O(n / p) comunicaciones. Tp = Orden. Local + Comparac. + Comunic. = O( (n / p) * log (n / p) ) + O(n). Formulación óptima en coste, pero poco escalable. 22

Algoritmo: Transposición impar-par PROCEDURE Impar-Par(n, id) BEGIN FOR i: =1 TO n DO BEGIN IF impar(i) THEN IF impar(id) THEN compare_exchange_min(id+1); ELSE compare_exchange_max(id-1); ELSE IF par(id) THEN compare_exchange_min(id+1); ELSE compare_exchange_max(id-1); END; 23

Ejemplo: Transposición impar-par. 24

Variante: Shellsort • Problema: la tranposición impar-par mueve los elementos paso a paso. – Demasiados movimientos Queremos recorrer distnacias más largas. • Nosotros veremos Shellsort aplicado a un hipercubo. • Supongamos: – – “n”: es el número de elementos a ser ordenados. “p = 2 d”: es el número de procesadores de un hipercubo de d dimensiones. Cada procesador tiene asignados (n / p) elementos. Los procesadores están ordenados según el código Gray. 25

Variante: Shellsort • El algoritmo funciona en 3 fases: – Fase 1: Ordenación local del bloque. O( (n / p) * log ( n / p) ). – Fase 2: Los procesadores más alejados realizan operaciones de comparaciónparticionamiento. • Se hacen d= log p operaciones comparación-particionamiento. • Cada una de ellas requiere O(n / p). – Fase 3: se hacen “l” pasos pares y “l” pasos impares. • Cada paso requiere un tiempo O(n / p). • Tp = O( (n / p) * log (n / p) ) + O( (n / p) * log p ) + O( (l * n) / p ). 26

Ordenación por enumeración • No basado en comparación. • Rango de un elemento ai: número de elementos menores en la secuencia. • Este algoritmo busca calcular el rango de cada elemento. – Para situar cada elemento en la posición correcta de la secuencia ordenada. • Consideraremos este algoritmo dentro de un modelo CRCW RAM. – Asumimos que la escritura concurrente a la misma posición de memoria desemboca en la suma de todos los valores escritos en esa posición. • Consideraremos n 2 procesadores constituyendo una matriz bidimensional. 27

Algoritmo: Ordenación por enumeración • • Se usa un array auxiliar C[1. . n] para almacenar el rango de cada elemento. Funcionamiento en dos pasos: – Primer paso: cada columna j de procesadores calcula el rango de aj. – Segundo paso: cada procesador P 1, j de la primera fila sitúa aj en su posición correcta tal y como es determinado por su rango. • Ordenamos n elementos usando n 2 procesadores en un tiempo O(1). 28

Algoritmo: Ordenación por enumeración PROCEDURE Enumeracion(n) BEGIN FOR EACH processor P 1, j DO C[j]: =0; FOR EACH processor Pi, j DO IF (A[i]<A[j]) OR ((A[i]=A[j]) AND (i<j)) THEN C[j]: =1; ELSE C[j]: =0; FOR EACH processor P 1, j DO A[C[j]]: =A[j]; END; 29

Quicksort • Supongamos una secuencia inicial A[1. . n]. • Funciona en 2 fases: – Fase “divide”: • Se coge una secuencia A[q. . r] • Se descompone en dos secuencias A[q. . s] y A[s+1. . r] donde se cumple que todo elemento de la primera secuencia es menor o igual que cualquier elemento de la segunda. – Para el particionamiento se utiliza un pivote. – Un buen pivote produciría dos subsecuencias de tamaño (k / 2). O(n * log n). – Un mal pivote produciría una subsecuencia de tamaño 1 y otro de tamaño (k-1). O(n 2). – Fase “vencerás”. • Se aplica recursivamente el algoritmo para ordenar cada una de las subsecuencias obtenidas en la fase “divide”. 30

Algoritmo: Quicksort PROCEDURE Quicksort(A, q, r) BEGIN IF (q < r) THEN BEGIN x: =A[q]; s: =q; FOR i: =(q+1) TO r DO IF (A[i]<=x) THEN BEGIN s: =s+1; swap(A[s], A[i]); END; swap(A[q], A[s]); Quicksort(A, q, s); Quicksort(A, s+1, r); END; 31

Paralelizando Quicksort • Veremos 4 formulaciones paralelas distintas: – – Formulación inicial sencilla. Formulación para una CRCW PRAM. Formulación para un hipercubo. Formulación para una malla. 32

Formulación sencilla • Un enfoque paralelizar este algoritmo sería hacer que cada procesador reciba una subsecuencia, la divida en dos trozos y asigne cada trozo a un procesador distinto. • Al principio del algoritmo se le daría toda la secuencia a un único procesador. • Problemas: – Requiere n procesadores para ordenar n elementos. – El tiempo de ejecución es O(n) ya que el particionamiento inicial de los n elementos lo debe hacer un único procesador. – Producto tiempo-procesador es O(n 2). No es óptima. 33

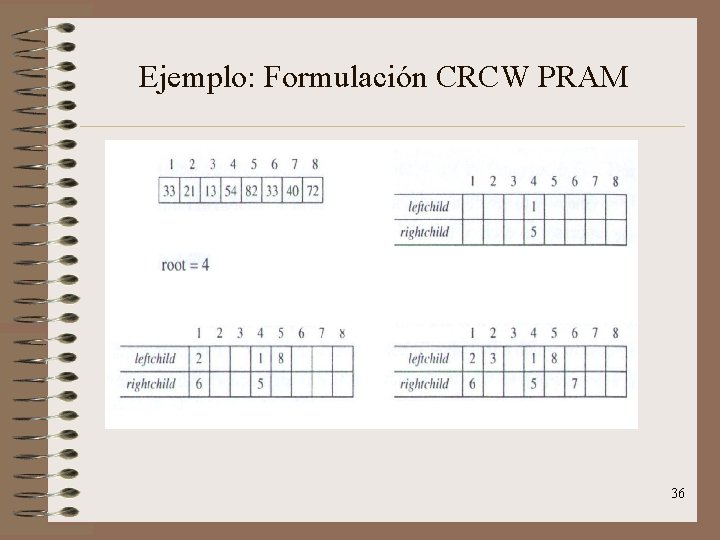
Formulación CRCW PRAM • CRCW PRAM: es una máquina paralela, de acceso aletatorio, con lecturas concurrentes, con escrituras concurrentes y en la que los conflictos (de lectura o escritura) se resuelven aleatoriamente. • Idea: ejecutar quicksort es lo mismo que construir un árbol binario de ordenación en el que la raíz de cada subárbol es un pivote. 34

Algoritmo: Formulación CRCW PRAM PROCEDURE Build_tree(A[1. . n]) BEGIN FOR EACH processor i DO BEGIN root: =i; parenti: =root; // parenti representa al procesador cuyo elemento es el pivote. rightchild[i]: =(n+1); leftchild[i]: =rightchild[i]; END; REPEAT FOR EACH (processor i <> root) DO BEGIN IF ((A[i]<A[parenti]) OR (A[i]=A[parenti] AND i<parenti)) THEN leftchild[parenti]: =i; IF (i=leftchild[parenti]) THEN exit(); ELSE // Sólo un procesador escribirá aquí. // Un procesador para cuando su elemento es // elegido como pivote. ELSE parenti: =leftchild[parenti]; rightchild[parenti]: =i; IF (i=rightchild[parenti]) THEN exit(); // Sólo un procesador escribirá aquí. // Un procesador para cuando su elemento es // elegido como pivote. ELSE parenti: =rightchild[parenti]; END; 35

Ejemplo: Formulación CRCW PRAM 36

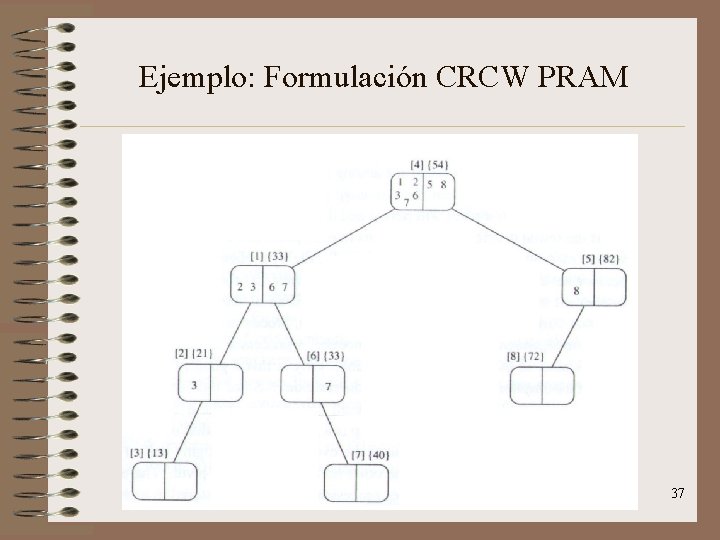
Ejemplo: Formulación CRCW PRAM 37

Análisis: Formulación CRCW PRAM • Todos los pivotes excepto el primero se elijen en paralelo. • La construcción del árbol tiene un orden O(log n) ya que: – – • Después de construir el árbol se debe determinar la posición de cada elemento en el array ordenado. – • En cada paso, se particiona la secuencia en 2 partes (log n) iteraciones. En cada iteración se construye un nivel del árbol en un tiempo O(1). Esto requiere recorrer el árbol y contabilizar, para cada nodo, cuántos elementos tiene en su subárbol izquierdo y cuántos en el subárbol derecho. En una PRAM de n procesadores: – – El tiempo de ejecución promedio del algoritmo es O(log n). El producto tiempo-procesador es O(n * log n), que es óptimo en coste. 38

Formulación para hipercubo • Propiedad: – Un hipercubo de dimensión “d” puede dividirse en 2 hipercubos de dimensión (d 1) donde cada procesador de un subcubo está conectado a otro procesador del otro subcubo. 39

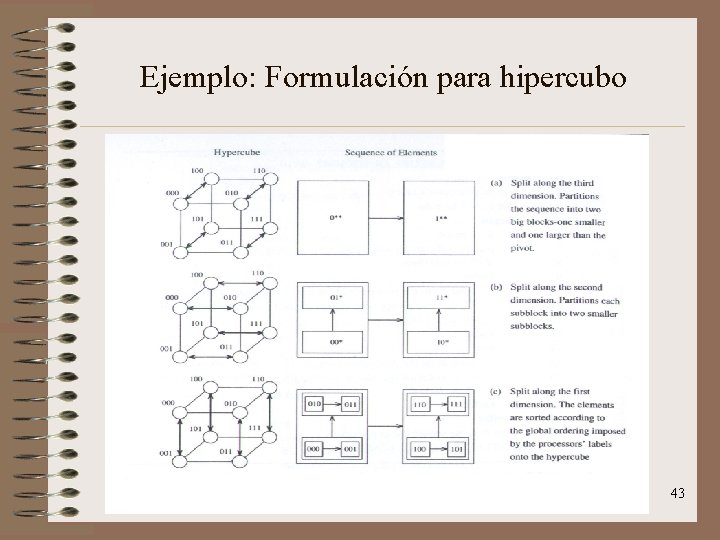
Formulación para hipercubo • Paso del algoritmo: – Elegir un pivote y enviarlo por broadcast a los demás. – Particionar el bloque local usando ese pivote. – Los procesadores conectados a través del d-ésimo enlace intercambian sus bloques de forma que uno de ellos se queda con los elementos menores que el pivote y el otro con los demás. • Resultado del paso: – Después de esto, cada procesador del hipercubo (virtual) de dimensión (d-1) cuyo d-ésimo bit de mayor peso sea cero tendrá los elementos menores que el pivote. – Análogamente, todo procesador del hipercubo (virtual) de dimensión (d-1) cuyo d -ésimo bit de mayor peso sea uno tendrá los elementos mayores que el pivote. 40

Formulación para hipercubo • Este procedimiento se aplica recursivamente en las d dimensiones. – Al final, los elementos están ordenados con respecto al orden impuesto por los procesadores. – Pero los elementos dentro de cada procesador no están ordenados. • Por eso, se aplica entonces una ordenación local por quicksort. 41

Algoritmo: Formulación para hipercubo PROCEDURE Quicksort_hipercubo(B, n, id) BEGIN FOR i: =1 TO d DO BEGIN x: =pivot; particionar(B, x, B 1, B 2); // Tal que se cumple B 1 <= x <= B 2 IF (nesimo_bit(i)=0) Enviar B 2 al procesador a través del iésimo enlace. C: =subsecuencia recibida a través de ese mismo enlace. B: =B 1 U C; ELSE Enviar B 1 al procesador a través del iésimo enlace. C: =subsecuencia recibida a través de ese mismo enlace. B: =B 2 U C; END; 42

Ejemplo: Formulación para hipercubo 43

Análisis de la complejidad • Elegir el pivote: algoritmo de la mediana. – • Tiempo inicial de ordenación local: – • Tiempo 2 = ∑(i=1 hasta d) i = (d * (d + 1)) / 2 = O(log 2 p). Particionar la secuencia: – • Tiempoiésima = O(d – (i – 1)). Broadcast en las (log p) iteraciones: – • Tiempoinicial = O( (n / p) * log (n / p) ). Broadcast de la iésima iteración: – • Tiempo 1 = O(1). Tiempo 3 = O( log (n / p) ) + O ( n / p ). Tiempo de ejecución paralela: – Tp = O ( (n / p) * log (n / p) ) + O( (n / p) * log p ) + O( log 2 p ). 44

Formulación para malla • Los procesadores de la malla están numerados por filas con la numeración ascendente de izquierda a derecha. • El objetivo es ordenar los elementos también en base a ese orden. • La idea del particionamiento recursivo es: – Seleccionar un pivote. – Mover los elementos de forma que al final los elementos menores que el pivote estén en un lado de la malla y los mayores que el pivote estén en el otro lado. 45

Algoritmo: Formulación para malla • Vamos a particionar una secuencia de tamaño k que va desde el procesador Pm hasta el procesador Pm+k. • El proceso consta de 4 pasos: – Se elige un pivote y se envía a Pm. El procesador Pm (que actúa de raíz del árbol) hace un broadcast del pivote. – Cada procesador cuenta el número de elementos menores y mayores que el pivote que hay en sus subárboles y lo propaga hacia arriba en el árbol. • En este punto, el procesador raíz sabe cuántos elementos de la secuencia son menores que el pivote (lo llamaremos “s”) y cuántos mayores (será “k-s-1”). • Por lo tanto, la raíz sabe que el lado izquierdo irá desde la posición m hasta la posición (m + s) y que el lado derecho irá desde laposición (m + s + 1) hasta la posición (m + k). 46

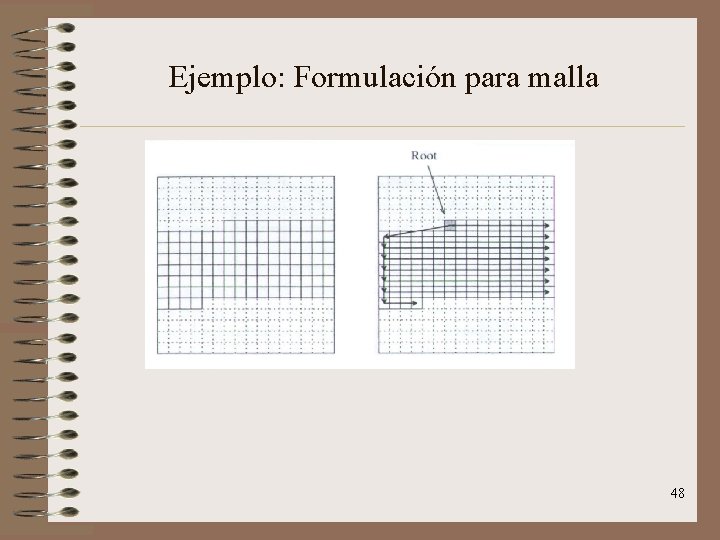
Algoritmo: Formulación para malla – Cada procesador recibe de su padre la siguiente posición vacía en cada una de las dos particiones y elige ponerse en una u otra según le corresponda. – Los procesadores se permutan para situarse en la posición que les corresponda dentro de la secuencia. • Nótese que el objetivo del particionamiento no es ordenar los elementos: es sólo partir la secuencia en dos partes tales que todos los elementos de una parte sean menores que los elementos de la otra. 47

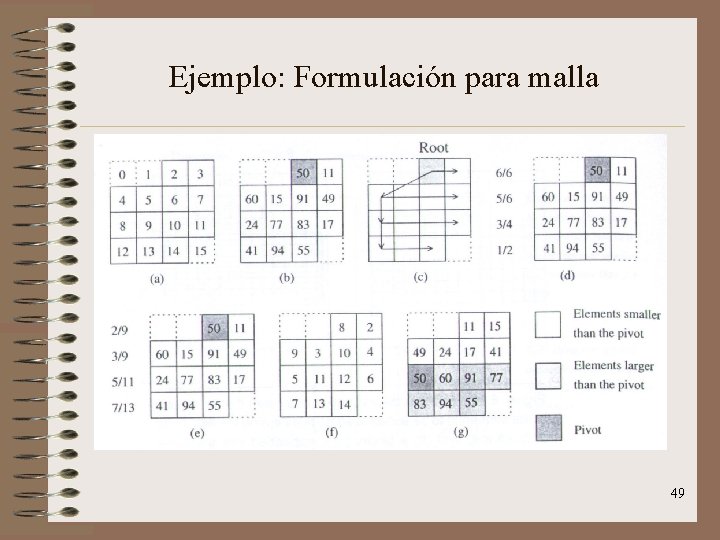
Ejemplo: Formulación para malla 48

Ejemplo: Formulación para malla 49

Análisis de Formulación para malla • El tiempo de ejecución paralela es O(log n * n) ya que: – Asumiendo un buen pivote (log n) iteraciones. – Los pasos 1, 2 y 3 requieren recorrer el árbol. • El camino más largo de la raíz a las hojas es 2 n. • Por lo tanto, este recorrido requiere un tiempo de O( n). – El paso 4 requiere permutar los elementos de la malla. • Esto también requiere un tiempo de O( n). • El producto tiempo-procesador es O(n 1’ 5 * log n). – Esta formulación no es óptima en coste. – De hecho sólo es válida para un número pequeño de procesadores. 50

Algoritmo de cubetas: Paralelización • Cada procesador poseerá un bloque de (n / p) elementos. • Por tanto, habrá p cubetas • Algoritmo: – 1 er paso: cada bloque de (n / p) elementos se divide en p subbloques: uno para cada cubeta. Esto requiere un tiempo de O(n / p) – 2º paso: cada procesador envía los sub-bloques a los apropiados procesadores. Tras esto , cada procesador tiene sólo los elementos que pertenecen a su cubeta. Este paso requiere un tiempo de O(n / p ) + O(p * log p) – 3 er paso: cada procesador ordena su cubeta. Este paso requiere un tiempo de O(n / p). 51

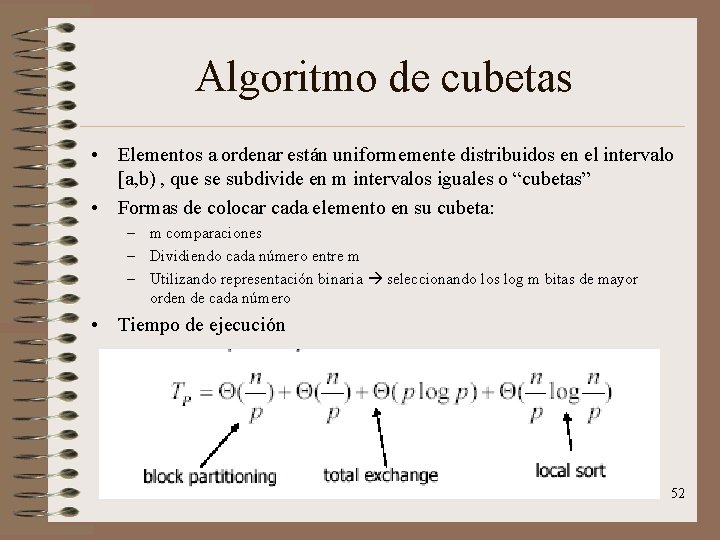
Algoritmo de cubetas • Elementos a ordenar están uniformemente distribuidos en el intervalo [a, b) , que se subdivide en m intervalos iguales o “cubetas” • Formas de colocar cada elemento en su cubeta: – m comparaciones – Dividiendo cada número entre m – Utilizando representación binaria seleccionando los log m bitas de mayor orden de cada número • Tiempo de ejecución 52

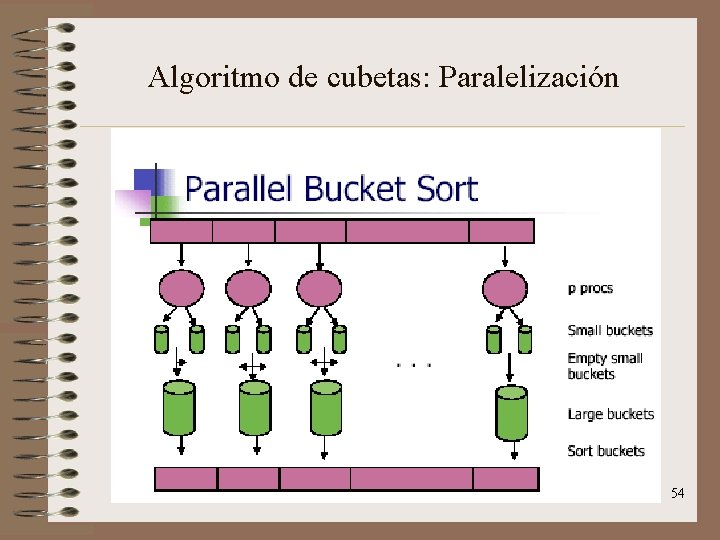
Algoritmo de cubetas: Paralelización • Cada procesador poseerá un bloque de (n / p) elementos. • Por tanto, habrá p cubetas • Algoritmo: – 1 er paso: cada bloque de (n / p) elementos se divide en p subbloques: uno para cada cubeta. Esto requiere un tiempo de O(n / p) – 2º paso: cada procesador envía los sub-bloques a los apropiados procesadores. Tras esto , cada procesador tiene sólo los elementos que pertenecen a su cubeta. Este paso requiere un tiempo de O(n / p ) + O(p * log p) – 3 er paso: cada procesador ordena su cubeta. Este paso requiere un tiempo de O(n / p). 53

Algoritmo de cubetas: Paralelización 54

Ordenación por muestreo • Variación del algoritmo de ordenación por cubetas. • Para elementos no distribuidos uniformemente, la ordenación de cubetas puede llevar a cargas de cubetas muy distintas. • Aquí la idea es que se coge una muestra de tamaño “s”. Y el rango de las cubetas se establece ordenando la muestra y eligiendo (m – 1) elementos de la misma. Estos elementos se llaman splitters y dividen la muestra en m cubetas del mismo tamaño. • A parte de esto, el algoritmo se comporta igual que la ordenación por cubetas. 55

Ordenación por muestreo • Cada procesador ordena sus n/p elementos. • Pi elige p-1 elementos distribuidos de forma uniforme del bloque ordenado. • Pi manda los p-1 elementos a P 0. • P 0 ordena los p*(p-1) elementos y selecciona los p-1 “splitters”. • P 0 envía por broadcast los p-1 splitters a todos los procesos. • El algoritmo continua de forma idéntica al de ordenación por cubetas. 56

Ordenación por muestreo Paso Complejidad Explicación Splitters O( n/P + lg(P) ) n/P Ordenar n/P elementos lg(P) transmitir a nodo inicial Envío a cubetas O(n/P + lg(P) + P + n/P * lg (P )) P leer todos los nodos lg( P ) broadcast n/P * lg ( P ) búsqueda binaria de los splitters n/ P enviar splitters a cada nodo Ordenar cubetas O( n/P ) Ordenar cada cubeta Complejidad total: O( n/P * lg( P ) + P ) 57

Algoritmo Radix • Se basa en la representación en cifras de los números. Sea b el número de cifras en dicha representación. • El algoritmo radix analiza en cada instante sólo r cifras de la representación de un elemento. • Este algoritmo requiere (b / r) iteraciones. Durante la iteración “i”, ordena los elementos en base a esas i cifras más significativos. Si dos bloques tienen la misma i cifra más significativos, mantiene el orden existente entre ellos (se dice que el algoritmo es estable). Tp = (b / r) * 2 r * (O(log n) + O(n)). 58

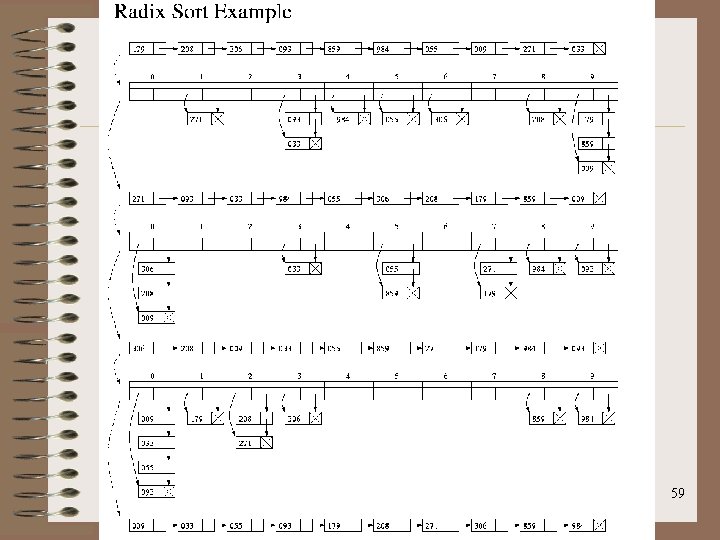
Algoritmo Radix 59

Rank sort: ordenación por rangos • Para cada elemento, se cuenta los menores que él. • Este valor será la posición (el rango o rank) del número seleccionado en la lista • Comparar un número con n-1 números requiere al menos n-1 pasos. Haciendo esto con n números requiere n*(n-1) pasos, y una complejidad de O(n 2) 60

Rank sort: paralelización con n procesadores • Cada procesador sería el encargado de encontrar la posición final de casa número. • Con todos los procesadores trabajando en paralelo la complejidad sería de O (n). Esta complejidad es inferior a cualquier algoritmo de ordenación secuencial, y puede ser mejorada. 61

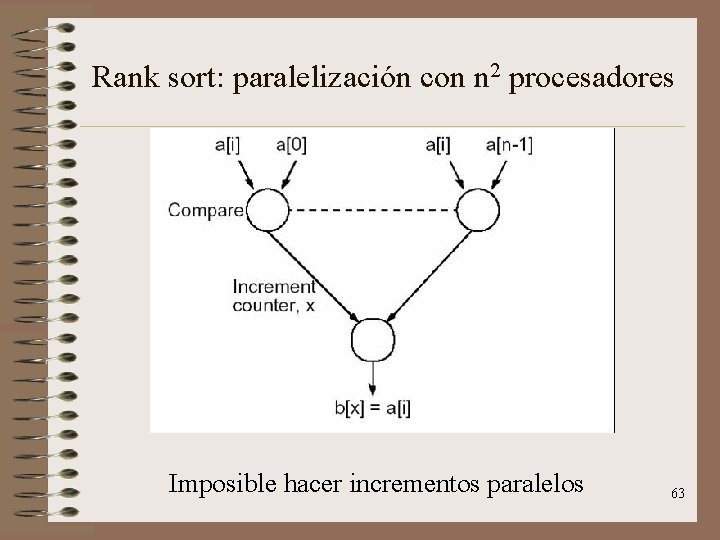
Rank sort: paralelización con n 2 procesadores • La búsqueda de la posición puede ser ejecutada por varios procesadores. • Así n-1 procesadores comparan el número seleccionado con cada uno del resto e incrementaran un contador. • Para ordenador los n números harán falta n(n-1) procesadores. En teoría si todos los incrementos se realizaran de forma paralela la complejidad podría reducirse a O(1). 62

Rank sort: paralelización con n 2 procesadores Imposible hacer incrementos paralelos 63

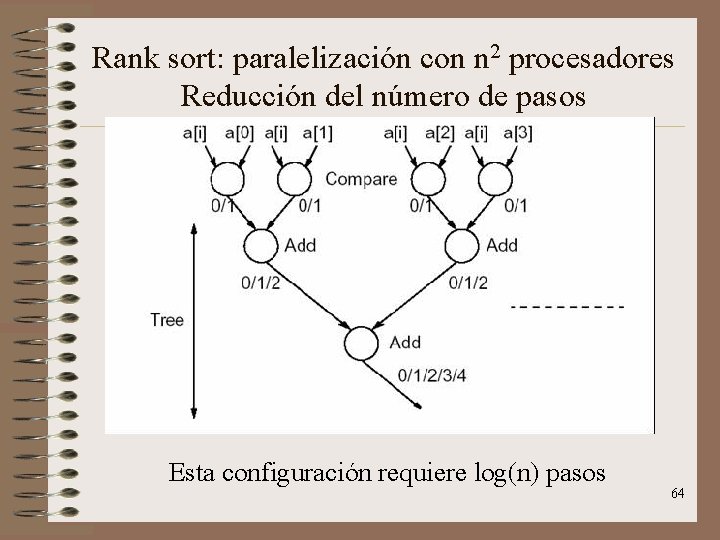
Rank sort: paralelización con n 2 procesadores Reducción del número de pasos Esta configuración requiere log(n) pasos 64

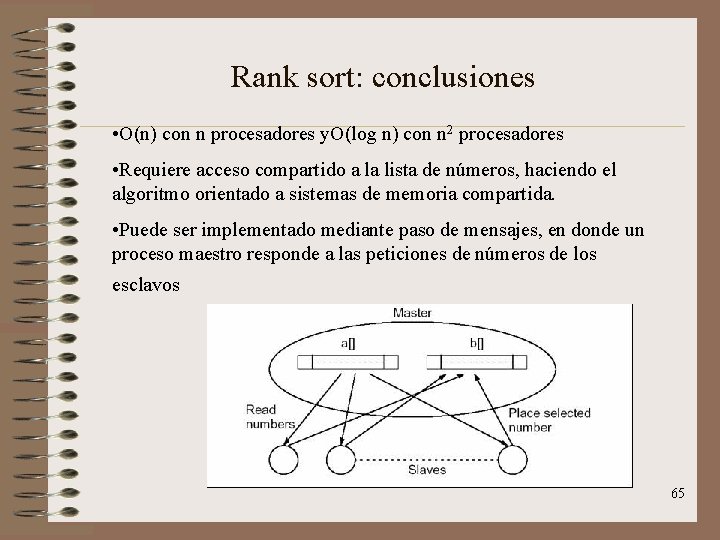
Rank sort: conclusiones • O(n) con n procesadores y. O(log n) con n 2 procesadores • Requiere acceso compartido a la lista de números, haciendo el algoritmo orientado a sistemas de memoria compartida. • Puede ser implementado mediante paso de mensajes, en donde un proceso maestro responde a las peticiones de números de los esclavos 65

Bibliografía • • Capítulo 6 Libro Kumar. Capítulo 9 Libro Wilkinson. • High Performance Computing Archive: – • http: //www. dcs. qmul. ac. uk/SEL-HPC/Articles/Generated. Html/hpc. sort. html Parallel Sorting. CS 442/EECE 443 Introduction to Parallel Computing: – http: //www. cs. unm. edu/~tlw/cs 442. 66