Algoritmos paralelos de grafos y bsqueda pt 1

Algoritmos paralelos de grafos y búsqueda (pt. 1: grafos) Glen Rodríguez Algoritmos paralelos

Agenda n n n n Vista general de las Aplicaciones Definiciones y Representación Árbol recubridor mínimo (Minimum Spanning Tree): Alg. de Prim Ruta más corta (con un solo origen): Dijkstra's Algorithm Todas los pares de Rutas más cortas Clausura transitiva (Transitive Closure) Componentes conectados

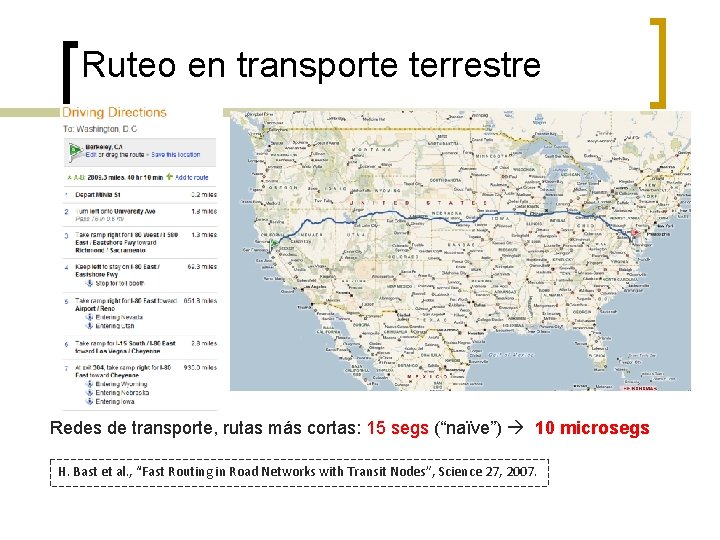
Ruteo en transporte terrestre Redes de transporte, rutas más cortas: 15 segs (“naïve”) 10 microsegs H. Bast et al. , “Fast Routing in Road Networks with Transit Nodes”, Science 27, 2007.

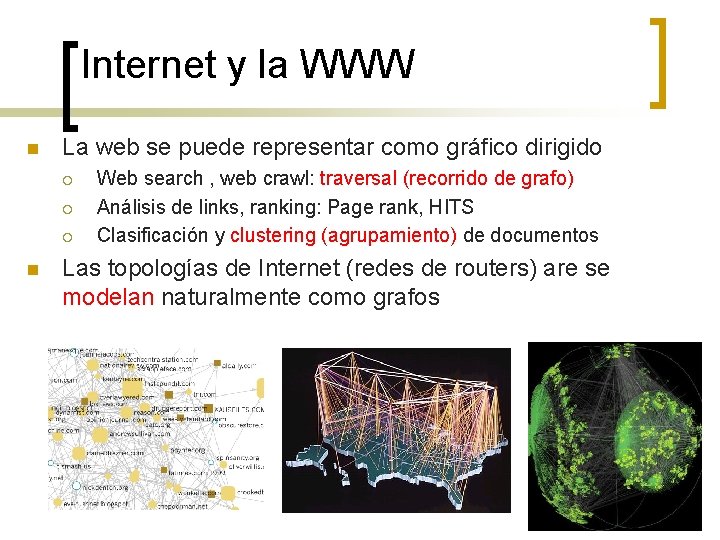
Internet y la WWW n La web se puede representar como gráfico dirigido ¡ ¡ ¡ n Web search , web crawl: traversal (recorrido de grafo) Análisis de links, ranking: Page rank, HITS Clasificación y clustering (agrupamiento) de documentos Las topologías de Internet (redes de routers) are se modelan naturalmente como grafos

Cómputo científico n Reordernar cols/filas en matr. dispersas ¡ Para reducir/concentrar el “lleno” n ¡ n n Diagonal pesada para menos pivoting Estructuras de datos para explotar mejor el patrón disperso Optimización ¡ n Particionar, eigen-vectores Image source: Yifan Hu, “A gallery of large graphs” Matroides, colorear grafos, spanning trees Preconditionadores ¡ ¡ ¡ Factorización incompleta Particionar dominios Grafos en multigrid n ¡ Independent sets, matchings, etc. Teoría de soprte n Spanning trees & graph embedding B. Hendrickson, “Graphs and HPC: Lessons for Future Architectures”, http: //www. er. doe. gov/ascr/ascac/Meetings/Oct 08/Hendrickson%20 ASCAC. pdf Image source: Tim Davis, UF Sparse Matrix Collection.

Análisis de grandes cantidades de data n n n Abstraer algo como grafo es útil parta analizar data con relaciones/estructura complicada. Fuentes de data: simulaciones de peta-escala, sensores en experimentos, Internet, redes de sensores Desafios: enorme tamaño de data, heterogeneidad, incertidumbre, calidad de la data Astrofísica: datasets masivos, variaciones en el tiempo Bioinformática: calidad de data, heterogeneidad Image sources: (1) http: //physics. nmt. edu/images/astro/hst_starfield. jpg (2, 3) www. visual. Complexity. com Redes sociales: anáisis, incertidumbre

Análisis de data y Alg. de grafos en Biología Sistémica n n Estudio de la interacción entre componentes de un sistema biológico Se usan mucho los grafos: ¡ ¡ Predecir nuevas interacciones: modelado Anotación funcional de nuevas proteínas: matching, clustering Identificar rutas metabólicas: rutas, clustering Identificar nuevos complejos de proteínas: clustering, centralidad Image Source: Giot et al. , “A Protein Interaction Map of Drosophila melanogaster”, Science 302, 1722 -1736, 2003.

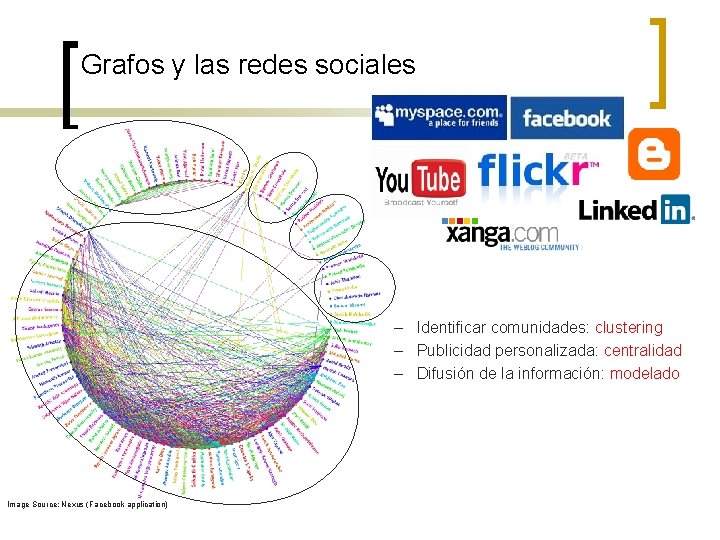
Grafos y las redes sociales – Identificar comunidades: clustering – Publicidad personalizada: centralidad – Difusión de la información: modelado Image Source: Nexus (Facebook application)

Análisis de redes para Inteligencia y Vigilancia n n [Krebs ’ 04] Análisis de redes terroristas usando información pública (luego de Torres Gemelas). Determinar líderes de los patrones de interacción: centralidad Vista globla de las entidades arroja más luces Detectar actividades anormales isomorfismo de subgrafos exacto o aproximado Image Source: http: //www. orgnet. com/hijackers. html Image Source: T. Coffman, S. Greenblatt, S. Marcus, Graph-based technologies for intelligence analysis, CACM, 47 (3, March 2004): pp 45 -47

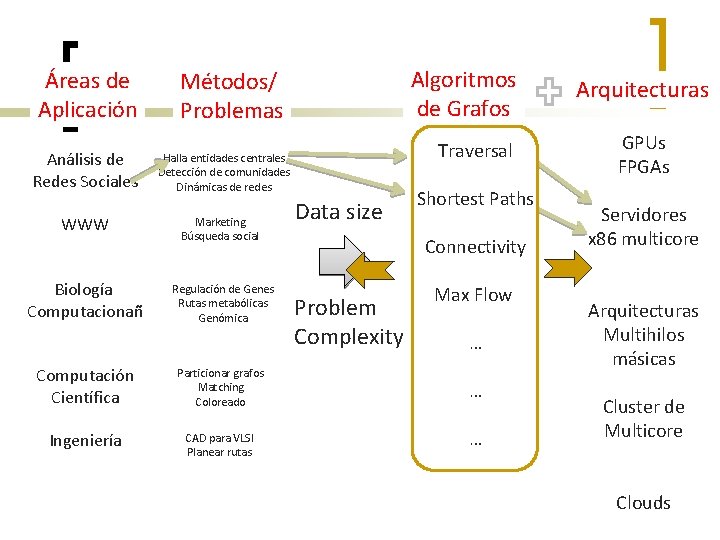
Áreas de Aplicación Análisis de Redes Sociales Algoritmos de Grafos Métodos/ Problemas Traversal Halla entidades centrales Detección de comunidades Dinámicas de redes WWW Marketing Búsqueda social Biología Computacionañ Regulación de Genes Rutas metabólicas Genómica Computación Científica Particionar grafos Matching Coloreado Ingeniería CAD para VLSI Planear rutas Data size Shortest Paths Connectivity Problem Complexity Max Flow … … … Arquitecturas GPUs FPGAs Servidores x 86 multicore Arquitecturas Multihilos másicas Cluster de Multicore Clouds

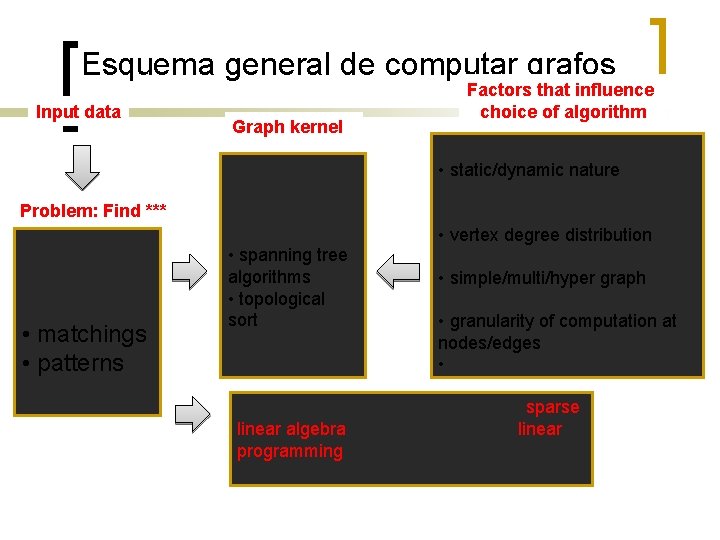
Esquema general de computar grafos Input data Problem: Find *** • paths • clusters • partitions • matchings • patterns • orderings Graph kernel • traversal • shortest path algorithms • flow algorithms • spanning tree algorithms • topological sort …. . Factors that influence choice of algorithm • graph sparsity (m/n ratio) • static/dynamic nature • weighted/unweighted, weight distribution • vertex degree distribution • directed/undirected • simple/multi/hyper graph • problem size • granularity of computation at nodes/edges • domain-specific characteristics Graph problems are often recast as sparse linear algebra (e. g. , partitioning) or linear programming (e. g. , matching) computations

Definiciones y Representación n n Un grafo no dirigido G es un par (V, E), donde V es un cjto. finito de puntos llamados vértices y E es un cjto. finito de aristas o arcos. Una arista e ∈ E es un par no ordenado (u, v), u, v ∈ V. En un grafo dirigido, e es un par ordenado (u, v). Una arista (u, v) es incidente del vértice u y es incidente a v. Una ruta del vértice v al u es una secuencia <v 0, v 1, v 2, …, vk> de vertices donde v 0 = v, vk = u, y (vi, vi+1) ∈ E para i = 0, 1, …, k-1. La longitud de la ruta está definida por el número de aristas en la ruta.

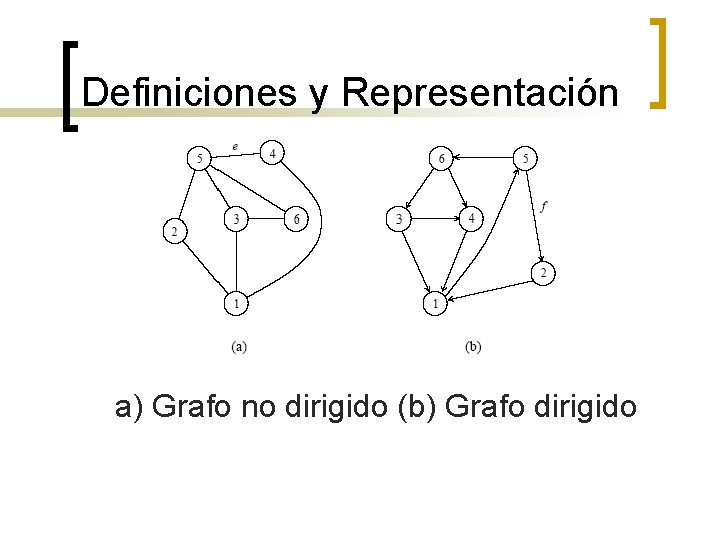
Definiciones y Representación a) Grafo no dirigido (b) Grafo dirigido

Definiciones y Representación n Un grafo no dirigido está conectado si cada par de vértices está conectado por una ruta. Un bosque es un grafo acíclico, y un árbol es un grafo conectado acíclico. Un grafo que tiene pesos asociados con cada arista es un grafo ponderado.

Definiciones y Representación n n Un grafo se puede representar por una matriz de adyacencia o una lista de aristas (o vértices). Las matrices de adyacencia tienen un valor ai, j = 1 si los nodos i , j comparten una arista; 0 en caso contrario. En un grafo ponderado, ai, j = wi, j, el peso de la arista. La lista de adyacencia para un grafo G = (V, E) consiste de un array Adj[1. . |V|] de listas. Cada lista Adj[v] es una lista de todos los vértices adyac. a v. Para un grafo de n nodos, la matriz de adyacencia ocupa espacio de Θ(n 2) y la lista ocupa Θ(|E|).

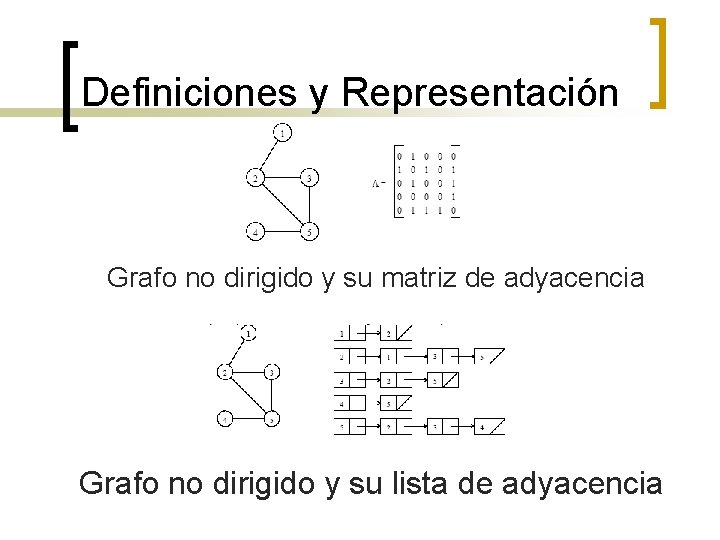
Definiciones y Representación Grafo no dirigido y su matriz de adyacencia Grafo no dirigido y su lista de adyacencia

Minimum Spanning Tree n n n Un spanning tree de un grafo no dirigido G es un subgrafo de G que es un árbol que contiene todos los vértices de G. Un un grafo ponderado, el peso de un subgrafo es la suma de los pesos de las aristas del subgrafo. Un minimum spanning tree (MST) sería el spanning tree con peso mínimo.

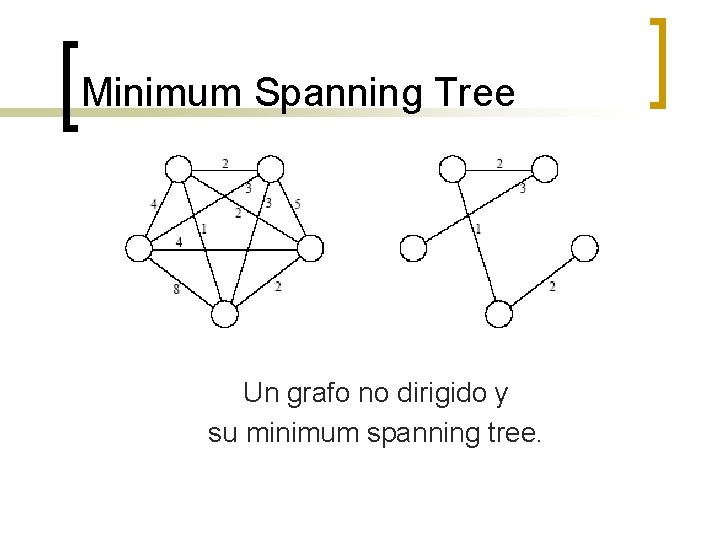
Minimum Spanning Tree Un grafo no dirigido y su minimum spanning tree.

Minimum Spanning Tree: Algoritmo de Prim n n n Es un algoritmo goloso (greedy). Empieza escogiendo un vértice arbitrario, y lo incluye en el actual MST. Hace crecer al actual MST incorporando en él al vértice más cercano a uno de los vértices del actual MST.

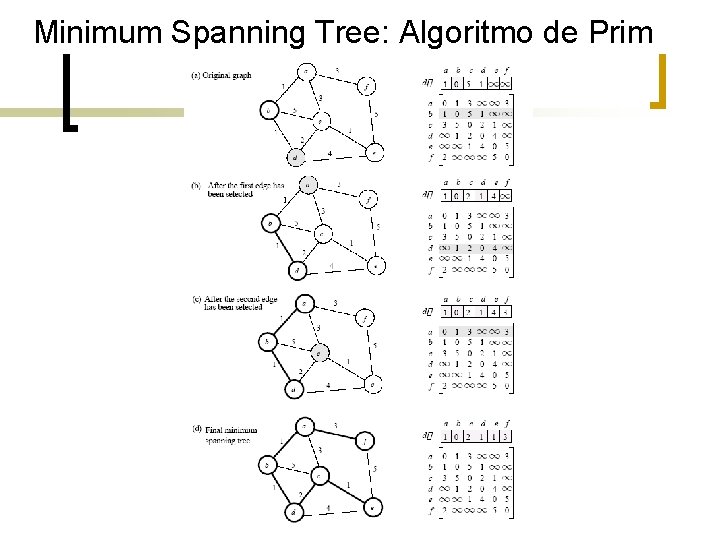
Minimum Spanning Tree: Algoritmo de Prim

Minimum Spanning Tree: Algoritmo de Prim Versión secuencial (no paralela)

Algoritmo de Prim paralelo n n n El “while”– es difícil ejecutarlos en paralelo. El “for” interno es más fácil de paralelizar. Sea p el número de procs. , y n el número de vértices. La matriz de adyacencia se particiona en bloques 1 -D, con el vector de distancia d particionado así también. En cada paso, el proc. escoge el nodo más cerca localmente, luego se hace una reducción global para escoger el nodo más cercano global. Se inserta ese nodo al MST, y se hace el broadcast respectivo a todos los procs. Cada proc. actualiza su parte del vector d localmente.

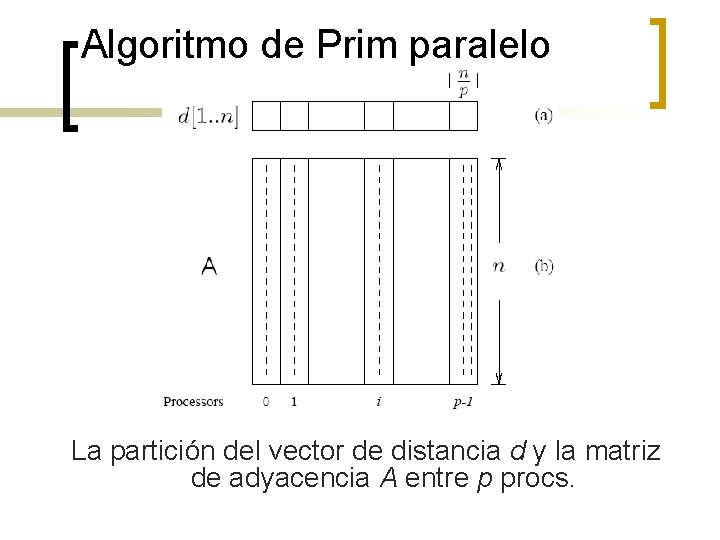
Algoritmo de Prim paralelo La partición del vector de distancia d y la matriz de adyacencia A entre p procs.

Algoritmo de Prim paralelo n n n El costo de seleccionar el nodo más cercano es O(n/p + log p). El costo del broadcast es O(log p). El costo de actualización local del vector d es O(n/p). El tiempo paralelo por iteración es O(n/p + log p). El tiempo total paralelo es O(n 2/p + n log p). La isoeficiencia es O(p 2 log 2 p).

Ruta más corta – un solo origen n En un grafo ponderado G = (V, E, w), el problema de la ruta más corta con un solo origen es encontrar las rutas más cortas de un vértice v ∈ V a los demás vértices en V. El algoritmo de Dijkstra es parecido al de Prim. Mantiene un conjunto de nodos de los cuáles se sabe sus rutas más cortas. Este conjunto crece basado en el nodo más cercano al origen usando uno de los nodos en el actual conjunto de ruta más corta.

Algoritmo de Dijkstra, secuencial

Algoritmo de Dijkstra paralelo n n n Similar a Prim paralelo para MST. La matriz de adyacencia ponderada se particiona usando bloques 1 -D. Cada proceso escoge, localmente, el nodo más cercano al origen, seguido por una reducción global para escoger el siguiente nodo. Se hace broadcast de ese nodo y del vector l actualizado a todos los procesadores Performance paralela es idéntica al Prim paralelo

Rutas más cortas - todos los pares n n Dado un grafo ponderado G(V, E, w), el problema de todos los pares de rutas más cortas es encontrar las rutas más cortas entre todos los pares de vértices vi, vj ∈ V. Hay varios algoritmos que resuelven este problema.

Rutas más cortas - todos los pares: Algoritmo basado en Mat. Mult n n n Considere la multiplicación de la matriz de adyacencia ponderada consigo misma – pero reemplaze las multiplicaciones de números x*y por sumas x+y, y las sumas x+y por min(x, y). El “producto” de la matriz de adyacencia ponderada consigo misma = una matriz que contiene las rutas más cortas de longitud 2 entre cualquier par de nodos. Luego, “ An ” contiene todas las rutas más cortas.

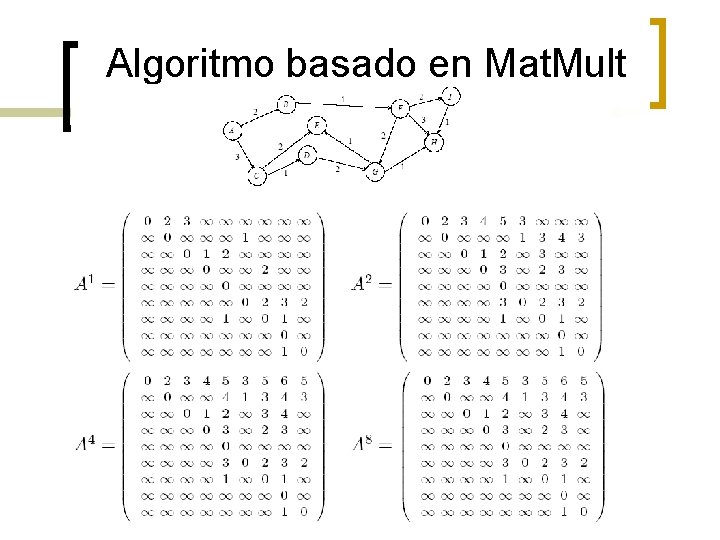
Algoritmo basado en Mat. Mult

Algoritmo basado en Mat. Mult n n “An” es calculado doblando las potencias: A, A 2, A 4, A 8, … Se necesita log n Mat. Mults, cada una se tarda O(n 3). Complejidad serial: O(n 3 log n). Hay mejores algoritmos, con complejidad O(n 3).

Algoritmo basado en Mat. Mult, en paralelo n n n Cada una de las log n Mat. Mults se pueden hacer en paralelo. Se pueden usar n 3/log n procs para computar cada producto matriz-matriz en tiempo log n. Tiempo total: O(log 2 n).

Dijkstra para todos los pares n n Ejecutar n instancias de Dijkstra para 1 solo origen, uno para cada uno de los n vértices como origen. Complejidad es O(n 3).

Dijkstra para todos los pares, en paralelo n Hay dos estrategias paralelizar – ejecutar cada uno de los n problemas de ruta más corta con un solo origen en un diferente procs. (partición de los orígenes), o usar la versión paralela de la ruta más corta con un solo origen (paralelizar cada origen).

Partición de los orígenes n n Use n procs, cada proc Pi calcula las rutas más cortas desde el vértice vi a los demás vertices con Dijkstra secuencial. No hay comunicación entre procesadores (suponiendo que la matriz de adyacencia esta replicada en todos los procs). Tiempo paralelo: Θ(n 2). Es de costo óptimo, pero solo puede usarse n procs. La isoeficiencia es p 3.

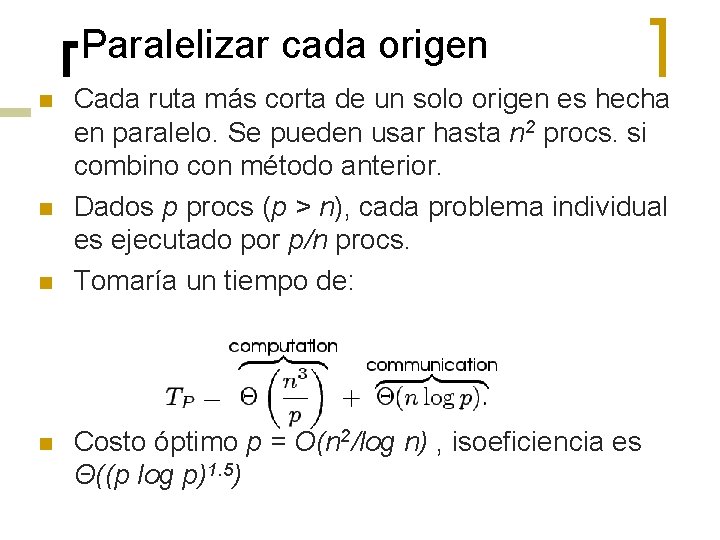
Paralelizar cada origen n n Cada ruta más corta de un solo origen es hecha en paralelo. Se pueden usar hasta n 2 procs. si combino con método anterior. Dados p procs (p > n), cada problema individual es ejecutado por p/n procs. Tomaría un tiempo de: Costo óptimo p = O(n 2/log n) , isoeficiencia es Θ((p log p)1. 5)

Algoritmo de Floyd n n n Para cada par de vértices vi, vj ∈ V, considere todas las rutas de vi a vj cuyos vértices intermedios pertenecen a {v 1, v 2, …, vk}. Sea pi(, kj) (de peso di(, kj) ) la ruta más corta de entre ellas. Si vk está en la ruta más corta de vi a vj, entonces pi(, kj) es la misma que pi(, kj-1) Si vk está en pi(, kj), entonces podemos partir a pi(, kj) en 2 rutas – una de vi a vk y otra de vk a vj. Cada una de estas rutas usan vértices de {v 1, v 2, …, vk-1}.

Algoritmo de Floyd La siguiente relación de recurrencia se observa: Esta ecuación debe ser computada por cada par de nodos y para k = 1, …, n. Complejidad serial es de O(n 3).

Algoritmo de Floyd Computa todas las rutas más cortas entre todos los pares de vértices del grafo G = (V, E) con matriz de adyacencia A.

Algoritmo de Floyd en paralelo con Bloques 2 -D n n n Matriz D(k) se divide en p bloques de tamaño (n / √p) x (n / √p). Cada proc. actualiza su parte de la matriz durante cada iteración. Para computar dl(, kk-1) el proc Pi, j debe obtener dl(, kk -1) and d ( k -1). k, r En general, durante la iteración kesima, cada uno de los √p procs conteniendo parte de la fila kesima la envía a los √p - 1 procs de la misma columna. De la misma forma, cada uno de los √p procs que contienen parte de la kesima columna la envían a los √p - 1 procs de la misma fila.

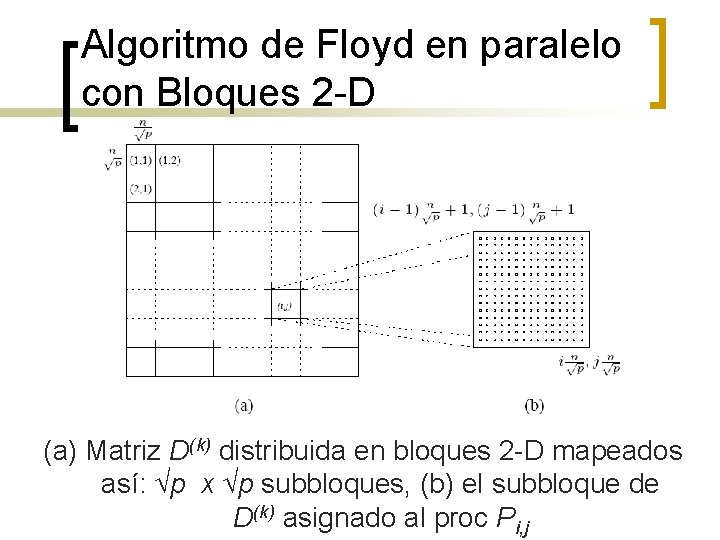
Algoritmo de Floyd en paralelo con Bloques 2 -D (a) Matriz D(k) distribuida en bloques 2 -D mapeados así: √p x √p subbloques, (b) el subbloque de D(k) asignado al proc Pi, j

Algoritmo de Floyd en paralelo con Bloques 2 -D (a) Patrones de comunicación en mapeo en bloques 2 -D. Al computar di(, kj), info debe mandarse a los procs subrayados desde otros 2 procs en la misma fila y columna. (b) La fila y columna de √p procs que contiene la kesima fila y columna las envía junto con columnas y filas.

Algoritmo de Floyd en paralelo con Bloques 2 -D Floyd en paralelo usando blqoues 2 -D. P*, j son todos los procs en la jesima columna, y Pi, * son todos los procs en la fila iesima. La matriz D(0) es la matrix de adyacencia

Algoritmo de Floyd en paralelo con Bloques 2 -D n n n Durante cada iteración del algoritmo, la fila kesima y la columna kesima de procs hacen un broadcast 1 -a-todos a lo largo de sus filas/columnas. El tamaño del broadcast es n/√p elementos, tiempo: Θ((n log p)/ √p). El paso de sincronizar toma Θ(log p). El tiempo de computación es Θ(n 2/p). Tiempo paralelo de Floyd con bloques 2 D es:

Algoritmo de Floyd en paralelo con Bloques 2 -D n n n Se puede usar O(n 2 / log 2 n) procs a costo óptimo. Isoeficiencia es Θ(p 1. 5 log 3 p). Se puede mejorar si se relaja la sincronización estricta luego de cada iteración.

Floyd acelerado con Pipelining n n El paso de sincronización del Floyd paralelo se puede remover sina afectar los resultados. Un proc comienza a trabajar en la kth iteración apenas se ha computado la iteración (k-1)esima y tiene partes relevantes de la matriz D(k-1)

Floyd acelerado con Pipelining Asume que elproc 4 en el tiempo t acaba de computar de la columna kesima de la matriz D(k-1). Manda el segmento a procs 3 y 5. Estos procs reciben el segmento en el momento t + 1 (1 tiempo= lo que tarda un segmento de un nodo a su vecino inmediato). Procs lejos del 4 reciben el segmento después. Proc 1 (en el boundary) no reenvía elemento después de recibirlo.

Floyd acelerado con Pipelining n n n n En cada paso, n/√p elementos de la 1 ra fila se envían desde Pi, j al Pi+1, j. Similarmente, elementos de la 1 ra columna se envían de Pi, j al Pi, j+1. Cada paso demora: Θ(n/√p). Luego de Θ(√p) pasos, el proc P√p , √p obtiene los elementos relevantes de la 1 ra cola y 1 ra col en tpo Θ(n). Los valores de otras filas y cols siguen luego de Θ(n 2/p) modo pipeline. Proc P√p , √p termina su parte de computación en Θ(n 3/p) + Θ(n). Cuando el proc P√p , √p ha terminado en la iteración (n-1)th, envía los valores relevantes de la nth fila y columna a otros procs.

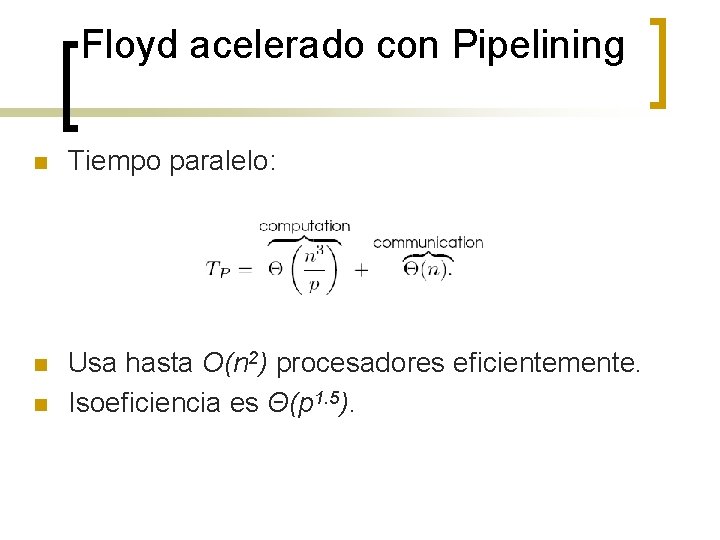
Floyd acelerado con Pipelining n Tiempo paralelo: n Usa hasta O(n 2) procesadores eficientemente. Isoeficiencia es Θ(p 1. 5). n

Comparación n La performance y escalabilidad de varios algoritmos se muestra.

Clausura transitiva (Transitive Closure) n n n Si G = (V, E) es un grafo, entonces la transitive closure de G es el grafo G* = (V, E*), donde E* = {(vi, vj) | hay un path del vi al vj en G} La matriz de conectividad G es una matriz A* = (ai*, j) tal que ai*, j = 1 si hay alguna ruta de vi a vj a i = j, y ai*, j = ∞ de otra manera. Para computar A* se asigna un peso de 1 para cada arista E y se usa cualquiera de las rutas mas cortas - todos los pares.

Componentes conectados n Los componentes conectados de un gafo no dirigido son las clases equivalentes de vértices bajo la relación “es alcanzable desde” Grafo con 3 componentes conectados: {1, 2, 3, 4}, {5, 6, 7}, y {8, 9}.

Usando alg. Depth-First Search n Hacer DFS en el grafo para obtener un bosquecada árbol de la forest es un “connected component” separado (b) Es un bosque obtenido de un trasverse DF del gráfico en (a).

Componentes conectados en paralelo n n Particionar el grafo entre los procs y correr algoritmos independientes en cada proc. En este punto, tenemos p “spanning forests”. En el segundo paso, se combinan estas “forest” de 2 en 2 hasta que solo quede 1.

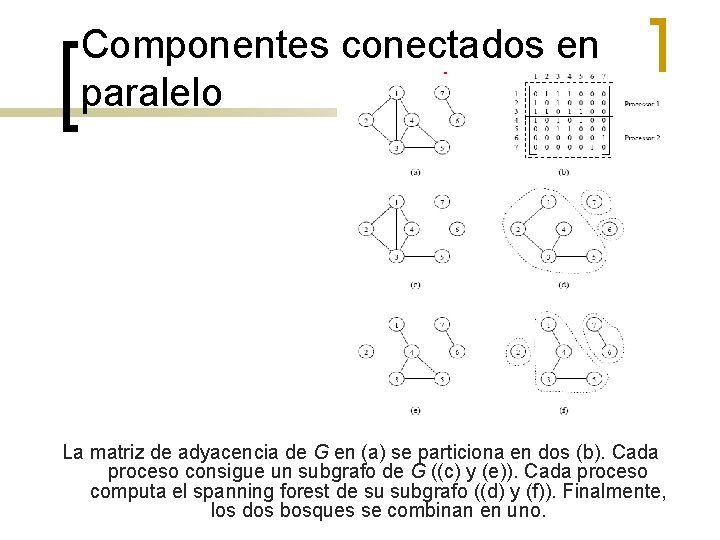
Componentes conectados en paralelo La matriz de adyacencia de G en (a) se particiona en dos (b). Cada proceso consigue un subgrafo de G ((c) y (e)). Cada proceso computa el spanning forest de su subgrafo ((d) y (f)). Finalmente, los dos bosques se combinan en uno.

Componentes conectados en paralelo n n n Para unir pares de bosques, el algoritmo usa conjuntos disjuntos de aristas. Definimos estas operaciones en esos conjuntos: find(x) ¡ n Devuelve un puntero al elemento representativo del cjto conteniendo x. Cada cjto tiene su propio y único representativo. union(x, y) ¡ Une los conjuntos conteniendo los elementos x , y. se asume que los dos cjtos eran disjuntos antes de esta operación.

Componentes conectados en paralelo n n Para unir el bosque A con el B, para cada arista (u, v) de A, se efectúa una operación find para determinar si los vértices están en el mismo árbol de B. Si no, los dos árboles (cjtos) de B conteniendo u y v se unen con una operación unión. Caso contrario, no se hace “union”. Por lo tanto, unir A y B requiere no más de 2(n-1) “find” y (n-1) “union”.

Componentes conectados: paralelo con Bloques 1 -D n n La matriz de adyacencia de tamaño n x n es particionada en p bloques. Cada proc puede computar su “spanning forest” en tiempo Θ(n 2/p). Merging se hace incrustando un árbol logico en la topología. Hay log p etapas del merging, c/u. tarda Θ(n). el costo del merging es Θ(n log p). En cada etapa, los “spanning forests” se envían entre vecinos. Ojo, se transmiten Θ(n) aristas de los “spanning forest”.

Componentes conectados: paralelo con Bloques 1 -D n Tiempo en paralelo: n Para costo óptimo tengo p = O(n / log n). La isoeficiencia es Θ(p 2 log 2 p).