1 Sequential Machine Theory Prof K J Hintz

1 Sequential Machine Theory Prof. K. J. Hintz Department of Electrical and Computer Engineering Lecture 1 http: //cpe. gmu. edu/~khintz Adaptation to this class and additional comments by Marek Perkowski

2 Why Sequential Machine Theory (SMT)? • Sequential Machine Theory – SMT • Some Things Cannot be Parallelized • Theory Leads to New Ways of Doing Things, has also practical applications in software and hardware (compiler design, controllers design, etc. ) • Understand Fundamental FSM Limits • Minimize FSM Complexity and Size • Find the “Essence” of a Machine, – what does it mean that there is a machine for certain task?

3 Why Sequential Machine Theory? • Discuss FSM properties that are unencumbered by Implementation Issues: – Software – Hardware – FPGA/ASIC/Memory, etc. • Technology is Changing Rapidly, the core of theory remains forever. • Theory is a Framework within which to Understand Integrate Practical Considerations

4 Hardware/Software • There Is an Equivalence Relation Between Hardware and Software – Anything that can be done in one can be done in the other…perhaps faster/slower – System design now done in hardware description languages (VHDL, Verilog, higher) without regard for realization method • Hardware/software/split decision deferred until later stage in design

5 Hardware/Software • Hardware/Software equivalence extends to formal languages – Different classes of computational machines are related to different classes of formal languages – Finite State Machines (FSM) can be equivalently represented by one class of languages

6 Formal Languages • Unambiguous • Can Be Finite or Infinite – Give some simple examples • Can Be Rule-based or Enumerated • Various Classes With Different Properties

7 Finite State Machines • FSMs are Equivalent to One Class of Languages • Prototypical Sequence Controller – Generator – acceptor – controller • Many Processes Have Temporal Dependencies and Cannot Be Parallelized, – the need some form of state machine. • FSM Costs – Hardware: More States More Hardware – Time: More States, Slower Operation – Technology dependent: how many CPLD chips?

8 Goal of this set of lectures • Develop understanding of Hardware/Software/Language Equivalence • Understand Properties of FSM • Develop Ability to Convert FSM Specification Into Set-theoretic Formulation • Develop Ability to Partition Large Machine Into Greatest Number of Smallest Machines – This reduction is unique

9 Machine/Mathematics Hierarchy • AI Theory Intelligent Machines • Computer Theory Computer Design • Automata Theory Finite State Machine • Boolean Algebra Combinational Logic

10 Combinational Logic • Feedforward • Output Is Only a Function of Input • No Feedback – No memory – No temporal dependency • Two-Valued Function Minimization Techniques – Well-known Minimization Techniques • Multi-valued Function Minimization – Well-known Heuristics

11 Finite State Machine • Feedback • Behavior Depends Both on Present State and Present Input • State Minimization – Well-known – With Guaranteed Minimum • Realization Minimization – Unsolved problem of Digital Design – Technology related, combinational design related

12 Computer Design: Turing Machines • Defined by Turing Computability – Can compute anything that is “computable” – Some things are not computable • Assumed Infinite Memory • State Dependent Behavior • Elements: – – Control Unit is specified and implemented as FSM Tape infinite Head movements • Show example of a very simple Turing machine now: x--> x+1

13 Intelligent Machines • Some machines display an ability to learn – How a machine can learn? • Some problems are possibly not computable – What problems? – Why not computable? – Something must be infinite?

Automata, aka FSM 14 • Concepts of Machines: – Mechanical • Counters, adders – Computer programs – Political • Towns, highways, social groups, parties, etc – Biological • Tissues, cells, genetic, neural, societies – Abstract mathematical • Functions, relations, graphs Yo abl u sho uld con e to cep b u ts i se FS e like n oth M rob er ar otic eas s

15 FSM - Abstract mathematical concept of many types of behavior • Discrete – Continuous system can be discretized to any degree of resolution • Finite State: – finite alphabets for inputs, outputs and states. • Input/Output – Some cause, some result

16 Set Theoretic Formulation of Finite State Machine • S: Finite set of possible states • I: Finite set of possible inputs • O: Finite set of possible outputs • : Rule defining state change • : Rule determining outputs

17 Types of FSMs • Moore FSM – Output is a function of state only • Mealy FSM – Output is a function of both the present state and the present input Discuss timing differences, show examples and diagrams, discuss fast signaling and PLD realization

18 Types of FSMs • Finite State Acceptors, Language Recognizers – Start in a single, specified state – End in particular state(s) • Pushdown Automata – Not an FSM – Assumed infinite stack with access only to topmost element

19 Computer • Turing Machine – Assumed infinite read/write tape – FSM controls read/write/tape motion – Definition of computable function – Universal Turing Machine reads FSM behavior from tape

Review of Set Theory 20 • Element: “a”, a single object with no special property • Set: “A”, a collection of elements, i. e. , – Enumerated Set: – Finite Set:

21 Sets – Infinite set – Set of sets

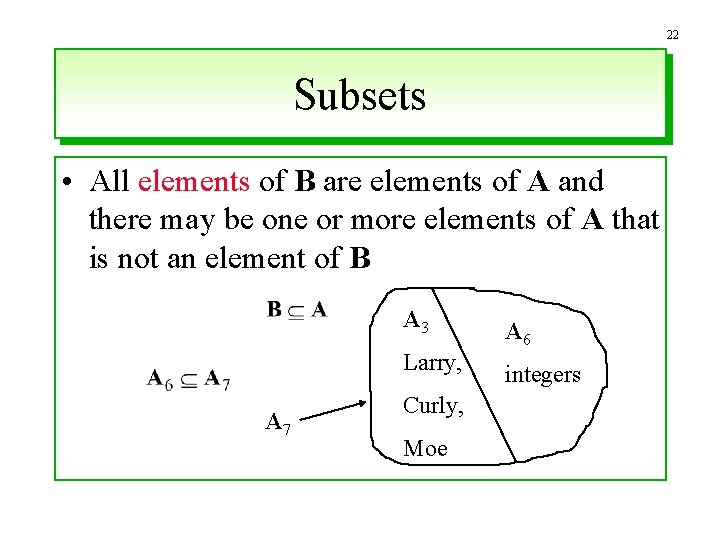
22 Subsets • All elements of B are elements of A and there may be one or more elements of A that is not an element of B A 7 A 3 A 6 Larry, integers Curly, Moe

23 Proper Subset • All elements of B are elements of A and there is at least one element of A that is not an element of B

24 Set Equality • Set A is equal to set B

25 Sets • Null Set – A set with no elements, • Every set is a subset of itself • Every set contains the null set

26 Operations on Sets • Intersection • Union Logical AND Logical OR

27 Operations on Sets • Set Difference • Cartesian Product, Direct Product

28 Special Sets • Powerset: set of all subsets of A *no braces around the null set since the symbol represents the set

29 Special Sets • Disjoint sets: A and B are disjoint if • Cover: We know set covering problem from 572. It was defined as a matrix problem

30 Properties of Operations on Sets • Commutative, Abelian • Associative • Distributive Left hand distributive

31 Partition of a Set • Properties • pi are called “pi-blocks” or “ -blocks” of PI

32 Relations Between Sets • If A and B are sets, then the relation from A to B, is a subset of the Cartesian product of A and B, i. e. , • R-related:

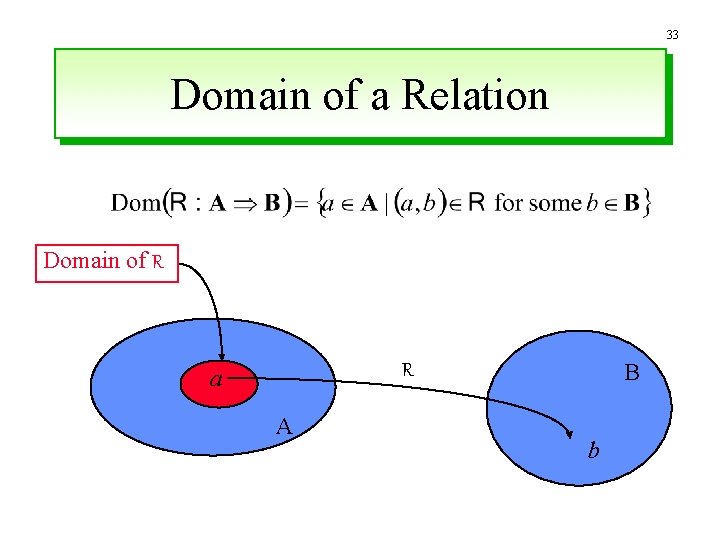
33 Domain of a Relation Domain of R B R a A b

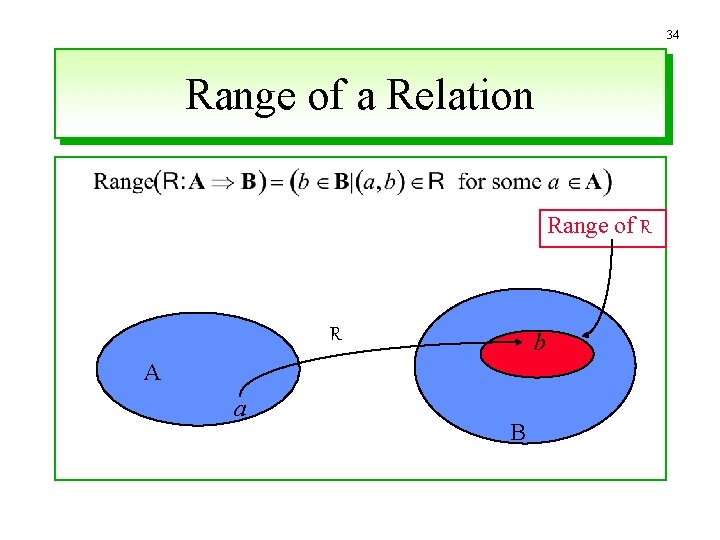
34 Range of a Relation Range of R R b A a B

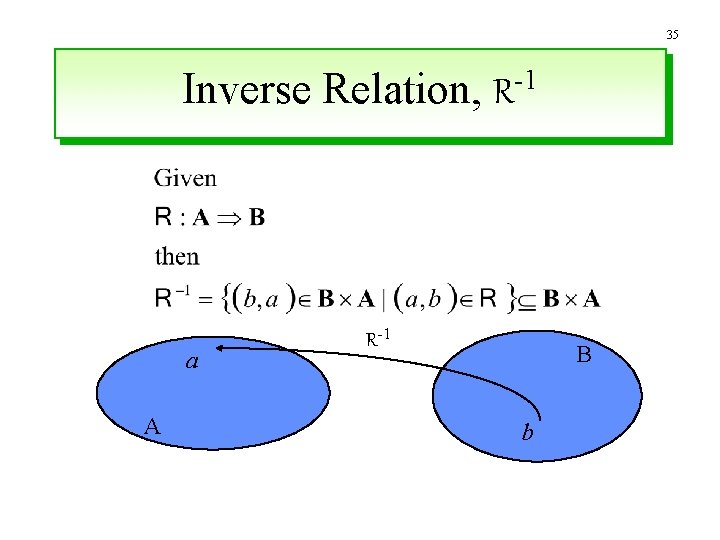
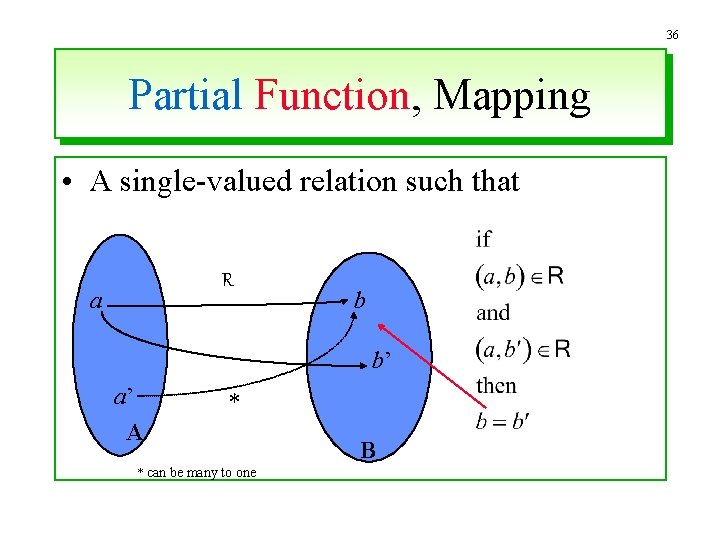
35 Inverse Relation, R-1 a A R-1 B b

36 Partial Function, Mapping • A single-valued relation such that R a b b’ a’ A * * can be many to one B

37 Partial Function – Also called the Image of a under R – Only one element of B for each element of A – Single-valued – Can be a many-to-one mapping

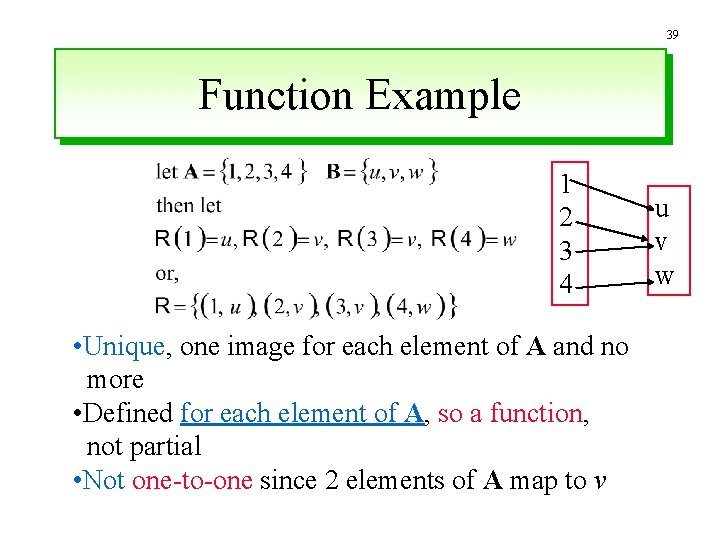
38 Function • A partial function with – A b corresponds to each a, but only one b for each a – Possibly many-to-one: multiple a’s could map to the same b

39 Function Example 1 2 3 4 • Unique, one image for each element of A and no more • Defined for each element of A, so a function, not partial • Not one-to-one since 2 elements of A map to v u v w

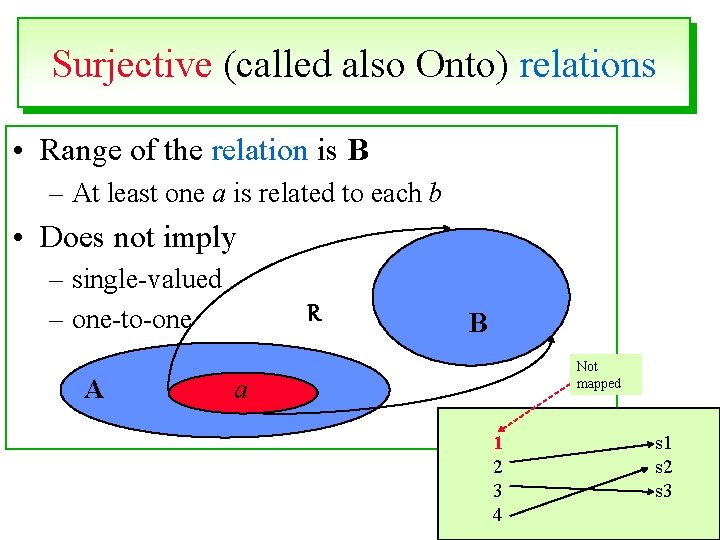
Surjective (called also Onto) relations 40 • Range of the relation is B – At least one a is related to each b • Does not imply – single-valued – one-to-one A R B Not mapped a 1 2 3 4 s 1 s 2 s 3

41 Injective, or One-to-One relations • “A relation between 2 sets such that pairs can be removed, one member from each set, until both sets have been simultaneously exhausted. ”

43 Bijective • A function which is both Injective and Surjective is Bijective. – Also called “one-to-one” and “onto” • A bijective function has an inverse, R-1, and it is unique

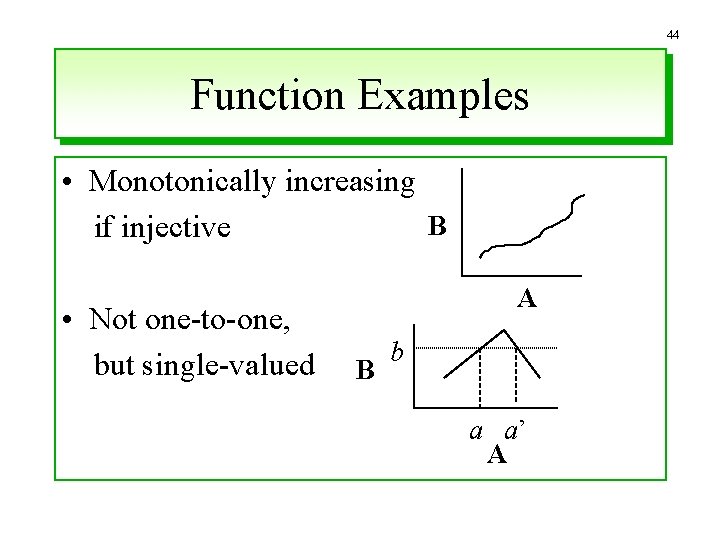
44 Function Examples • Monotonically increasing B if injective • Not one-to-one, but single-valued A B b a a’ A

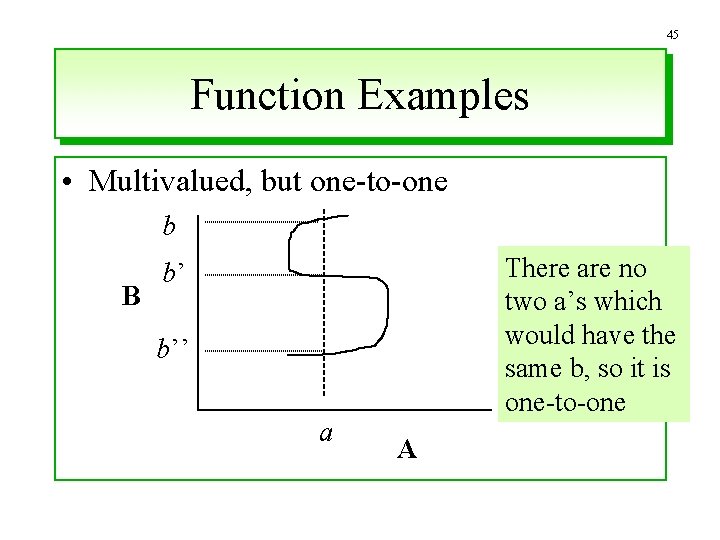
45 Function Examples • Multivalued, but one-to-one b B There are no two a’s which would have the same b, so it is one-to-one b’ b’’ a A