Morphisms of State Machines Sequential Machine Theory Prof

Morphisms of State Machines Sequential Machine Theory Prof. K. J. Hintz Department of Electrical and Computer Engineering Lecture 8 Updated and adapted by Marek Perkowski

Notation

Free Semi. Group

String or Word

Concatenation

Partition of a Set • Properties • pi are called “pi-blocks” of a partition, (A)

Types of Relations • • • Partial, Binary, Single-Valued System Groupoid Semi. Group Monoid Group

Partial Binary Single-Valued

Groupoid • Closed Binary Operation • Partial, Binary, Single-Valued System with • It is defined on all elements of S x S • Not necessarily surjective

Semi. Group • An Associative Groupoid – Binary operation, e. g. , multiplication – Closure – Associative • Can be defined for various operations, so sometimes written as

Closed Binary Operation • Division Is Not a Closed Binary Operation on the Set of Counting Numbers 6/3 = 2 = counting number 2/6 = ? = not a counting number • Division Is Closed Over the Set of Real Numbers.

Monoid Semigroup With an Identity Element, e.

Group Monoid With an Inverse

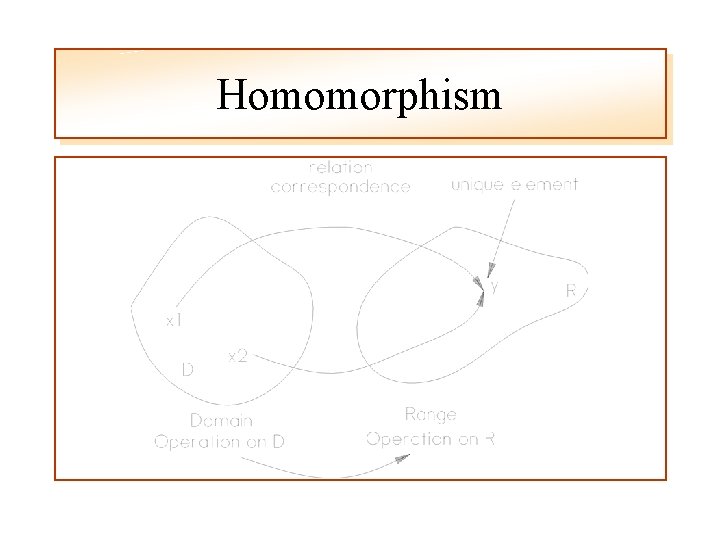
‘Morphisms’ Homomorphism (J&J) “A correspondence of a set D (the domain) with a set R (the range) such that each element of D determines a unique element of R [single-valued] and each element of R is the correspondent of at least one element of D. “ and. . .

Homomorphism “If operations such as multiplication, addition, or multiplication by scalars are defined for D and R, it is required that these correspond. . . ” and. . .

Homomorphism “If D and R are groups (or semigroups) with the operation denoted by * and x corresponds to x’ and y corresponds to y’ then x * y must correspond to x’ * y’ “ Product of Correspondence = Correspondence of product

Homomorphism

Homomorphism • Correspondence must be – Single-valued: therefore at least a partial function – Surjective: each y in the R has at least one x in the D – Non-Injective: not one-to-one else isomorphism

Endomorphism • A ‘morphism’ which maps back onto itself • The range, R, is the same set as the domain, D, e. g. , the real numbers. ‘morphism’ R=D

Semi. Group Homomorphism

Semi. Group Homomorphism

Sm. Gp. Hm. Mphsm. Example* *Larsen, Intro to Modern Algebraic Concepts, p. 53

Sm. Gp. Hm. Mphsm. Example* Is the relation • single-valued? – Each symbol of D maps to only one symbol of R • surjective? – Each symbol of R has a corresponding element in D • not-injective? – e and g 4 correspond to the same symbol, 0

Sm. Gp. Hm. Mphsm. Example* Do the results of operations correspond? same

Monoid Homomorphism

Isomorphism • An Isomorphism Is a Homomorphism Which Is Injective • Injective: One-to-One Correspondence – A relation between two sets such that pairs can be removed, one member from each set until both sets have been simultaneously exhausted

Semi. Group Isomorphism Injective Homomorphism

Isomorphism Example* • Define two groupoids – non-associative semigroups – groups without an inverse or identity element • SG 1: • SG 2: *Ginzberg, pg 10 A 1 = { positive real numbers } *1 = multiplication = * A 2 = { positive real numbers } *2 = addition = +

Isomorphism Example

Semi. Group Isomorphism

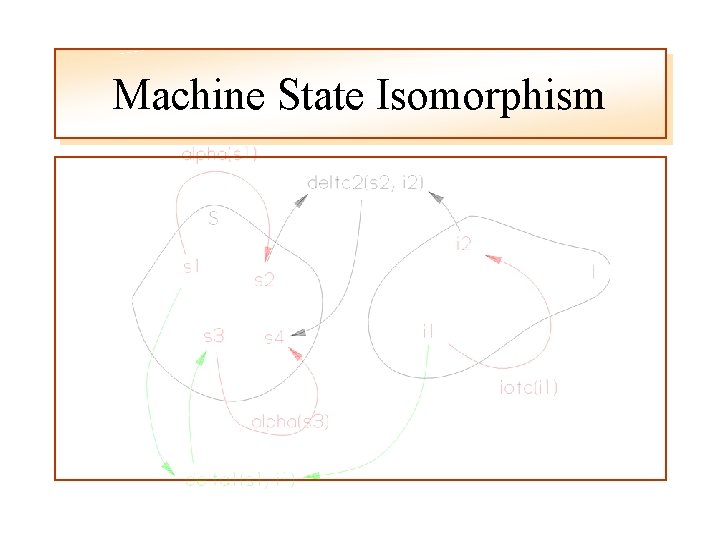
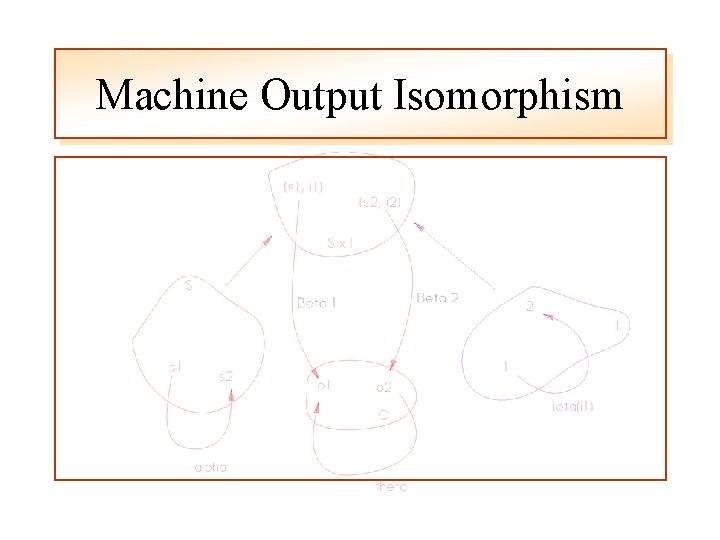
Machine Isomorphisms • Input-output isomorphism, but usually abbreviated to just isomorphism • An I/O isomorphism exists between two machines, M 1 and M 2 if there exists a triple

Machine Isomorphisms

Machine Isomorphisms Interpret

Machine State Isomorphism

Machine Output Isomorphism

Homo- vice Iso- Morphism Reduction Homomorphism • Shows behavioral equivalence between machines of different sizes • Allows us to only concern ourselves with minimized machines (not yet decomposed, but fewest states in single machine) • If we can find one, we can make a minimum state machine

Homo- vice Iso- Morphism Isomorphism • Shows equivalence of machines of identical, but not necessarily minimal, size • Shows equivalence between machines with different labels for the inputs, states, and/or outputs

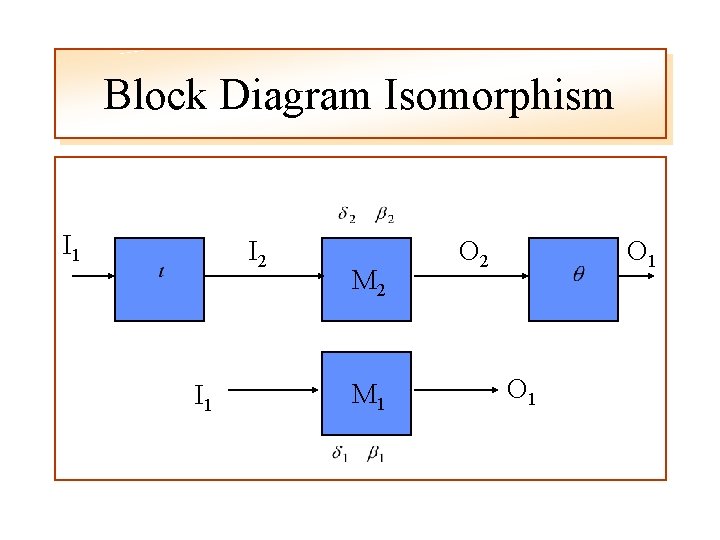
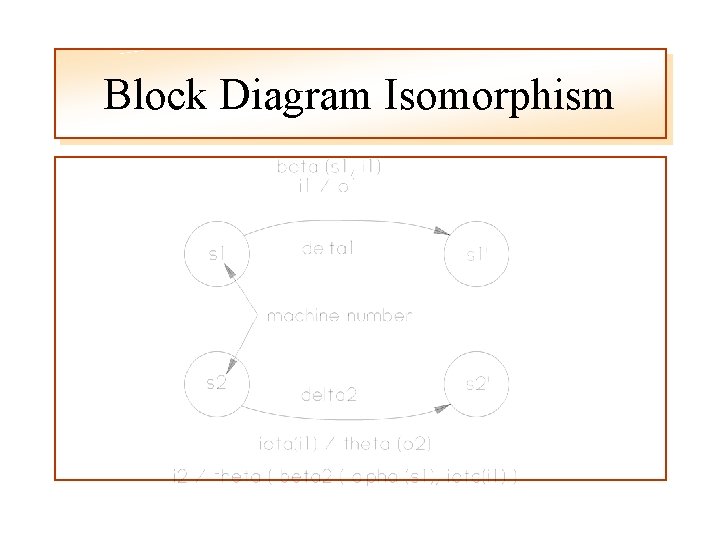
Block Diagram Isomorphism I 1 I 2 I 1 M 2 M 1 O 2 O 1

Block Diagram Isomorphism

Block Diagram Isomorphism which is the same as the preceding state diagram and block diagram definitions therefore M 1 and M 2 are Isomorphic to each other

Machine Information • Since the Inputs and Outputs Can Be Mapped Through Isomorphisms Which Are Independent of the State Transitions, All of the State Change Information Is Maintained in the Isomorphic Machine • Isomorphic Machines Produce Identical Outputs

Output Equivalence

Identity Machine Isomorphism

Inverse Machine Isomorphism

Machine Equivalence

Machine Homomorphism

Machine Homomorphism • If alpha is injective, then have isomorphism – “State Behavior” assignment, – “Realization” of M 1 • If alpha not injective – “Reduction Homomorphism”

Behavioral Equivalence

Behavioral Equivalence