Morphisms of State Machines Sequential Machine Theory Prof











































- Slides: 50

Morphisms of State Machines Sequential Machine Theory Prof. K. J. Hintz Department of Electrical and Computer Engineering Lecture 7 Updated and adapted by Marek Perkowski

Notation

Free Semi. Group

String or Word

Concatenation

Partition of a Set • Properties • pi are called “pi-blocks” of a partition, (A)

Types of Relations • • • 1. Partial, Binary, Single-Valued System 2. Groupoid 3. Semi. Group 4. Monoid 5. Group

Partial Binary Single-Valued

Groupoid • Closed Binary Operation • Partial, Binary, Single-Valued System with • It is defined on all elements of S x S • Not necessarily surjective arguments a a a b c c c Also: b c b a a b a c a(ba) = ac = a (ab) a = ba = c value Surjective: Surjective each y in the R has at least one x in the D

Semi. Group • An Associative Groupoid – Binary operation, e. g. , multiplication – Closure – Associative • Can be defined for various operations, so sometimes written as a a a b b c c a a b

Closed Binary Operation • Division Is Not a Closed Binary Operation on the Set of Counting Numbers 6/3 = 2 = counting number 2/6 = ? = not a counting number • Division Is Closed Over the Set of Real Numbers.

Monoid Semigroup With an Identity Element, e. a a a b b c c a a b

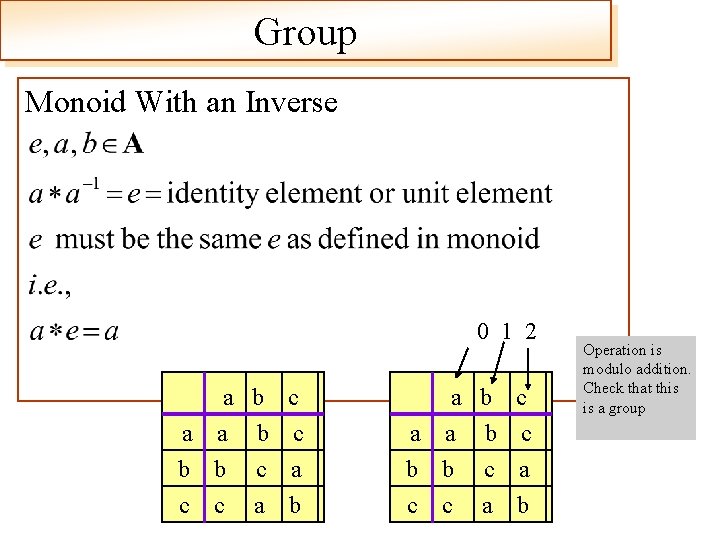
Group Monoid With an Inverse 0 1 2 a a a b b c c b c b c c a a b Operation is modulo addition. Check that this is a group

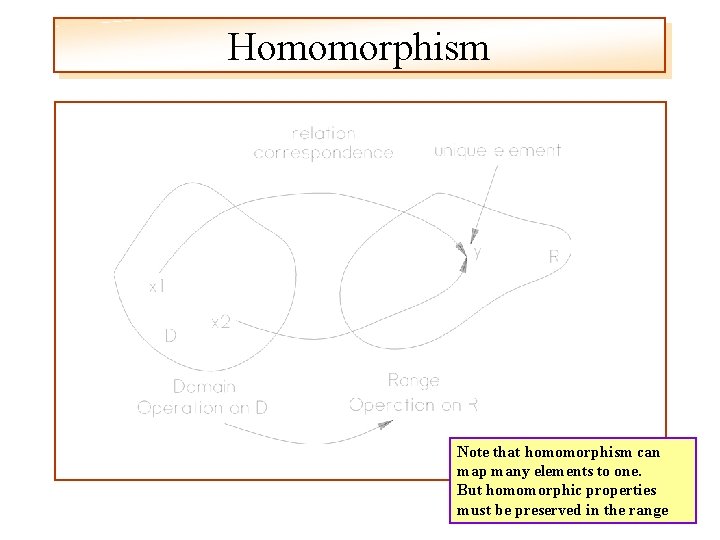
‘Morphisms’ Homomorphism “A correspondence of a set D (the domain) with a set R (the range) such that each element of D determines a unique element of R [single-valued] and each element of R is the correspondent of at least one element of D. “ and. . .

Homomorphism continued “If operations such as multiplication, addition, or multiplication by scalars are defined for D and R, it is required that these correspond. . . ” and. . .

Example: Homomorphism of groups “If D and R are groups (or semigroups) with the operation denoted by * and x corresponds to x’ and y corresponds to y’ then x * y must correspond to x’ * y’ “ Product of Correspondence = Correspondence of product

Homomorphism Note that homomorphism can map many elements to one. But homomorphic properties must be preserved in the range

Homomorphism preserves correspondence • Correspondence must be – Single-valued: Single-valued therefore at least a partial function – Surjective: Surjective each y in the R has at least one x in the D – Non-Injective: not one-to-one else isomorphism

Endomorphism • Question: What is endomorphism? • Answer: An endomorphism is a ‘morphism’ which maps back onto itself • The range, R, is the same set as the domain, D, e. g. , the real numbers. R=D ‘morphism’

Semi. Group Homomorphism Operation in range Operation in domain

Graphical Explanation of Homomorphism of Semi-Groups Operation in domain Operation in range

Homomorphism of Semi-Groups. Example* *Larsen, Intro to Modern Algebraic Concepts, p. 53 Ask a student to draw operations in domain and range and then show this homomorphism graphically

Homomorphism of Semi-Groups. Example* Is the relation • single-valued? – Each symbol of D maps to only one symbol of R • surjective? – Each symbol of R has a corresponding element in D • not-injective? – e and g 4 correspond to the same symbol, 0

Homomorphism of Semi-Groups. Example* Do the results of operations correspond? same

Homomorphism of Monoids

Isomorphism • An Isomorphism Is a Homomorphism Which Is Injective • Injective: One-to-One Correspondence – A relation between two sets such that pairs can be removed, one member from each set until both sets have been simultaneously exhausted

Graphical illustration of Isomorphism of Semi-Groups Injective Homomorphism

Example of function Log being Isomorphism of two semi-groups • Define two groupoids – non-associative semigroups – groups without an inverse or identity element • SG 1: A 1 = { positive real numbers } *1 = multiplication = * • SG 2: A 2 = { positive real numbers } *2 = addition = + *Ginzberg, pg 10

Example of function Log being Isomorphism of two semi-groups Isomorphism Example (continued)

Graphical illustration of this Semi. Group Isomorphism

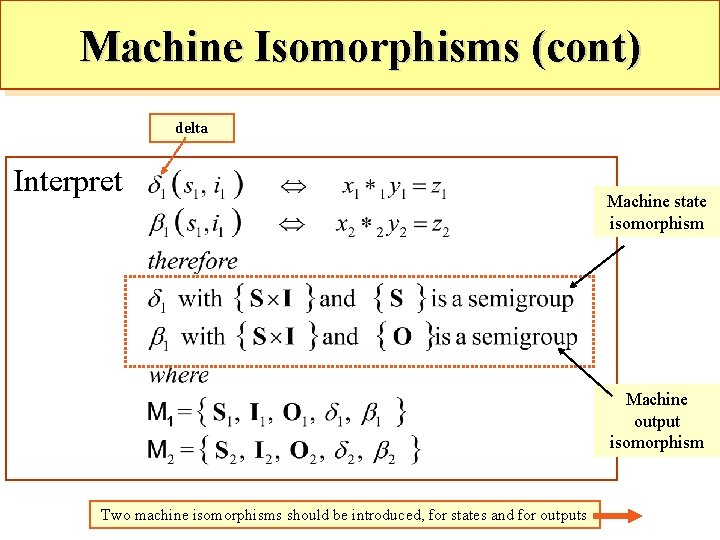
Machine Isomorphisms • Formally, it should be called Machine Inputoutput isomorphism, but usually abbreviated to just isomorphism • An I/O isomorphism exists between two machines, M 1 and M 2 if there exists a triple alpha

Machine Isomorphisms (cont) alpha iota

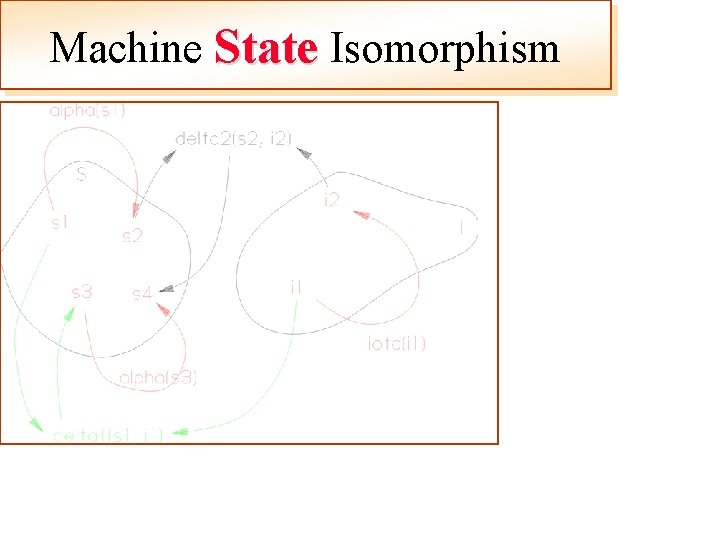
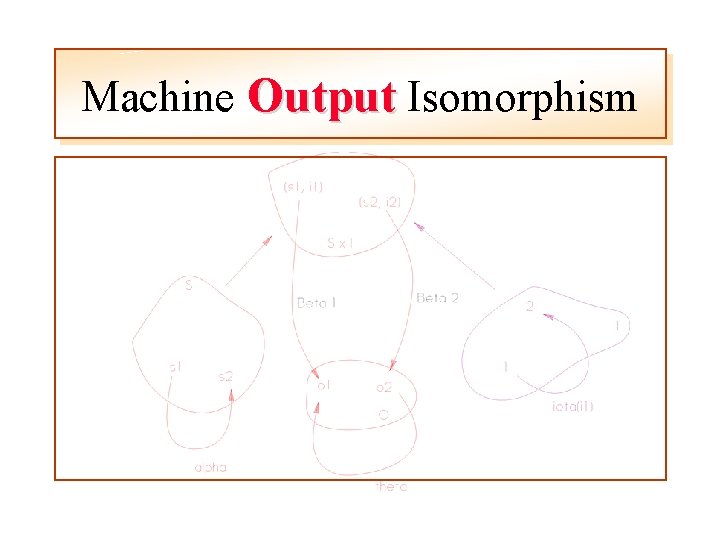
Machine Isomorphisms (cont) delta Interpret Machine state isomorphism Machine output isomorphism Two machine isomorphisms should be introduced, for states and for outputs

Machine State Isomorphism

Machine Output Isomorphism

Homo- vice Iso- Morphism Reduction Homomorphism • Shows behavioral equivalence between machines of different sizes • Allows us to only concern ourselves with minimized machines (not yet decomposed, but fewest states in single machine) • If we can find one, we can make a minimum state machine

Homo- vice Iso- Morphism Isomorphism • Shows equivalence of machines of identical, but not necessarily minimal, size • Shows equivalence between machines with different labels for the inputs, states, and/or outputs

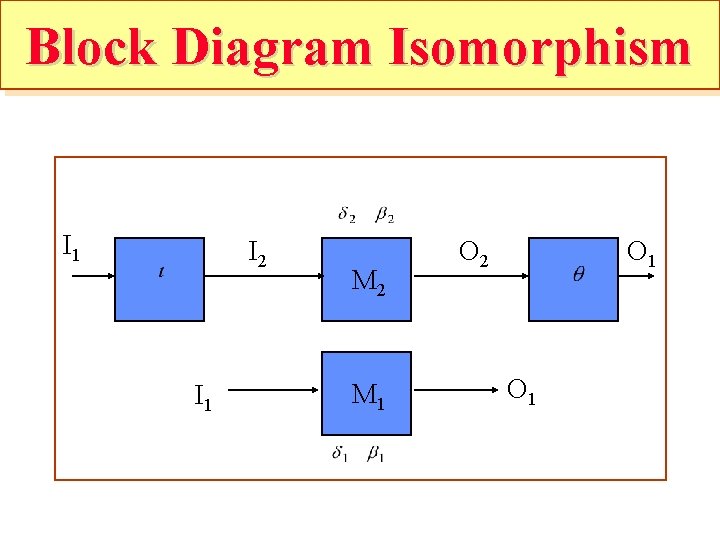
Block Diagram Isomorphism I 1 I 2 I 1 M 2 M 1 O 2 O 1

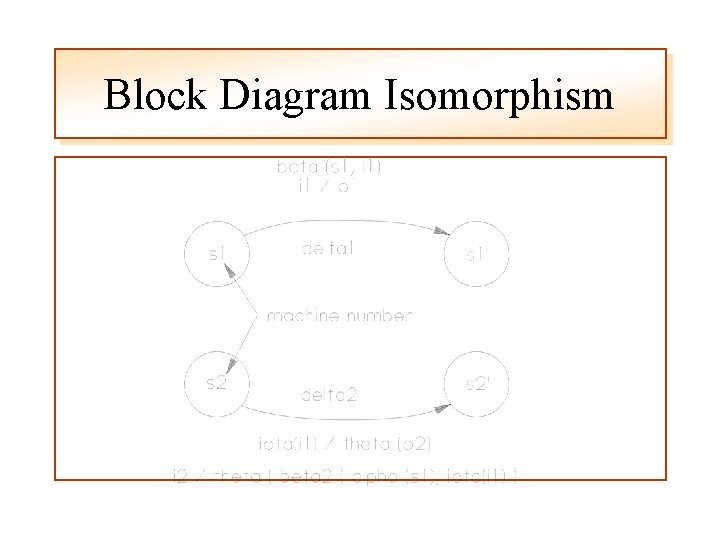
Block Diagram Isomorphism

Block Diagram Isomorphism which is the same as the preceding state diagram and block diagram definitions therefore M 1 and M 2 are Isomorphic to each other

Information in Isomorphic Machines • Since the Inputs and Outputs Can Be Mapped Through Isomorphisms Which Are Independent of the State Transitions, All of the State Change Information Is Maintained in the Isomorphic Machine • Isomorphic Machines Produce Identical Outputs

Output Equivalence Output strings of one machine are equivalent to output strings of other machine

Identity Machine Isomorphism Al three are identity functions

Inverse Machine Isomorphism

Machine Equivalence Remember: machine isomorphism is an equivalence relation defined on M

Machine Homomorphism

Machine Homomorphism • If alpha is injective, then have isomorphism – “State Behavior” assignment, – “Realization” of M 1 • If alpha not injective – “Reduction Homomorphism”

Behavioral Equivalence of two State Machines

Behavioral Equivalence

Homework Problem • Take an arbitrary machine M and minimize it to machine M 2 which has less states. • Next specify the homomorphism between Machine M and Machine M 2 that corresponds to the relation of combining compatible states. • To specify this homomorphism use the formalisms and notations from this lecture.
 Finite state machine sequential circuits
Finite state machine sequential circuits Durum makinesi nedir
Durum makinesi nedir Sequential machine
Sequential machine Finite state machine vending machine example
Finite state machine vending machine example Finite state machine verilog
Finite state machine verilog Binary state assignment
Binary state assignment Sequential machine
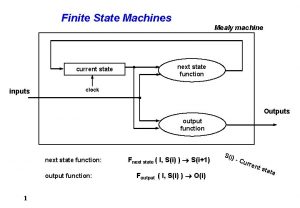
Sequential machine Mealy machine
Mealy machine Sequential machine
Sequential machine Sequential machine
Sequential machine Gears and pulley
Gears and pulley In an incompletely specified machine
In an incompletely specified machine State machines digital electronics
State machines digital electronics Theory of machines
Theory of machines Mealy and moore model
Mealy and moore model Mealy to moore conversion
Mealy to moore conversion Differentiate between simple machine and compound machine
Differentiate between simple machine and compound machine Vending machine state diagram
Vending machine state diagram State machine diagram example
State machine diagram example Tcp connection management finite state machine
Tcp connection management finite state machine Quartus technology
Quartus technology State diagram to ladder logic
State diagram to ladder logic Distributed state machine
Distributed state machine State diagram for washing machine
State diagram for washing machine Quartus 2 web edition
Quartus 2 web edition One hot state assignment
One hot state assignment Limitations of finite automata
Limitations of finite automata Mealy state machine
Mealy state machine Finite state machine with datapath
Finite state machine with datapath Mealy
Mealy Finite state machine minimization
Finite state machine minimization Algorithmic state machine chart
Algorithmic state machine chart Vhdl finite state machine
Vhdl finite state machine Traffic light finite state machine
Traffic light finite state machine Tcp connection management finite state machine
Tcp connection management finite state machine State machine replication blockchain
State machine replication blockchain Submachine state in state diagram
Submachine state in state diagram Machine design
Machine design Finite state machine vhdl
Finite state machine vhdl Finite state machine elevator
Finite state machine elevator State machine design
State machine design Activity state diagram
Activity state diagram Gray code counter vhdl
Gray code counter vhdl One-hot state machine
One-hot state machine Finite state machine
Finite state machine Ospf finite state machine
Ospf finite state machine Finite state machine
Finite state machine Finite state machine game
Finite state machine game State machine diagram example
State machine diagram example Jtag state machine
Jtag state machine Uml building blocks in software engineering
Uml building blocks in software engineering