Equivalence DFA NDFA Sequential Machine Theory Prof K

Equivalence, DFA, NDFA Sequential Machine Theory Prof. K. J. Hintz Department of Electrical and Computer Engineering Lecture 2 Updated and modified by Marek Perkowski

Equivalence Relation on A • An Equivalence Relation (Not Relationship) Is Not an Equality Relation • A Relation is an Equivalence Relation if and only if (iff) it is: – Reflexive – Symmetric – Transitive

Equivalence Relation on A

Non-Algebraic Equivalence Relation Example Equivalence Relation on the Set of All Triangles on a Plane “is congruent to” or “is similar to” – Reflexive, each triangle is similar to itself,

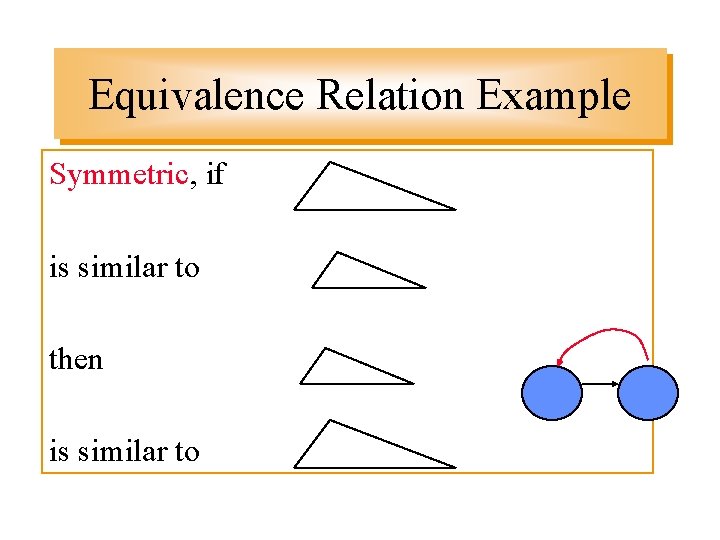
Equivalence Relation Example Symmetric, if is similar to then is similar to

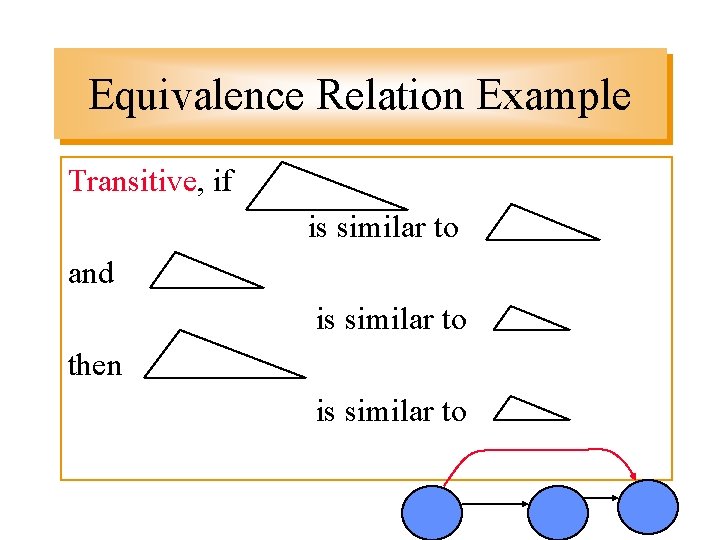
Equivalence Relation Example Transitive, if is similar to and is similar to then is similar to

Inclusion Relation

Inclusion Relation Example Illustrate a bigger lattice graphically

Partition Notation • Overbar Indicates States Which Are Elements of the Same -block. • Single States Are Not Normally Listed

Relations May Be Orderings • Partial Ordering • Total Ordering, aka Chain • Well Ordering (not discussed here)

Partial Ordering (PO) • Given an Inclusion Relation, R: s s’, Defined on some Elements of the Set S such that s, s’ S, R Is a Partial Ordering If It Is: – Reflexive – Anti-Symmetric (asymmetric) – Transitive – Not all orderings are specified, therefore partial Illustrate on a lattice

Properties of Partial Orderings – Reflexive • s s for all s S – Anti-Symmetric (asymmetric) e. g. , let than” : “older if Sam is older than Bill, then Bill cannot be older than Sam But if this symbol means older or the same age, then OK

Properties of PO – Transitive e. g. , If the Redskins beat the Patriots and the Patriots beat the Cowboys then the Redskins will beat the Cowboys

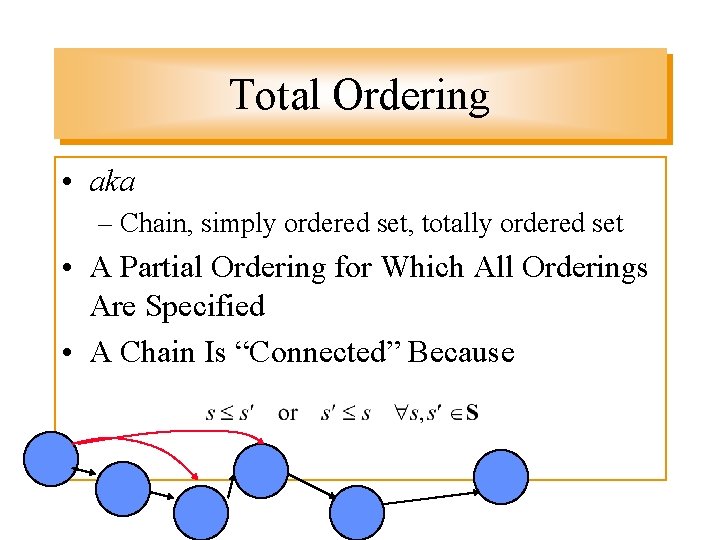
Total Ordering • aka – Chain, simply ordered set, totally ordered set • A Partial Ordering for Which All Orderings Are Specified • A Chain Is “Connected” Because

POSET • Partially Ordered SET – A set on which a partial ordering is specified – ( S, ) where is defined – Not a chain since not all elements are connected • We Will Revisit This Concept in a later part of the Course

Finite Automata A Deterministic semi-automaton*, aka Completely Specified Deterministic Semiautomaton is a Triple with no Mealy machine output function, Beta ( ) * Ginzburg, 1968

FSM Set Properties S sa sc I ib

Language Recognizer • aka, Rabin-Scott Automata (machine), Automaton, Language Recognizer • A Recognizer Is a Quintuple of Sets with S, I, as before

Kleene Star • a* = e, a, aaa, aaaa, . . . • The Kleene Star, *, means NONE or more occurrences of something • Star is an overloaded operator so be aware of context • a+= ONE or more occurrences of something. • a+ is Kleene Star less the null string, .

Kleene Closure • Kleene Closure Is Not Identical to Kleene Star – “*” Symbol is the same (overloaded) • Kleene Closure/Star Closure – Found in descriptions of formal language – Language consisting of all strings over some alphabet

String • An Ordered Concatenation of Symbols From an Alphabet • Used in Place of “Word” to Decouple From Common Concept of Word in Informal Language • If = { a, 1, 0, b, % } then a “ 1%0 b” is a string.

Recognizer If x I*, i. e. , a string of input symbols selected from the set of allowable input symbols, and the application of x to the recognizer results in a final state F, then the recognizer “accepts” the string.

Strings A String, x, Is Accepted by a Recognizer Left-most Letter First, i. e. , if the input to a recognizer is a string w, and if w= w’ then is the first letter of the string which causes a state transition. Subsequent letters from left to right do the same.

State Transition Let There Be Two Configurations for a Machine 1 q S q’

String Example Let w=abba then w = a w’ and w’ = b b a

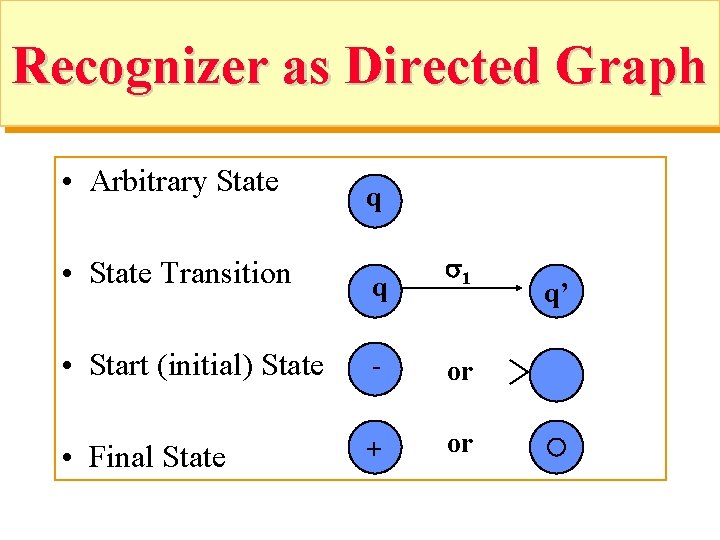
Recognizer as Directed Graph • Arbitrary State q • State Transition q 1 • Start (initial) State - or • Final State + or q’

Recognizer Examples Let I = { a, b } • Accepts no strings since no final state a, b • Accepts all strings a, b • Dead State a, b -

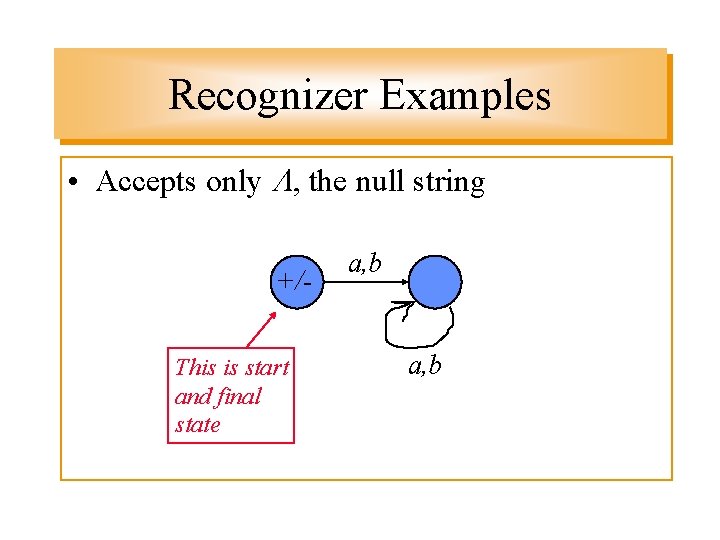
Recognizer Examples • Accepts only , the null string +/This is start and final state a, b

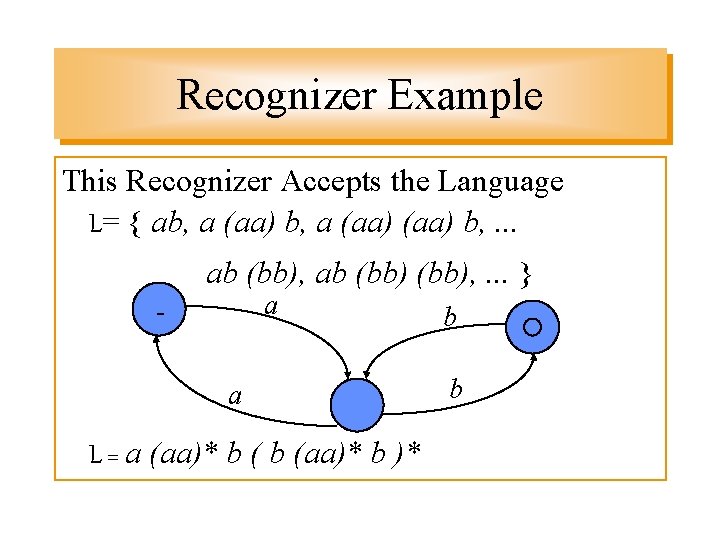
Recognizer Example This Recognizer Accepts the Language L= { ab, a (aa) b, . . . ab (bb), . . . } a a L = a (aa)* b b

New Example: Rabin-Scott Machine Now we transform this table to a graph

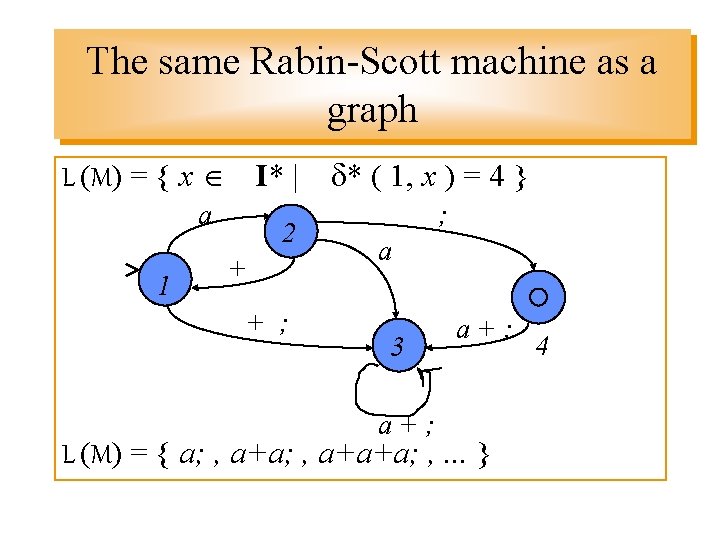
The same Rabin-Scott machine as a graph L (M) = { x I* | a 1 2 + + ; * ( 1, x ) = 4 } ; a 3 a+; L (M) = { a; , a+a+a; , . . . } 4

Non-Deterministic FSM A Non-deterministic Finite Automata Is a Quintuple with S, I, s 0, F as in a recognizer, but,

Non-Deterministic FSM • State May Change – to two (or any) different states in response to the same input at the same state – in response to a string rather than just a single element from the set of inputs – in response to a null string input

DFA-NDFA Theorem • Every NDFA Can Be Replaced by an Equivalent DFA • Equivalent Means Not Only Accepting All Strings Accepted by the NDFA, but Also NOT Accepting Any Other strings

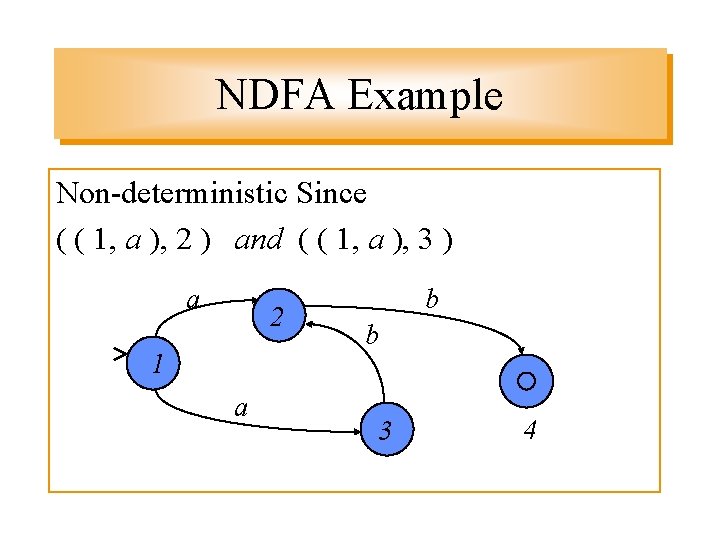
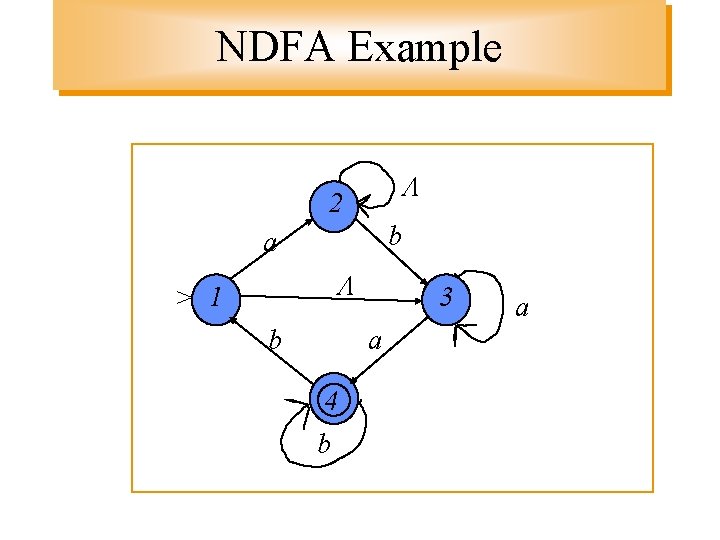
NDFA Example Non-deterministic Since ( ( 1, a ), 2 ) and ( ( 1, a ), 3 ) a 2 11 a b b 3 4

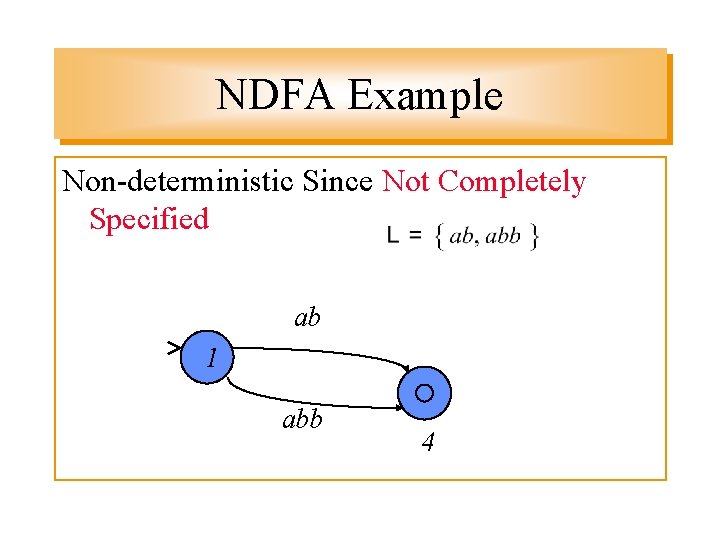
NDFA Example Non-deterministic Since Not Completely Specified ab 1 abb 4

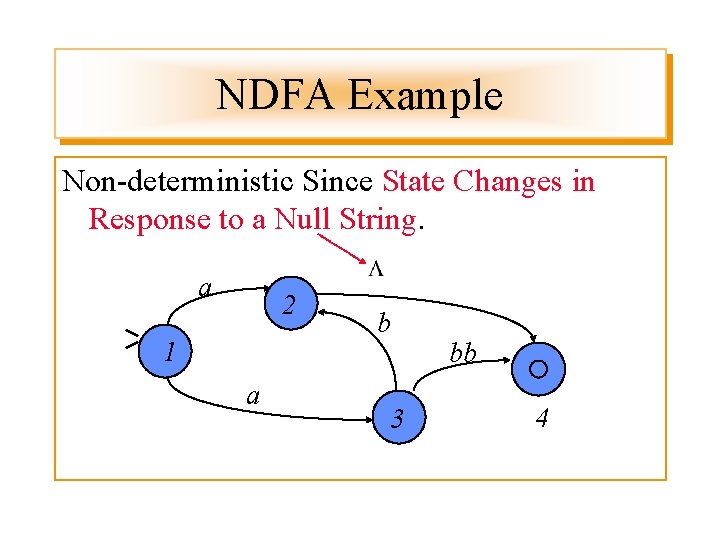
NDFA Example Non-deterministic Since State Changes in Response to a Null String. a 2 1 a b 3 bb 4

NDFA to DFA • Theorem – For each NDFA there is an equivalent DFA • Constructive Proof • 4 Difficulties to Resolve – Missing transitions – Single transitions due to | strings | > 1 – Transitions due to strings – Multiple transitions

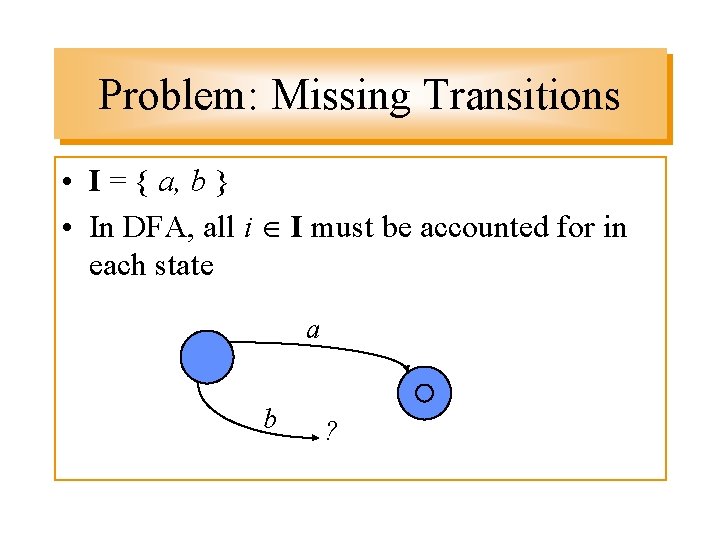
Problem: Missing Transitions • I = { a, b } • In DFA, all i I must be accounted for in each state a b ?

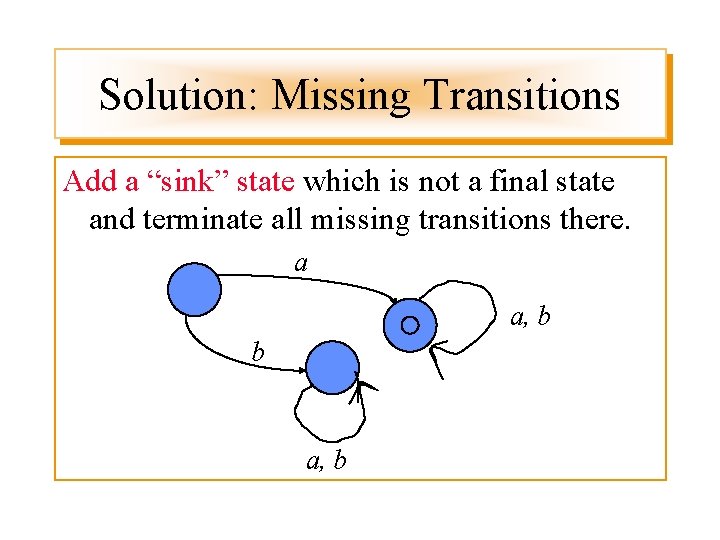
Solution: Missing Transitions Add a “sink” state which is not a final state and terminate all missing transitions there. a a, b b a, b

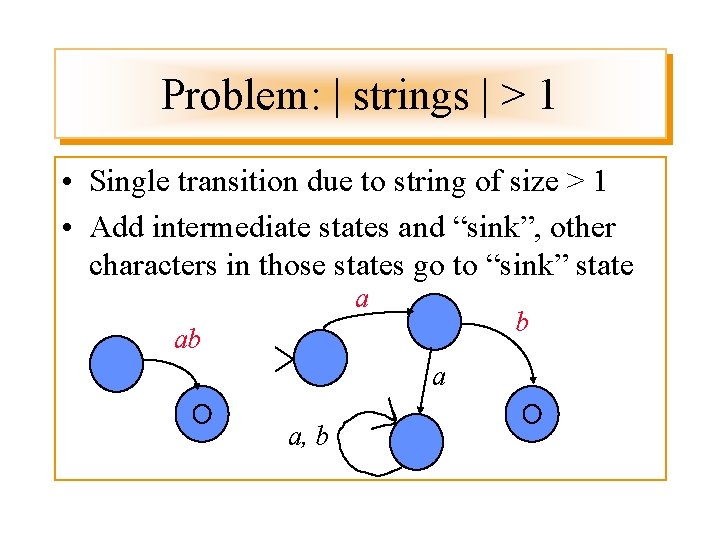
Problem: | strings | > 1 • Single transition due to string of size > 1 • Add intermediate states and “sink”, other characters in those states go to “sink” state a b ab a a, b

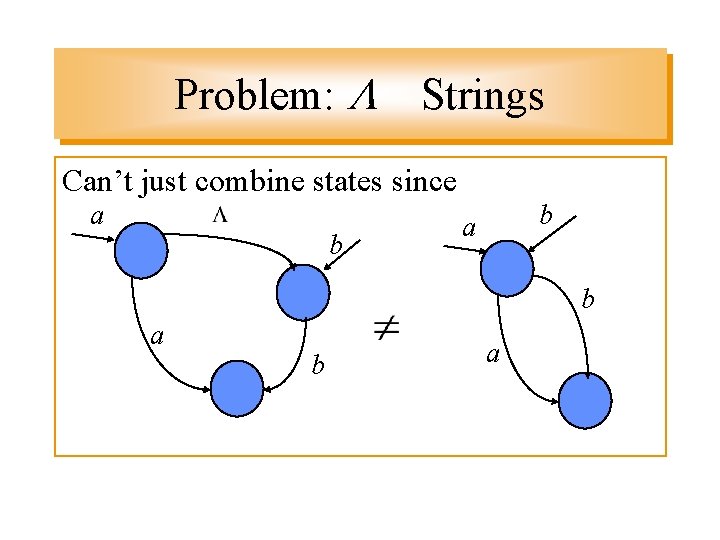
Problem: Strings Can’t just combine states since a b b a b a

Solution: Strings & Multiple Transitions • Eliminate by defining the set of next states which occur in response to no input, call this function E( ) • E( ) is called the “equivalents of ( )

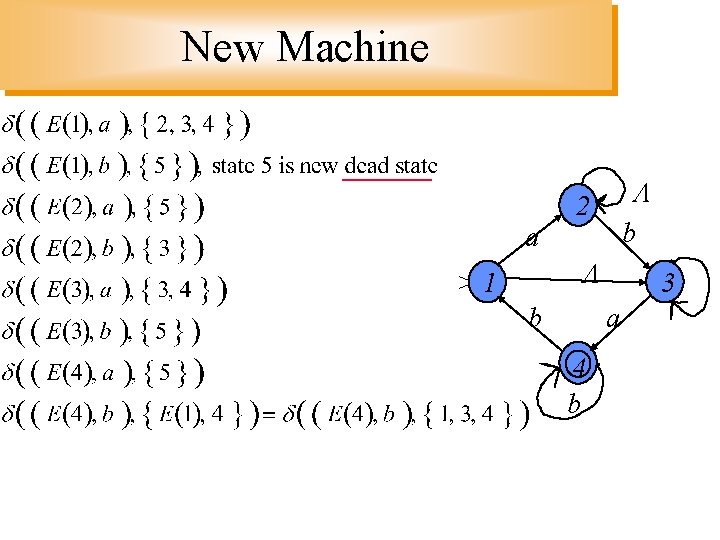
NDFA Example 2 b a > 1 b 3 a 4 b a

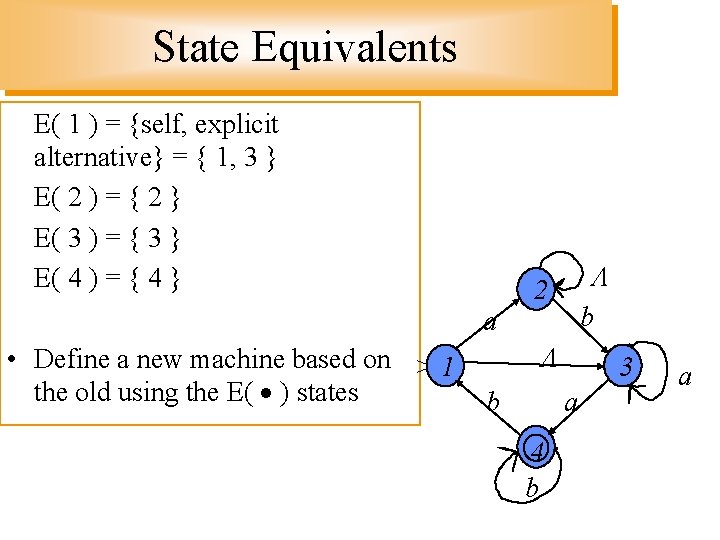
State Equivalents E( 1 ) = {self, explicit alternative} = { 1, 3 } E( 2 ) = { 2 } E( 3 ) = { 3 } E( 4 ) = { 4 } 2 b a • Define a new machine based on > 1 the old using the E( ) states b 3 a 4 b a

New Machine 2 b a >1 b 3 a 4 b a

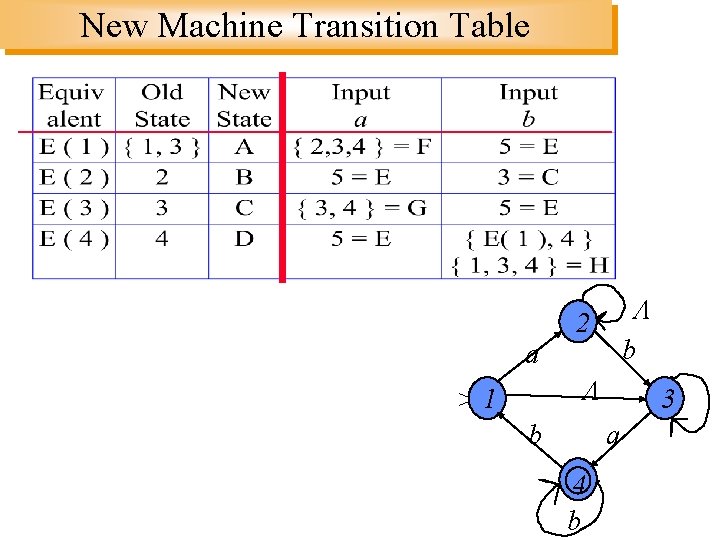
New Machine Transition Table 2 b a >1 b 3 a 4 b a

New Machine Transition Table a >1 2 b b 3 a 4 b a

New Machine Transition Table 2 b a >1 b 3 a 4 b

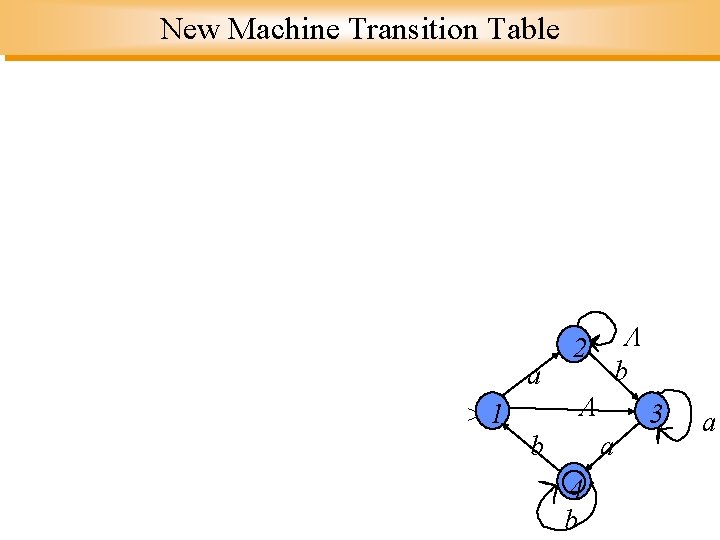
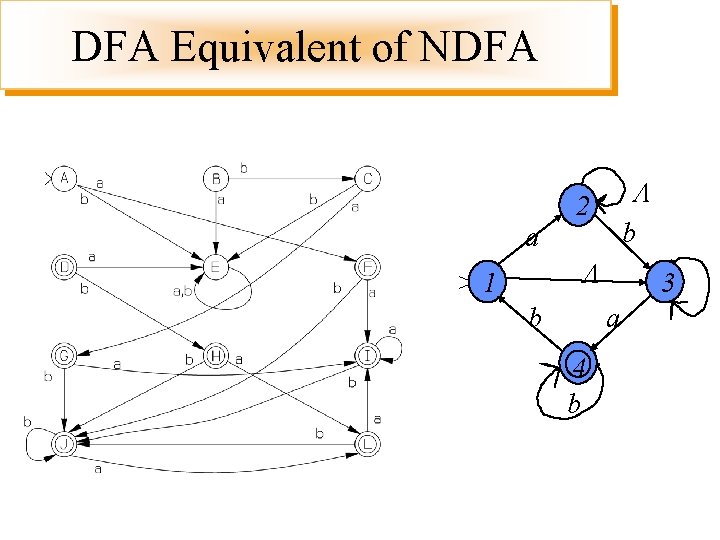
DFA Equivalent of NDFA 2 b a >1 b 3 a 4 b a

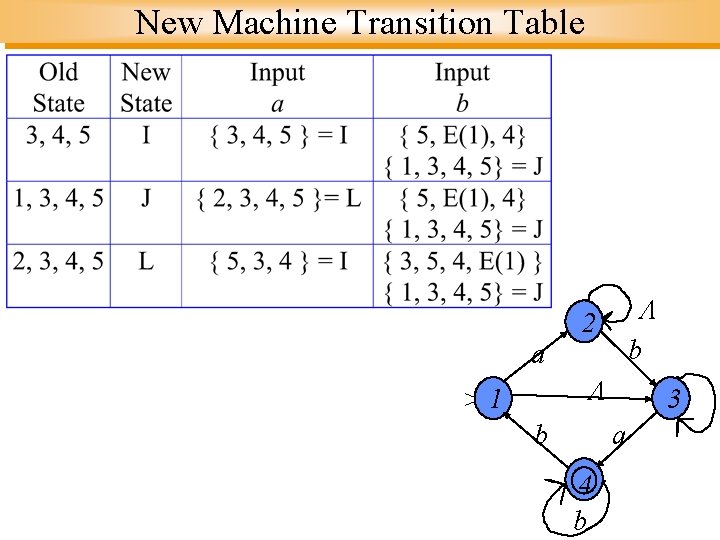
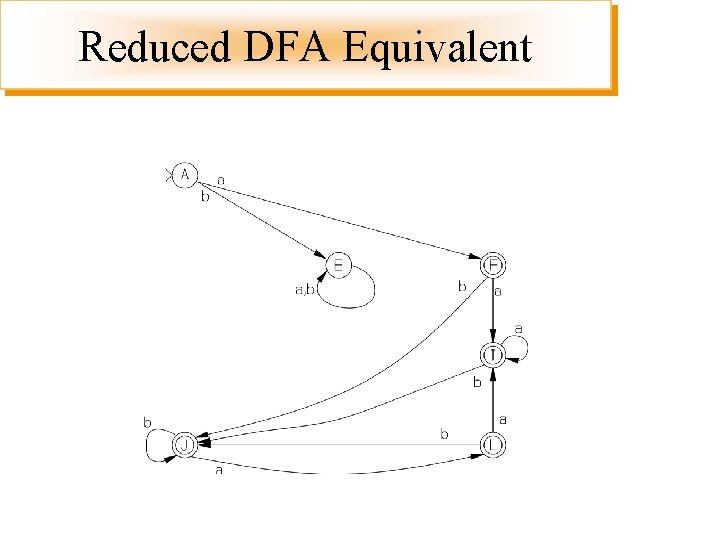
Reduced DFA Equivalent

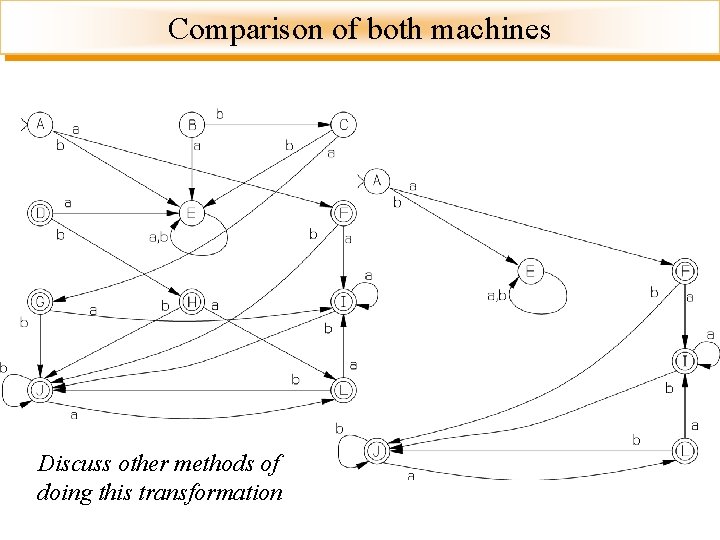
Comparison of both machines Discuss other methods of doing this transformation

Homework • This is only homework example. Another homework may be assigned. • 1. Describe any problem from real life, possibly related to your previous research, experience from other classes or otherwise as a non-deterministic finite automaton NDA. You may use Kleene star and empty symbols, if necessary. • 2. Convert it to a deterministic automaton DA. • 3. Try to minimize DA to Minimized MDA. • 4. Realize MDA using JK Flip-Flops and logic gates. • 5. Analyze its behavior using the logical diagram. Compare to the initial description. Draw and write conclusions.