Regular Expression Manipulation FSM Model Sequential Machine Theory

Regular Expression Manipulation FSM Model Sequential Machine Theory Prof. K. J. Hintz Department of Electrical and Computer Engineering Lecture 5 Modifications by Marek Perkowski

Null Machine 3 Methods for Proving That a Machine Accepts No Words – By inspection • Any path from the start state to a final state means that at least one word is accepted by the machine – By state diagram manipulation • If a final state is relabeled as a start state, then the machine must accept at least one word

Null Machine – By converting the regular expression into a deterministic FA • If possible, FA must accept at least one word • Conversion to FA may not be possible – Machine may have no final states. – There is no path from the initial state to any final state. Give examples

Reachability Analysis Reachability analysis will show that this machine will never reach the final state starting from initial state. Show it. Discuss reachability for computer hardware and robotics

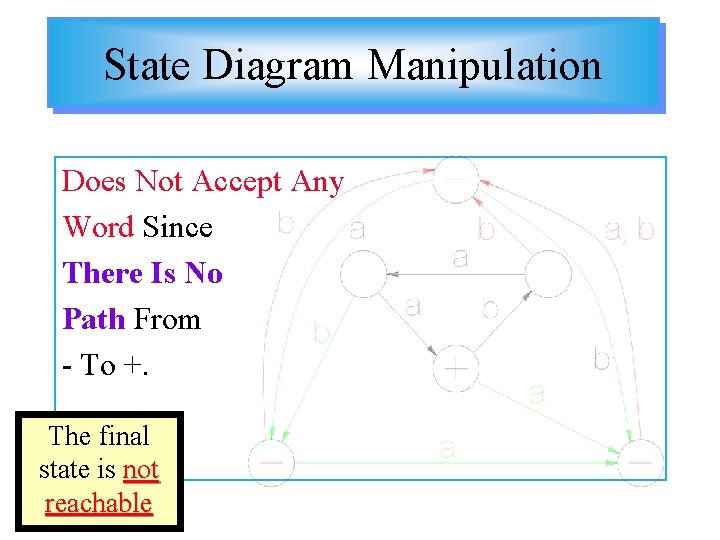
State Diagram Manipulation A procedure to determine if a machine accepts no strings 1. 2. 3. 4. 5. Remove all edges (arrows) to the start state. From the start state, identify all single-step “next states. ” Relabel these “next states” as start states and eliminate the edges used to get there. go to (b) If a final state is relabeled as a start state, then the machine must accept at least one word.

State Diagram Manipulation Does Not Accept Any Word Since There Is No Path From - To +. The final state is not reachable

The Complement Machine • A Complement Machine Accepts All Expressions Other Than Those Accepted by the Original Machine • Method – Change all non-final states into final states – Change all final states into non-final states – Leave start state unchanged

Language Decidability Methods for Determining If Two Regular Expressions Define the Same Language – Language Enumeration with 1: 1 correspondence between the 2 languages. – The regular languages can be accepted by identical FAs. – Generate This example demonstrates why it is useful to be able to check if language is empty This is like xor of languages

Language Overlap • If the Overlap Language Is NOT the Null Set, Then There Is Some Word in L 1 Which Is Not Accepted by L 2 and Vice Versa. • If the Overlap Language Accepts the Null String, Then the Languages Are Not Equal.

De. Morgan’s Theorem Applies Equally Well to Sets As Well As Boolean Algebra

Regular Expression Equivalence Methodology – Construct the complement machines – Apply De. Morgan’s theorem since it is difficult to form the intersect machine Show some special cases when it is easy to create the intersect machine

Regular Expression Equivalence Take the Unions of the Complemented and Non-complemented Several Times to Determine whether Language overlap is the Null Set or not

RE Equivalence Example* Two REs are represented by their equivalent FAs (FA 1 does = FA 2) *Cohen, Prob. 2, page 233. Obviously looking at these two machines we see that they are equivalent, but how to prove it? Try to use first machine minimization method and isomorphism state

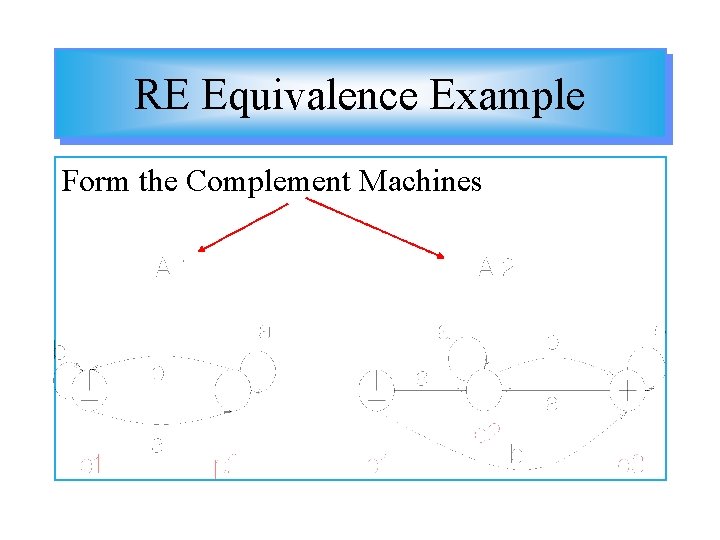
RE Equivalence Example Form the Complement Machines

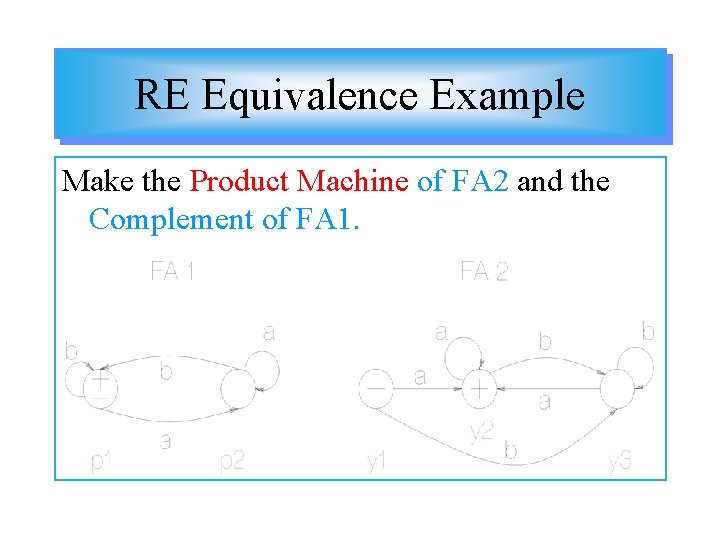
RE Equivalence Example Make the Product Machine of FA 2 and the Complement of FA 1.

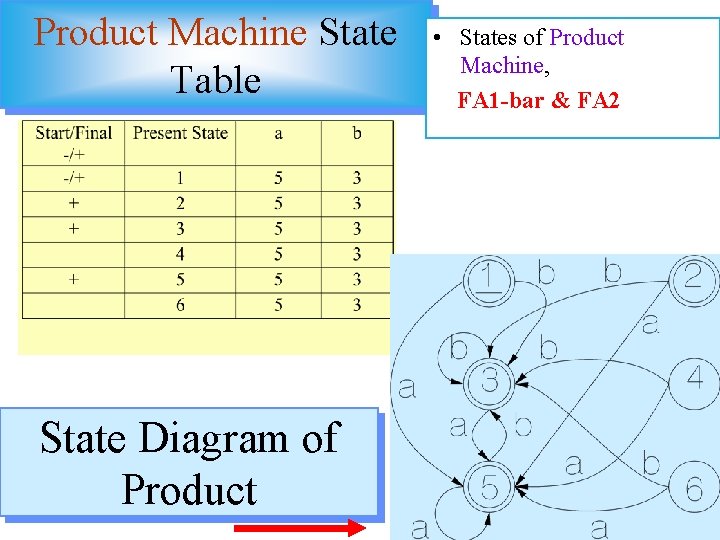
RE Equivalence Example • States of Product Machine, FA 1 -bar & FA 2 • Only One Start State / Multiple Final States

Product Machine State Table State Diagram of Product • States of Product Machine, FA 1 -bar & FA 2

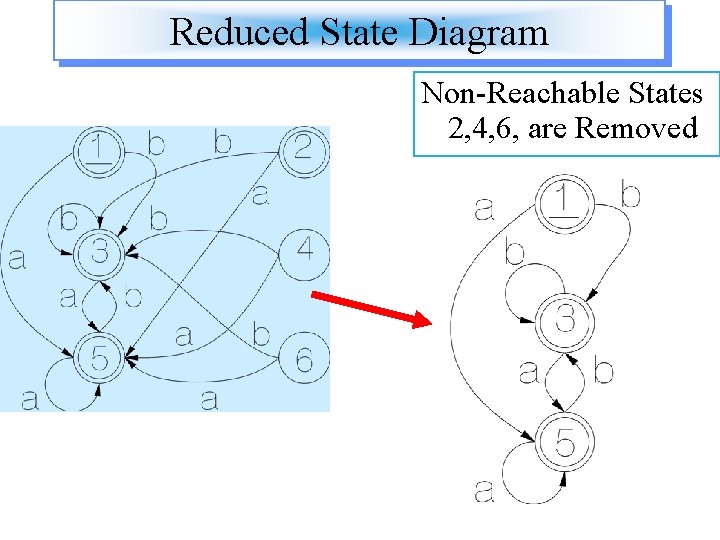
Reduced State Diagram Non-Reachable States 2, 4, 6, are Removed

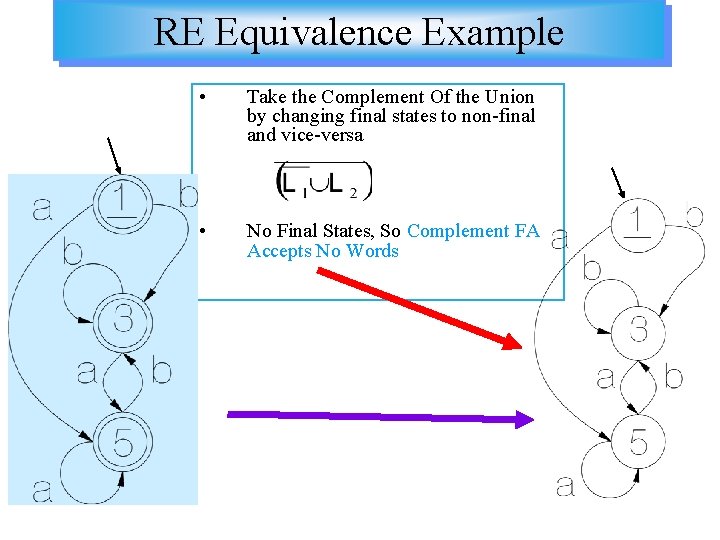
RE Equivalence Example • Take the Complement Of the Union by changing final states to non-final and vice-versa • No Final States, So Complement FA Accepts No Words

RE Equivalence Example Do the Same for the Right Term of Loverlap

RE Equivalence Example • Application of Same Procedure to Preceding Machine Also Results in No Recognizable Words. • Since Both Terms of Loverlap are Null, Then REs Are Equivalent Since Their Union Is Null. Finally we proved that these two machines are equivalent without the need to minimize them.

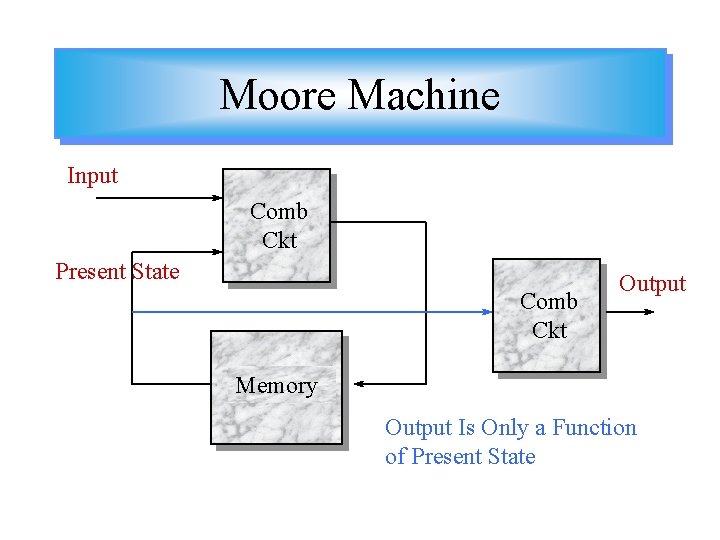
Moore & Mealy Machines • The Behavior of Sequential Machines Depends on Previous Inputs. – Moore Machine • Output only depends on present state – Mealy Machine • Output depends on both the present state and the present input

Moore & Mealy Machines Equivalent Descriptive Methods – Transition (state) table – Transition (state) diagram – Operational descriptions using set theory – (Language recognized by the machine)

Moore Machine Input Comb Ckt Present State Comb Ckt Output Memory Output Is Only a Function of Present State

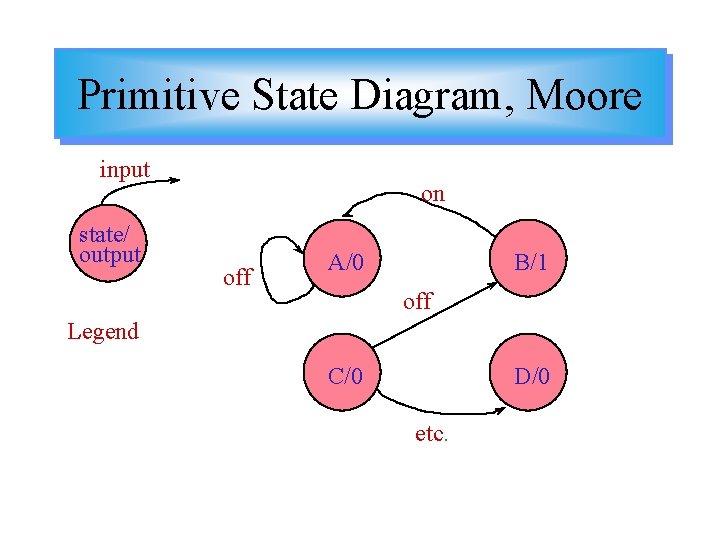
Primitive State Diagram, Moore input state/ output on off A/0 B/1 off Legend C/0 D/0 etc.

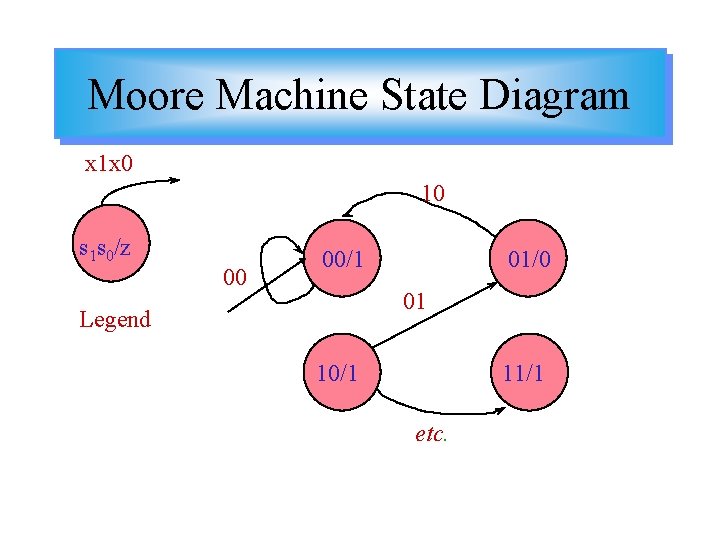
Moore Machine State Diagram x 1 x 0 10 s 1 s 0/z 00 00/1 01/0 01 Legend 10/1 11/1 etc.

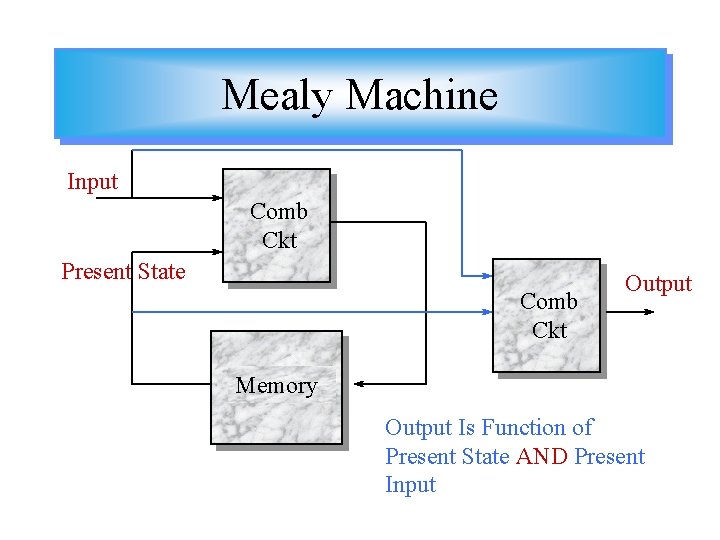
Mealy Machine Input Comb Ckt Present State Comb Ckt Output Memory Output Is Function of Present State AND Present Input

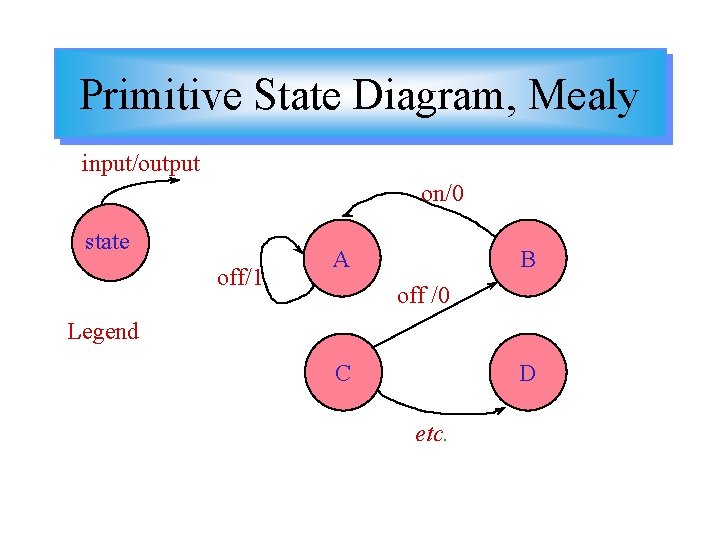
Primitive State Diagram, Mealy input/output on/0 state off/1 A B off /0 Legend C D etc.

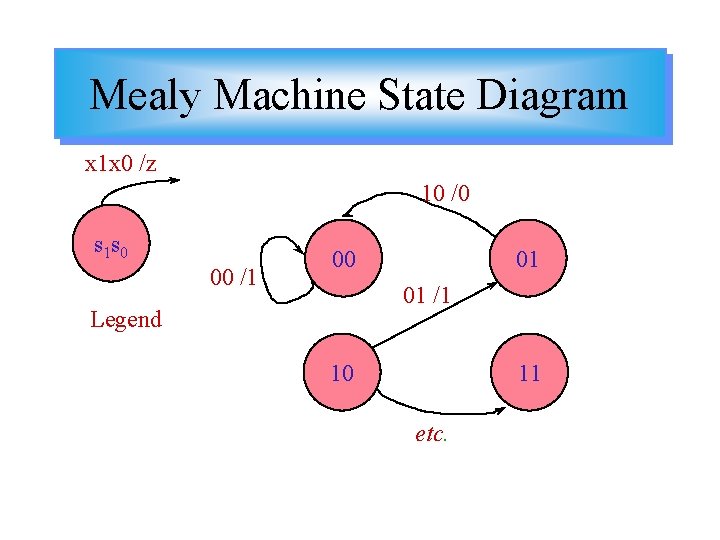
Mealy Machine State Diagram x 1 x 0 /z 10 /0 s 1 s 0 00 /1 00 01 01 /1 Legend 10 11 etc.

Transition Table

FSM Design Approaches • “One-Hot” – One flip-flop is used to represent each state – Costly in terms of discrete hardware, but trivial to design – Efficient in FPGAs because FF part of each CLB • Binary Coded State – n flip-flops used to store 2 n states – Most efficient – Need to account for unused states Review the one-hot coded machines and transition from non-deterministic to deterministic. Discuss parallel state machines and similar diagrams like Petri nets

FSM and Clocks • Synchronous FSMs may change state only when a unique input, the clock, occurs • Asynchronous FSMs may change state when input changes • Next state depends on present input and present state for both Moore and Mealy

Synchronous versus Asynchronous Machines in Design • Synchronous FSMs – Easier to design, turn the crank – Slower operation • Asynchronous – Harder to design because of potential for races, iterative solutions – Faster operation

Mealy “ 0101” Detector S: I: O: d: b: M = ( S, I, O, d, b ) { A, B, C, D } { ‘ 0’, ‘ 1’ } { 0, 1 } = { not detected, detected} next slide

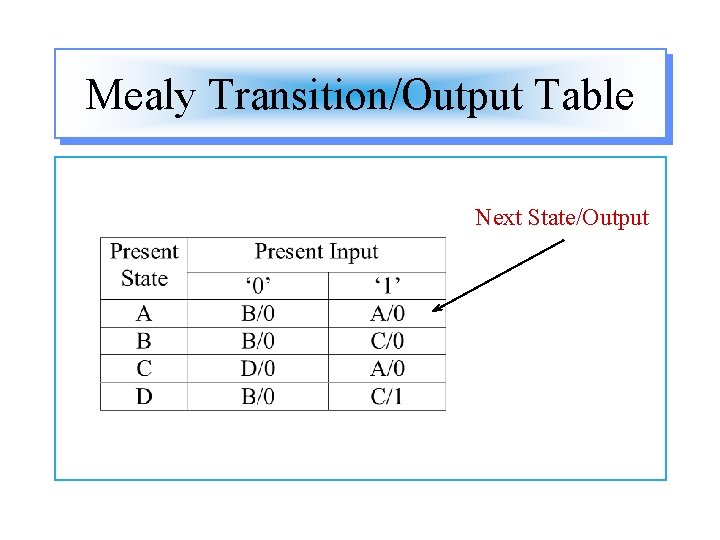
Mealy Transition/Output Table Next State/Output

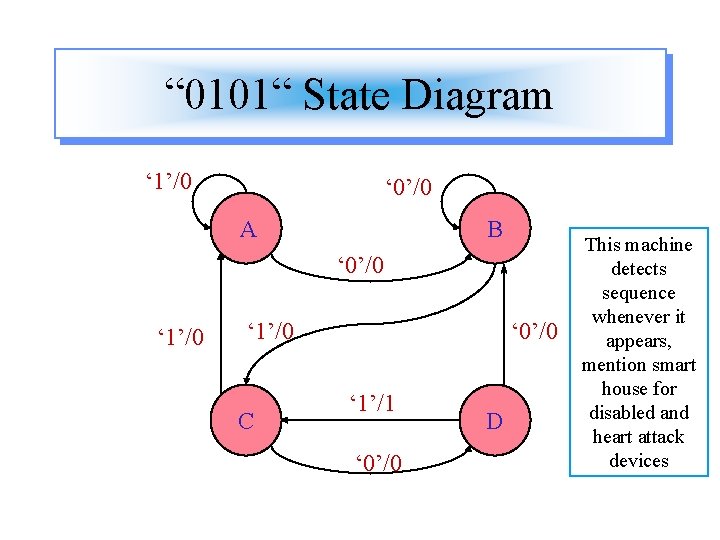
“ 0101“ State Diagram ‘ 1’/0 ‘ 0’/0 A B ‘ 0’/0 ‘ 1’/0 C ‘ 0’/0 ‘ 1’/1 ‘ 0’/0 D This machine detects sequence whenever it appears, mention smart house for disabled and heart attack devices

Moore “ 0101” Detector S: I: O: d: l: M = ( S, I, O, d, l ) { A, B, C, D, E } { ‘ 0’, ‘ 1’ } { 0, 1 } = { not detected, detected} next slide

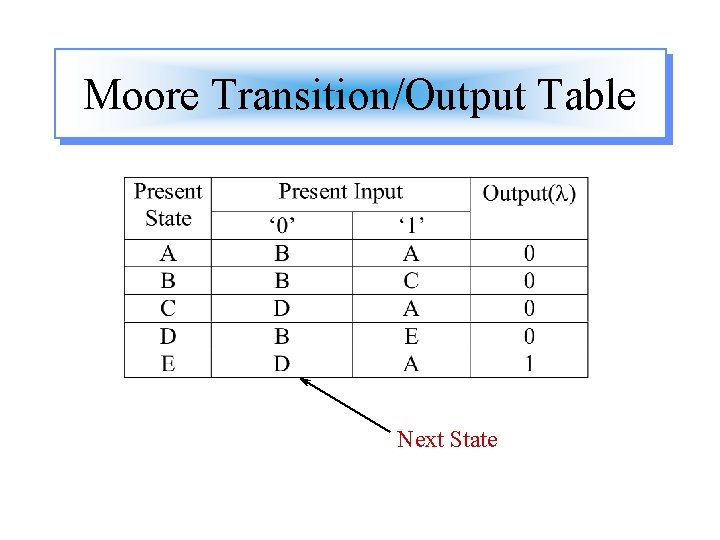
Moore Transition/Output Table Next State

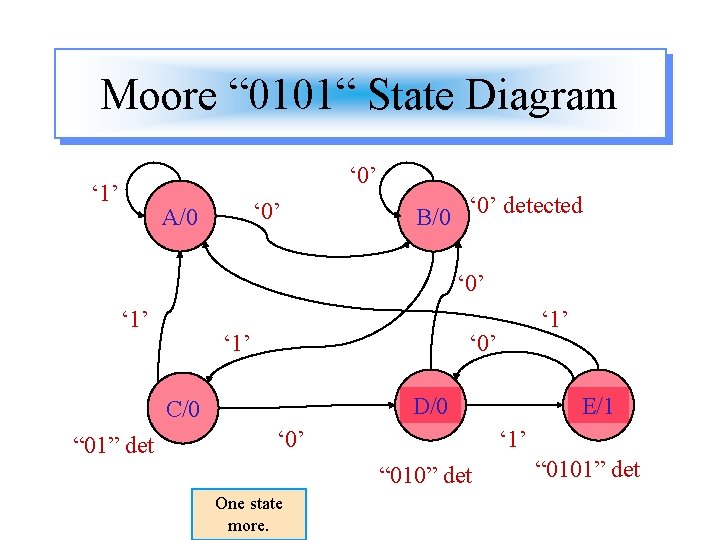
Moore “ 0101“ State Diagram ‘ 0’ ‘ 1’ ‘ 0’ A/0 B/0 ‘ 0’ detected ‘ 0’ ‘ 1’ ‘ 0’ D/0 C/0 “ 01” det ‘ 1’ ‘ 0’ ‘ 1’ “ 010” det One state more. E/1 “ 0101” det

Sequential Machines Problems Three Problems of Sequential Machines – State minimization problem • Determine all equivalent states of a sequential machine, and, • Eliminate redundant states – Machine Decomposition • Separate large machines into an interconnected set of smaller machines • Easier to design and analyze small machines Good but not always realistic advises: Instead to minimize, create minimal machine in first run. Instead to decompose, create decomposed machine in first run.

Sequential Machine Problems – State assignment problem • There is no guidance on which binary number to assign to which state in a primitive state table • Complexity of implementation is dependent on mapping of states to binary numbers • Unsolved problem – Design all machines and compare – Benefit of decomposition of large machine into smaller machines.

Set Theoretic Description Moore Machine is an ordered quintuple

Set Theoretic Description Mealy Machine is an ordered quintuple

Recursive Definitions of Delta State Transition for Moore & Mealy – Single-valued, else not deterministic. – At least a partial function – Not necessarily injective or surjective – Shield’s nomenclature

Recursive Definitions of Delta

Recursive Definitions of Beta • Causal, No Output for No Input. • For a Given Input Sequence, There Will Be a Deterministic Output Sequence of the Same Length As the Input.

Recursive Definitions of Lambda Same Caveats As Beta sk sk-1

Possible Exam Problems • Find if two state machines (of any type, Mealy, Moore or Rabin-Scott) describe the same regular language. • Find if a machine describes an empty language. • Find a regular language accepted by arbitrary type state machine, specified in any way (graph, table, etc. ). • Find the intersection, the union, the difference of two machines M 1 and M 2. • Find a negation of a machine M.

Possible Exam Problems • Find Mealy Machine for arbitrary sequence detection. • Find Moore Machine for arbitrary sequence detection, finite or infinite sequence over arbitrary alphabet. • Convert a Mealy Machine to an equivalent Moore Machine. • Convert a Moore Machine to an equivalent Mealy Machine.