Chapter 3 Regular Languages 1 3 1 Regular

Chapter 3 Regular Languages 1

3. 1: Regular Expressions (1) m m Regular Expression (RE): E is a regular expression over if E is one of: q q a, where a q If r and s are regular expressions (REs), then the following expressions also regular: Ø r | s (r or s) Ø rs (r followed by s) Ø r* (r repeated zero or more times) m Each RE has an equivalent regular language (RL) 2

3. 1: Regular Expressions (2) m m Regular Language (RL): L is a regular language over if L is one of: q empty set q { } a set that contains empty string q {a} where a q If R and S are regular languages (RL), then the following languages also regular: Ø R S = {w | w R or w S} Ø RS = {rs | r R and s S} Ø R* = R 0 R 1 R 2 R 3 … 3

3. 1: Regular Expressions (3) Rules for Specifying Regular Expressions: 1. is a regular expression L = { } 2. If a is in , a is a regular expression L = {a}, the set containing the string a. 3. Let r and s be regular expressions with languages L(r) and L(s). Then p r e c e d e n c e a. r | s is a RE L(r) L(s) b. rs is a RE L(r) L(s) c. r* is a RE (L(r))* d. (r) is a RE L(r), extra parenthesis 4

3. 1: Regular Expressions (4) m m Examples: q {0, 1}{00, 11} = {000, 011, 100, 111} q {0}* = { , 0, 000, 0000, …} q { }* = { } q {10, 01}* = { , 1010, 101010, …, 0101, 010101, …, 100101, 10010101, …, 011010, 01101010, …} Notational shorthand: q L 0 = { } q Li = LLi-1 q L+ = LL* 5

3. 1: Regular Expressions (5) m Let L be a language over {a, b}, each string in L contains the substring bb q L = {a, b}*{bb}{a, b}* m L is regular language (RL). Why? q {a} and {b} are RLs q {a, b} is RL q {a, b}* is RL q {b}{b} = {bb} is also RL q Then L = {a, b}*{bb}{a, b}* is RL 6

3. 1: Regular Expressions (6) m Let L be a language over {a, b}, each string in L q begins and ends with an a q contains at least one b q L = {a}{a, b}*{b}{a, b}*{a} m L is regular language (RL). Why? q {a} and {b} are RLs q {a, b} is RL q {a, b}* is RL q Then L = {a}{a, b}*{b}{a, b}*{a} is RL 7

3. 1: Regular Expressions (7) m L = {a, b}*{bb}{a, b}* q RE = (a|b)*bb(a|b)* m L = {a}{a, b}*{b}{a, b}*{a} q RE = a(a|b)*b(a|b)*a m This RE = (a)|((b)*(c)) is equivalent to a|b*c m We say REs r and s are equivalent (r=s), iff r and s represent the same language q Example: r = a|b, s = b|a r = s Why? q Since L(r) = L(s) = {a, b} 8

3. 1: Regular Expressions (8) m Let = {a, b} q q q q RE a|b RE (a|b) RE aa|ab|ba|bb RE a* RE (a|b)* RE (a*b*)* RE a|a*b L = {a, b} L = {aa, ab, ba, bb} same as above L = { , aa, aaa, …} L = set of all strings of a’s and b’s including same as above L = {a, b, aab, aaab, …} 9

3. 1: Regular Expressions (9) m Algebraic Properties of regular Expressions AXIOM r|s=s|r r | (s | t) = (r | s) | t (r s) t = r (s t) r(s|t)=rs|rt (s|t)r=sr|tr r=r =r r* = (r*)* = ( r | )+ = r+ | r** = r* r+ = r r* 10

3. 1: Regular Expressions (10) abc q concatenation (“followed by”) a|b|c q alternation (“or”) * q zero or more occurrences q one or more occurrences + 11

3. 1: Regular Expressions (11) m All strings of 1 s and 0 s (0 | 1)* m All strings of 1 s and 0 s beginning with a 1 1 (0 | 1)* 12

3. 1: Regular Expressions (12) m All strings containing two or more 0 s (1|0)*0(1|0)* m All strings containing an even number of 0 s (1*01*01*)* | 1* 13

3. 1: Regular Expressions (13) m All strings containing an even number of 0 s and even number of 1 s Assume that ( 0 0 | 1 1 ) is X X* | (X* ( 0 1 | 1 0 ) X*)* OR ( 0 0 | 1 1 )*(( 0 1 | 1 0 )( 0 0 | 1 1 )*)* m All strings of alternating 0 s and 1 s ( | 1 ) ( 0 1 )* ( | 0 ) 14

3. 1: Regular Expressions (14) m Strings over the alphabet {0, 1} with no consecutive 0's q (1 | 01 )* (0 | ) q 1*(01+)* (0 | ) q 1*(011*)* (0 | ) m Strings over the alphabet {a, b} with exactly three b's q a*ba*ba*ba* m Strings over the alphabet {a, b, c} containing (at least once) bc q (a|b|c)*bc(a|b|c)* 15

3. 1: Regular Expressions (15) m Strings over the alphabet {a, b} in which substrings ab and ba occur an unequal number of times q (a+b+)+ | (b+a+)+ 16

3. 1: Regular Expressions (16) m Describe the following in English: q (0|1)* Ø all strings over {0, 1} q b*ab*ab*ab* Ø all strings over {a, b} with exactly 3 a’s 17

3. 1: Regular Expressions (17) m Examples of RE: q 01* Ø {0, 011, 0111, …. . } q (01*)(01) Ø {001, 01101, 011101, …. . } q (0 | 1)* = {0, 1, 00, 01, 10, 11, …. . } Ø i. e. , all strings of 0 and 1 q (0 | 1)* 00 (0 | 1)* = {00, 1001, …. . } Ø i. e. , all 0 and 1 strings containing a “ 00” 18

3. 1: Regular Expressions (18) m More Examples of RE: q (1 | 10)* Ø all strings starting with “ 1” and containing no “ 00” q (0 | 1)*011 Ø all strings ending with “ 011” q 0*1* Ø all strings with no “ 0” after “ 1” q 00*11* Ø all strings with at least one “ 0” and one “ 1”, and no “ 0” after “ 1” 19

3. 1: Regular Expressions (19) m What languages do the following RE represent? q ((0 | 1))* | ((0 | 1)(0 | 1))* 20

3. 1: Regular Expressions (20) m Home Study: q Construct a RE over ={0, 1} such that Ø It does not contain any string with two consecutive “ 0”s Ø It has no prefix with two or more “ 0”s than “ 1” nor two or more “ 1”s than “ 0” Ø The set of all strings ending with “ 00” Ø The set of all strings with 3 consecutive 0’s Ø The set of all strings beginning with “ 1”, which when interpreted as a binary no. , is divisible by 5 Ø The set of all strings with a “ 1” at the 5 th position from the right Ø The set of all strings not containing 101 as a sub-string 21

3. 2: Connection Between RE & RL (1) m A language L is called regular if and only if there exists some DFA M such that L = L(M). m Since a DFA has an equivalent NFA, then q A language L is called regular if and only if there exists some NFA N such that L = L(N). m If we have a RE r, we can construct an NFA that accept L(r). 22

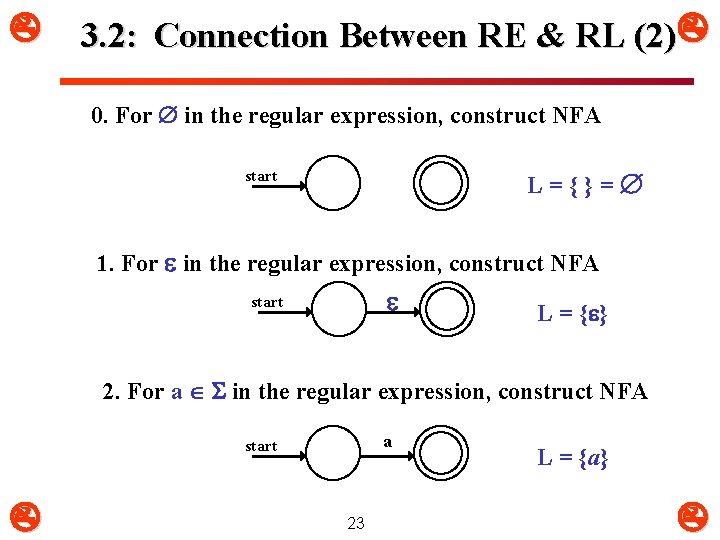
3. 2: Connection Between RE & RL (2) 0. For in the regular expression, construct NFA L={}= start 1. For in the regular expression, construct NFA start L = { } 2. For a in the regular expression, construct NFA a start 23 L = {a}

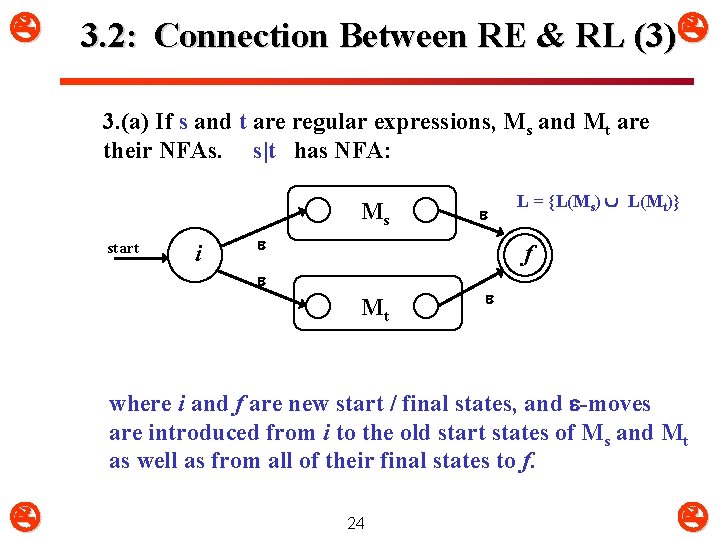
3. 2: Connection Between RE & RL (3) 3. (a) If s and t are regular expressions, Ms and Mt are their NFAs. s|t has NFA: Ms start i L = {L(Ms) L(Mt)} f Mt where i and f are new start / final states, and -moves are introduced from i to the old start states of Ms and Mt as well as from all of their final states to f. 24

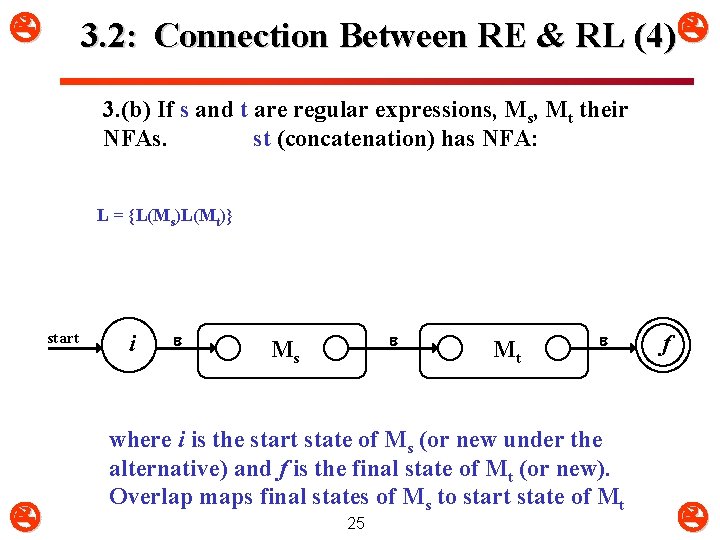
3. 2: Connection Between RE & RL (4) 3. (b) If s and t are regular expressions, Mt their NFAs. st (concatenation) has NFA: L = {L(Ms)L(Mt)} start i Ms Mt where i is the start state of Ms (or new under the alternative) and f is the final state of Mt (or new). Overlap maps final states of Ms to start state of Mt 25 f

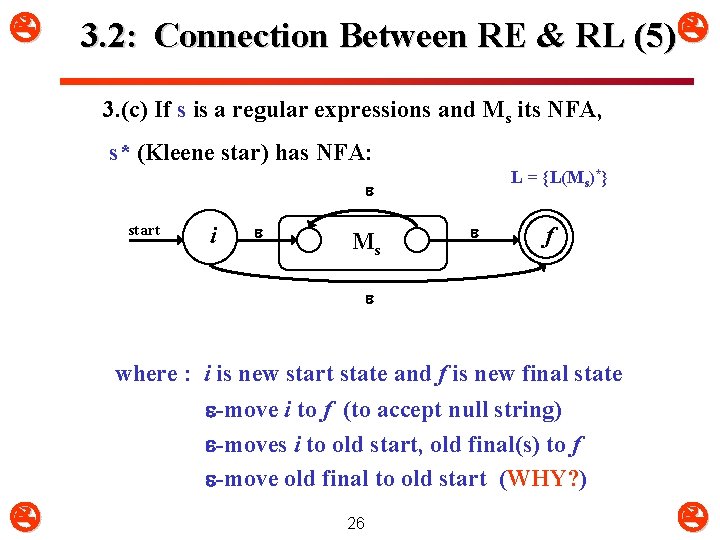
3. 2: Connection Between RE & RL (5) 3. (c) If s is a regular expressions and Ms its NFA, s* (Kleene star) has NFA: L = {L(Ms)*} start i Ms f where : i is new start state and f is new final state -move i to f (to accept null string) -moves i to old start, old final(s) to f -move old final to old start (WHY? ) 26

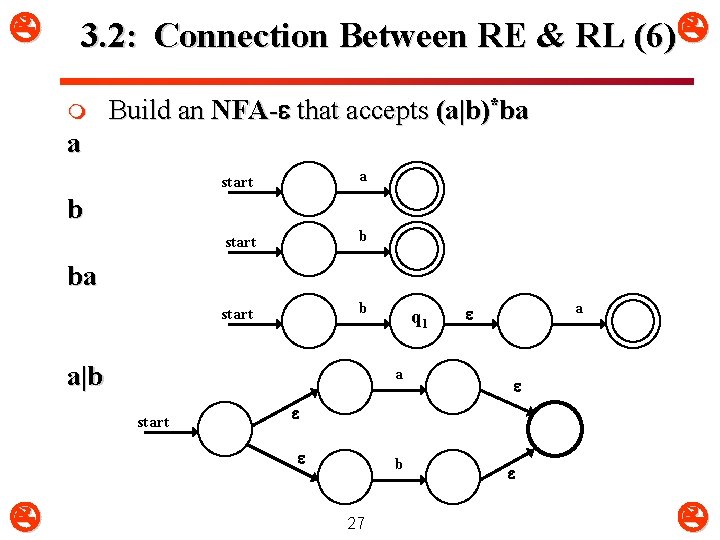
3. 2: Connection Between RE & RL (6) m Build an NFA- that accepts (a|b)*ba a start b b ba a|b a start a q 1 b 27

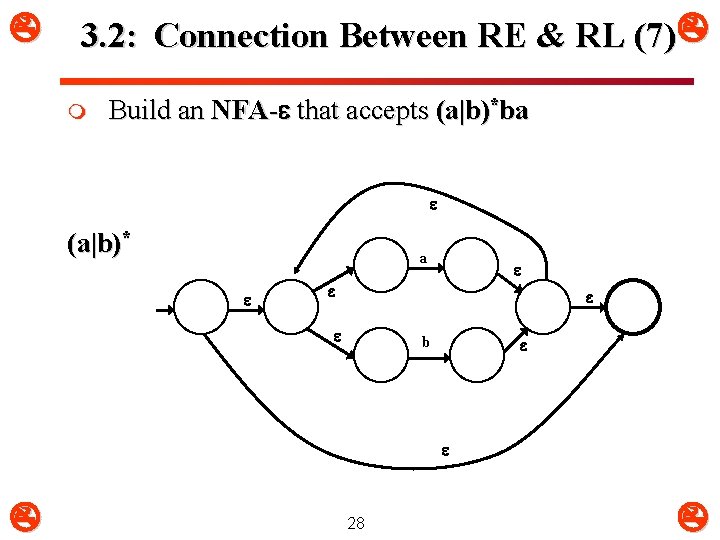
3. 2: Connection Between RE & RL (7) m Build an NFA- that accepts (a|b)*ba (a|b)* a b 28

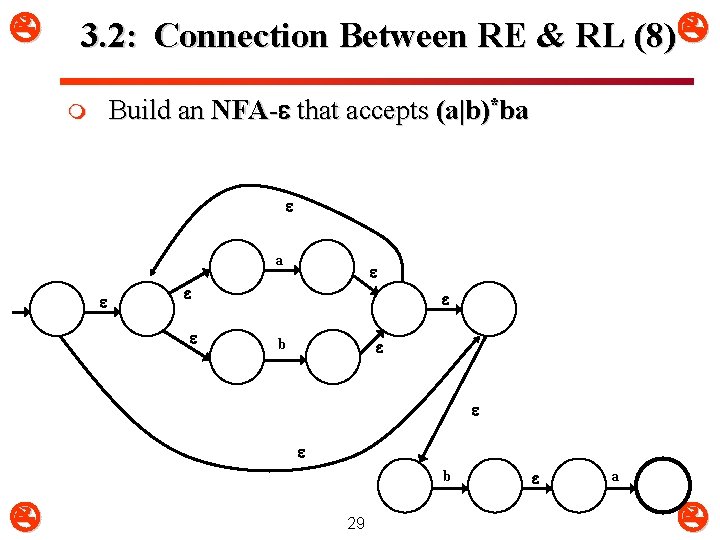
3. 2: Connection Between RE & RL (8) Build an NFA- that accepts (a|b)*ba m a b 29 a

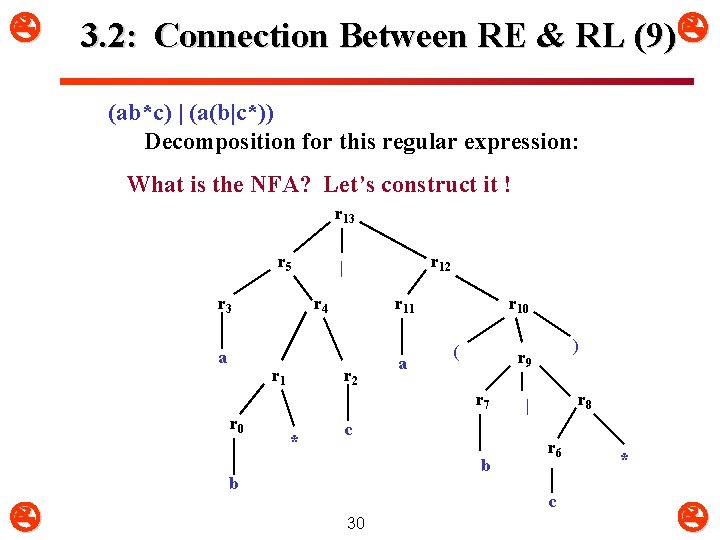
3. 2: Connection Between RE & RL (9) (ab*c) | (a(b|c*)) Decomposition for this regular expression: What is the NFA? Let’s construct it ! r 13 r 5 r 3 a r 12 | r 4 r 11 r 2 a r 10 ( r 7 r 0 * c b b ) r 9 r 8 | r 6 c 30 *

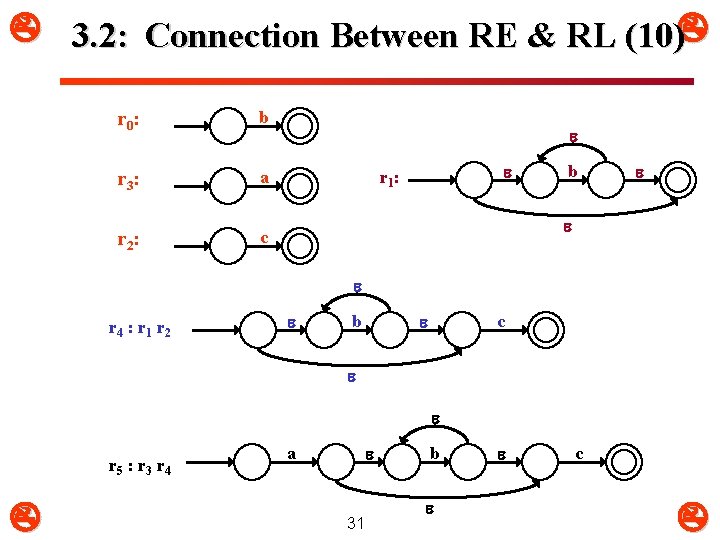
3. 2: Connection Between RE & RL (10) r 0 : b r 3 : a r 2 : c r 1 : b r 4 : r 1 r 2 b c r 5 : r 3 r 4 a 31 b c

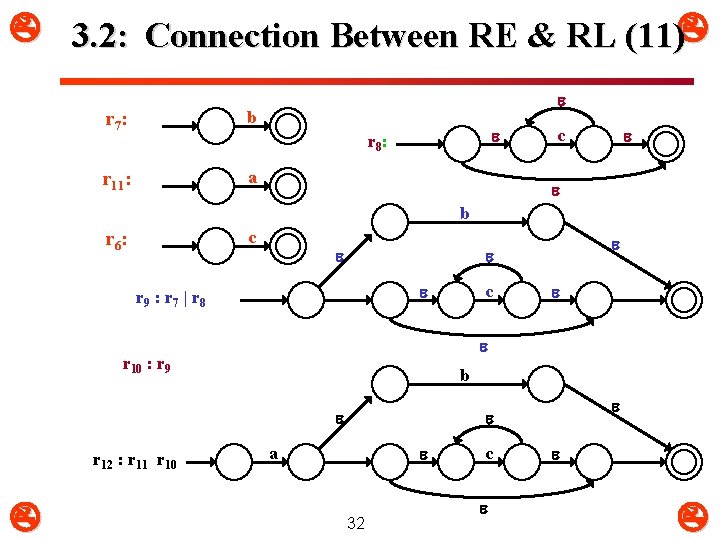
3. 2: Connection Between RE & RL (11) r 7 : b r 11: a r 8 : c b c r 6 : r 9 : r 7 | r 8 b c r 10 : r 9 r 12 : r 11 r 10 a 32 c

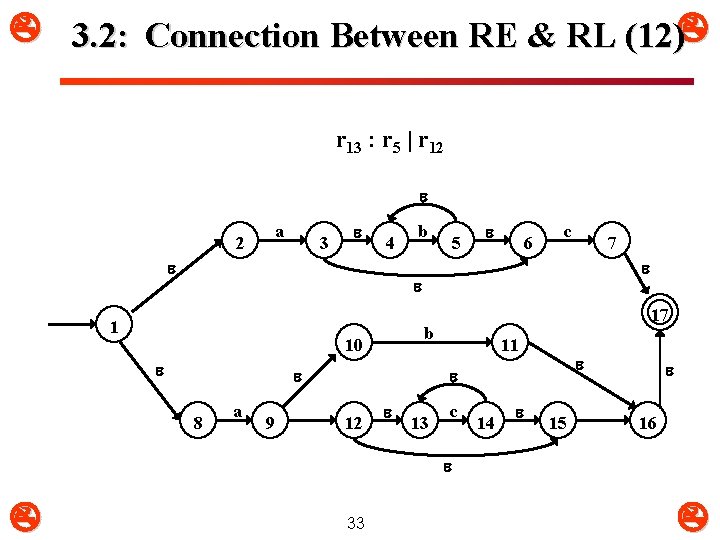
3. 2: Connection Between RE & RL (12) r 13 : r 5 | r 12 a 2 3 4 b 5 6 c 7 1 b 10 8 a 9 17 11 12 13 c 14 15 16 33

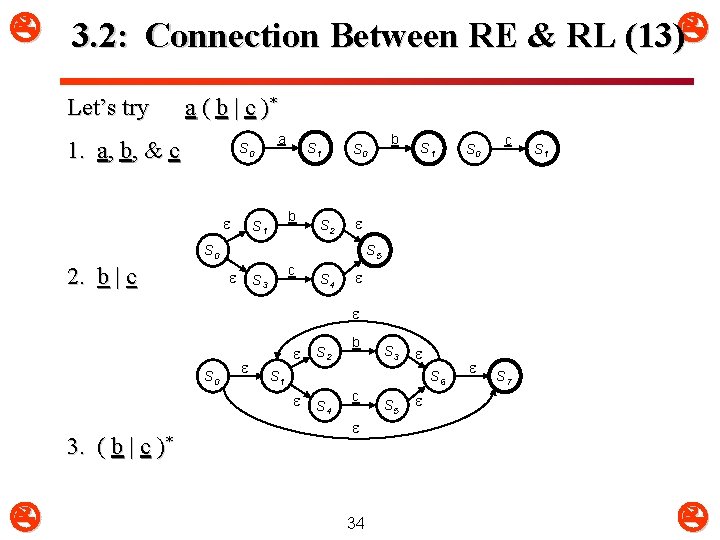
3. 2: Connection Between RE & RL (13) Let’s try a ( b | c )* 1. a, b, & c S 0 a S 1 b S 1 S 2 S 0 S 1 S 0 c S 1 S 0 2. b | c b S 5 c S 3 S 4 S 0 3. ( b | c b S 3 S 1 S 6 )* S 2 S 4 c S 5 S 7 34

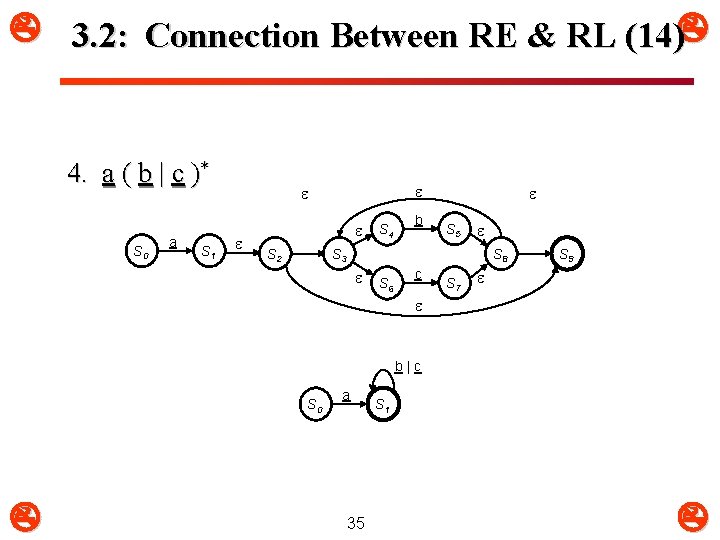
3. 2: Connection Between RE & RL (14) 4. a ( b | c )* S 0 a S 1 S 2 S 4 b S 5 S 3 S 8 S 6 c S 7 S 9 b|c S 0 a 35 S 1

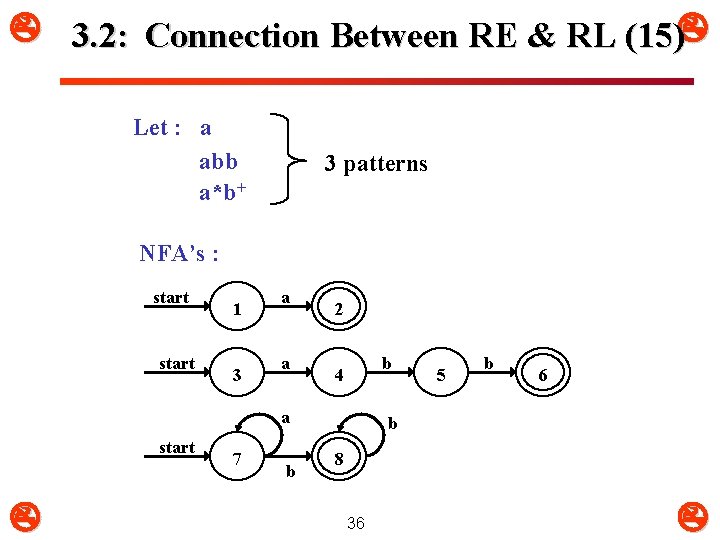
3. 2: Connection Between RE & RL (15) Let : a abb a*b+ 3 patterns NFA’s : start 1 3 a a 2 b 4 a start 7 b 5 b 6 b 8 36

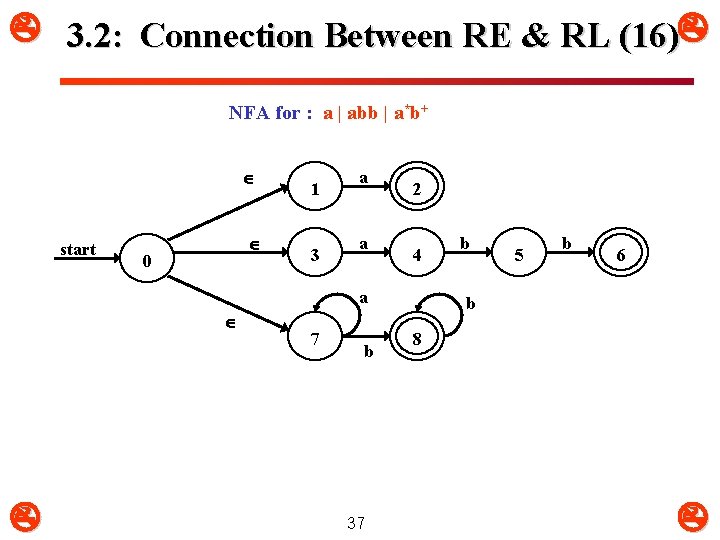
3. 2: Connection Between RE & RL (16) NFA for : a | abb | a*b+ start 0 1 3 a a 2 4 a 7 b 37 b 5 b 6 b 8

Regular Expression to NFA- (a | ba)*a 38

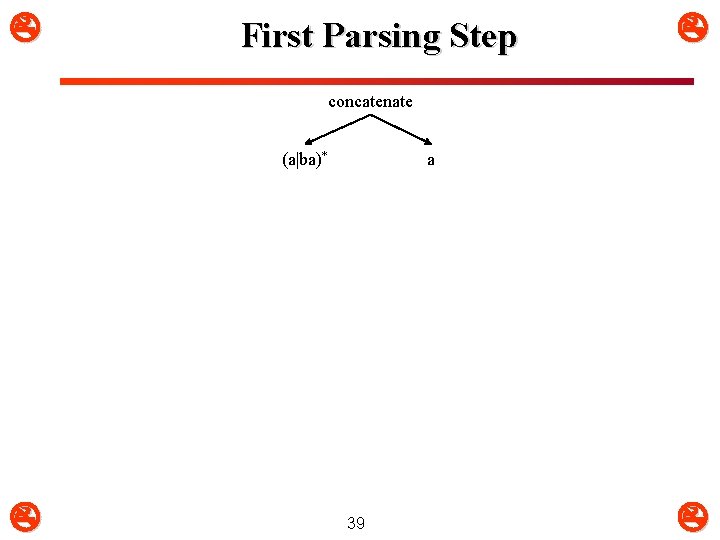
First Parsing Step concatenate (a|ba)* a 39

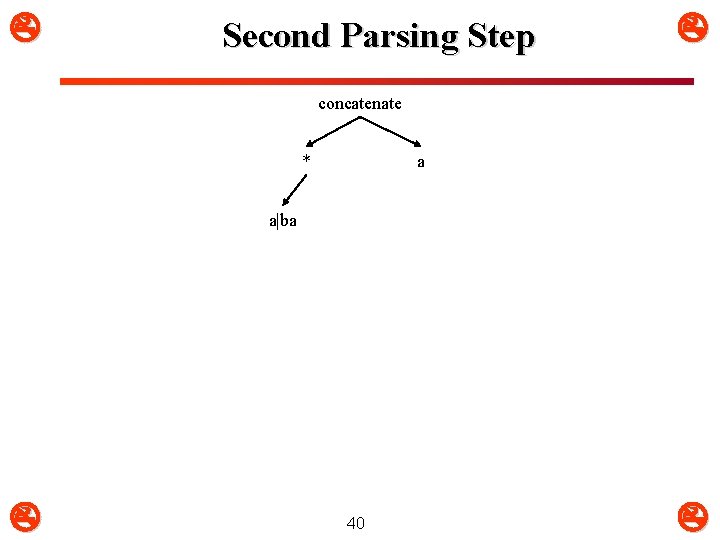
Second Parsing Step concatenate * a a|ba 40

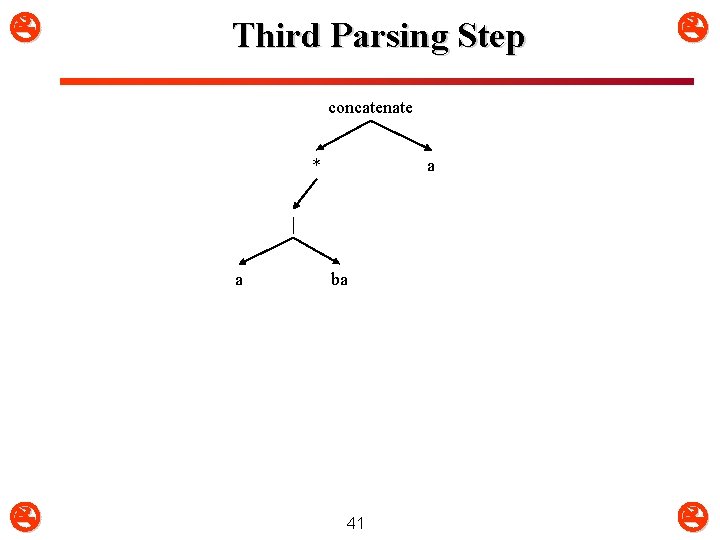
Third Parsing Step concatenate * a | a ba 41

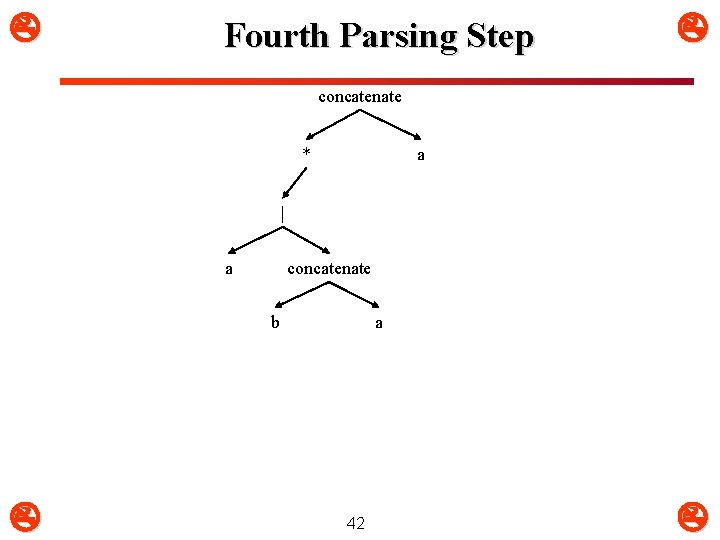
Fourth Parsing Step concatenate * a | a concatenate b a 42

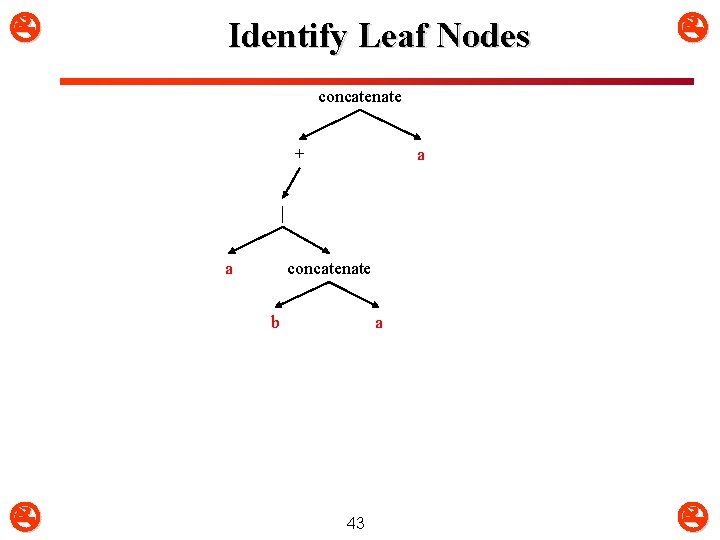
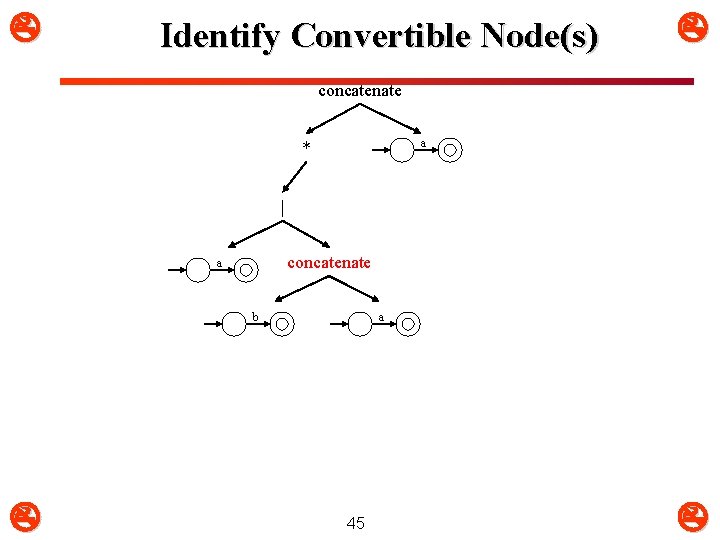
Identify Leaf Nodes concatenate + a | a concatenate b a 43

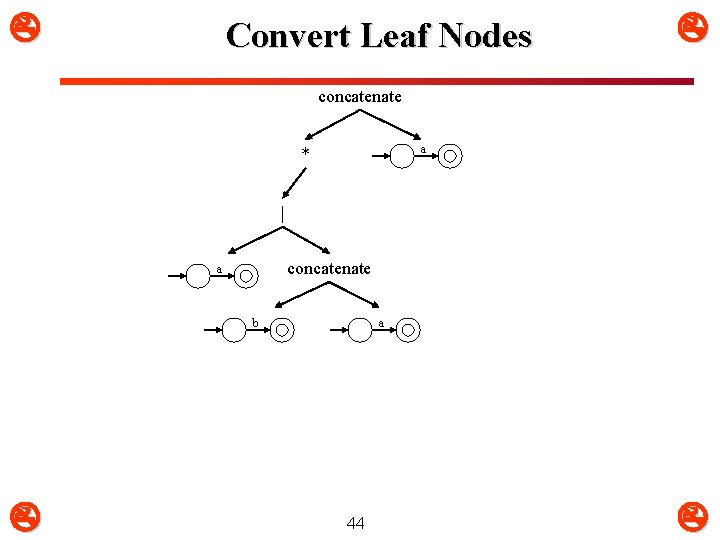
Convert Leaf Nodes concatenate a * | concatenate a b a 44

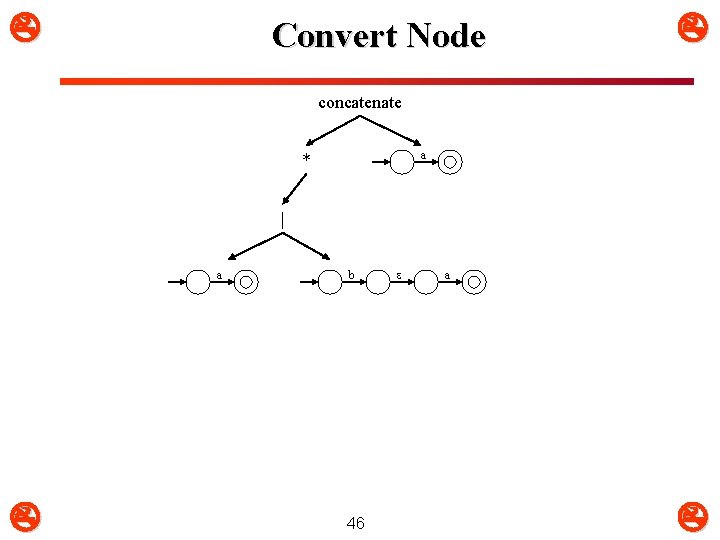
Identify Convertible Node(s) concatenate a * | concatenate a b a 45

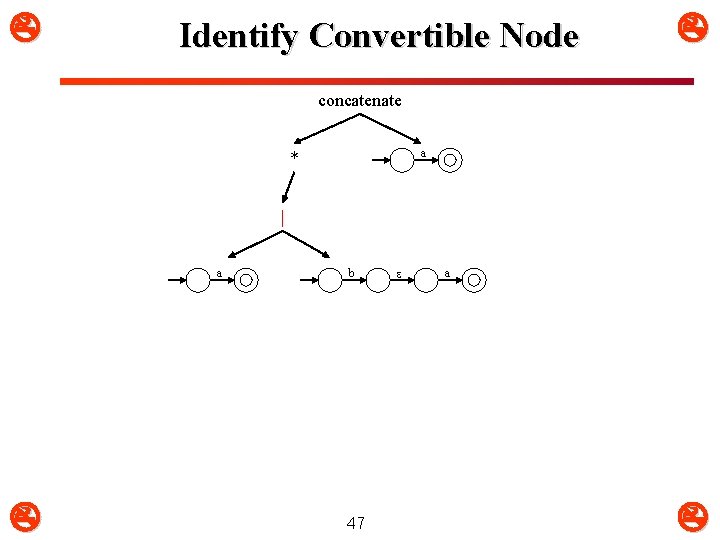
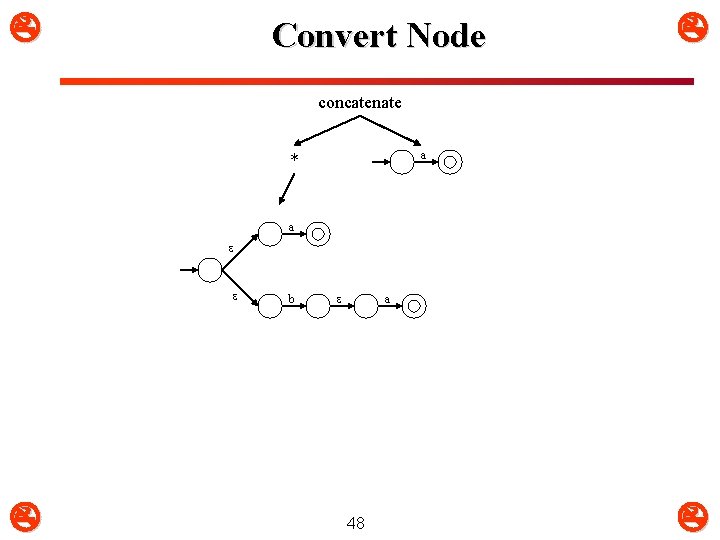
Convert Node concatenate a * | a b 46 a

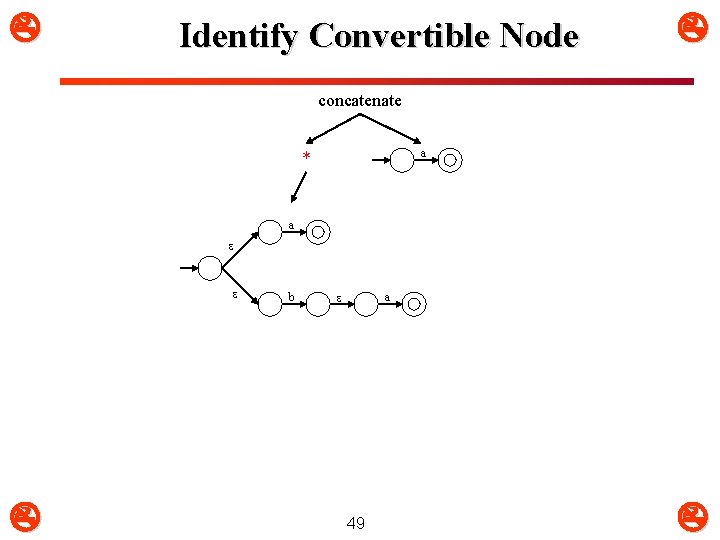
Identify Convertible Node concatenate a * | a b 47 a

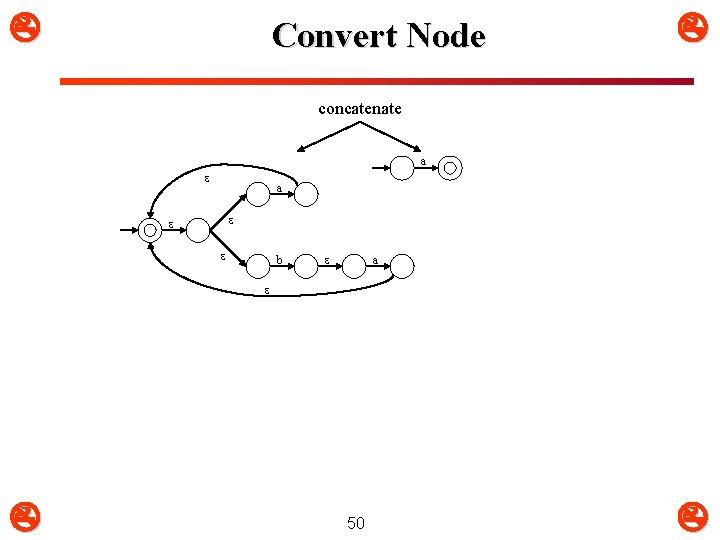
Convert Node concatenate a * a b a 48

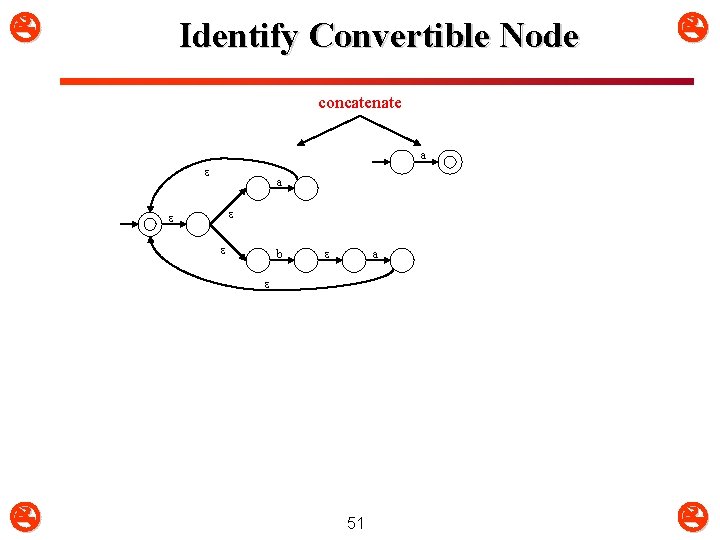
Identify Convertible Node concatenate a * a b a 49

Convert Node concatenate a a b a 50

Identify Convertible Node concatenate a a b a 51

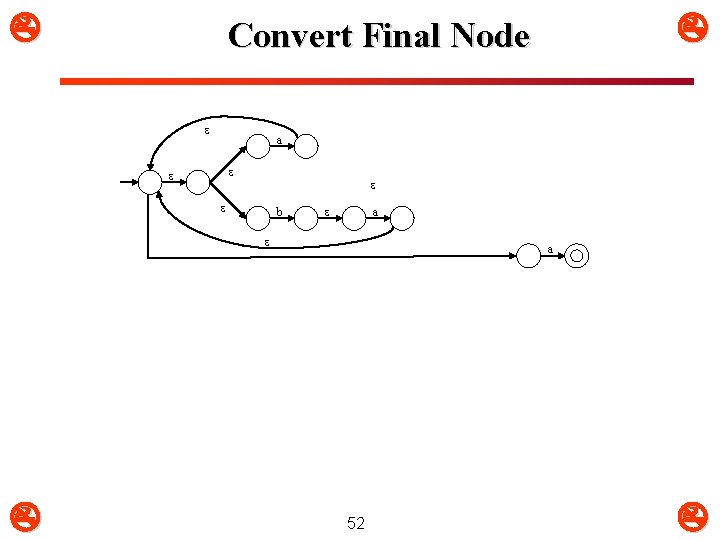
a b a Convert Final Node a 52

3. 2: Expression Graphs (1) m NFA to RE m If L is accepted by some NFA- , then L is represented by some regular expression An expression graph is like a state diagram but it can have regular expressions as labels on arcs An NFA- is an expression graph An expression graph can be reduced to one with just two states If we reduce an NFA- in this way, the arc label then corresponds to the regular expression representing it m m 53

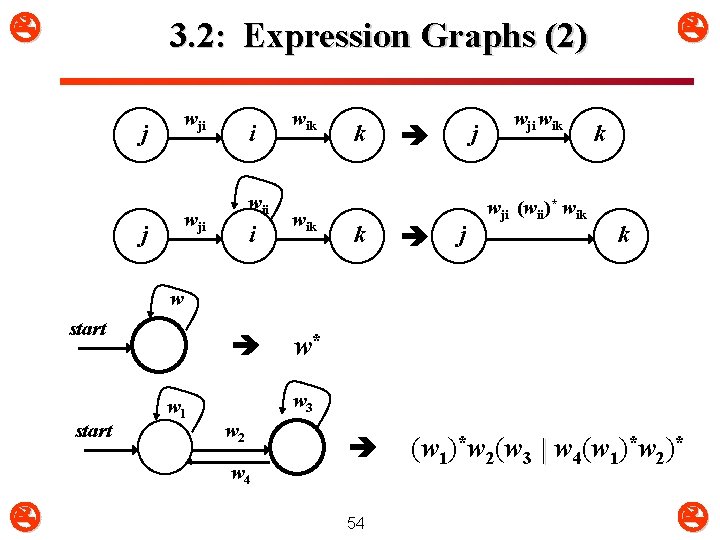
3. 2: Expression Graphs (2) wji j i wii wji j i wik k k j j wji wik wji (wii)* wik k k w start w 1 w 3 w 2 w 4 w* 54 (w 1)*w 2(w 3 | w 4(w 1)*w 2)*

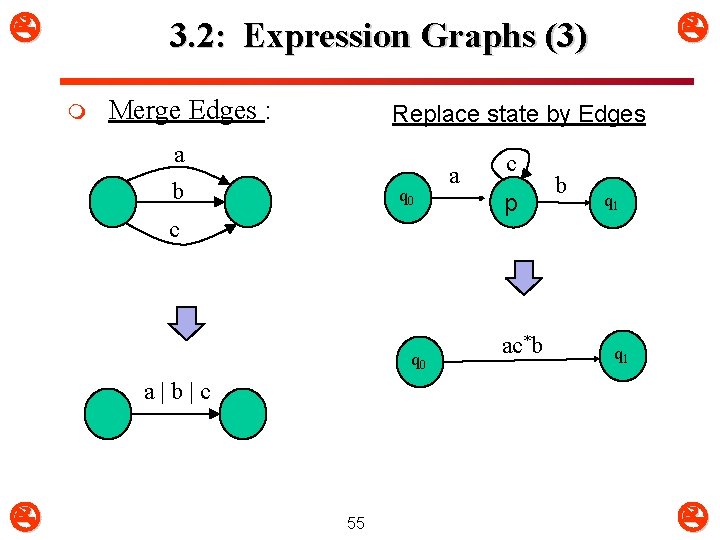
3. 2: Expression Graphs (3) m Merge Edges : Replace state by Edges a b q 0 c q 0 a c p ac*b b q 1 a|b|c 55

3. 2: Expression Graphs (4) m m m Let G be the state diagram of a finite automata Let m be the number of final states of G Make m copies of G, each of which has one final state. Call these graphs G 1, G 2, …, Gm For each Gt q Repeat Ø Do the steps in the previous slide Until the only states in Gt are the start state and the single final state q Determine the RE of Gt The RE of G is obtained by joining RE’s of each Gt by or | q m 56

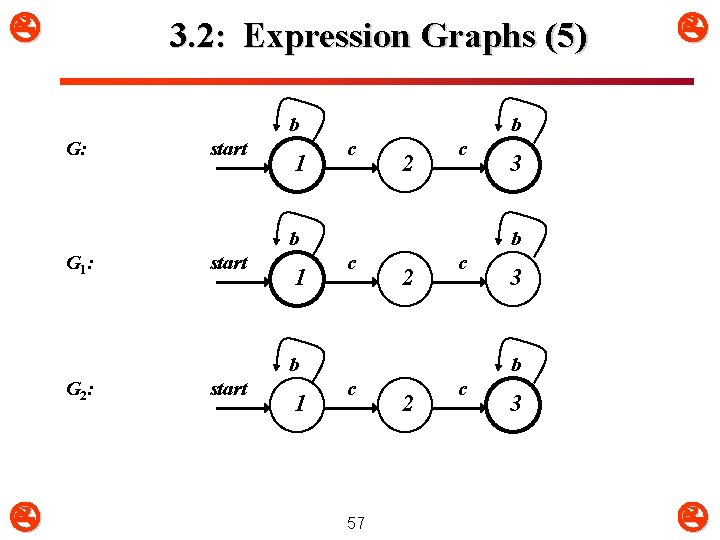
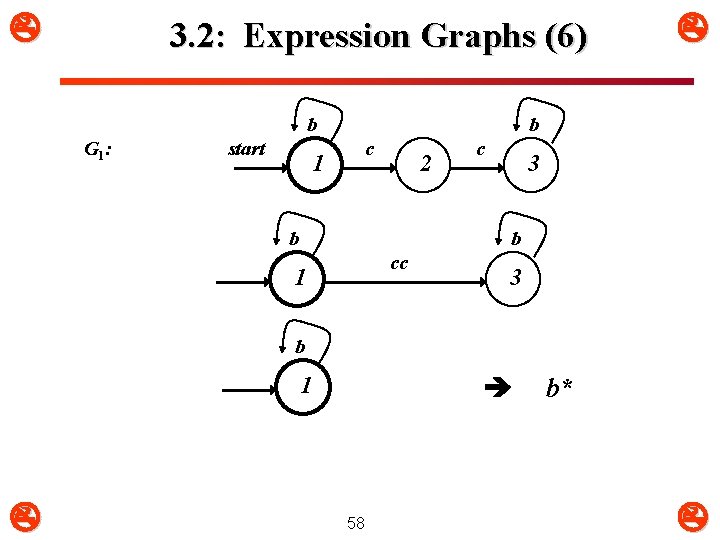
3. 2: Expression Graphs (5) b G: start 1 b c 2 c b G 1 : start 1 3 b c 2 c b G 2 : 3 b c 57 2 c 3

3. 2: Expression Graphs (6) b G 1 : start 1 b c 2 b c 3 b cc 1 3 b 1 58 b*

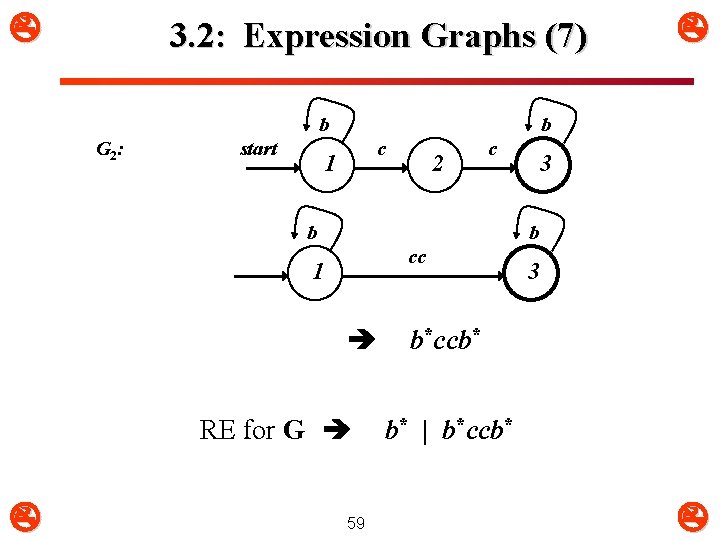
3. 2: Expression Graphs (7) b G 2 : start b c 1 2 c b 3 b cc 1 RE for G 59 3 b*ccb* b* | b*ccb*