Why are random matrix eigenvalues cool Alan Edelman

Why are random matrix eigenvalues cool? Alan Edelman MIT: Dept of Mathematics, Lab for Computer Science MAA Mathfest 2002 Thursday, August 1 10/18/2021 1

Message v v v Ingredient: Take Any important mathematics Then Randomize! This will have many applications! 10/18/2021 2

Some fun tidbits The circular law v The semi-circular law v Infinite vs finite v How many are real? v Stochastic Numerical Algorithms v Condition Numbers v Small networks v Riemann Zeta Function v Matrix Jacobians v 10/18/2021 3

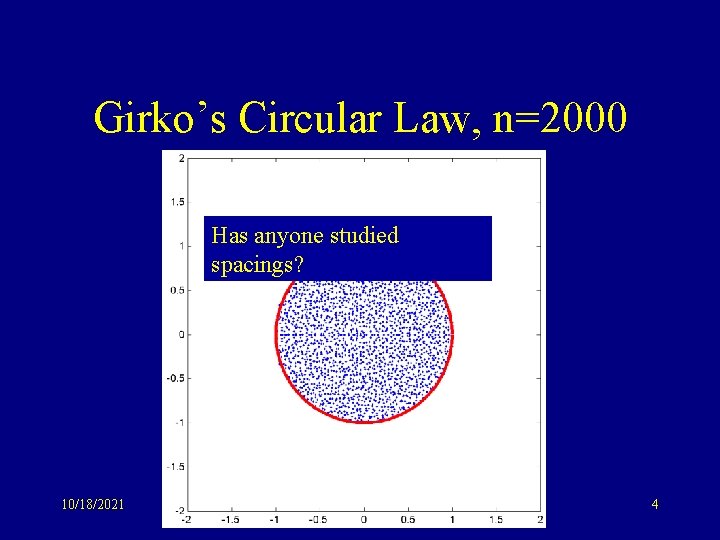
Girko’s Circular Law, n=2000 Has anyone studied spacings? 10/18/2021 4

Wigner’s Semi-Circle v The classical & most famous rand eig v Let S = random symmetric Gaussian v MATLAB: v Normalized v Precise theorem A=randn(n); S=(A+A’)/2; eigenvalue histogram is a semi-circle statements require n etc. n=20; s=30000; d=. 05; %matrix size, samples, sample dist e=[]; %gather up eigenvalues im=1; %imaginary(1) or real(0) for i=1: s, a=randn(n)+im*sqrt(-1)*randn(n); a=(a+a')/(2*sqrt(2*n*(im+1))); v=eig(a)'; e=[e v]; end hold off; [m x]=hist(e, -1. 5: d: 1. 5); bar(x, m*pi/(2*d*n*s)); axis('square'); axis([-1. 5 -1 2]); hold on; t=-1: . 01: 1; plot(t, sqrt(1 -t. ^2), 'r'); 6

Elements of Wigner’s Proof v Compute E(A 2 k)11= mean( 2 k) = (2 k)th moment v Verify that the semicircle is the only distribution with these moments v (A 2 k)11 = A 1 x. Axy…Awz. Az 1 “paths” of length 2 k v Need only count number of special paths of length 2 k on k objects (all other terms 0 or negligible!) v This is a Catalan Number! 10/18/2021 7

Catalan Numbers =# ways to “parenthesize” (n+1) objects Matrix Power Term Graph (1((23)4)) A 12 A 23 A 32 A 24 A 42 A 21 (((12)3)4) A 12 A 21 A 13 A 31 A 14 A 41 (1(2(34))) A 12 A 23 A 34 A 43 A 32 A 21 ((12)(34)) A 12 A 21 A 13 A 34 A 43 A 31 ((1(23))4) A 12 A 23 A 32 A 21 A 14 A 41 = number of special paths on n departing from 1 once v Pass 1, (load=advance, multiply=retreat), Return to 1 10/18/2021 8

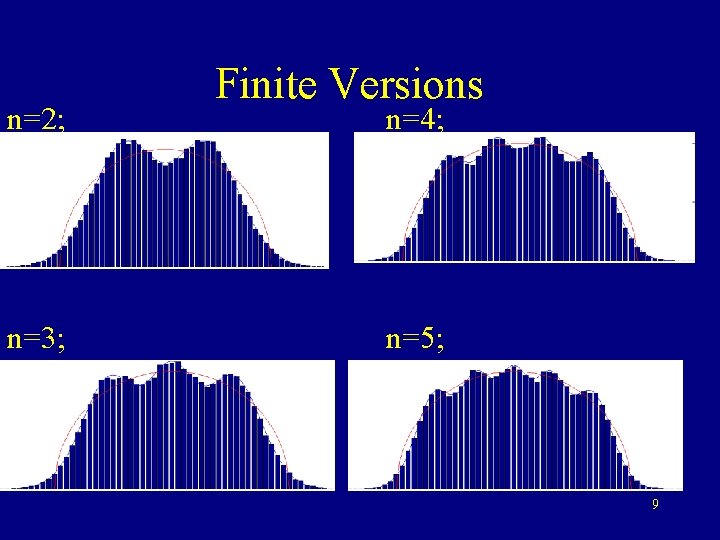
n=2; n=3; Finite Versions n=4; n=5; 9

How many eigenvalues of a random matrix are real? >> e=eig(randn(7)) e= 1. 9771 1. 3442 0. 6316 -1. 1664 + 1. 3504 i -1. 1664 - 1. 3504 i -2. 1461 + 0. 7288 i -2. 1461 - 0. 7288 i 3 real >> e=eig(randn(7)) e= -2. 0767 + 1. 1992 i -2. 0767 - 1. 1992 i 2. 9437 0. 0234 + 0. 4845 i 0. 0234 - 0. 4845 i 1. 1914 + 0. 3629 i 1. 1914 - 0. 3629 i 1 real >> e=eig(randn(7)) e= -2. 1633 -0. 9264 -0. 3283 2. 5242 1. 6230 + 0. 9011 i 1. 6230 - 0. 9011 i 0. 5467 5 real 7 x 7 random Gaussian 10/18/2021 10

How many eigenvalues of a random matrix are real? n=7 7 reals 0. 00069 5 reals 0. 08460 3 reals 0. 57727 These are 1 exact 0. 33744 real but hard to compute! New research suggests a Jack polynomial solution. 10/18/2021 12

How many eigenvalues of a random matrix are real? v The Probability that a matrix has all real eigenvalues is exactly -n(n-1)/4 Pn, n=2 Proof based on Schur Form 10/18/2021 13

Gram Schmidt (or QR) Stochastically • Gram Schmidt = Orthogonal Transformations to Upper Triangular Form • A = Q * R (orthog * upper triangular) 10/18/2021 14

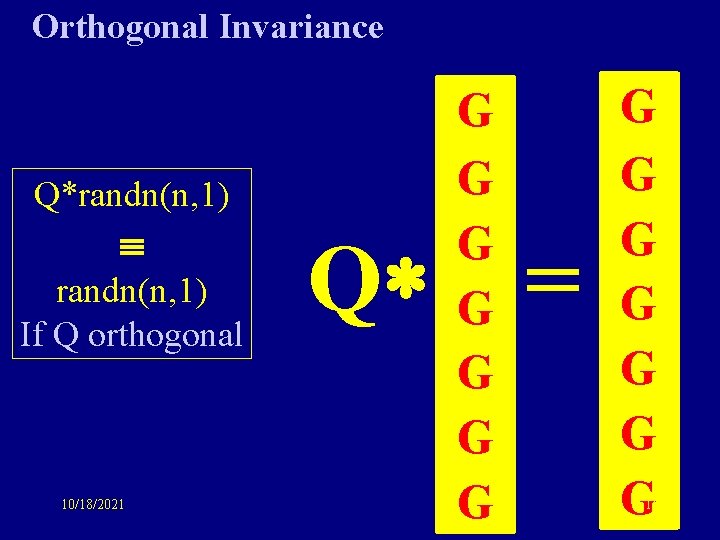
Orthogonal Invariance of Gaussians Q*randn(n, 1) If Q orthogonal 10/18/2021 Q G G G G 15

Orthogonal Invariance Q*randn(n, 1) If Q orthogonal 10/18/2021 G G G G Q = G G G G 16

Chi Distribution norm(randn(n, 1)) n 10/18/2021 G G G G = n 17

Chi Distribution norm(randn(n, 1)) n 10/18/2021 G G G G = n 18

Chi Distribution norm(randn(n, 1)) n n need not be integer 10/18/2021 G G G G = n 19

10/18/2021 G G G G G G G G G G G G G 20

10/18/2021 G G G G G G G G G G G G G 21

10/18/2021 7 O O O G G G G G G G G G G G 22

10/18/2021 7 O O O G G G G G G G G G G G 23

10/18/2021 7 O O O G G G G G G G G G G G 24

10/18/2021 7 O O O G G G G G G G G G G G 25

10/18/2021 7 O O O G G G G G G G G G G G 26

10/18/2021 7 O O O G G G G G G G G G G G 27

10/18/2021 7 O O O G G G G G G G G G G G 28

10/18/2021 7 O O O G G G G G G G G G G G 29

10/18/2021 7 O O O G G G G G G G G G G G 30

10/18/2021 7 O O O G G G G G G G G G G G 31

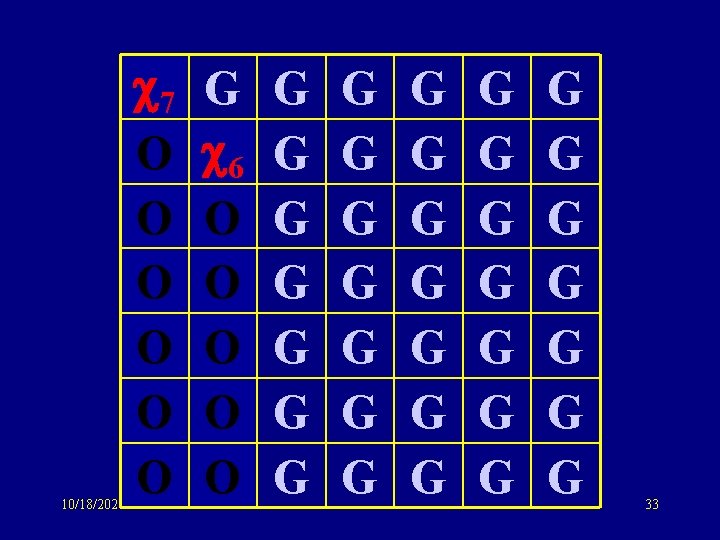
10/18/2021 7 O O O G 6 O O O G G G G G G G G G 32

10/18/2021 7 O O O G 6 O O O G G G G G G G G G 33

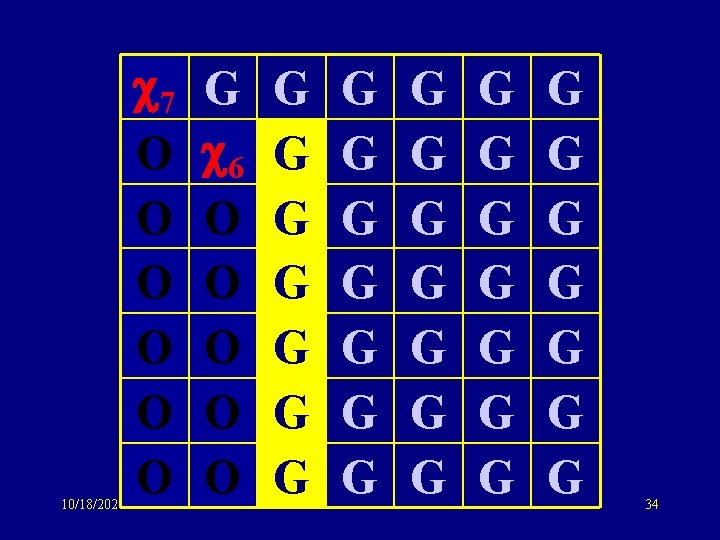
10/18/2021 7 O O O G 6 O O O G G G G G G G G G 34

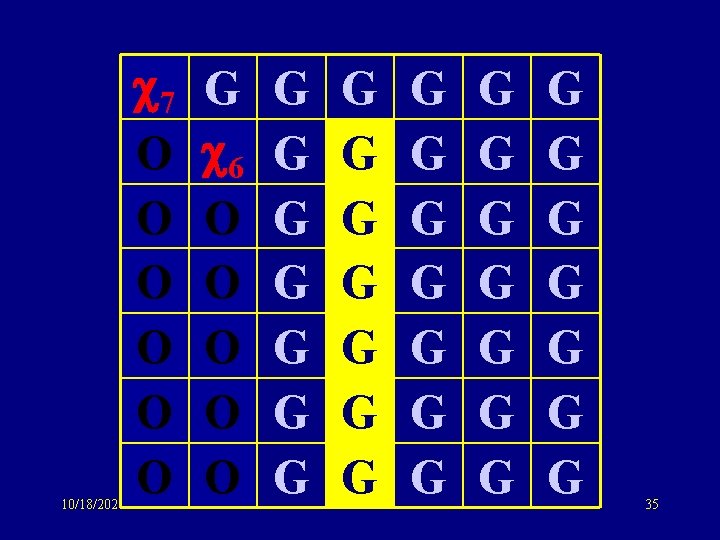
10/18/2021 7 O O O G 6 O O O G G G G G G G G G 35

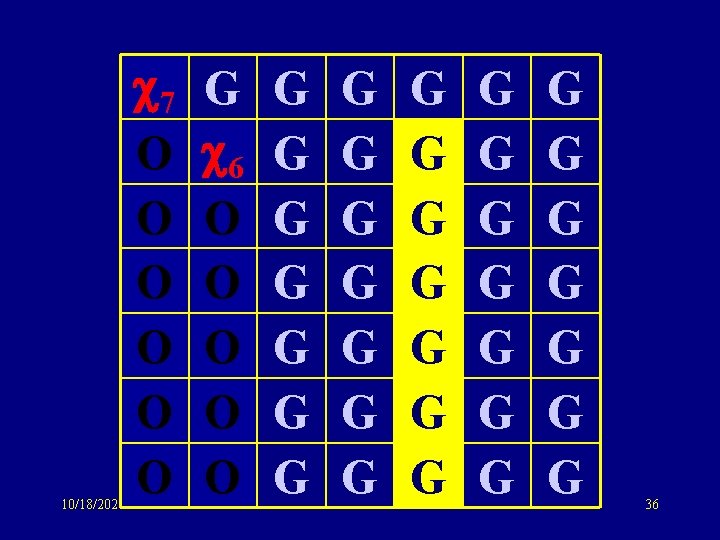
10/18/2021 7 O O O G 6 O O O G G G G G G G G G 36

10/18/2021 7 O O O G 6 O O O G G G G G G G G G 37

10/18/2021 7 O O O G 6 O O O G G G G G G G G G 38

10/18/2021 7 O O O G 6 O O O G G G G G G G G G 39

10/18/2021 7 O O O G 6 O O O G G G G G G G G G 40

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 41

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 42

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 43

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 44

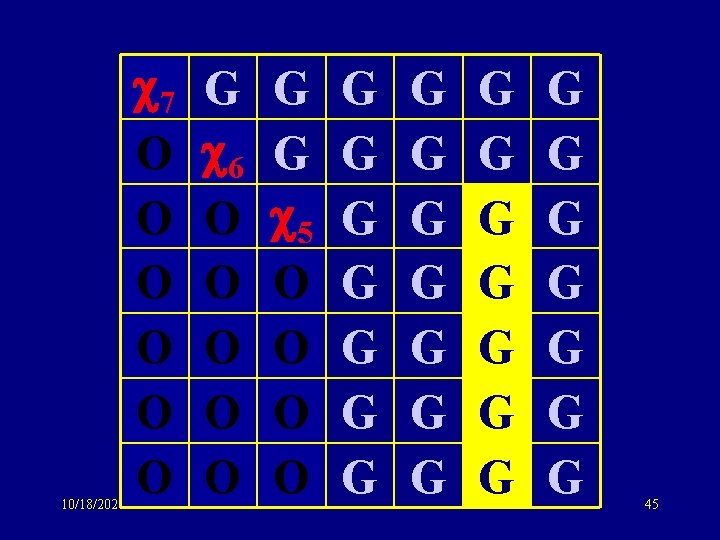
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 45

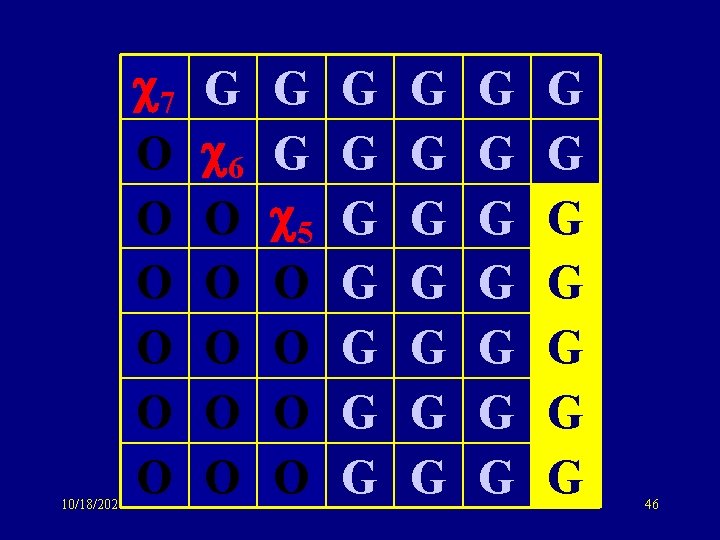
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 46

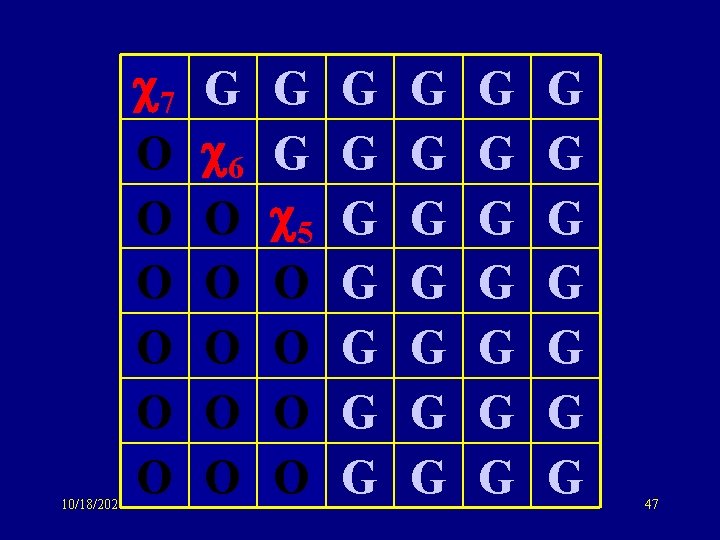
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 47

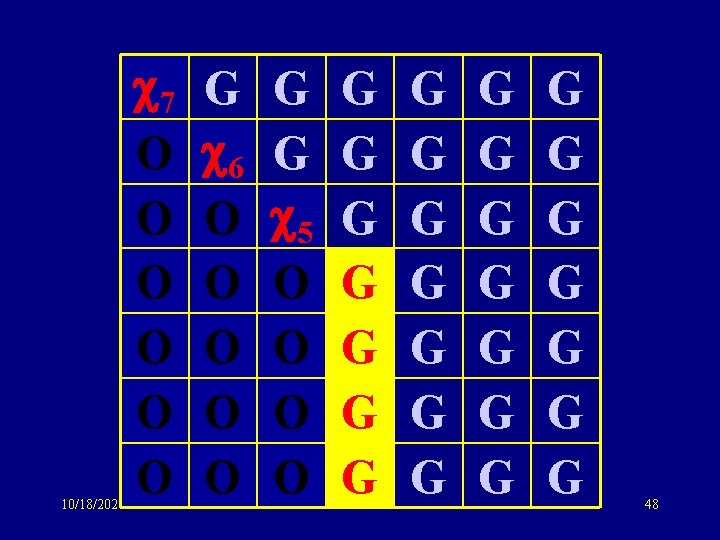
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G G G G G 48

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 49

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 50

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 51

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 52

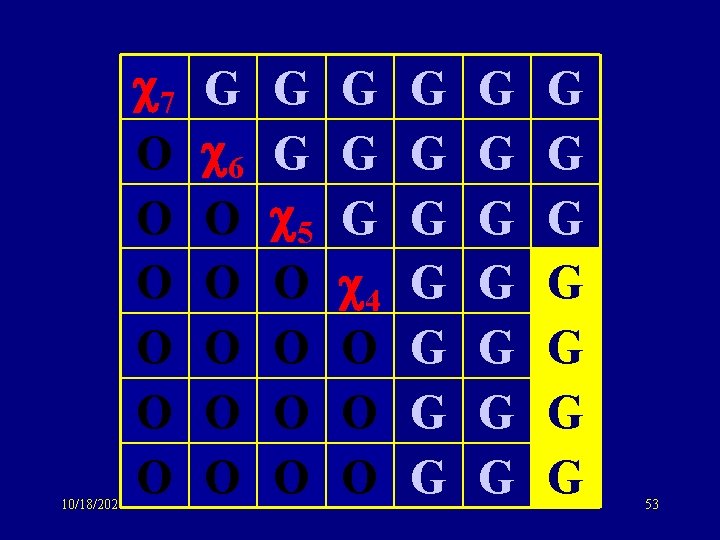
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 53

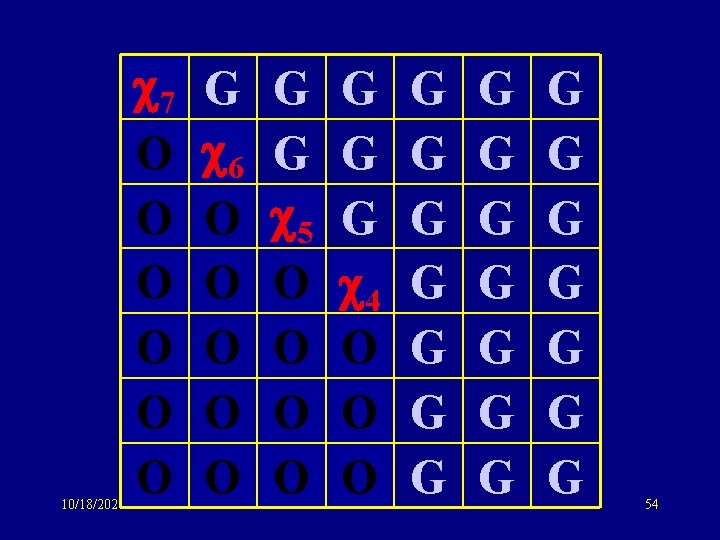
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 54

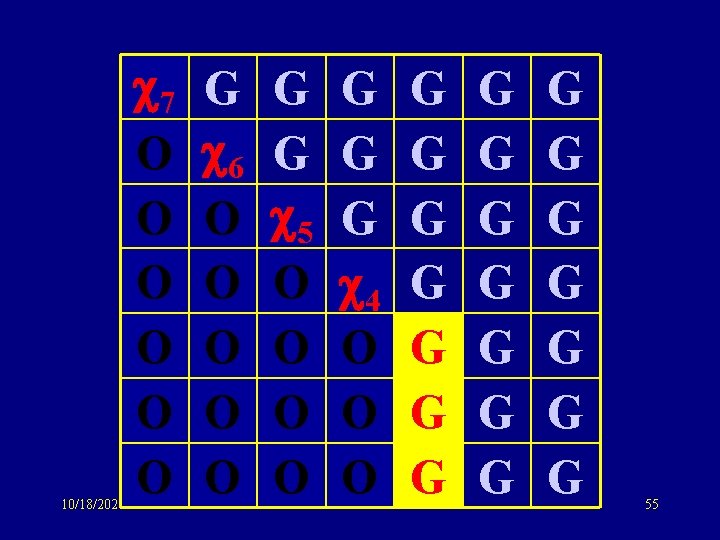
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G G G G G 55

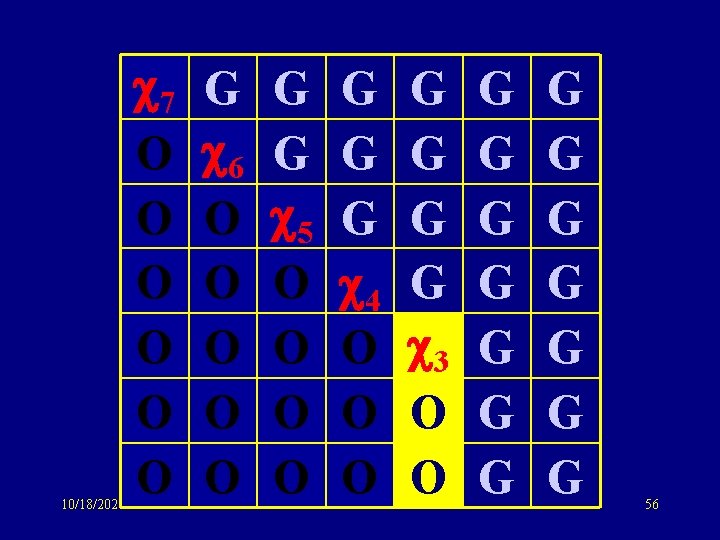
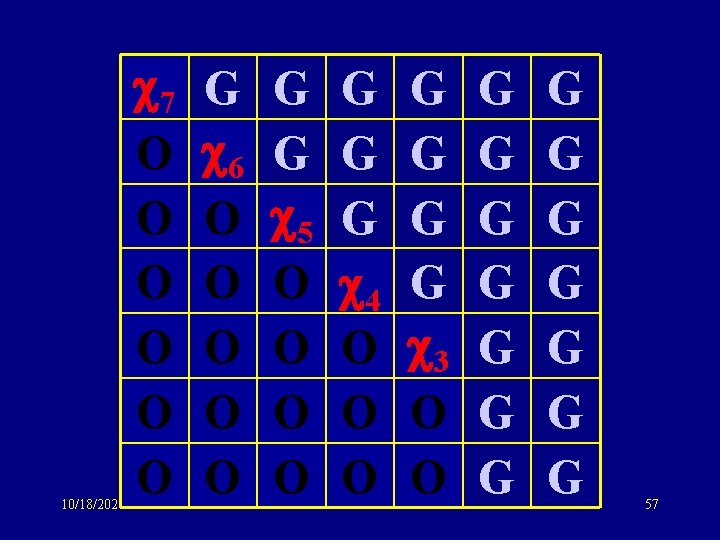
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G G 56

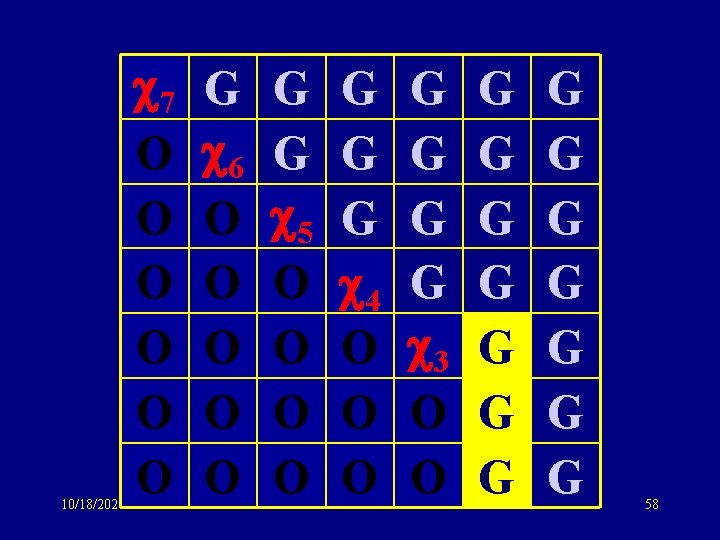
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G G 57

10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G G 58

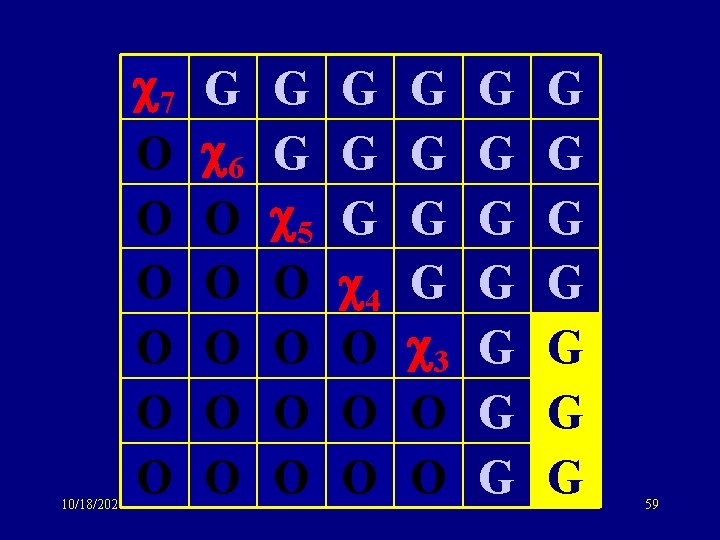
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G G 59

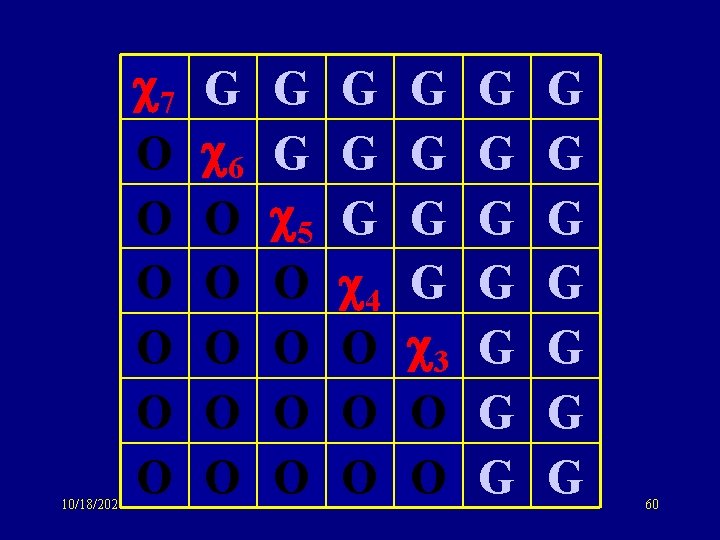
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G G 60

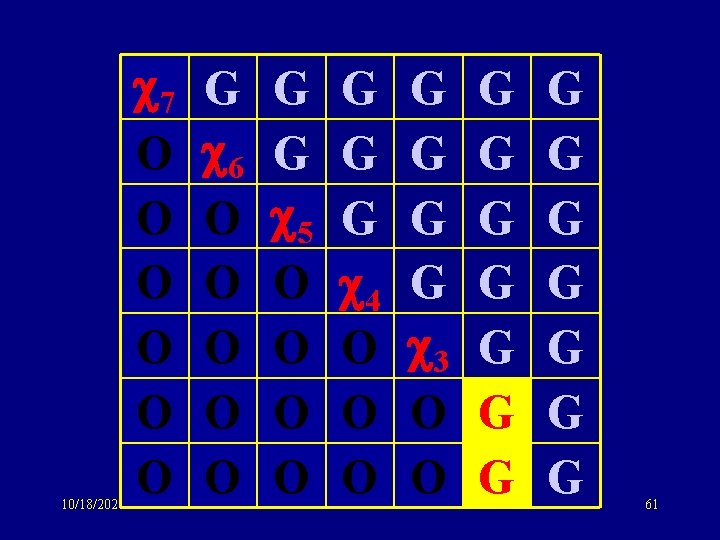
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G G 61

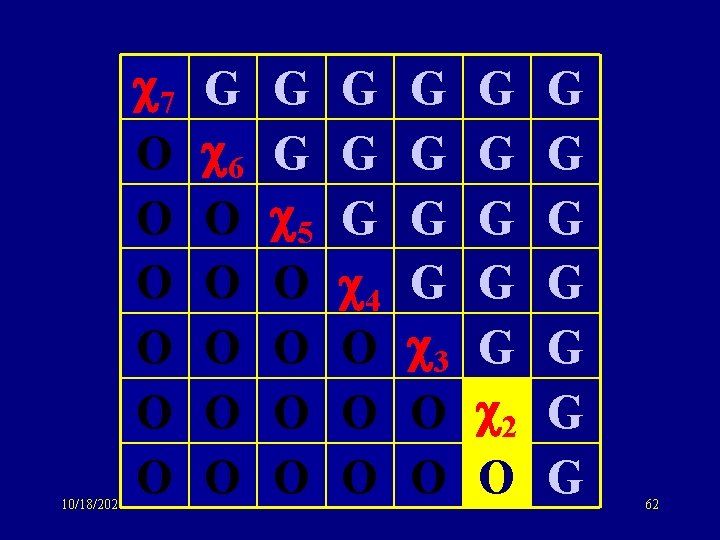
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G G 62

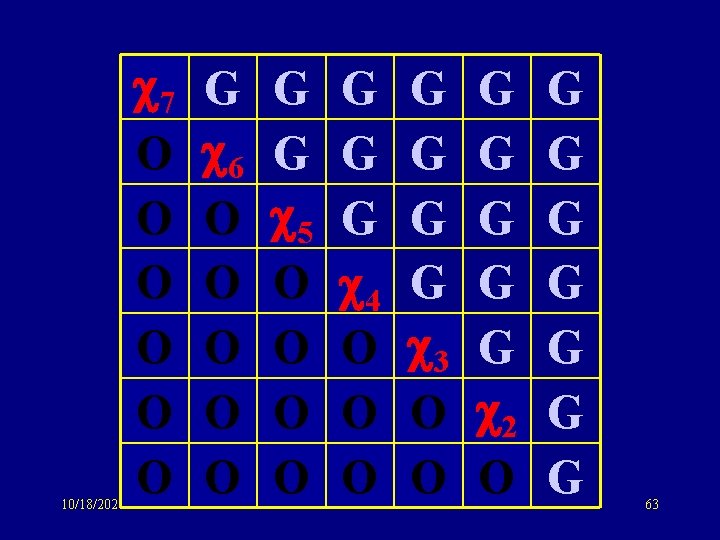
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G G 63

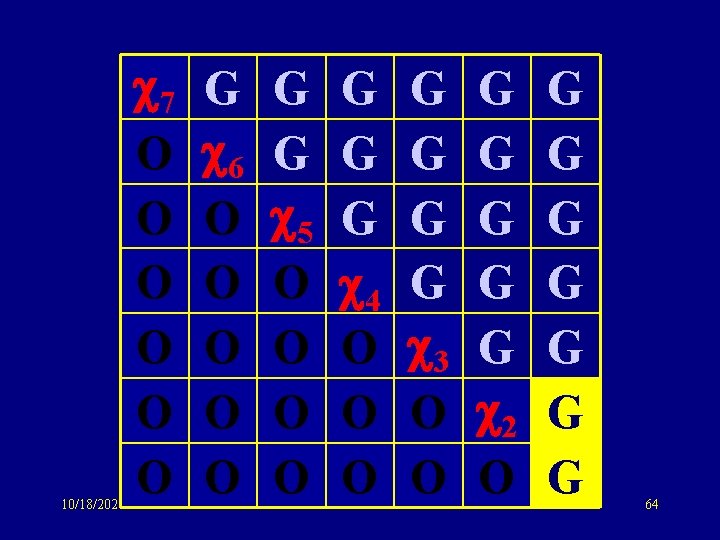
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G G 64

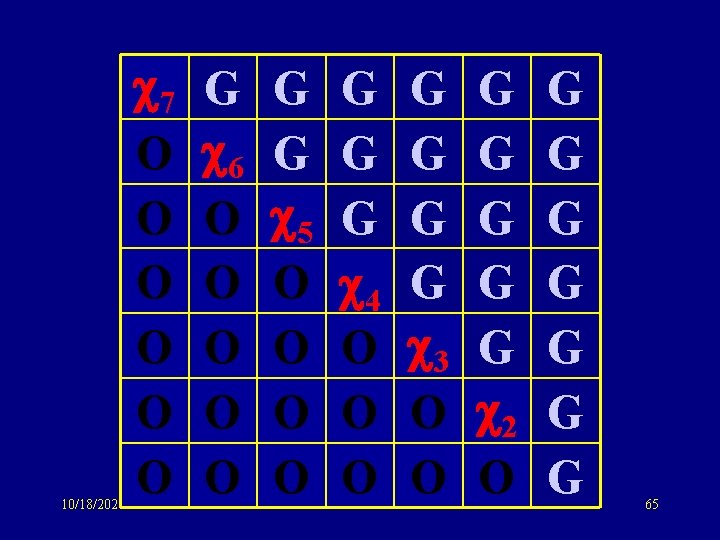
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G G 65

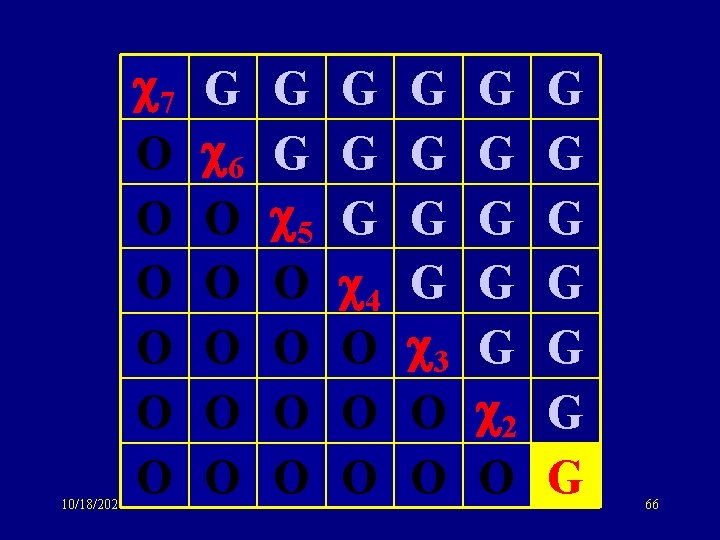
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G G 66

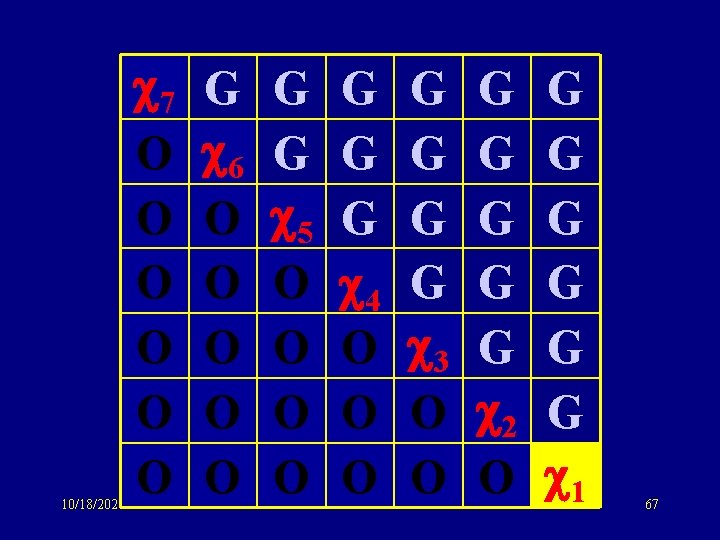
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G 1 67

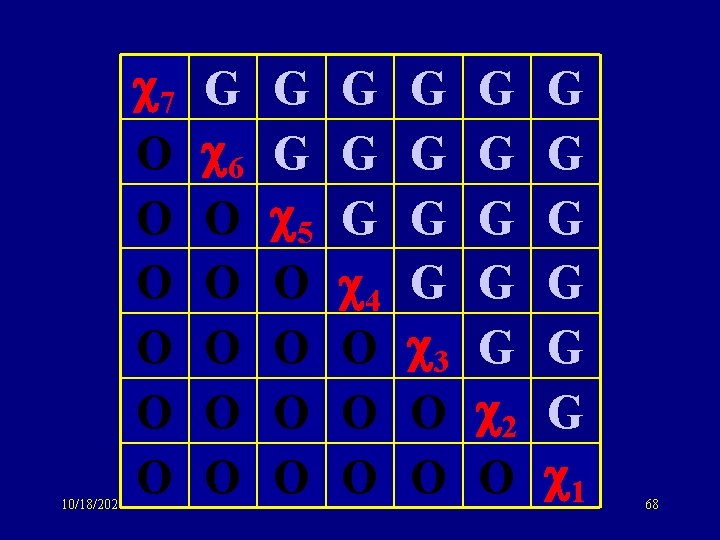
10/18/2021 7 O O O G 6 O O O G G 5 O O G G G 4 O O O G G 3 O O G G G 2 O G G G 1 68

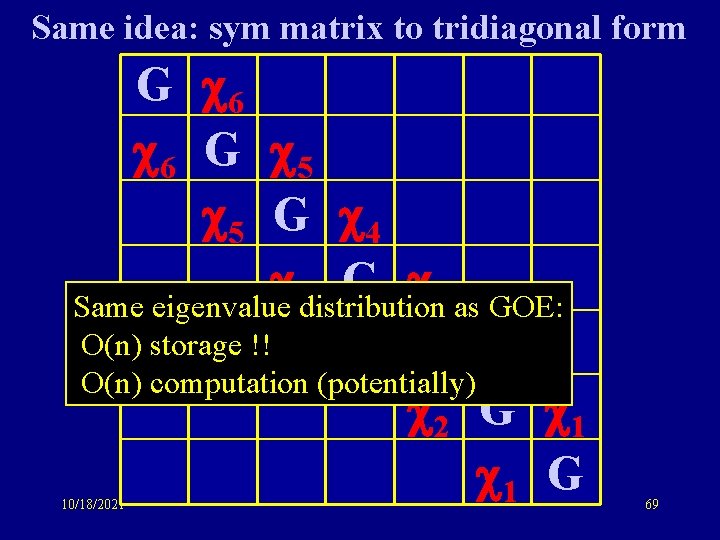
Same idea: sym matrix to tridiagonal form G 6 6 G 5 5 G 4 Same eigenvalue distribution 3 as GOE: O(n) storage !! 3 G 2 O(n) computation (potentially) 2 G 1 1 G 10/18/2021 69

Same idea: General beta G 6 beta: 1: reals 2: complexes 4: quaternions 6 G 5 5 GBidiagonal 4 Version corresponds of Statistics G matrices 4 To Wishart 3 3 G 2 2 G G 10/18/2021 70

v (A) Numerical Analysis: Condition Numbers = “condition number of A” v If A=U V’ is the svd, then (A) = max/ min. v Alternatively, (A) = max (A’A)/ min (A’A) v One number that measures digits lost in finite precision and general matrix “badness” v Small=good v Large=bad v The condition of a random matrix? ? ? 10/18/2021 71

Von Neumann & co. v Solve Ax=b via x= (A’A) -1 A’ b M A-1 Matrix Residual: ||AM-I||2 v ||AM-I||2< 200 2 n v v How should we estimate ? v Assume, as a model, that the elements of A are independent standard normals! 10/18/2021 72

Von Neumann & co. estimates (1947 -1951) v “For a ‘random matrix’ of order n the expectation value has been shown to be about X n” Goldstine, von Neumann v “… we choose two different values of , namely n and 10 n” P( <n) 0. 02 Bargmann, Montgomery, v. N P( < 10 n) 0. 44 v “With a probability ~1 … < 10 n” P( <10 n) 0. 80 10/18/2021 Goldstine, von Neumann 73

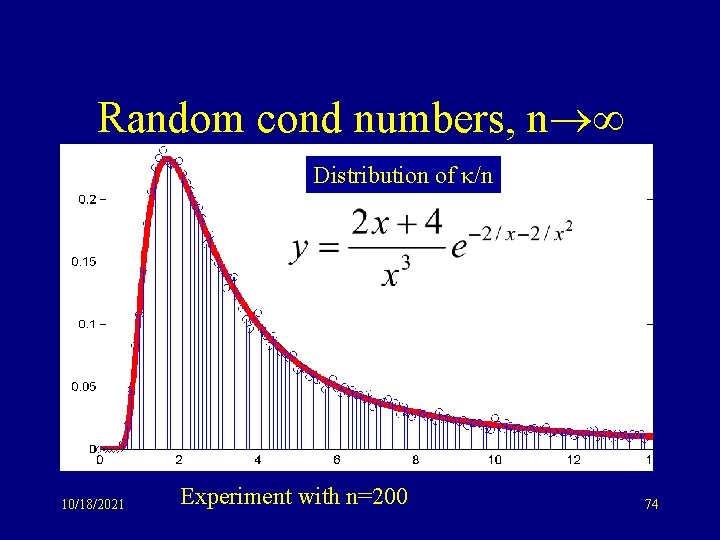
Random cond numbers, n Distribution of /n 10/18/2021 Experiment with n=200 74

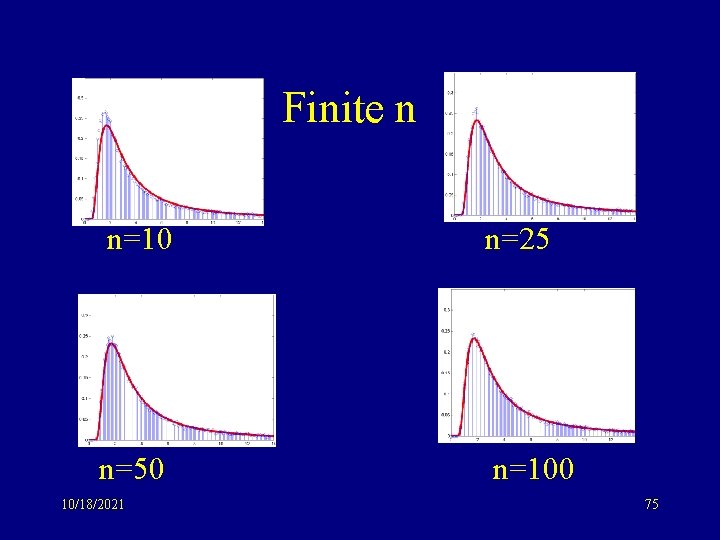
Finite n n=10 n=25 n=50 n=100 10/18/2021 75

Small World Networks: & 6 degrees of separation Edelman, Eriksson, Strang v Eigenvalues of A=T+PTP’, P=randperm(n) Incidence matrix of graph with two superimposed cycles. v 76

Small World Networks: & 6 degrees of separation Edelman, Eriksson, Strang v Eigenvalues of A=T+PTP’, P=randperm(n) Incidence matrix of graph with two superimposed cycles. v Wigner style derivation counts number of paths on a tree starting and ending at the same point (tree = no accidents!) (Mc. Kay) v We first discovered the formula using the superseeker 77 v Catalan number answer d 2 n-1 - d 2 j-1(d-1)n-j+1 Cn-j v

The Riemann Zeta Function On the real line with x>1, for example May be analytically extended to the complex plane, with singularity only at x=1. 10/18/2021 78

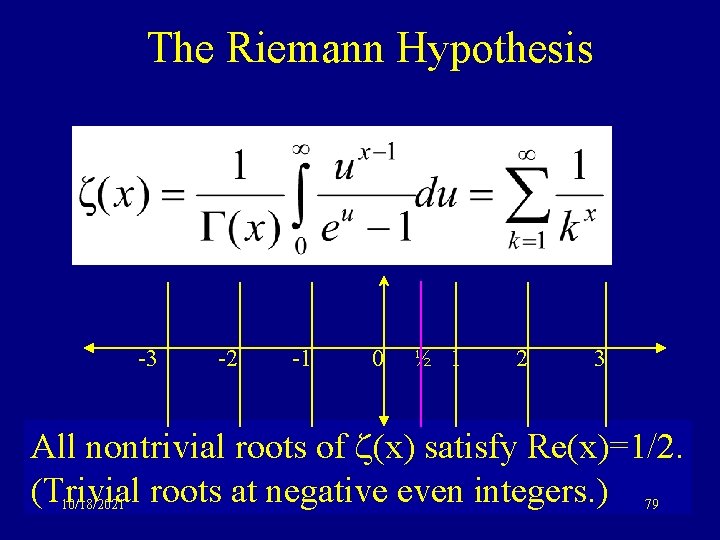
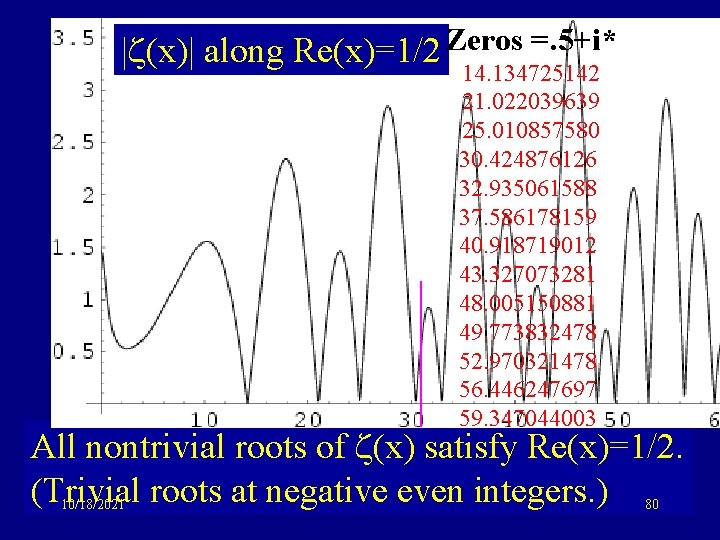
The Riemann Hypothesis -3 -2 -1 0 ½ 1 2 3 All nontrivial roots of (x) satisfy Re(x)=1/2. (Trivial roots at negative even integers. ) 10/18/2021 79

| (x)| along Re(x)=1/2 Zeros =. 5+i* 14. 134725142 21. 022039639 25. 010857580 30. 424876126 32. 935061588 37. 586178159 40. 918719012 43. 327073281 48. 005150881 49. 773832478 ½ 152. 970321478 2 3 56. 446247697 59. 347044003 The Riemann Hypothesis -3 -2 -1 0 All nontrivial roots of (x) satisfy Re(x)=1/2. (Trivial roots at negative even integers. ) 10/18/2021 80

Computation of Zeros v Odlyzko’s fantastic computation of 10^k+1 through 10^k+10, 000 for k=12, 21, 22. See http: //www. research. att. com/~amo/zeta_tables/ Spacings behave like the eigenvalues of A=randn(n)+i*randn(n); S=(A+A’)/2; 10/18/2021 81

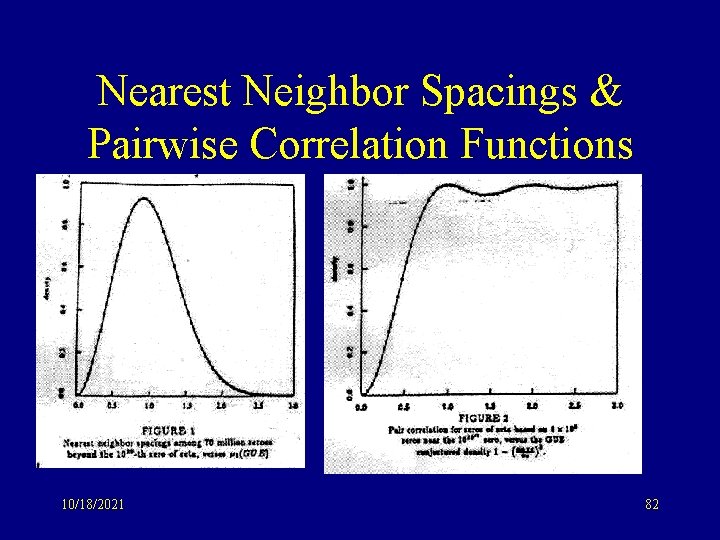
Nearest Neighbor Spacings & Pairwise Correlation Functions 10/18/2021 82

Painlevé Equations 10/18/2021 83

Spacings Take a large collection of consecutive zeros/eigenvalues. v Normalize so that average spacing = 1. v Spacing Function = Histogram of consecutive differences (the (k+1)st – the kth) v Pairwise Correlation Function = Histogram of all possible differences (the kth – the jth) v Conjecture: These functions are the same for random matrices and Riemann zeta v 10/18/2021 84

Some fun tidbits The circular law v The semi-circular law v Infinite vs finite v How many are real? v Stochastic Numerical Algorithms v Condition Numbers v Small networks v Riemann Zeta Function v Matrix Jacobians v 10/18/2021 85

Matrix Factorization Jacobians General uiin-i riim-i A=LU A=QR A=U VT ( i 2 - j 2) A=QS (polar) ( i+ j) A=X X-1 ( i- j)2 Sym S=Q QT S=LLT S=LDLT Orthogonal ( i- j) 2 n liin+1 -i Q=U C S VT sin( + )sin ( - ) i j S -C din-i [ ] Tridiagonal T=Q QT (ti+1, i)/ qi 10/18/2021 86

Why cool? v Why is numerical linear algebra cool? Mixture of theory and applications v Touches many topics v Easy to jump in to, but can spend a lifetime studying & researching v v Tons of activity in many areas Mathematics: Combinatorics, Harmonic Analysis, Integral Equations, Probability, Number Theory v Applied Math: Chaotic Systems, Statistical Mechanics, Communications Theory, Radar Tracking, Nuclear Physics v Applications v BIG HUGE SUBJECT!! v 10/18/2021 87