Applied Geometrical Matrix Computations Alan Edelman Dept of

Applied Geometrical Matrix Computations Alan Edelman Dept of Mathematics: MIT Laboratory for Computer Science Householder Symposium XV June 21, 2002

Outline • • • Geometrical Matrix Computations Illustration with 2 x 2 matrices: Excursions into eigenland (or why tangency and curvature matter!!) Where do matrix factorizations come from? Application to Color Science Matrix Animations

Geometrical Matrix Computations Working definition: • Concerns geometry of matrix space (n 2 dimensions rather than n) • Involves numerical computation (probably MATLAB) • Relates to an NLA problem Some Other GMC People Absil, Demmel, Elmroth, Huhtanen, Kagstrom, Kahan, Lippert, Mahony, Malyshev, Sepulchre, Tisseur, Trefethen, Van Dooren

Vector Space Diagrams • Points are vectors (not matrices!) • Geometric relationships for vectors, subspaces, and linear transformations

Outline • • • Geometrical Matrix Computations Illustration with 2 x 2 matrices: Excursions into eigenland (or why tangency and curvature matter!!) Where do matrix factorizations come from? Application to Color Science Matrix Animations

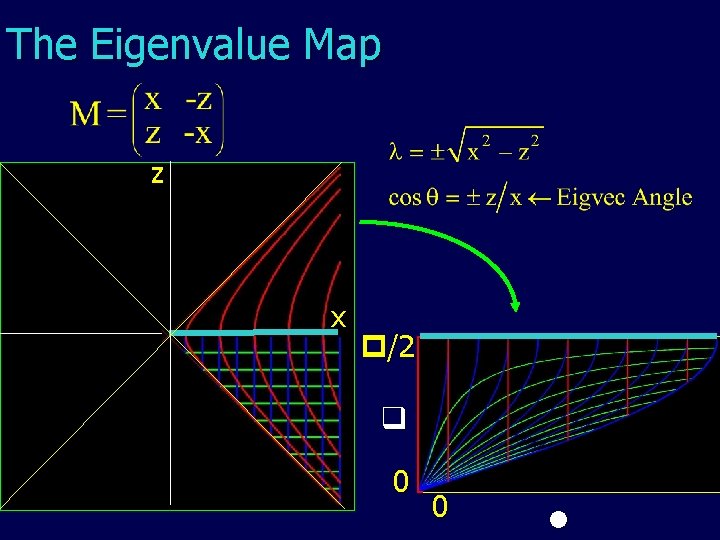
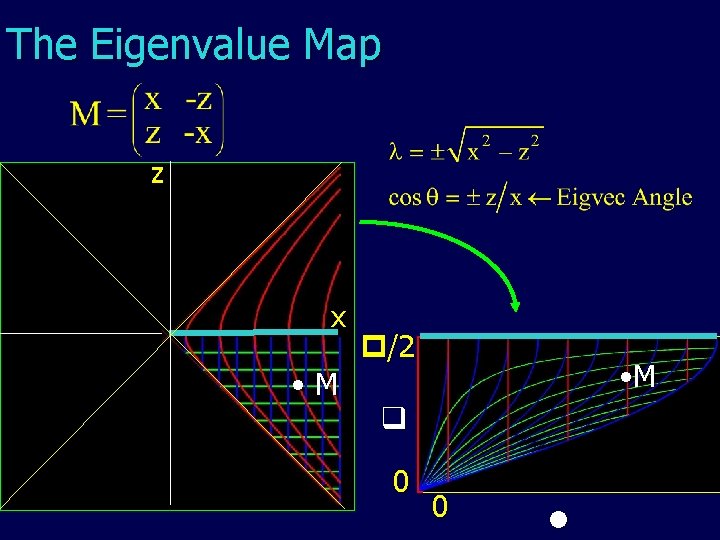
Eigenland (in 2 d) Isoeig surfaces are hyperbolas z x

The Eigenvalue Map zz xx / 2 Zero Matrix 0 0

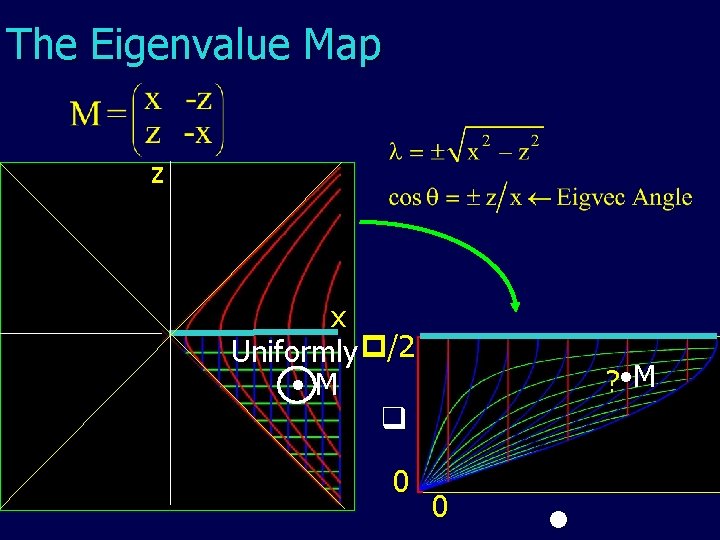
The Eigenvalue Map zz xx • M / 2 Zero Matrix 0 0 • M

The Eigenvalue Map zz xx Uniformly /2 • M Zero Matrix 0 0 ? • M

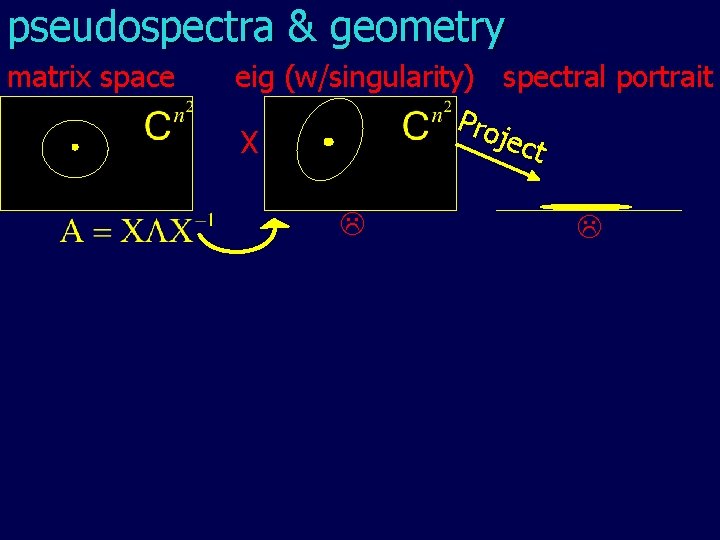
Pseudospectra (Trefethen) z z “z is an eigenvalue of a matrix near A” Pseudoportraits = pictures of contours of z Pseudoportraits 1 1 0 A= -1 0 1 -1 1 1 1 0 0 -1 1 1 0 0 0 -1 1 Random Points

pseudospectra & geometry matrix space eig (w/singularity) spectral portrait Pro ject X L L

Outline • • • Geometrical Matrix Computations Illustration with 2 x 2 matrices: Excursions into eigenland (or why tangency and curvature matter!!) Where do matrix factorizations come from? Application to Color Science Matrix Animations

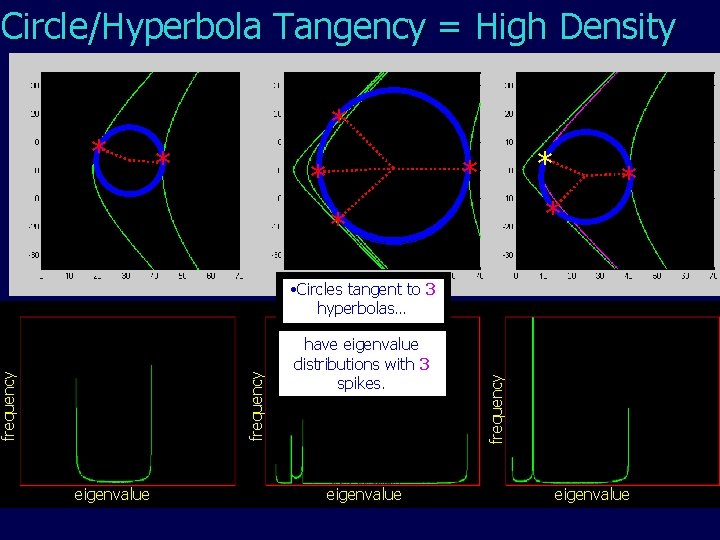
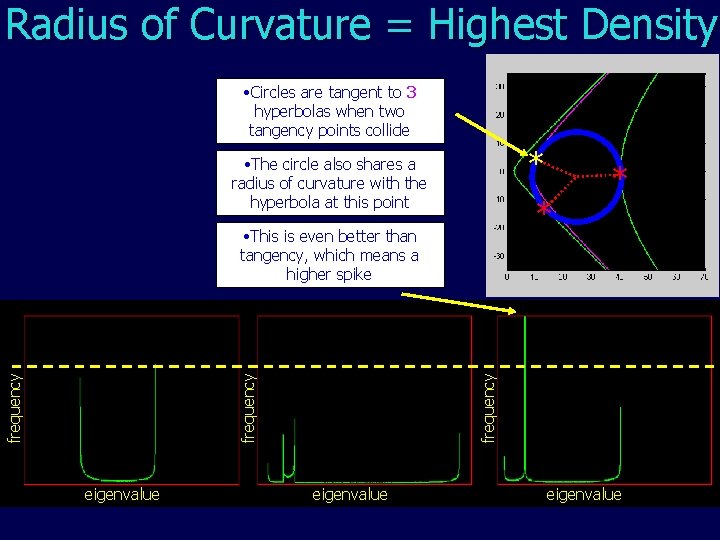
Circle/Hyperbola Tangency = High Density * * * * * eigenvalue have eigenvalue 2 distributions with 3 4 spikes. eigenvalue frequency • Circles tangent to 2 4 3 hyperbolas… eigenvalue

Radius of Curvature = Highest Density • Circles are tangent to 3 hyperbolas when two tangency points collide * • The circle also shares a radius of curvature with the hyperbola at this point * frequency • This is even better than tangency, which means a higher spike eigenvalue * eigenvalue

Outline • • • Geometrical Matrix Computations Illustration with 2 x 2 matrices: Excursions into eigenland (or why tangency and curvature matter!!) Where do matrix factorizations come from? Application to Color Science Matrix Animations

Where do Matrix Factorizations Come From? Classical Answer: A=U V’ Representation Theory of Semisimple Groups

Semisimple group recipe • Nicely links factorizations • Three Examples Nonsingulars Unitary SVD Uei V’ SPD Eigen Uei U’ One more example Hyperbolic Svd as in last talk Group = SO(p, q) ( XJ=JX) Orthogonal CS decomp Essentially Sym Orth

Matrix Factorizations Where can we look for new factorizations? • The Mathematics Literature – Lie Algebra: Cartan, Iwasawa, Bruhat – Representation Theory: Quivers • Nearness Problems • Applications – Engineering: A factorization is useful if someone can use it – Mathematics: The useful factorizations are characterized by an abstract criterion

Ideas to Generalize 1: Cartan Decomposition E = (antisymmetric) + (symmetric) expm M= Non-singular expm Q Orthogonal expm * S Pos Definite [polar]

Ideas to Generalize 1: Cartan Decomposition E = (antisymmetric) + (symmetric) expm M= Non-singular expm Q Orthogonal expm * S Pos Definite 2: KAK Decomposition Positive Diagonals = Maximal Group M=U V’ Conjugates give S=Q Q’ [polar]

Ideas to Generalize 1: Cartan Decomposition E = (antisymmetric) + (symmetric) expm M= Non-singular expm Q Orthogonal expm * S [polar] Pos Definite 2: KAK Decomposition Positive Diagonals = Maximal Group M=U V’ Conjugates give S=Q Q’ 3: Iwasawa, Bruhat Above not unique at I. Gives M= LU, other permutations, totally positive, etc

Ideas to Generalize 1: Cartan Decomposition E = (antisymmetric) + (symmetric) expm M= Non-singular expm Q Orthogonal expm * S [polar] Pos Definite 2: KAK Decomposition Positive Diagonals = Maximal Group M=U V’ Conjugates give S=Q Q’ 3: Iwasawa, Bruhat Above not unique at I. Gives M= LU, other permutations, totally positive, etc 4: Eigenvalue, Jordan Schur

Step 1: Cartan Decomposition • Group: non-singular matrices • Involution: ( (M))=M (M 1 M 2)= (M 1) (M 2) (M)=M-T • Fixed Points (M)=M are a group K K = orthogonal matrices • Near I M = (antisymmetric) + (symmetric) • Cartan: expm M = QS (S>0) (polar)

Step 1: Cartan Decomposition (U/O) • Group: unitary matrices • Near I M = (antisymmetric) + (i*symmetric) • Cartan: M= (real orth)(unitary symmetric)

Step 2: KAK Decomposition P = sym pos def • A = biggest group inside P (abelian) e. g. diagonal > 0, or conjugates U U’ (fix U) • KAK M=U V’ • P = union of conjugates S=Q Q’

Step 2: KAK Decomposition (U/Q) P = unitary symmetric • A = biggest group inside P (abelian) e. g. diagonals (ei ) or conjugates • KAK M=Uei V’ (U, V real orthogonal) • P = union of conjugates S=Qei Q’ (Q real orthogonal)

Step 2: KAK Decomposition (On/Op X Oq ) C P = matrices orthogonally similar to ( -S • A = biggest group inside P (abelian) C S e. g. =( -S C ) or conjugates • KAK The CS Decomposition S C )

Missing • The constructible decompositions Tridiagonalization, Bidiagonalization • The NNMF (Lee, Seung 1999) • V WH Input: Vij>0 Output: Wij>0 Hij>0 (low rank) Algorithm: H H. * (W’V). /(W’WH) W W. * (VH’). /(WHH’) Original Application: Eigenfaces Another Example: Color Science

Outline • • • Geometrical Matrix Computations Illustration with 2 x 2 matrices: Excursions into eigenland (or why tangency and curvature matter!!) Where do matrix factorizations come from? Application to Color Science Matrix Animations

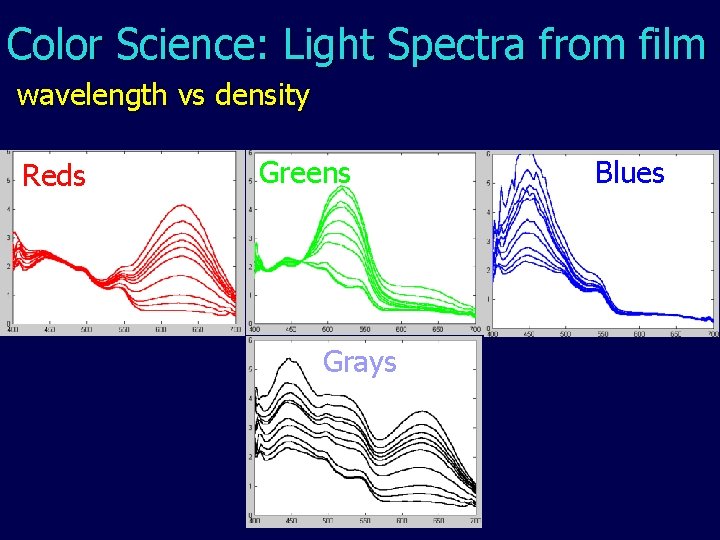
Color Science: Light Spectra from film wavelength vs density Reds Greens Grays Blues

Film Recording and measurements • Solid colors sent to film recorder, e. g. reds • Negative is produced: film appears as cyans • Negative sent through projector to spectrometer • Energy data at each wavelength Reds • Log ratio with no film (only bulb) film density = log(no film / with film)

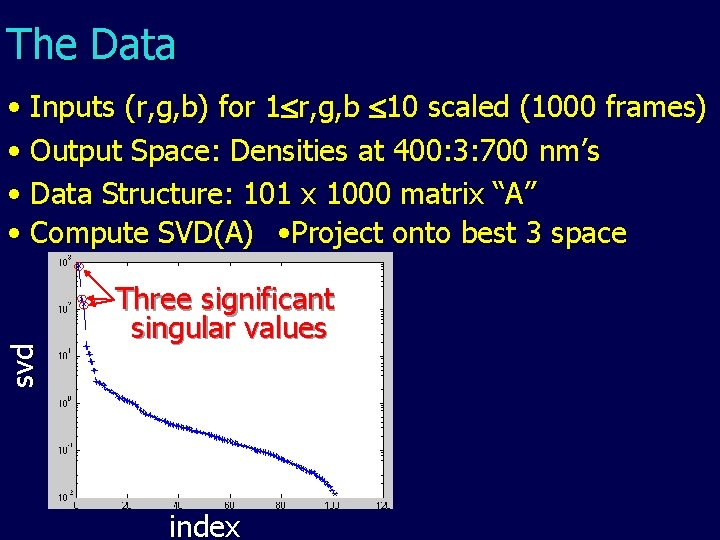
The Data svd • Inputs (r, g, b) for 1 r, g, b 10 scaled (1000 frames) • Output Space: Densities at 400: 3: 700 nm’s • Data Structure: 101 x 1000 matrix “A” • Compute SVD(A) • Project onto best 3 space Three significant singular values index

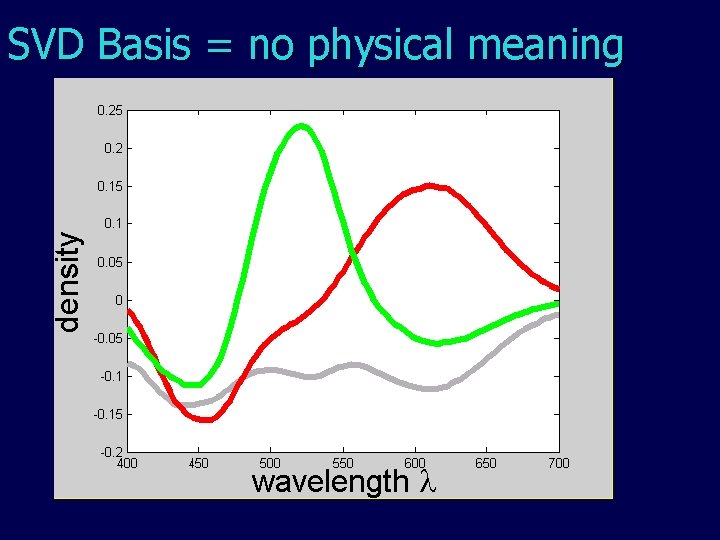
SVD Basis = no physical meaning

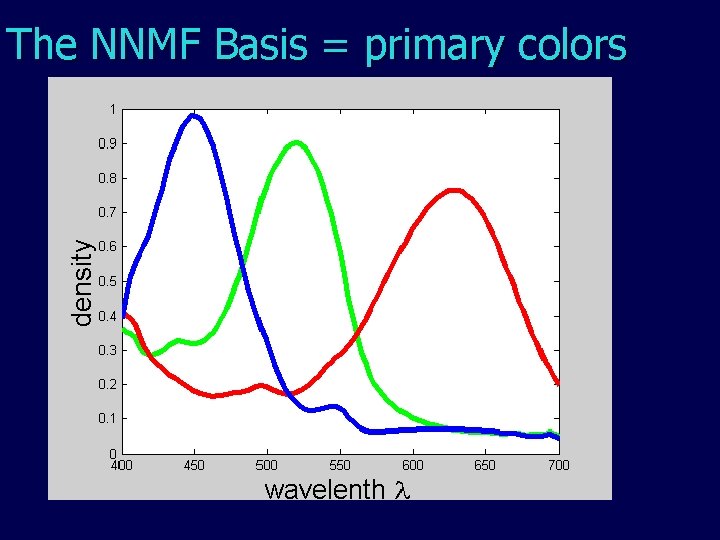
The NNMF Basis = primary colors

Outline • • • Geometrical Matrix Computations Illustration with 2 x 2 matrices: Excursions into eigenland (or why tangency and curvature matter!!) Where do matrix factorizations come from? Application to Color Science Matrix Animations

Singular 2 x 2 Matrices (by svd) _ ( cos A= -sin cos sin -sin ) Torus! Torus Cone? All isoeig surfaces are translates of the =0 surface! hyperpolas and hyperboloids are cross sections!

Bohemian Dome

Linear Algebra with movies Horizontal A=Q QT Vertical A=Q Q Villarceau A=QR Hopf Fibration

Challenges Incorporate 3 d graphics tools directly into Matrix computations. Include geometry of matrix space. How should this look? Generalize everything and incorporate into software