Estimation of Eigenvalues Largest eigenvalue Power Method Smallest

Estimation of Eigenvalues ü Largest eigenvalue: Power Method ü Smallest eigenvalue: Inverse Power Method ü All Eigenvalues: ü Inverse power method with shift ü Faddeev-Leverrier method ü QR Decomposition

The Power Method Works if: There is a unique eigenvalue of maximum magnitude! There are n independent eigenvectors corresponding to n eigenvalues

The Power Method Initialize an arbitrary non-zero vector (z(0)) of length n (same as that of the size of the square matrix) Iteration Scheme: The vector (z(k)) converges to the eigenvector corresponding to the eigenvalue of the maximum magnitude! Why? How?

Proof of Convergence: Power Method Denote xi as the eigenvector corresponding to the eigenvalue λi αi’s are the constants Since,

Proof of Convergence: Power Method Denote xi as the eigenvector corresponding to the eigenvalue λi αi’s are the constants Since,

Proof of Convergence: Power Method Denote xi as the eigenvector corresponding to the eigenvalue λi αi’s are the constants Since,

Proof of Convergence: Power Method Denote xi as the eigenvector corresponding to the eigenvalue λi αi’s are the constants Since, For Large k:

Power Method Algorithm Initialize an arbitrary non-zero vector z(0) Iterate: Stop when: Compute the largest eigenvalue as: since

The Inverse Power Method ü Apply power method on matrix A-1 to obtain the largest eigenvalue. Inverse of this eigenvalue is the smallest eigenvalue of A ü Proposition: Inverse of the largest eigenvalue of A-1 is the smallest eigenvalue of A ü For any eigenvalue λi and corresponding eigenvector xi of matrix A: Axi = λixi ü Since λi is a scalar, (1/λi)xi = A-1 xi ü If λi is an eigenvalue of matrix A, (1/λi) is an eigenvalue of A-1 with the same corresponding eigenvector xi

Inverse Power Method with Shift ü Apply power method on matrix (A – αI)-1 to obtain the eigenvalue that is closest to constant α. ü For any eigenvalue λi and corresponding eigenvector xi of matrix A: Axi = λixi ü For a scalar constant α, Axi - αxi = λixi - αxi ü (A – αI)xi = (λi - α)xi, (λi - α) is an eigenvalue of the matrix (A – αI). ü Smallest eigenvalue of matrix (A – αI) corresponds to that eigenvalue of matrix A that is closest in magnitude to the scalar constant α ü This gives an algorithm to estimate an eigenvalue of a matrix that is closest to a given constant!

11

12

13

Faddeev Leverrier Method

15

Similarity Transformation

Computation of Eigenvalues ü Recall: What is an orthogonal matrix? ü Each column vector is orthonormal to each other ü QTQ = I or QT = Q-1 ü A n × n matrix is non-defective if it has n independent eigenvectors (rank n, non-zero determinant, inverse exists, etc. ) ü For every non-defective real matrix A with real eigenvalues, there is an orthogonal matrix Q and an upper -triangular matrix U such that A = QUQT ü If A is complex, Q is unitary such that A = QUQH ü Therefore, A and U are similar matrices, A = QUQT ü The upper triangular matrix U contains the eigenvalues of A on its diagonal.

Computation of Eigenvalues ü All non-defective matrices are similar to upper triangular matrices ü A = QUQT or U = QTAQ, U contains the eigenvalues of A on its diagonal. ü Therefore, a non-defective matrix A can be transformed to an upper-triangular matrix U through similarity transformation and the diagonal elements of U will be the eigenvalues. ü This transformation cannot be achieved in one step. It is achieved through a sequence of similarity transformation using QR-decomposition!

Computation of Eigenvalues

QR-Decomposition a(1) a(2) a(j) q(1) q(2) a(n) q(j) q(n) r(1) r(2) r(j) r(n)

QR-Decomposition: proof by induction

QR-Decomposition: proof by induction

23

QR-Decomposition: proof by induction

25

26

27

QR-Decomposition: Algorithm

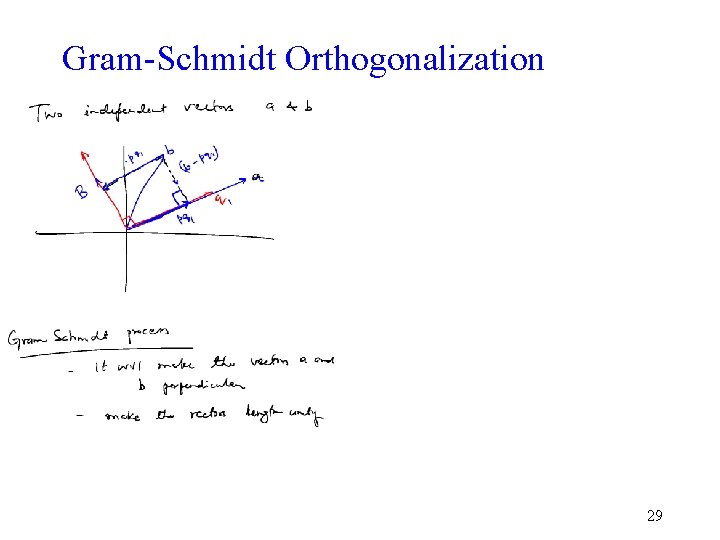
Gram-Schmidt Orthogonalization 29

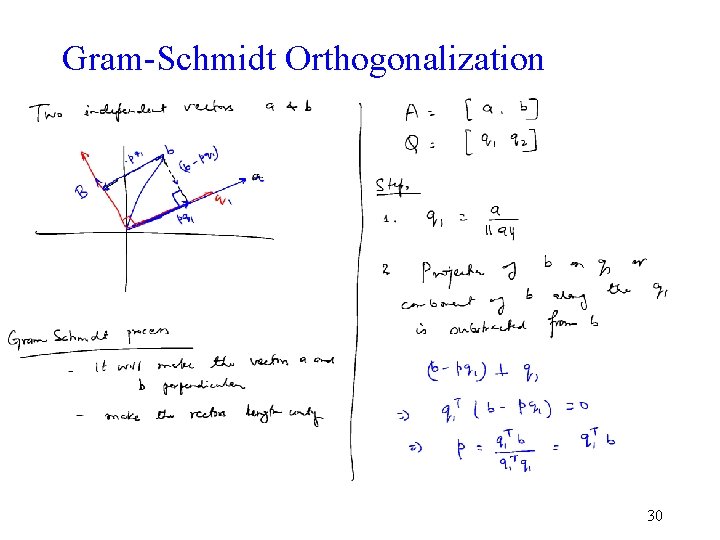
Gram-Schmidt Orthogonalization 30

Gram-Schmidt Orthogonalization 31

Gram-Schmidt Orthogonalization 32

Gram-Schmidt Orthogonalization 33