Vpeto drevo Vsak povezan graf ima vpeto drevo

![Naloge • • • Določi drevo za naslednje kode: [1, 1, 1, 1] [1, Naloge • • • Določi drevo za naslednje kode: [1, 1, 1, 1] [1,](https://slidetodoc.com/presentation_image_h/fa0ab29b3214200afb1f4a89da1e5e4e/image-6.jpg)












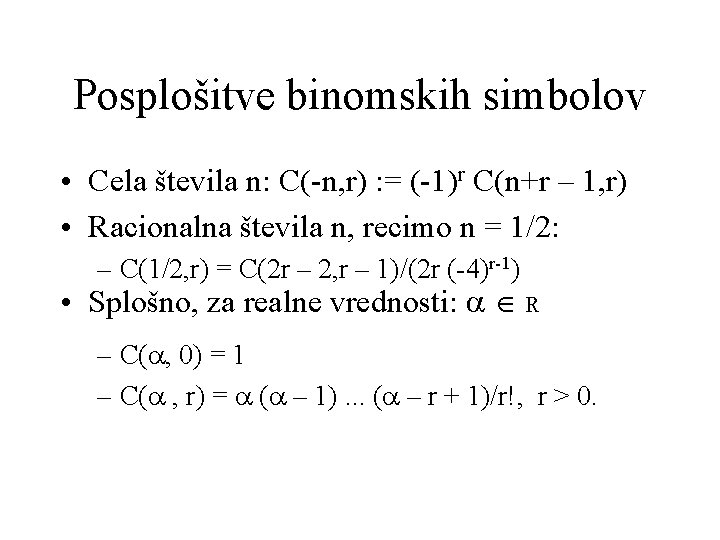












- Slides: 42

Vpeto drevo • Vsak povezan graf ima vpeto drevo. • Za končne grafe lahko to pokažemo hitro. [Dokler ne dobimo drevesa, odstranjujemo primerne povezave]. • Za neskončne grafe pa to ni izrek ampak je dejstvo, ekvivalentno aksiomu izbire.

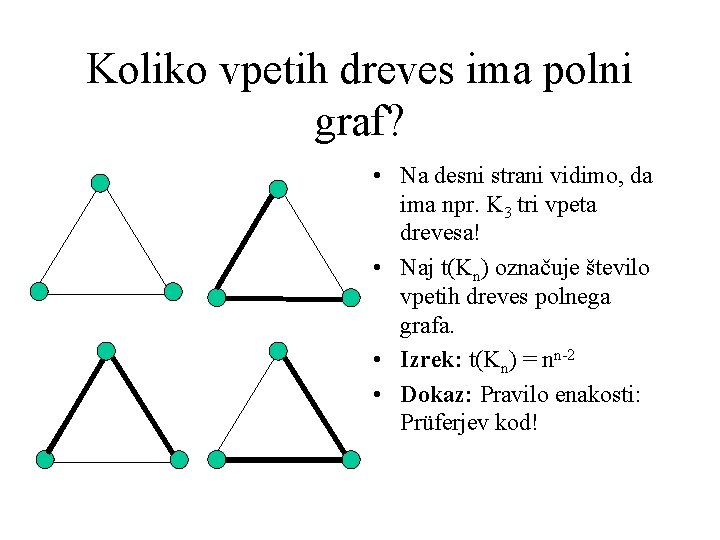
Koliko vpetih dreves ima polni graf? • Na desni strani vidimo, da ima npr. K 3 tri vpeta drevesa! • Naj t(Kn) označuje število vpetih dreves polnega grafa. • Izrek: t(Kn) = nn-2 • Dokaz: Pravilo enakosti: Prüferjev kod!

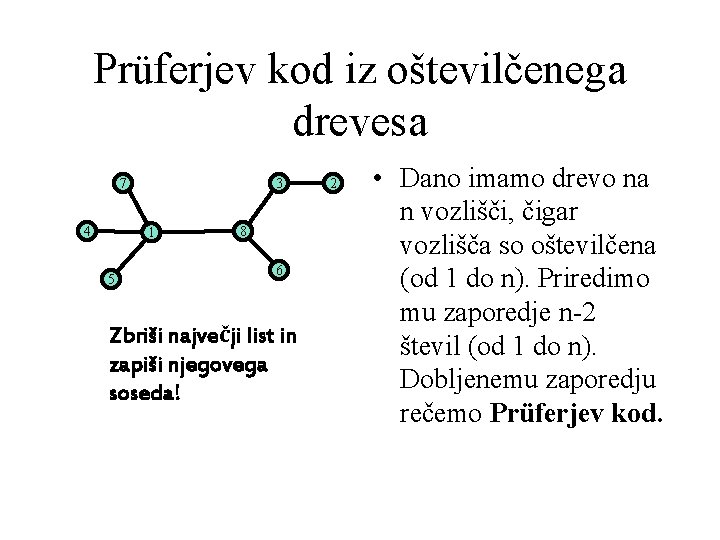
Prüferjev kod iz oštevilčenega drevesa 7 4 3 1 5 8 6 Zbriši največji list in zapiši njegovega soseda! 2 • Dano imamo drevo na n vozlišči, čigar vozlišča so oštevilčena (od 1 do n). Priredimo mu zaporedje n-2 števil (od 1 do n). Dobljenemu zaporedju rečemo Prüferjev kod.

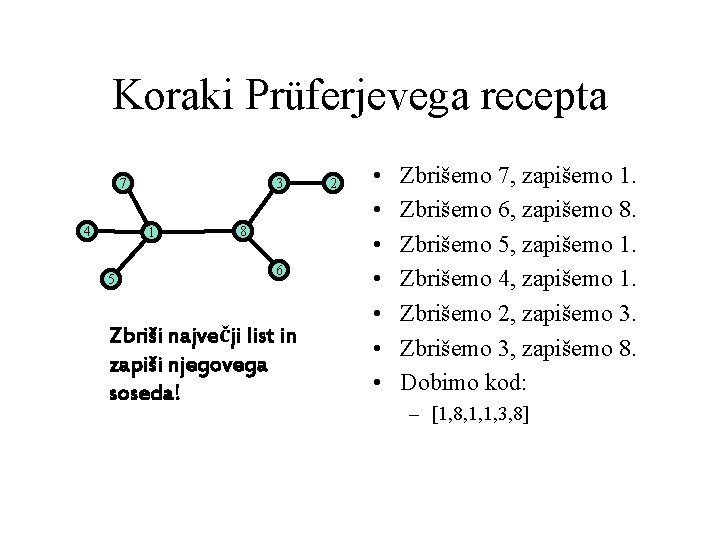
Koraki Prüferjevega recepta 7 4 3 1 5 8 6 Zbriši največji list in zapiši njegovega soseda! 2 • • Zbrišemo 7, zapišemo 1. Zbrišemo 6, zapišemo 8. Zbrišemo 5, zapišemo 1. Zbrišemo 4, zapišemo 1. Zbrišemo 2, zapišemo 3. Zbrišemo 3, zapišemo 8. Dobimo kod: – [1, 8, 1, 1, 3, 8]

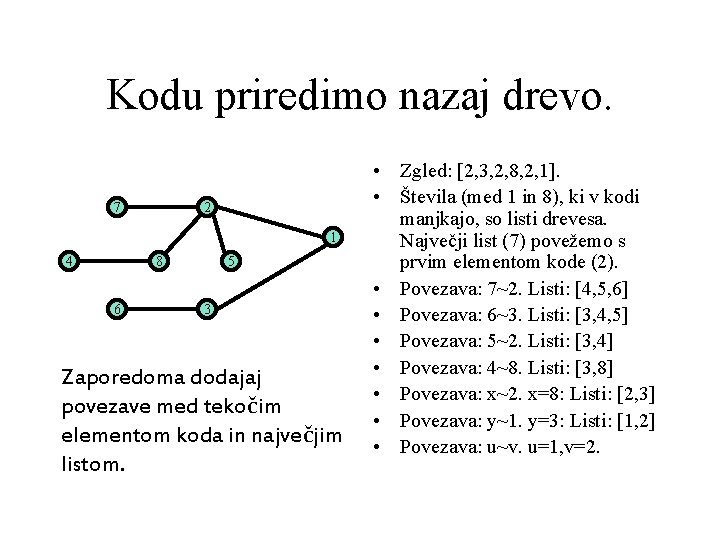
Kodu priredimo nazaj drevo. 7 2 1 4 8 6 5 3 Zaporedoma dodajaj povezave med tekočim elementom koda in največjim listom. • Zgled: [2, 3, 2, 8, 2, 1]. • Števila (med 1 in 8), ki v kodi manjkajo, so listi drevesa. Največji list (7) povežemo s prvim elementom kode (2). • Povezava: 7~2. Listi: [4, 5, 6] • Povezava: 6~3. Listi: [3, 4, 5] • Povezava: 5~2. Listi: [3, 4] • Povezava: 4~8. Listi: [3, 8] • Povezava: x~2. x=8: Listi: [2, 3] • Povezava: y~1. y=3: Listi: [1, 2] • Povezava: u~v. u=1, v=2.
![Naloge Določi drevo za naslednje kode 1 1 1 1 1 Naloge • • • Določi drevo za naslednje kode: [1, 1, 1, 1] [1,](https://slidetodoc.com/presentation_image_h/fa0ab29b3214200afb1f4a89da1e5e4e/image-6.jpg)
Naloge • • • Določi drevo za naslednje kode: [1, 1, 1, 1] [1, 2, 1, 2] [1, 2, 3, 3, 2, 1] [1, 2, 3, 4, 5, 4, 3, 2, 1] [6, 1, 6, 1]

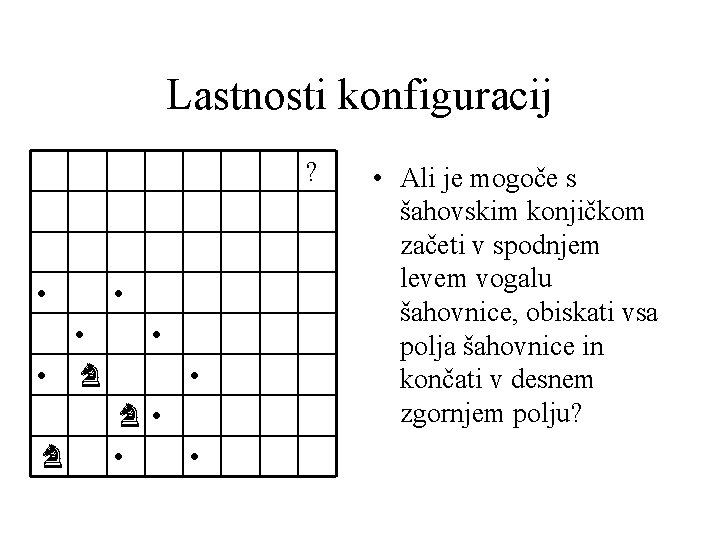
Lastnosti konfiguracij ? • • ♞ • • Ali je mogoče s šahovskim konjičkom začeti v spodnjem levem vogalu šahovnice, obiskati vsa polja šahovnice in končati v desnem zgornjem polju?

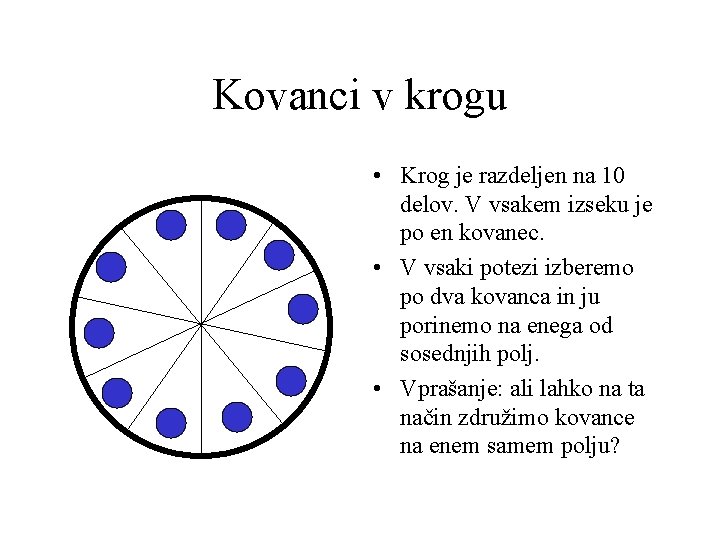
Kovanci v krogu • Krog je razdeljen na 10 delov. V vsakem izseku je po en kovanec. • V vsaki potezi izberemo po dva kovanca in ju porinemo na enega od sosednjih polj. • Vprašanje: ali lahko na ta način združimo kovance na enem samem polju?

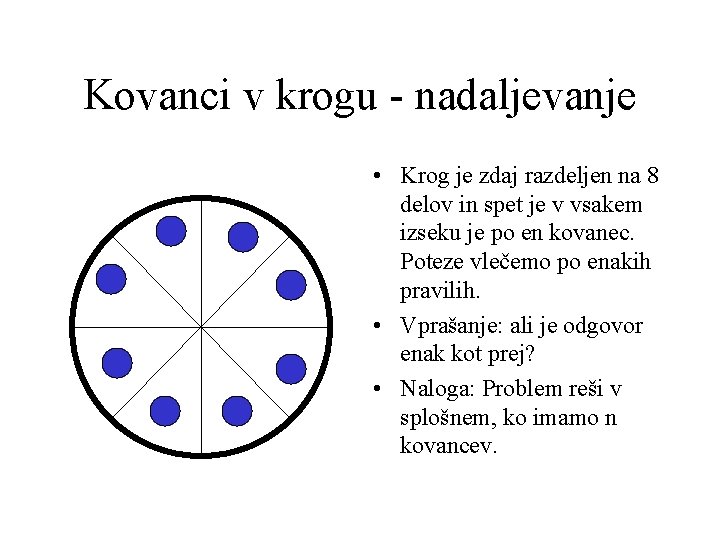
Kovanci v krogu - nadaljevanje • Krog je zdaj razdeljen na 8 delov in spet je v vsakem izseku je po en kovanec. Poteze vlečemo po enakih pravilih. • Vprašanje: ali je odgovor enak kot prej? • Naloga: Problem reši v splošnem, ko imamo n kovancev.

Klasične konfiguracije - Izbori

Klasične konfiguracije - Izbori • Izbori – Izbiramo r elementov iz množice A. Ločimo jih na štiri primere: urejen neurejen ponavljanje V¯(A, r) C¯ (A, r) Brez ponavljanja V(A, r) C(A, r)

Klasične konfiguracije nadaljevanje • Urejeni izbori: variacije. • Neurejeni izbori: kombinacije. ponavljanje urejen neurejen V¯(A, r) C¯ (A, r) Variacije s ponavljanjem Brez ponavljanja V(A, r) Variacije Kombinacije s ponavljanjem C(A, r) Kombinacije

Variacije reda r s ponavljanjem • Variacije reda r s ponavljanjem: V¯(A, r). • Zgled: A = {a, b, c}, r = 2. a a a b a c • V¯(3, 2) = 9 b a b b b c c a c b c c

Variacije reda r s ponavljanjem nadaljevanje • • • V¯(n, 0) = 1 V¯(n, r) = n V¯(n, r-1), r > 0. Prva vrstica je očitna. Druga vrstica uporablja pravilo produkta. Z matematično indukcijo po r lahko dokažemo: • V¯(n, r) = nr

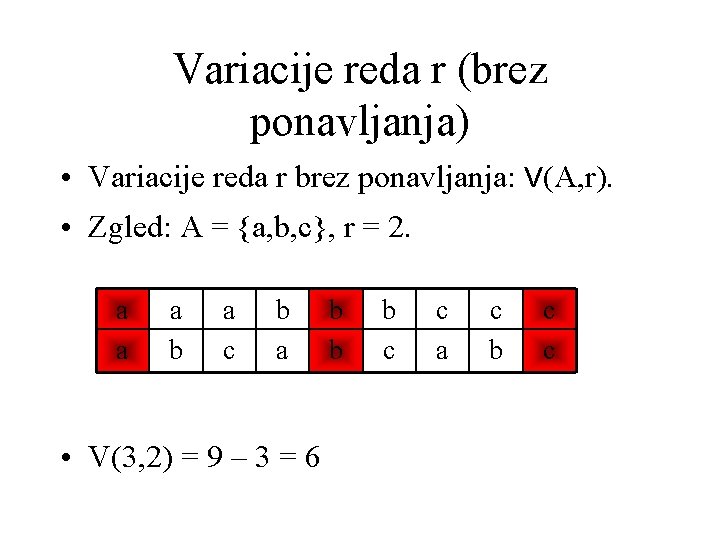
Variacije reda r (brez ponavljanja) • Variacije reda r brez ponavljanja: V(A, r). • Zgled: A = {a, b, c}, r = 2. a a a b a c b a • V(3, 2) = 9 – 3 = 6 b b b c c a c b c c

Variacije reda r - nadaljevanje • • • V(n, 0) = 1, n ≥ 0 V(0, r) = 0, r > 0 V(n, r) = n V(n-1, r-1), r > 0. Prvi dve vrstici sta očitni. Tretja vrstica uporablja posplošeno pravilo produkta. • Z matematično indukcijo lahko dokažemo: • V(n, r) = n(n-1). . . (n-r+1) : = n[r]

Permutacije • • V(n, r) = 0, za r > n. Zanimiv je mejni primer n = r: P(n) : = V(n, n) so permutacije. P(0) = 1. P(n) = n P(n-1). Velja: P(n) = n(n-1). . . 2. 1 = n!

Permutacije - nadaljevanje • Funkcija n! (n-faktorialno) zelo hitro raste: • Za ocene uporabljamo: n • Stirlingov približek: 0 • Naloga: napiši program – ki preveri kvaliteto približka – (primerja original in približek) n! 1 1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880

Matematična indukcija – še enkrat. • Z matematično indukcijo dokazujemo veljavnost neke trditve, recimo P(n), za vsa naravna števila n. Uporabljamo dva koraka. • Baza indukcije. Posebej moramo dokazati, da trditev velja za nek majhen n, recimo, za n = 1. – P(1). • Indukcijski korak. Na osnovi predpostavke, da velja P(n) dokažemo, da velja P(n+1): – P(n) P(n+1).

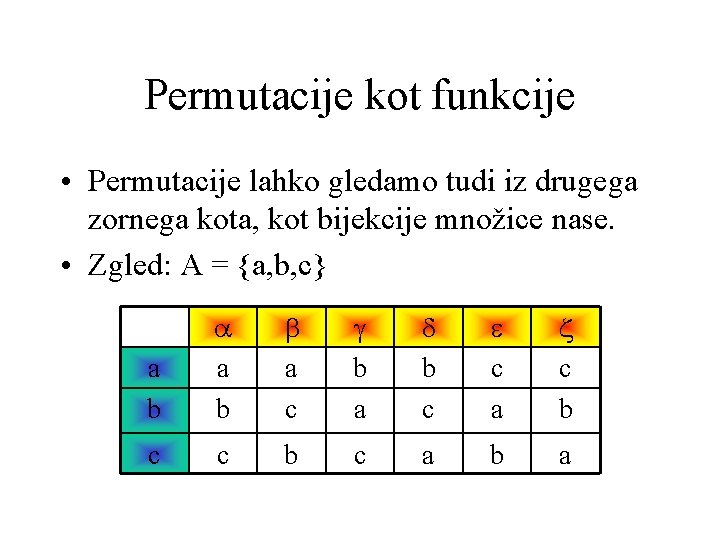
Permutacije kot funkcije • Permutacije lahko gledamo tudi iz drugega zornega kota, kot bijekcije množice nase. • Zgled: A = {a, b, c} a b a a b b a c g b a d b c e c a z c b c a b a

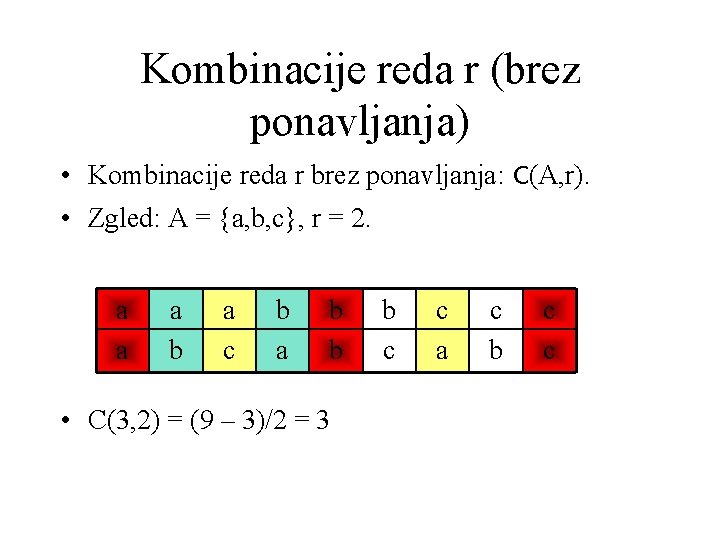
Kombinacije reda r (brez ponavljanja) • Kombinacije reda r brez ponavljanja: C(A, r). • Zgled: A = {a, b, c}, r = 2. a a a b a c b a b b • C(3, 2) = (9 – 3)/2 = 3 b c c a c b c c

Kombinacije reda r - nadaljevanje • • • C(n, r) = V(n, r)/P(r) = n!/(r!(n-r)!) C(n, 0) = 1 C(n, n) = 1 C(n, r) = C(n-1, r) + C(n-1, r-1). Prvo vrstico dobimo s posplošitvijo sklepa iz prejšnje strani. • Druga in tretja vrstica sta očitni. • Četrta vrstica uporablja pravilo vsote in “označeni element” v množici A.

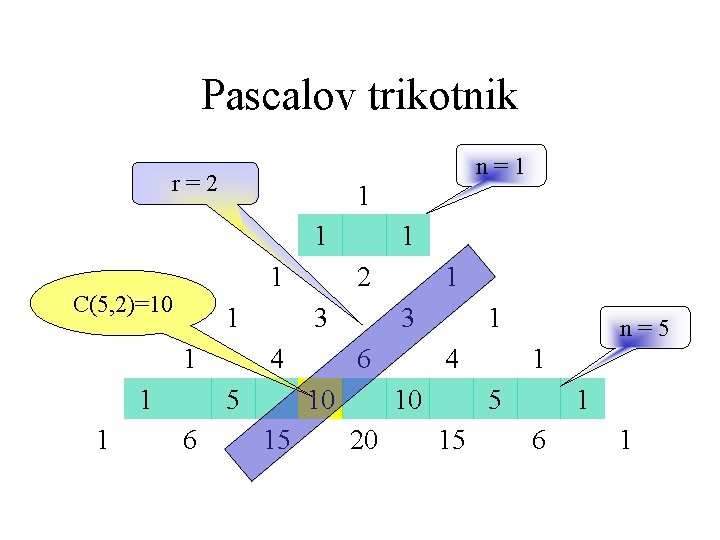
Pascalov trikotnik n=1 r=2 1 1 1 C(5, 2)=10 1 1 2 3 4 5 6 1 3 6 10 15 1 1 4 10 20 n=5 1 5 15 1 6 1

Binomski simboli • C(n, r) običajno označujemo z • Velja: – C(n, r) = C(n, n-r) (Pravilo enakosti!) – C(n, r) = (n/r) C(n-1, r-1) – C(n, r) = ((n-r+1)/r)C(n, r-1)

Newtonov binomski obrazec • Za vsako naravno število velja: • Dokaz npr. z matematično indukcijo. • Posledici: –: –:
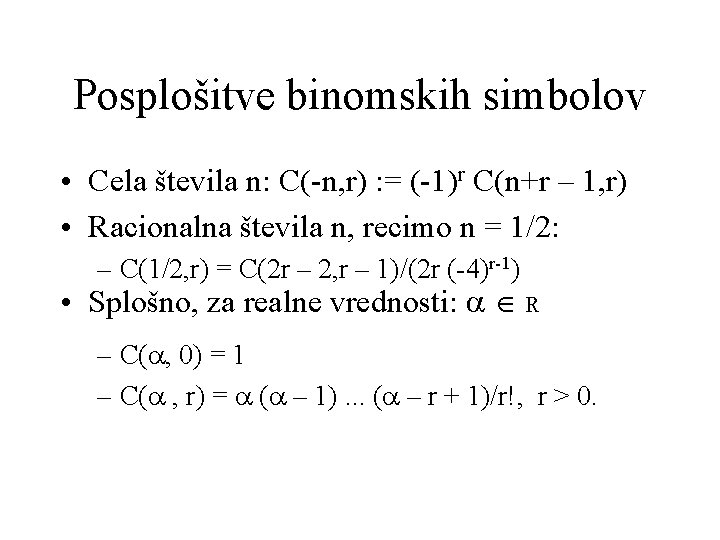
Posplošitve binomskih simbolov • Cela števila n: C(-n, r) : = (-1)r C(n+r – 1, r) • Racionalna števila n, recimo n = 1/2: – C(1/2, r) = C(2 r – 2, r – 1)/(2 r (-4)r-1) • Splošno, za realne vrednosti: a R – C(a, 0) = 1 – C(a , r) = a (a – 1). . . (a – r + 1)/r!, r > 0.

Dokažimo enakosti: • C(n, 1) + 2 C(n, 2) +. . . + n C(n, n) = n 2 n-1 (Z drugimi besedami: ) C(n, 0) + (1/2)C(n, 1)+. . . + (1/(n+1)) C(n, n) = (2 n+1 – 1)/(n+1) C(n, 0) + 2 C(n, 1) + C(n, 2) + 2 C(n, 3) +. . . = 3 2 n-1 C(n, 1) - 2 C(n, 2) - 3 C(n, 3) + 4 C(n, 4) +. . . +(-1)n n C(n, n) = 0 2 C(n, 0) + (22/2)C(n, 1) + (23/3)C(n, 2) + (24/4)C(n, 3)+. . . = (3 n+1 – 1)/(n+1) C(n, 0)2 + C(n, 1)2 +. . . + C(n, n)2 = C(2 n, n)

Metode dokazovanja identitet • • Pravilo enakosti (kombinatorični dokaz) Matematična indukcija Newtonov obrazec (odvajanje, integriranje, . . . ) Algebraična telovadba (začnemo na levi – končamo na desni) Grafična metoda – metoda poti. Metoda nedoločenih koeficientov - enakost polinomov Simbolno računanje (Npr. Mathematica) Rodovne funkcije (o tem kasneje!)

Zgled • Dokažimo, da velja: • 1 + 2 + 3 +. . . + n = n(n+1)/2

Zgled - nadaljevanje • Pravilo enakosti (kombinatorični dokaz) • Matematična indukcija • Newtonov obrazec (odvajanje, integriranje, . . . ) • Algebraična telovadba (začnemo na levi – končamo na desni) • Grafična metoda – metoda poti. • Metoda nedoločenih koeficientov - enakost polinomov • Simbolno računanje (Npr. Mathematica) • Rodovne funkcije (o tem kasneje!) • Dokažimo, da velja: • 1 + 2 + 3 +. . . + n = n(n+1)/2

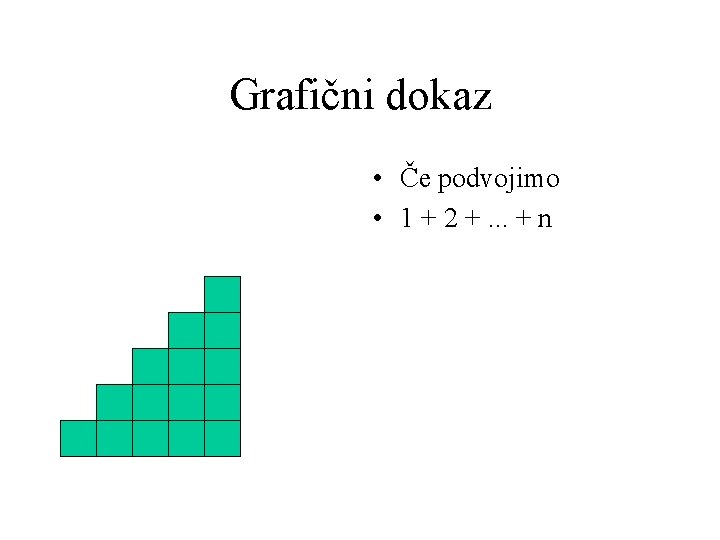
Grafični dokaz • Če podvojimo • 1 + 2 +. . . + n

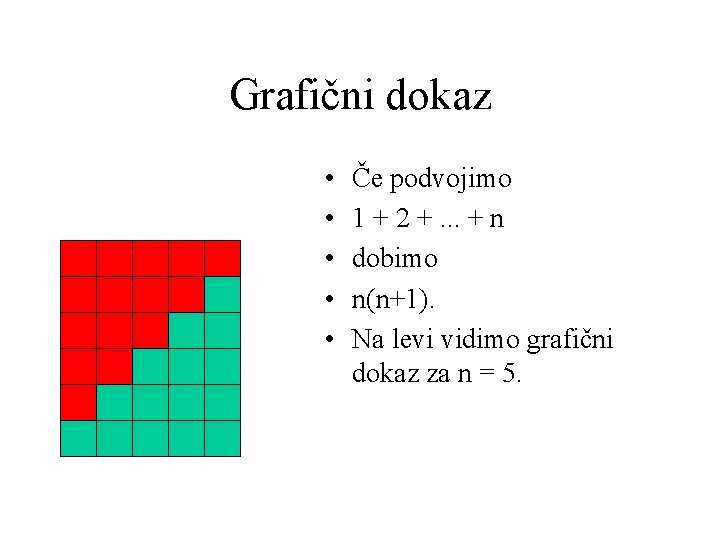
Grafični dokaz • • • Če podvojimo 1 + 2 +. . . + n dobimo n(n+1). Na levi vidimo grafični dokaz za n = 5.

Kombinacije reda r s ponavljanjem • Kombinacije reda r s ponavljanjem: C¯(A, r). • Zgled: A = {a, b, c}, r = 2. a a a b a c b a b b b c • C¯(3, 2) = (9 – 3)/2 + 3 = 6 c a c b c c

Kombinacije reda r s ponavljanjem - nadaljevanje • C¯(n, r) = C(n+r-1, r) • Naloga: imamo p znakov + in q znakov minus. Koliko nizov (dolžine p+q) lahko sestavimo? – Odg. : C(p+q, p) = C(p+q, q). Pravilo enakosti in karakteristični vektorji. • Dokaz prve vrstice s podobnim trikom.

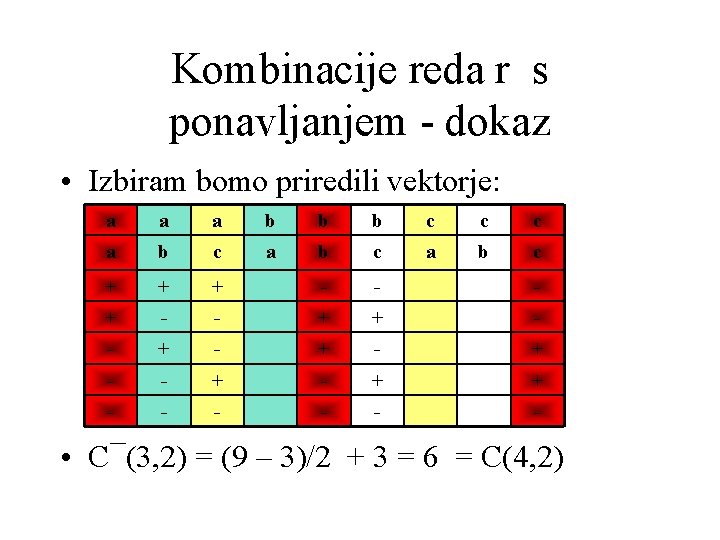
Kombinacije reda r s ponavljanjem - dokaz • Izbiram bomo priredili vektorje: a a a b b b c c c a b c + + + - - - + + - - + - + - + + - - - • C¯(3, 2) = (9 – 3)/2 + 3 = 6 = C(4, 2)

Konec dokaza • Naj bo r število znakov + in naj bo n-1 število znakov -. • [Vzeli smo n-1 in ne n, saj je zadnja vrstica vedno -] • Vsaki kombinaciji reda r s ponavljanjem lahko priredimo vektor dolžine n+r-1 sestavljen iz r znakov + in n-1 znakov -. • To prirejanje je bijekcija (pravilo enakosti).

Kombinatorika in verjetnost

Klasična (Pascalova) definicija verjetnosti • Naj bo S = {E 1, E 2, . . . , En} popoln sistem ‘enakoverjetnih’ dogodkov in A poljuben dogodek (A µ S). • Verjetnost P(A) dogodka A je definirana: • P(A) : = (število ugodnih izidov = izidov, ki sestavljajo A)/(število vseh izidov = n) = |A|/|S|. • Kombinatorični nalogi: • Določi |S| = n • Določi |A| = k.

Zgledi: • Vržemo običajno kocko. Kolikšna je verjetnost, da pade število, ki je deljivo s 3? • Iz kupa običajnih kart potegnemo naključno dve karti? Kolikšna je verjetnost, da sta obe rdeči (srce ali karo)?

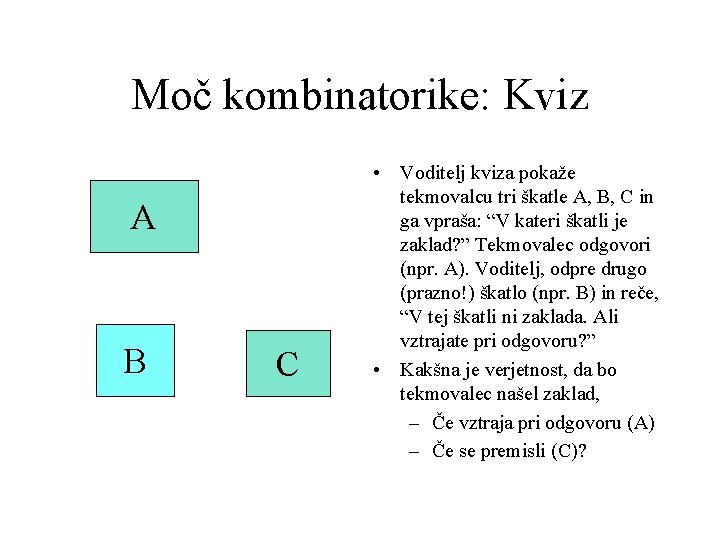
Moč kombinatorike: Kviz A B C • Voditelj kviza pokaže tekmovalcu tri škatle A, B, C in ga vpraša: “V kateri škatli je zaklad? ” Tekmovalec odgovori (npr. A). Voditelj, odpre drugo (prazno!) škatlo (npr. B) in reče, “V tej škatli ni zaklada. Ali vztrajate pri odgovoru? ” • Kakšna je verjetnost, da bo tekmovalec našel zaklad, – Če vztraja pri odgovoru (A) – Če se premisli (C)?

Moč kombinatorike – paradoks rojstnega dne. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 1. 0. 99726 0. 991796 0. 983644 0. 972864 0. 959538 0. 943764 0. 925665 0. 905376 0. 883052 0. 858859 0. 832975 0. 80559 0. 776897 0. 747099 0. 716396 0. 684992 0. 653089 0. 620881 0. 588562 0. 556312 0. 524305 0. 492703 0. 461656 0. 4313 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 0. 401759 0. 373141 0. 345539 0. 319031 0. 293684 0. 269545 0. 246652 0. 225028 0. 204683 0. 185617 0. 167818 0. 151266 0. 135932 0. 12178 0. 108768 0. 0968484 0. 0859695 0. 0760771 0. 0671146 0. 0590241 0. 0517472 0. 0452256 0. 039402 0. 0342204 0. 0296264 • Dva med Vami imata rojstni dan istega dne v letu. • Naj bo n oseb. P(n) je verjetnost, da so vsi rojstni dnevi različni. • Pri n=2: P(2) = 364/365. • Pri n=3 P(3) = 364/365 363/365. • P(n) = 365 364. . . (365 n+1)/365 n.

Porazdelitve • Iz vreče delimo elemente po celicah. Pri tem ločimo nekaj možnosti: – Ali lahko celice ostanejo prazne? – Ali ločimo med elementi? – Ali ločimo med celicami?
 Binomski adalah
Binomski adalah Kako nastane zemljevid
Kako nastane zemljevid Tatjana hodnik
Tatjana hodnik Oreh drevo
Oreh drevo Problemsko drevo
Problemsko drevo France prešeren družinsko drevo
France prešeren družinsko drevo Angleška kraljeva družina družinsko drevo
Angleška kraljeva družina družinsko drevo Jelsa drevo vlastnosti
Jelsa drevo vlastnosti Mtve
Mtve Lignin vzorec
Lignin vzorec Ima az őrangyalhoz gyerekeknek
Ima az őrangyalhoz gyerekeknek Ima jedna prekrasna planeta
Ima jedna prekrasna planeta Csca exam questions
Csca exam questions Koliko 1 dm ima cm
Koliko 1 dm ima cm Konstanta optičke rešetke
Konstanta optičke rešetke Koliko francuska ima stanovnika
Koliko francuska ima stanovnika Prirodni broj
Prirodni broj Osnovna ploskev
Osnovna ploskev Ama of a pulley
Ama of a pulley Mojca kuk
Mojca kuk Jednakokračni trapez kutovi
Jednakokračni trapez kutovi Wheel and axle mechanism
Wheel and axle mechanism Permutacija varijacija kombinacija
Permutacija varijacija kombinacija Permabilnost
Permabilnost Razlomci
Razlomci Skupina od 4 bita
Skupina od 4 bita When the ima is compared to ama in the real world, _____.
When the ima is compared to ama in the real world, _____. Ima accounting meaning
Ima accounting meaning Honda ima system
Honda ima system Ima of lever
Ima of lever Tanítás előtti ima
Tanítás előtti ima Yandex ru image
Yandex ru image Koliko kvadar ima strana
Koliko kvadar ima strana Bajt to bit
Bajt to bit Lever ima
Lever ima Aios fbs dues list
Aios fbs dues list 1 dm koliko ima cm
1 dm koliko ima cm Koliko zvezdic ima evropska zastava
Koliko zvezdic ima evropska zastava Površina piramide
Površina piramide én uram én istenem vedd el tőlem mindenem
én uram én istenem vedd el tőlem mindenem Maksimum kvadratne funkcije
Maksimum kvadratne funkcije Celinska pavza
Celinska pavza O učitelju vrati mi klikere
O učitelju vrati mi klikere