Vetaka Inteligencija Reavanje problema pretragom 1 Reavanje problema

Veštačka Inteligencija Rešavanje problema pretragom 1

Rešavanje problema pretragom Pretraga (search): Od više različitih mogućih niza radnji, koje vode u stanje sa poznatom vrednošću, treba izabrati najbolji mogući. Ulaz algoritma za pretragu je jedan problem, a izlaz je niz radnji, a to je rešenje. problem Algoritam za pretragu rešenje 2

Zadatak 7/11 USA: 7/11 supermarket Proizvodi: a, b, c, d Cena: 0. 01 $ - 7. 08 $ a + b + c + d = 7. 11 a * b * c * d = 7. 1 Prostor za pretragu: 7084 kombinacija = 2. 51*1011 Rečima: 250 milijardi kombinacija Brute force, Guess and check 7. 11 = 3 * 0. 79 = 32 * 0. 79

Zadatak 7/11 USA: 7/11 supermarket Proizvod: a, b, c, d Cena: 0. 01 $ - 7. 08 $ a + b + c + d = 7. 11 a * b * c * d = 7. 1 Prostor za pretragu: 7084 kombinacija = 2. 51*1011 Rečima: 250 milijardi kombinacija Brute force, Guess and check 7. 11 = 3 * 0. 79 = 32 * 0. 79 Rešenje: a=1. 20, b=1. 25, c=1. 50, d=3. 16

Rešavanje problema pretragom Agenti za rešavanje problema (problem solving agent) traže rešenja. Traže niz radnji koji će nas odvesti do željenog stanja. Ako su algoritmi neinformisani (uninformed), agenti ne raspolažu ni sa kakvim informacijama o problemu. Osim toga postoje još i informisane pretrage (informed). Ovi algoritmi raspolažu sa nekim znanjem o tome gde treba tražiti rešenje. 5

Agenti za rešavanje problema Inteligentni agenti žele da maksimiziraju svoje performanse. Zadatak im se uprošćava ako mogu da odrede cilj i pokušaju da taj cilj i ostvare. 6

Tipovi problema Na osnovu povezanosti agenta i njegove okoline: • • Sa jednim stanjem (single-state) (dostupna okolina) Sa više stanja (multiple-state) Poznaje uticaj svojih radnji, ali samo ograničeno može da pristupi stanjima sveta Contingency Ako okolina nije deterministička Istraživački (exploration) Ako nema nikakave informacije o uticaju svojih radnji, i treba da ”eksperimentiše” o postojećim stanjima: pretragu vrši u stvarnom svetu, a ne u modelu. 7

Dobro definisani problemi i rešenja Za definisanje problema potebno je sledećih 4 komponenti (u slučaju single-state problema): 1. Početno stanje (initial state), iz koje agent započinje pretragu. 2. Moguće radnje (actions) koje su agentu na raspolaganju. Najčešći opis koji se koristi je funkcija prelaza stanja (successor function). 8

Dobro definisani problemi i rešenja U slučaju stanja x funkcija prelaza fv(x) vraća uređen par (radnja, naknadno stanje). Prostor stanja (state space) čini jedan graf čiji su čvorovi stanja, a grane su radnje. Put (path) u prostoru stanja je jedan niz stanja koji su povezani nizom radnji. 9

Dobro definisani problemi i rešenja 3. Test cilja (goal test), koji određuje da li je dato stanje ujedno i ciljno stanje. 4. Funkcija cene puta (path cost), koji svakom putu dodeljuje jedan izdatak (koštanje). Agent za rešavanje problema će izabrati onu funkciju koštanja koji najviše odgovara njegovom kriterijumima. Radnja r koja vodi iz stanja x u stanje y ima koštanje koraka kk(x, y, r). 10

Rešenje problema (solution) je put koji vodi iz polaznog stanja u ciljno stanje. Kvalitet rešenja meri se funkcijom koštanja puta. Optimalno rešenje (optimal solution) imaće najmanje koštanje od svih putanja. 11

Definisanje problema – reprezentacija prostora stanja § Za reprezentaciju jednog problema treba potražiti konačan broj karakteristika ili osobina koji taj problem opisuju, i koji smatramo važnim za rešavanje (npr. boja, težina, dimenzija, cena, položaj, itd. ). § Ako na primer ove karakteristike redom obeležimo sa vrednostima h 1 , . . . , hn, tada kažemo da je problem sveta određen stanjem vektora (h 1 , . . . , hn). § Ako mogući skup i-te karakteristike obeležimo sa Hi, onda su stanja problema sveta elementi skupa H 1×H 2×…. . ×Hn. 12

Definisanje problema – reprezentacija prostora stanja • U toku rešavanja problema, počev od početnog stanja, menjaćemo stanja problema sveta, dok na kraju ne dođemo u neko nama odgovarajuće ciljno stanje. • Funkcije koje opisuju promene stanja nazivamo operatorima. Naravno, ne može se svaki operator primeniti na svako stanje, zato se oblast definisanosti operatora (kao funkcije) obično zadaje preko preduslova primene operatora. 13

Definisanje problema – reprezentacija prostora stanja Primer : problem 8 kraljica § Postaviti na šahovsku tablu 8 kraljica tako da se međusobno ne napadaju. Jedno moguće rešenje: § § Uopštimo zadatak na šahovsku tablu dimenzija Nx. N (N≥ 1), na kojoj treba postaviti N kraljica. Promenljiva N će biti zadata kao konstanta van prostora stanja. 14

Definisanje problema – reprezentacija prostora stanja Osnovna ideja reprezentacije prostora stanja je sledeća: Najpre u 1. vrstu stavimo jednu kraljicu, pa nakon toga u 2. vrstu stavimo kraljicu tako da se ne napada sa kraljicom koja je u prvoj vrsti. Na ovaj način u i-tom koraku stavljamo kraljicu u i-tu vrstu tako da se ne napada sa kraljicama koje smo postavili u prvih i-1 koraka. 15

Definisanje problema – reprezentacija prostora stanja Skup stanja: § U stanjima čuvamo položaje pojedinih kraljica unutar vrste. Ako u datu vrstu još nismo stavili kraljicu, tada u vektoru na tom mestu treba da stoji 0. § Osim toga u stanjima čuvamo i podatak u koju vrstu stavljamo sledeću kraljicu. § Dakle: A={(a 1 , a 2 , …. , a. N , s) | 0 ≤ ai ≤ N , 1 ≤ s ≤ N+1)} § Vrednost indeksa vrste s na mestu N+1 je nepostojeći, koji dozvoljavamo samo kako bismo proverili izlazne uslov iz algoritma. 16

Definisanje problema – reprezentacija prostora stanja Početno stanje: § Šahovska tabla je na početku prazna. Početno stanje je: k=(0, 0 , …. , 0 , 1) Skup ciljnih stanja: Imamo više ciljnih stanja. Ako promenljiva s ima vrednost nepostojeće vrste, našli smo rešenje. § Skup ciljnih stanja je: § C={(a 1 , …. . , a. N , N +1) A} 17

Definisanje problema – reprezentacija prostora stanja Skup operatora: § Naši operatori će opisivati postavljanje kraljice u vrstu s. Operatori čekaju samo na jedan ulazni podatak: indeks kolone u koju stavljaju kraljicu u vrsti s. O={stavii | 1≤ i ≤ 8} 18

Definisanje problema – reprezentacija prostora stanja Preduslov za primenu: § Kada se operator stavii može primeniti na stanje (a 1 , …, a 8 , s)? § Onda, ako se kraljica koja se stavlja: • nije u istoj vrsti ni sa jednom ranije stavljenom kraljicom. To jest: u slučaju m < s : am≠i 19

Definisanje problema – reprezentacija prostora stanja • Dijagonalno ne napada nijednu ranije postavljenu kraljicu. Dijagonalne napade najlakše možemo proveriti tako što uzmemo razliku apsolutnih vrednosti indeksa vrsta dve posmatrane kraljice, i uporedimo sa razlikom apsolutnih vrednosti indeksa kolona. Ako su ove dve vrednosti jednake, tada se dve kraljice napadaju. Kraljica koju trenutno stavljamo ima indeks vrste s, i indeks kolone i. To jest: za svako m < s : | s−m|≠|i−am| 20

Definisanje problema – reprezentacija prostora stanja Dakle, primena operatora stavii je preduslov za stanje (a 1 , …, a 8 , s): gde je 1≤ m ≤ 8 21

Definisanje problema – reprezentacija prostora stanja Funkcija primene: § § Zadajemo koje stanje (a'1 , …, a'8 , s' ) će operator stavii proizvesti od stanja (a 1 , …, a 8 , s). U novom stanju treba promeniti samo sledeće: • • § U element s stanja upišemo i, i Vrednost s povećamo za 1. Dakle: je: stavii (a 1 , …. , a 8 , s)=(a'1 , …. , a'8 , s' ) , gde a 'm = { i , ako je m=s am , inače s ' = s+1 22
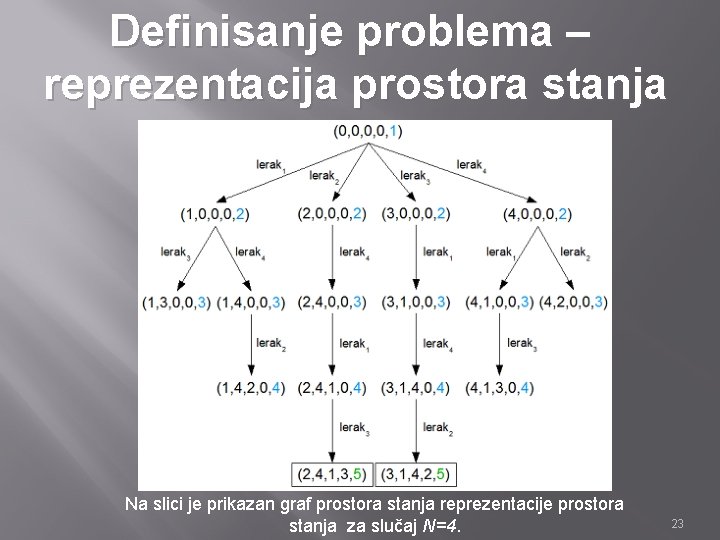
Definisanje problema – reprezentacija prostora stanja Na slici je prikazan graf prostora stanja reprezentacije prostora stanja za slučaj N=4. 23

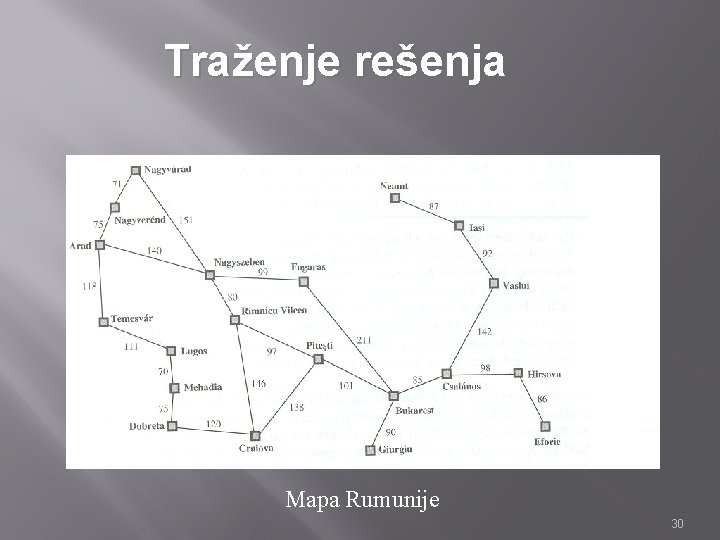
Traženje rešenja pomoću stabla za pretragu Neka naš agent bude u rumunskom gradu Arad pri kraju obilaska Rumunije. Želje agenta su: da pocrni, da nauči rumunski, da poseti istorijske znamenitosti, da uveče izlazi, da izbegava mamurluk, itd. Agent ima jednu avionsku kartu Bukurešt – npr. Pariz za sledeći dan. Razuman cilj je da stigne do Bukurešta. Svaki cilj koji ne omogućava agentu da stigne do Bukurešta može da se ostavi po strani. Tako da su radnje agenta veoma ograničene. 24

Traženje rešenja pomoću stabla za pretragu Mapa Rumunije. Cilj agenta je da stigne od Arad-a do Bukurešt-a

Traženje rešenja pomoću stabla za pretragu § § Početno stanje : u (Arad) Funkcije prelaza stanja: idi (Nagyszeben), u (Nagyszeben) • idi (Temesvár), u (Temesvár) • idi (Nagyzerénd), u (Nagyzerénd) • § § Ciljno stanje: u (Bukurest) Cena puta: za agenta koji žuri u Bukurešt najbitnije je da stigne što pre. Cena puta mogla bi da bude udaljenost pojedinih gradova od Bukurešta izražena u kilometrima (km). 26

Traženje rešenja pomoću stabla za pretragu • Prethodno definisanje nije uzimalo u obzir dosta aspekata sveta (sa kim putujemo, kakav je vidik, da li ima policije pored puta, šta prenosi radio, kakvo je vreme, kakvo je stanje puta, itd). • Ove detalje smo izostavili iz opisa stanja. Zanemarivanje pojedinih detalja iz reprezentacije naziva se apstrakcija (abstraction). 27

Apstrakcija radnji • Osim detalja okoline, treba apstrahovati i radnje. Prilikom vožnje menja se položaj agenta i vozila, troši se gorivo, zagađuje se okolina. • Mi uzimamo u obzir samo promenu položaja. Mnoge radnje ne razmatramo (uključivanje radija, gledanje kroz prozor, ili „okreni volan za 3 stepena”). 28

Traženje rešenja • Nakon što smo definisali problem, nalaženje rešenja vrši se pretragom prostora stanja. • Stabla za pretragu (search tree) se generišu na osnovu početnog stanja i funkcije prelaza stanja. • Ako se do nekog stanja može stići na više načina, onda se radi o grafu za pretragu. 29
Traženje rešenja Mapa Rumunije 30
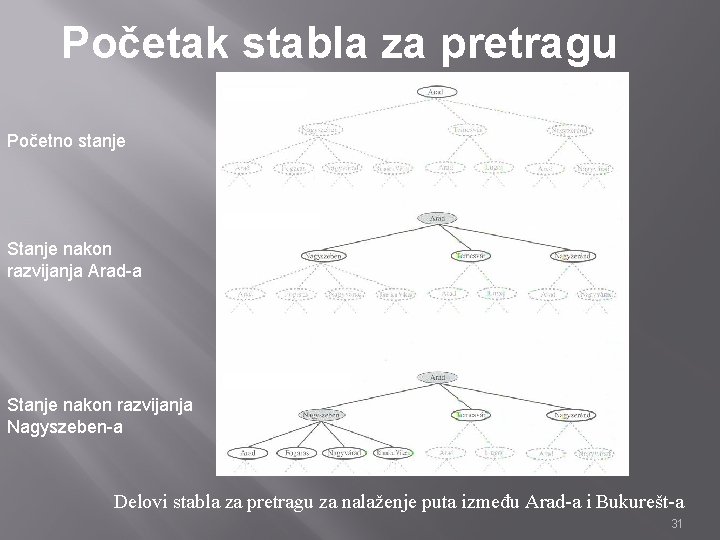
Početak stabla za pretragu Početno stanje Stanje nakon razvijanja Arad-a Stanje nakon razvijanja Nagyszeben-a Delovi stabla za pretragu za nalaženje puta između Arad-a i Bukurešt-a 31

Stablo za pretragu • Koren stabla za pretragu je onaj čvor (search node) koji odgovara početnom stanju u(Arad). • U prvom koraku treba ispitati da li je ovo ciljno stanje (put od Arad-a do Arad-a). • Ako rešenje postoji, ciljno stanje je jedan od listova stabla. • Razvijanje stanja: određivanje svih stanja koji su dostupni iz nekog stanja u samo jednom koraku. 32

Stablo za pretragu • Pretraga se vrši razvijanjem aktuelnog stanja tako što (generating) novi skup stanja. (expanding) generišemo • Moramo pamtiti i već generisane čvorove koji čekaju na razvijanje: ovu listu nazivamo obodom (fringe) ili talasnim frontom (frontier). • Svaki element oboda je čvor-list (leaf-node), koji u stablu nema potomke. 33

Stablo za pretragu Sada dobijamo tri nova stanja: u (Nagyszeben) • u (Temesvár) • u (Nagyzerénd) • Koji put ćemo da izaberemo? Suština pretrage je da izaberemo jedan put, a ostale mogućnosti ostavljamo za kasnije za slučaj da prva verzija ne dovede do rezultata. 34

Stablo za pretragu • Pretpostavimo da smo prvo izabrali Nagyszeben. Proverimo da il je to ciljno stanje (nije), pa ga razvijemo. • Sada dobijamo stanja u (Arad), u (Fogaras), u (Nagyvárad) i u (Rimnicu Vilcea). • Pretragu nastavljamo sve do trenutka dok ne nađemo rešenje, ili dok ne potrošimo sva stanja za razvijanje. 35

Stablo za pretragu 36

Prostor stanja vs. Stablo za pretragu • • • U slučaju mape Rumunije prostor stanja se sastojao od svega 20 stanja. Svakom gradu pripada jedno stanje. Međutim, u ovom prostoru stanja ima beskonačno mnogo puteva, tako da se stablo za pretragu sastoji od beskonačno mnogo čvorova. Npr. Arad-Nagyszeben, Arad-Nagyszeben. Arad, Arad-Nagyszeben-Arad-Nagyszeben. Dobar algoritam za pretragu neće pratiti ovakav put. 37

Čvorovi Čvor je struktura podataka koja se sastoji od 5 delova: Stanje. To je stanje koje pripada datom čvoru. Čvor roditelj: onaj čvor stabla za pretragu koji je generisao dati čvor. Radnja: radnja koja je izvršena nad roditeljem čvora. Cena puta: cena koštanja puta od početnog stanja do datog čvora. Dubina: broj koraka u toku puta od početnog stanja. 38

Čvor vs. stanje • Čvor je jedna struktura podatka koji koristimo kod opisivanja stabla za pretragu. • Stanje je jedna od mogućih konfiguracija sveta. • Može se desiti da dva različita čvora sadrže isto stanje. 39

Evaluacija pretrage • • Potpunost (completeness): algoritam će garantovano pronaći rešenje ukoliko ono postoji. Optimalnost (optimality): strategija će pronaći optimalno rešenje (najmanja cena koštanja). Vremenska kompleksnost (time complexity): koliko vremena će trajati pronalaženje rešenja? Prostorna kompleksnost (space complexity): koliko memorije je potrebno za izvršenje pretrage? 40

Ne-informisani postupci pretrage • • Ne-informisani postupci pretrage mogu se oslanjati samo na informacije koje su sadržane u definiciji problema. Pojedine metode pretrage razlikuju se samo po redosledu razvijanja čvorova koji čekaju na razvijanje: Pretraga u širinu, (Breadth-first search) Pretraga sa uniformnim koštanjem, (Uniform-cost search) Pretraga u dubinu, (Depth-first search) Pretraga sa ograničenom dubinom, (Depth-limited search) Pretraga sa iterativnom povećavanjem dubine (Iterative deepening search) Dvosmerna pretraga (Bidirectional search). 41

Pretraga u širinu (breadth first) Pretraga u širinu je jednostavna strategija za pretragu gde prvo razvijamo koren stabla, u sledećem koraku razvijamo naslednike korena, pa njihove naslednike, itd. Strategija pretrage razvija čvor na datoj dubini pre nego što se razvije bilo koji čvor na nižem nivou. 42

Pretraga u širinu (breadth first) • • Pretraga u širinu na jednostavnom binarnom stablu. Ova pretraga je potpuna. Ako je ciljni čvor na najnižoj konačnoj dubini d, pretraga u širinu će ga pronaći razvijajući sve čvorove koji imaju manju dubinu od njega (ukoliko je faktor grananja b manji od beskonačno). Ciljni čvor sa najmanjom dubinom nije uvek optimalan (zavisi od cene pojedinih putanja). 43

Pretraga u širinu (breadth first) Kolika su vremenska i prostorna kompleksnost ? Pretpostavimo da razvijanjem svakog stanja nastaje b novih stanja. Koren stabla generiše b čvorova na prvom nivou, od kojih svaki generiše još po b (ukupno b 2) na drugom nivou. Na trećem nivou se generiše b 3 čvorova i tako dalje. 44

Pretraga u širinu (breadth first) • Ako je rešenje na dubini d, u najgorem slučaju na d-tom nivou treba razviti sve čvorove osim poslednjeg (jer se cilj ne razvija), tako razvijajući b(d+1)-b čvorova na nivou (d+1). Broj generisanih čvorova je: b+b 2+b 3+. . . +bd+b(d+1)-b=O(b(d+1)) 45

Pretraga u širinu (breadth first) • Svaki generisani čvor treba skladištiti u memoriji jer je ili element oboda ili je predak od čvora oboda. • Ova kompleknost je eksponencijalna. • Pretpostavimo da u jednoj sekundi generišemo 10000 čvorova, a za skladištenje jednog čvora potrebno je 1000 bajtova. 46

Pretraga u širinu (breadth first) Vremenska i prostorna kompleksnost pretrage u širinu • • Prostorna kompleksnost je veći problem od vremenske kompleksnosti, ali je vreme i dalje važan faktor. Od problema sa eksponencijalnom kompleksnošću u realnom vremenu se mogu 47 rešiti samo najmanji primeri.

Pretraga sa uniformnim koštanjem (uniform cost search) • Pretraga u širinu je optimalna ukoliko je cena svakog koraka jednaka, jer se svaki put razvija nerazvijeni čvor sa najmanjom dubinom. • Pretraga sa uniformnom cenom (uniform cost search) uvek razvija n čvorova sa najmanjim koštanjem, a ne čvor sa najmanjom dubinom. • Pretraga u širinu je pretraga sa uniformnim koštanjem ako svaki korak ima istu cenu. 48

Pretraga sa uniformnim koštanjem (uniform cost search) • Ova metoda pretrage se ne bavi time od koliko koraka se sastoji određeni put, zanima ga samo ukupan trošak. • Uvek dolazi u beskonačnu petlju ako razvijanje jednog čvora vodi do radnje koja ima nultu cenu puta i vraća se u isto stanje. • Potpunost možemo garantovati samo tako je koštanje svakog koraka veće od jedne male konstante epsilon. koštanje koraka ≥ ε 49

Pretraga sa uniformnim koštanjem (uniform cost search) • • • To opet znači da koštanje puta duž puta uvek raste. Prvi nađeni ciljni čvor ujedno je i optimalno rešenje. Ovom pretragom ne upravlja dubina, nego koštanje puta, zato je teško izraziti kompleksnost u funkciji b i d. Neka je C* koštanje optimalnog puta, i neka je koštanje svake radnje bar ε. U najgorem slučaju vremenska i prostorna kompleksnost je O(b(1+C*/ε)), što može da bude više nego bd. Ova pretraga može da pretraži velika stabla sa malm i jeftinim koracima (što često i čini) pre pronalaženja velikih i korisnih puteva. 50

Pretraga po dubini (depth first search) Pretraga po dubini (depth first esarch) uvek razvija čvor sa najvećom dubinom stabla za pretragu. 51

Pretraga po dubini (depth first search) Pretraga odmah stiže na najdublji nivo, gde čvorovi više nemaju potomke. Nakon razvoja izlaze iz oboda i pretraga se vraća do najdubljeg čvora koji još ima nerazvijene potomke. 52

Pretraga po dubini (depth first search) Dubinska pretraga ima malo prostorno zauzeće. Treba da skladišti samo jedan put koji vodi od korena do lista, i duž puta i nerazvijene usputne čvorove. Jedan već razvijeni čvor može i da se briše ukoliko su svi njegovi potomci ispitani. Ako je faktor grananja b, a maksimalna dubina m, tada je prostorno zauzeće bm+1. U slučaju dubine d=12 pretraga bi zahtevala 118 kbajta u odnosu na 10 Pbajta kod širinske pretrage (redukcija od 10 milijardi puta). 53

Pretraga po dubini (depth first search) Jedna varijanta dubinske pretrage je i pretraga sa korakom unazad (backtracking search). U toj varijanti umesto svih naslednika generišemo samo jedan. Svaki samo delimično razvijeni čvor se seća koji potomak dolazi sledeći na red. Tada je umesto O(bm) potrebno samo O(m) memorije. 54

Pretraga po dubini (depth first search) Nedostatak je da sa jednim lošim izborom pretraga može da zapne duž jednog (možda beskonačnog) puta, a drugi izbor bi doveo do rešenja koji je blizu korena stabla. Stablo sa prethodne slike prvo razvija levo podstablo, iako je rešenje čvor C. Ako bi i čvor J bio rešenje, algoritam bi njega označio kao rešenje, tako da algoritam nije optimalan. U slučaju da je levo podstablo beskonačno duboko i da ne sadrži rešenje, pretraga u dubinu se nika ne bi završila, tako da ova pretraga nije potpuna. 55

Pretraga sa ograničenom dubinom (depth limited search) • • • Dubinska pretraga prevazilazi problem beskonačnog stabla tako što za maksimalnu dubinu daje jedno ograničenje l. Za čvorove na dubini l smatra da nemaju potomke. Naziv metode je pretraga sa ograničenom dubinom (POD), ili (depth limited search, DLS). Ograničenje dubine rešava problem beskonačnog puta, ali uvodi novi izvor nepotpunosti ako izaberemo l<d, to jest kad je najplići čvor (rešenje) iza granice dubine. Pretraga nije optimalna za l>d. 56

Pretraga sa ograničenom dubinom (depth limited search) Vremenska kompleksnost pretrage je O(bl), a prostorna kompleksnost je O(bl). Dubinska pretraga se može smatrati takvom specijalnom pretragom sa ograničenom dubinom gde je l=beskonačno. Ograničenje dubine se ponekad može bazirati na poznavanju problema. Na primer, na mapi Rumunije se vide 20 gradova, tako da ako znamo da rešenje postoji, ono maksimalno može biti dužine 19, tako da je l=19 jedno moguće ograničenje. 57

Pretraga sa ograničenom dubinom (depth limited search) Međutim, ako bolje pogledamo mapu, vidimo da se do svakog grada može stići u maksimalnih 9 koraka. Ovaj broj nazivamo prečnikom (dijametar) prostora pretrage. 58

Pretraga sa iterativnim povećanjem dubine (iterative deepening search) • • • Ovaj metod je jedna osnovna strategija (iterative deepening search) koji se veoma često koristi zajedno sa dubinskom pretragom za pronalaženje najboljeg ograničenja za dubinu. Algoritam postepeno povećava ograničenje dubine (0, 1, 2, . . . ) dok se cilj ne pronađe. To će se desiti kad ograničenje dubine stigne do d, najpliću dubinu ciljnog čvora. Pretraga sa iterativnim povećanjem dubine spaja prednosti širinske i dubinske pretrage. 59

Pretraga sa iterativnim povećanjem dubine (iterative deepening search) • Slično kao i kod dubinske pretrage memorijski zahtevi su veoma skromni, svega O(bd). Ako je faktor grananja konačan, pretraga je potpuna kao i širinska pretraga. • Pretraga je optimalna ako je cena puta neopadajuća funkcija dubine čvorova. 60

Pretraga sa iterativnim povećanjem dubine (iterative deepening search) • Ovaj algoritam može se činiti rasipničkim jer mnogo stanja razvija više puta. Čvorove na najvećoj dubini (d) razvijamo samo jednom, čvorove na jednom višem nivou razvijamo dva puta, i tako dalje. Sve do potomaka korena koje razvijamo d puta. Ukupan broj razvijenih čvorova je: Č(IPD)=(d)b+(d-1)b 2+. . . +(1)bd • To je vremenska kompleknost bd. 61

Pretraga sa iterativnim povećanjem dubine (iterative deepening search) Prve 4 iteracije pretrage na binarnom stablu, gde algoritam pronalazi rešenje u četvrtoj iteraciji. 62

Pretraga sa iterativnim povećanjem dubine (iterative deepening search) • Generisani broj čvorova kod širinske pretrage je: Č(ŠP)=b+b 2+. . . +bd+b(d+1)-b • Ako je b=10 i d=5: Č(IPD)=50+400+3000+20000+100000+123450 Č(ŠP)=10+1000+100000+999990 =1111100 • Ako je prostor za pretragu velik, i ako dubina na kojoj se nalazi rešenje nije poznato, preporučuje se pretraga sa iterativnim povećanjem dubine. 63

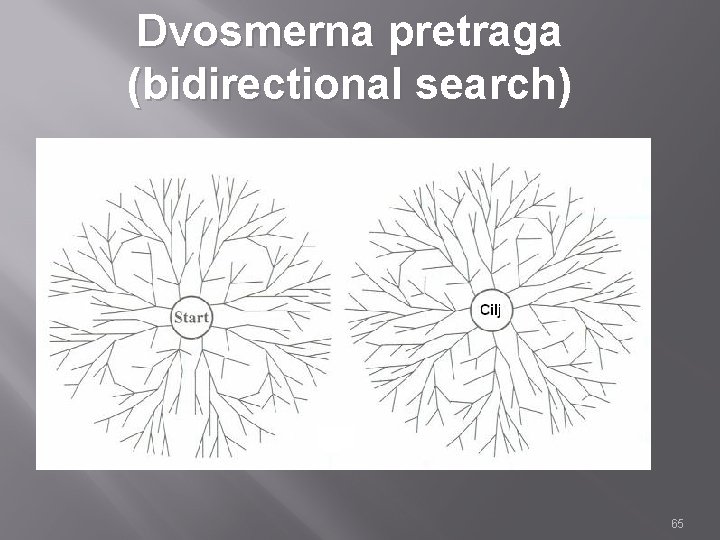
Dvosmerna pretraga (bidirectional search) Ideja je da istovremeno pokrenemo jednu pretragu unapred iz početnog stanja i jednu pretragu unazad iz ciljnog stanja, a pretraga se završava kad se dva stanja negde susretnu. Rezonovanje je da je b(d/2)+b(d/2) mnogo manje od bd, to jest na slici zbir površine dva kruga je manji od površine kruga čiji je centar početno stanje, i koji sa obodom dotiče ciljno stanje.
Dvosmerna pretraga (bidirectional search) 65

Kraj 66
- Slides: 66