Vetaka Inteligencija Neuralne mree 2 deo 1 Modeli

Veštačka Inteligencija Neuralne mreže 2. deo 1

Modeli veštačkih neurona Model neurona sastoji se iz sledeća tri elementa: 1. Skup sinapsi kojim su neuroni međusobno povezani. Svakoj sinapsi je pridružen težinski koeficijent. Za proizvoljni k-ti neuron oznaka wkj označava težinski koeficijent na njegovoj j-toj sinapsi. To znači da se j-ti ulaz xj u k-ti neuron, prethodno množi sa adekvatnim težinskim koeficijentom wkj. U slučaju negativne vrednosti wkj radi se o inhibicionoj sinapsi, u suprotnom, sinapsa je eksitaciona. 2

Modeli veštačkih neurona 2. Sumator ulaznih signala prethodno pomnoženih sa odgovarajućim težinama sinapsi. Ovaj element se naziva još i linearni kombinator, a njegov ozlaz predstavlja aktivaciju neurona ili nivo aktivacije neurona. 3. Aktivaciona funkcija kojom se ograničavaju vrednosti izlaza neurona. Opseg izlaza neurona obično se kreće u intervalu [0, 1] ili [-1, 1]. 3

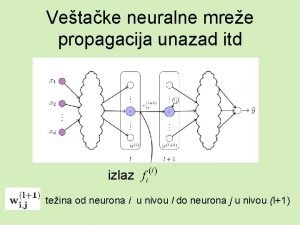
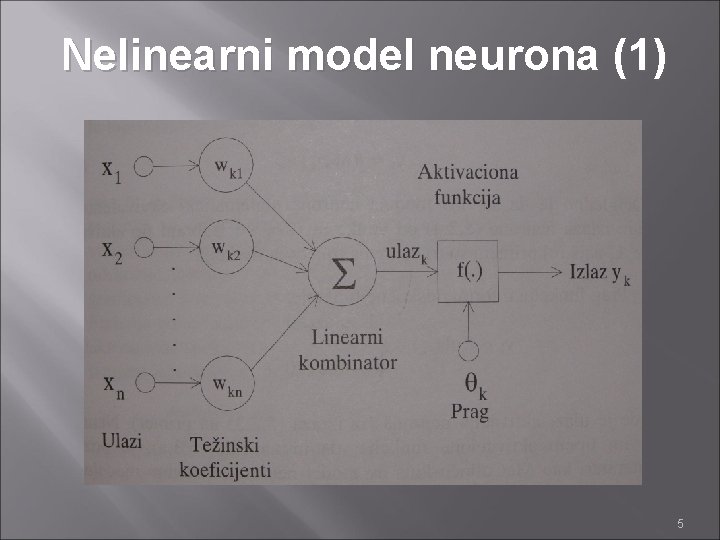
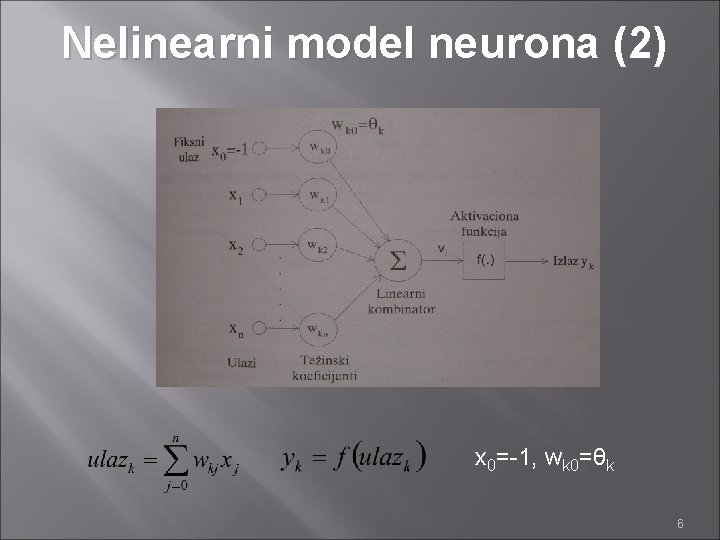
Modeli veštačkih neurona Neuron može sadržati i prag θ čiji je zadatak da ograniči nivo aktivacije neurona. Matematički opis neurona sastoji se iz dve jednačine: x 1, x 2, . . . , xn - ulazni signali wk 1, wk 2, . . . , wkn - težinski koeficijenti sinapsi k-tog neurona ulazk – linearna kombinacija ulaza Θk – prag k-tog neurona f( • ) – aktivaciona funkcija neurona yk – izlazni signal k-tog neurona 4

Nelinearni model neurona (1) 5

Nelinearni model neurona (2) x 0=-1, wk 0=θk 6

Aktivacione funkcije Za ponašanje izlaza neurona od velike je važnosti izabrani tip aktivacione funkcije. U najširoj primeni su tri osnovna tipa ovih funkcija: 1. Prag funkcija u formi odskočne funkcije 2. Izlomljena linearna funkcija 3. Sigmoidalna funkcija 7

Prag funkcija f(. ) 1 ulaz Izlaz neurona je 1 u slučaju nenegativne aktivacije neurona, u suprotnom je jednak 0. 8

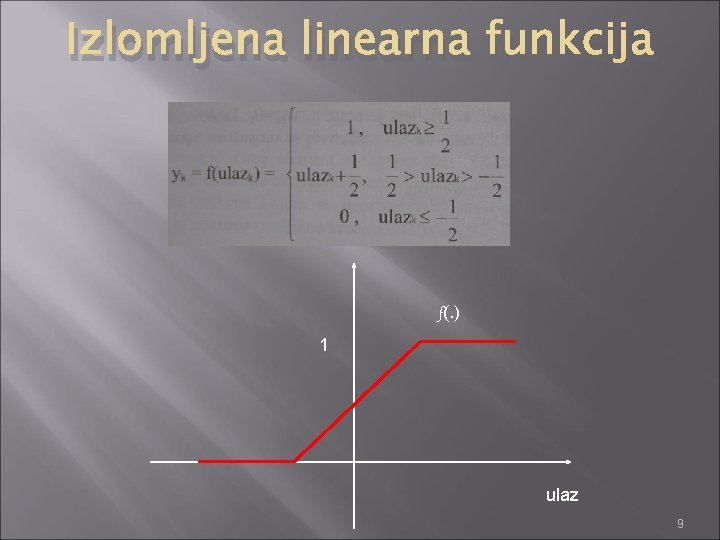
Izlomljena linearna funkcija f(. ) 1 ulaz 9

Sigmoidalna funkcija je nelinearna, diferencijabilna funkcija. Ovo je najčešći tip aktivacione funkcije neurona. Monotono je rastuća, glatka i teži ka asimptotama. Formula sigmoidalne funkcije: f(. ) 1 ulaz Parametar a određuje nagib funkcije. Za veliko a funkcija teži formi jedinične odskočne funkcije. Ovo je unipolarna sigmoidalna funkcija (interval (0, 1)) 10

Sigmoidalna funkcija Ako želimo da izlaz aktivacione funkcije bude u granicama (-1, 1), možemo koristiti tangens hiperboličnu funkciju: f(. ) 1 ulaz -1 11

Arhitekture veštačkih neuralnih mreža Načini povezivanja neurona određuju tip arhitekture veštačke neuronske mreže. Mreže se mogu podeliti u pet klasa: 1. 2. 3. 4. 5. Jednoslojne Višeslojne Rekurentne Bočno povezane Hibridne 12

Jednoslojne mreže Svi neuroni su organizovani u jedan procesni sloj neurona. Ovaj sloj ujedno predstavlja i izlazni sloj mreže. Mreža ima i ulazni sloj koji služi za prihvatanje ulaznih podataka. Nema veza unutar sloja. 13

Višeslojne mreže Kao i kod jednoslojnih, višeslojne mreže sadrže ulazni sloj za prijem podataka i izlazni sloj. Međutim, kod višeslojnih mreža mogu se pojaviti jedan ili više skrivenih slojeva koji nemaju vezu sa ulazom i sa izlazom. Ove mreže mogu biti potpuno ili delimično povezane. 14

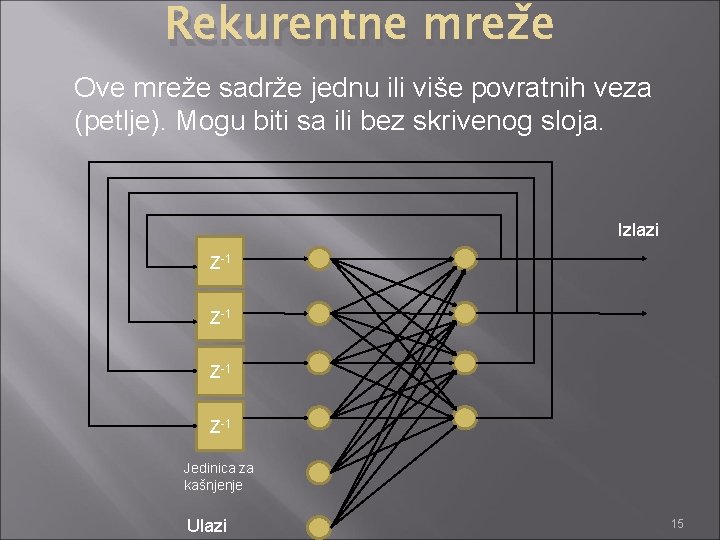
Rekurentne mreže Ove mreže sadrže jednu ili više povratnih veza (petlje). Mogu biti sa ili bez skrivenog sloja. Izlazi Z-1 Z-1 Jedinica za kašnjenje Ulazi 15

Bočno povezane mreže Ovaj tip mreže pored ulaznog i izlaznog sloja sadrži međusloj sa neuronima. Neuroni ovog sloja su povezani sa njima susednim neuronima (bočno povezivanje neurona). 16

Hibridne mreže Ove mreže se formiraju kombinovanjem osnovnih osobina dva ili tri tipa ranije navedenih arhitektura. 17

Obuka veštačkih neuronskih mreža Da bi se izvršila aproksimacija funkcije, klasifikacija uzoraka, estimacija parametara ili rešio neki drugi problem pomoću neuralnih mreža, potrebno je dati problem postaviti u formi skupa primera-uzoraka, koji se naziva obučavajući skup. Ako je svakom dovedenom ulaznom vektoru x pridružen i vektor željenih izlaza d, onda se metod podešavanja težina sinapsi naziva obuka sa nadzorom (supervised learning/training). 18

Obuka veštačkih neuronskih mreža Ako je dat samo ulazni vektor i struktura mreže se samopodešava, onda se radi o obuci bez nadzora (unsupervised learning/training). Pored ove dve metode, postoje i druge, manje poznate metode podučavanja, npr. obučavanje sa kritikom (reinforcement learning). 19

Obuka sa nadzorom podrazumeva poznavanje željenog odziva d na svaki ulaz – pobudu x. Generator signala učenja (“učitelj”) doprema signal željenog izlaza d i omogućava nalaženje razlike (rastojanje ρ(d, y)) između stvarnog i željenog izlaza. Na osnovu prethodno određenog algoritma “učitelj” može da vrši korekcije težine sinapsi, tj. elemenata matrice W u cilju minimizacije tekućeg odstupanja. 20

Obuka sa nadzorom Promena parametara mreže vrši se korak po korak u cilju “emulacije” učitelja, odnosno znanje “učitelja” se prenosi neuronskoj mreži. Obuka sa nadzorom pripada grupi zadataka kao što su aproksimacione i interpolacione tehnike, regresiona analiza i estimacija parametara. 21

Kod ovog načina učenja željeni izlaz nije neposredno poznat, tako da kriterijum adaptacije mreže mogu biti samo odzivi mreže na tekuće ulazne podatke. 22

Obuka veštačkih neuronskih mreža Neuronske mreže obučene obukom sa nadzorom i mreže obučene bez nadzora bitno razlikuju. Obuka bez nadzora omogućava organizovanje složenih karakteristika sistema u različite klase, dok se obukom sa nadzorom mogu izračunati karakteristike posmatranih klasa. 23

Opšte pravilo obuke neuronskih mreža Obuka neuronskih mreža se ostvaruje putem promena težinskih koeficijenata na sinpsama. Promene na sinapsama su posledica dovođenja različitih obučavajućih uzoraka na ulaz u mrežu. Ako su pri obuci na raspolaganju i željene vrednosti izlaza, onda se radi o obuci sa nadzorom. U suprotnom, obuka se naziva obukom bez nadzora. 24

Opšte pravilo obuke neuronskih mreža Vektor težina sinapsi wi=[wi 1 wi 2 … win]T i-tog neurona menja se proporcionalno proizvodu ulaznog vektora x i signala obuke r. Signal obuke je funkcija od sinapsi wi, ulaza neurona x, a ponekad i signala željenih izlaza di, tj. r=r(wi, x, di) Promena vektora težina u diskretnom trenutku k može se definisati sa Δwi(k)=ηr(wi(k), x(k), di(k))x(k) η – konstanta obuke Ovaj izraz pokazuje zavisnost promene težina sinapsi od signala obuke i vrednosti ulaznog vektora. Pravilo obuke za diskretni slučaj može napisati kao: wi(k+1)=wi(k)+ ηr(wi(k), x(k), di(k))x(k) wi(k+1)=wi(k)+ Δwi(k) 25

Hebb-ovo pravilo obuke Ova obuka je obuka bez nadzora. Ovo je najstarije pravilo koje je definisao neuropsiholog Hebb na sledeći način: “Kad ćelija A putem aksona stalno pobuđuje ćeliju B, dolazi do intenziviranja hemijskofizičkih procesa u jednoj ili obe ćelije, što rezultuje povećanjem efikasnosti pobuđujuće ćelije A”. 26

Hebb-ovo pravilo obuke U slučaju pozitivnog proizvoda j-tog ulaza i izlaza itog neurona yixj dolazi do povećanja faktora težine sinapse wij. U suprotnom, ovaj faktor se smanjuje. Promenljive x i y predstavljaju ulaz i izlaz neurona, respektivno. Matematički se promena j-te sinapse i-tog neurona definiše sa Δwij= ηyixj, za j=1, 2, . . . , n (n je broj ulaza neurona) 27

Hebb-ovo pravilo obuke Za signal obuke usvaja se izlaz neurona r=f(wi. Tx) Pošto je r=yi, može se pisati Δwij= ηf(wi. Tx)xj Ovaj izraz prestavlja adaptaciju j-te sinapse, dok vektor adaptacije svih sinapsi i-tog neurona ima oblik Δwi= ηf(wi. Tx)x Vrednost korelacionih faktora yixj je kriterijum po kojem se vrši izbor sinapsi koje će se pojačati (yixj>0) ili smanjiti (yixj<0). 28

Perceptron pravilo obuke U ovom slučaju se radi o obuci sa nadzorom, a signal obuke se formira kao razlika između željenog i stvarnog izlaza neurona i jednak je r=di-yi yi=sgn(wi. Tx) stvarni izlaz neurona, a di je željeni izlaz i-tog neurona. Sada se promene na vektoru težina sinapsi za i-ti neuron mogu izraziti kao Δwi= η(di-sgn(wi. Tx))x Promena pojedinih sinapsi se izračunava po sledećoj formuli: Δwij= η(di-sgn(wi. Tx))xj, j=1, 2, . . . , n 29

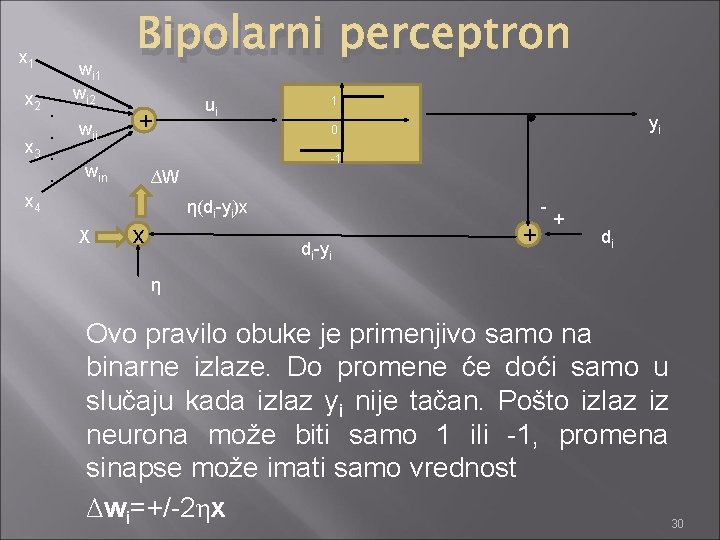
x 1 x 2 . . x 3. . x 4 wi 1 wi 2 wii Bipolarni perceptron + ui 1 yi 0 -1 win ∆W η(di-yi)x X x di-yi + + di η Ovo pravilo obuke je primenjivo samo na binarne izlaze. Do promene će doći samo u slučaju kada izlaz yi nije tačan. Pošto izlaz iz neurona može biti samo 1 ili -1, promena sinapse može imati samo vrednost Δwi=+/-2ηx 30

Bipolarni perceptron Predznak je pozitivan u slučaju kada je di=1 i sgn(w. Tx)=-1, a negativan kada je di=-1 i sgn(w. Tx)=1. Početne vrednosti težine sinapsi se mogu postaviti na proizvoljne vrednosti. 31

Delta pravilo obuke Ovaj metod se još naziva i pravilom kontinualnog perceptrona ili metod korekcije greške. Ovo je obuka sa nadzorom. Koristi se samo za neurone sa kontinualnom aktivacionom funkcijom (kontinualni perceptron). Osnovna ideja ove metode je minimizacija ciljne funkcije bazirane na signalu greške, odnosno, težnja da se stvarni izlaz iz neurona što više približi željenim vrednostima izlaza. 32

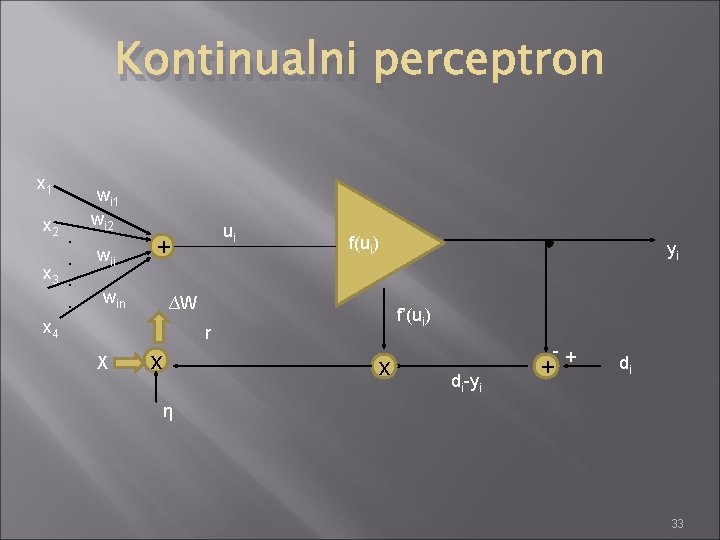
Kontinualni perceptron x 1 x 2 . . x 3. . x 4 wi 1 wi 2 wii ui + win f(ui) yi ∆W f’(ui) r X x x -+ di-yi + di η 33

Delta pravilo obuke Ciljna funkcija se formira u obliku sume kvadrata greške, pri čemu greška predstavlja razliku između željenog i stvarnog izlaza iz neurona. E=0. 5*(di-yi)2, (kriterijumska funkcija) ili E=0. 5*(di-f(wi. Tx))2 34

Delta pravilo obuke dobija se derivacijom kriterijumske funkcije po težinama sinapsi, što rezultuje sa vektorom gradijenta greške u formi: Shodno ovome, pojedine komponente ovog gradijentnog vektora su Pošto minimizacija greške zahteva da promene težinskih koeficijenata sinapsi budu u negativnom gradijentnom pravcu, biće gde je η koeficijent obuke 35

Delta pravilo obuke Signal obuke poznat po nazivu Delta signal ima oblik: Sada se promena vektora težina sinapsi, odnosno pojedinih komponenti izračunava kao: 36

Delta pravilo obuke Crtanjem ciljne funkcije u zavisnosti od promena težine na sinapsama dobila bi se multidimenzionalna površ, koja predstavlja površ greške. Zavisno od tipa korišćenih aktivacionih funkcija mogu se uočiti dve situacije. U slučaju kada se koriste linearne aktivacione funkcije, površ greške je kvadratna funkcija težine sinapsi, te površ ima jedan izražen minimum. 37

Delta pravilo obuke Kada se koriste nelinearne aktivacione funkcije, površ greške ima više minimuma. U oba slučaja cilj Delta pravila je da adekvatnim algoritmom, korak po korak, počevši od proizvoljne tačke na površi greške dostigne globalni minimum. Globalni minimum nije uvek moguće naći u slučaju prisustva nelinearnih aktivacionih funkcija, jer algoritam može prvo naići na neki lokalni minimum. Brzina i stabilnost algoritma može se podešavati sa koeficijentom obuke η. Za manje vrednosti η, proces obuke konvergira sigurno ka minimumu, ali duže traje. 38

Kraj 39