UNIVERSIT DES SCIENCES ET DE LA TECHNOLOGIE DORAN

UNIVERSITÉ DES SCIENCES ET DE LA TECHNOLOGIE D’ORAN FACULTÉS DES SCIENCES DÉPARTEMENT INFORMATIQUE Master 2 RFIA Module: Optimisation Avancée Exposé sur: Support Vector Machines Présenté par : BEKHELIFI Okba Responsable du module: PR. BENYETTOU Mohamed Année universitaire: 2012 -2013

Plan � � � � � 1. Introduction 2. Définition 3. Historique 4. Domaines d’application 5. Principes 6. Implémentation 7. Exemple d’application 8. Avantages & Inconvénient 9. Conclusion Références

1. Introduction � Face aux exigences progressives de la résolution des problèmes de classification les méthodes classiques dévoiles des limites � Besoin de nouveaux techniques et méthodes � Apparition des SVMs avec des approches différentes pour apprentissage supervisé

2. Définition � � Support Vector Machines ou maximum margin classifier Techniques d’apprentissage supervisé fondées sur la théorie d’apprentissage statistique. Application de SRM(structural risk minimization ): trouver un séparateur qui minimise la somme de l’erreur de l’apprentissage 2 notion de base: marge maximale & méthode a Kernel

3. Historique • 1974 Vapnik et Chervonenkis fondent le domaine d’apprentissage statistique. • 1979 la 1ére édition de l’ouvrage «Estimation of Dependences Based on Empirical Data” par Vapnik & Chervonenkis (en langue russe) • 1982 traduction de l’ouvrage «Estimation of Dependences Vladimir Vapnik Based on Empirical Data” en Anglais par Vapnik. • 1992 pour la COLT 92 : proposition d’utilisation de la Kernel Trick d’Aizerman par Boser, Guyon and Vapnik. • 1995 introduction du classifieur a marge souple (soft margin) par Vapnik & Cortes, la naissance officielle des SVMs. • 1998 1ére critique sur les SVMs montrant la limite de la marge dure, Bartlett and Shawe -Taylor • 2000 Démonstration des limites de la soft margin, Shawe-Taylor and Cristianini.

4. Domaines d’applications � - Reconnaissance de formes/Classification : Vision Machine: Identification de visage, reconnaissance d’expression faciale : Surpasse les approches alternatives (1. 5% taux d’erreur) [5] Reconnaissance des chiffres manuscrits: les résultats d’USPS (service de la poste des états unis) databatse comparable à la meilleure approche (1. 1% taux d’erreur) [6] Catégorisation de texte : un exemple populaire est le corpus de texte de l’agence Reuteurs qui a collecté 21450 documents d’information datant de 1997 et les a partitionnés en 135 catégories différentes. [6]

4. Domaines d’applications � Bioinformatique: prédiction de la structure des protéines, prédiction du progrès d’une maladie. [5] � Régression: estimation et prédiction des valeurs des fonctions [6] � Vers l’utilisation des SVMs pour des problèmes d’apprentissage non supervisé: Clustering , Novelty detection (détection de nouveautés)

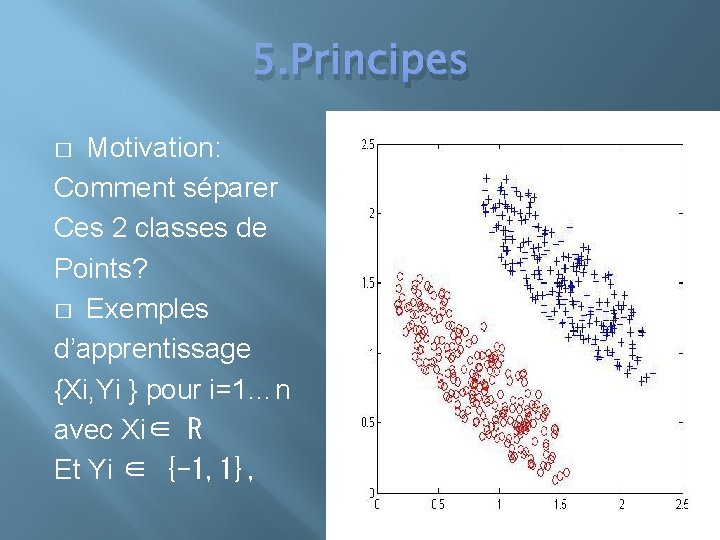
5. Principes Motivation: Comment séparer Ces 2 classes de Points? � Exemples d’apprentissage {Xi, Yi } pour i=1…n avec Xi∈ R Et Yi ∈ {-1, 1}, �

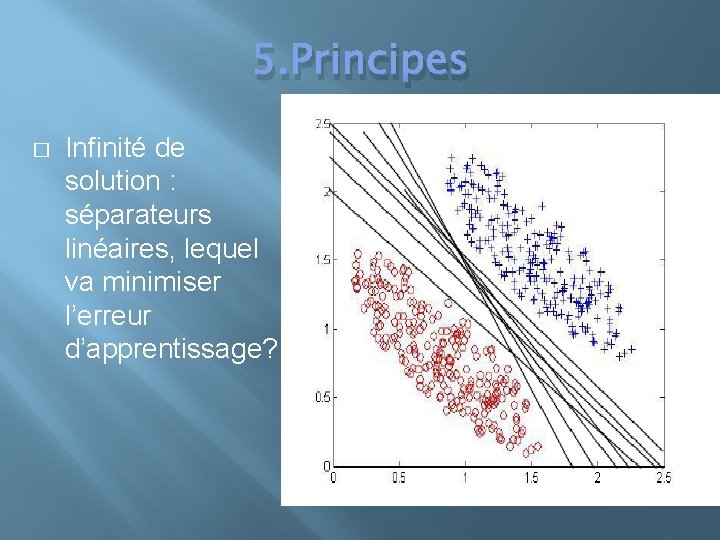
5. Principes � Infinité de solution : séparateurs linéaires, lequel va minimiser l’erreur d’apprentissage?

5. 1 Séparation par Hyperplan H : espace a dimension N Hyperplan séparateur : {x ∈ H/ <w, x>+b=0}, w ∈H, b ∈ R W: vecteur orthogonal a H b: biais (offset) (w, b) ∈ H x R sont appelé forme canonique d’hyperplan (ou hyperplan conanique) si : Pour x 1…xm ∈ H : min|<w, x>+b|=1 i=1. . m [6]

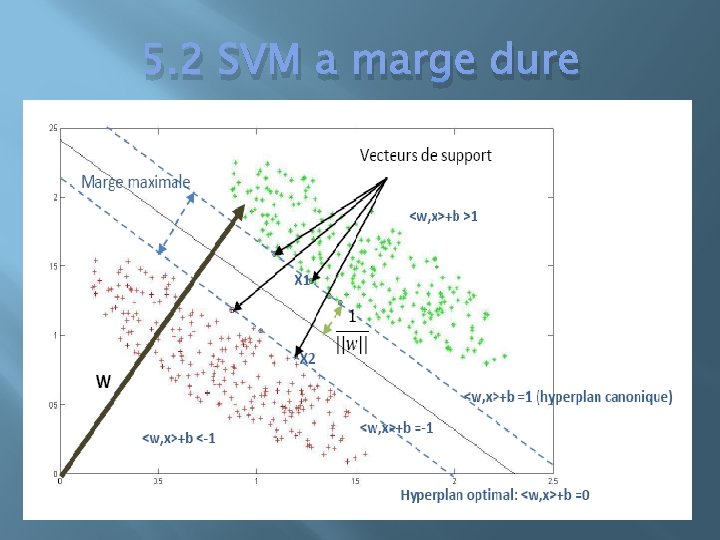
5. 2 SVM a marge dure

5. 2 SVM a marge dure Sur un espace H, pour un hyperplan {x ∈ H/ <w, x>+b=0} on appelle : Marge : ρ (x, y)=(y(<w, x>+b))/||w|| min ρ (xi, yi)=min (yi(<w, xi>+b))/||w|| Distance minimale entre l’hyperplan optimal et l’hyperplan canonique = Distance entre l’hyperplan et les points les plus proches

5. 2 SVM a marge dur Soit x 1 et x 2 deux points ∈ hyperplans canoniques respectivement <w , x 1>+b =+1 < w, x 2 >+b = -1 on déduit que : <w, (x 1 -x 2)> = 2. pour l’hyperplan séparateur: <w, x>+b=0 Le vecteur normal est: w/||w|| Distance entre x 1 -x 2 = Projection de <w, (x 1 -x 2)> sur l’hyperplan: => <w, (x 1 -x 2)> /||w|| =>2/||w|| (marge maximale) �

5. 2 SVM a marge dur Distance entre x 1 (ou x 2) et l’hyperplan optimal = 1/||w|| � Maximiser la marge => minimiser ½ ||w||² Sous contrainte yi(<w, xi>+b)>=1 i=1. . m � =>Problème d’optimisation!

5. 2 SVM a marge dur � Relaxation lagrangienne: αi: représentent les multiplicateurs de Lagrange cherchez l’extremum de L(w, b, α) Þ Calculer les dérivées selon w et b, sous conditions de KKT (Karush-Kuhn-Tucker): yi(<w, xi>+b)>=1 αi yi(<w, xi+b>)=0 αi>=0 Les données xi pour lesquels αi >0 sont appelées vecteur de support, ces points déterminent les frontières de la marge et ainsi contribuent a la détermination de l’hyperplan séparateur optimale.

5. 2 SVM a marge dur On remplace les résultat dans L(w, b, α) on obtient:

5. 2 SVM a marge dur � Le problème primal est formulé par son dual : � Trouver un séparateur linéaire optimal revient à résoudre ce problème de programmation quadratique ou les sont αi calculable est le w déduits a partir de l’équation (3).

5. 2 SVM a marge dur � On remplaçant la valeur de w de l’équation (3) dans la fonction de décision on obtient : Ce qui montre l’utilité des vecteurs à support dans la phase de généralisation, ou le x présente une donnée.

5. 2 SVM a marge dure � Les SVMs présentés traitent que des problèmes de classification linéairement séparable, en réalité les problèmes de classification sont généralement non linéairement séparables, on distingue 2 types de problèmes non linéairement séparables a 2 classes : � Une mal classification de données bruitées c. -à-d. certains exemples se trouvent à l’intérieur de la marge, l’introduction de marge souple a pour but de résoudre ce problème. [5] � les données d’apprentissage forment des nuages de points, généralement il peut y avoir un séparateur linéaire pour ce cas après un changement de dimension de l’espace, cette méthode utilise la projection vers un autre espace et le Kernel trick. [6]

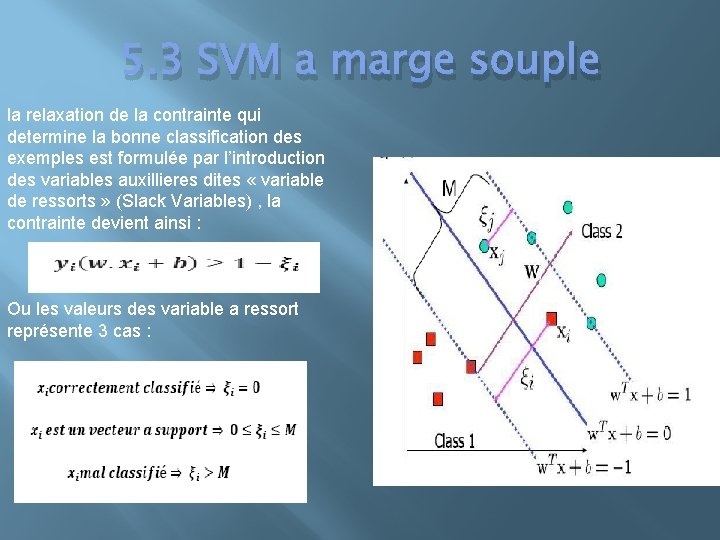
5. 3 SVM a marge souple la relaxation de la contrainte qui determine la bonne classification des exemples est formulée par l’introduction des variables auxillieres dites « variable de ressorts » (Slack Variables) , la contrainte devient ainsi : Ou les valeurs des variable a ressort représente 3 cas :

5. 3 SVM a marge souple � La fonction objective devient: � C représente une constante déterminante du compromis entre les deux objectifs opposés : la minimisation de l’erreur et la maximalisation de la marge, la sélection de C reste intuitive vue qu’aucune méthode n’a était introduite pour le faire. [6]

5. 3 SVM a marge souple � La formulation dual du problème est similaire a celle du cas linéairement séparable sauf que les multiplicateurs de Lagrenge deviennent bornés par C.

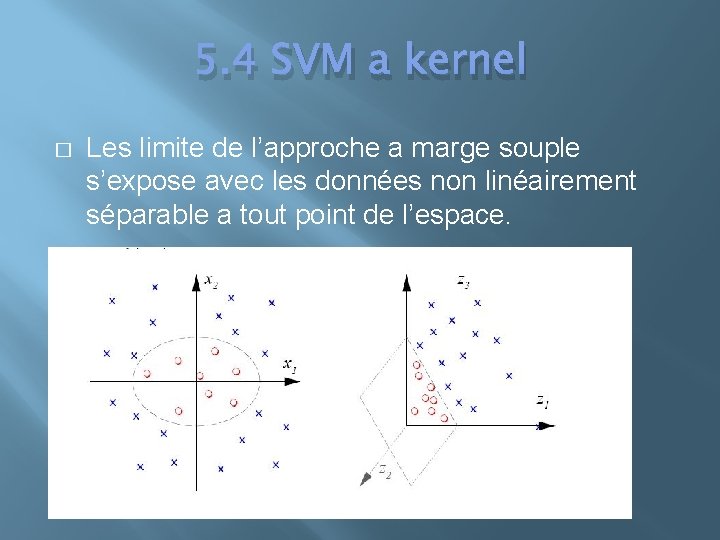
5. 4 SVM a kernel � Les limite de l’approche a marge souple s’expose avec les données non linéairement séparable a tout point de l’espace.

5. 4 SVM a Kernel � Fonction de Projection: � D’où la fonction objective du problème d’optimisation sera reformulé comme :

5. 4 SVM a Kernel � � Le produit scalaire imposé par la projection est plus complexe et très coûteux en calcul due a la grande dimension de ϕ, d’autres fonctions dites fonction Kernel peuvent réaliser ce calcul sans faire de projection explicite vers d’autres espaces, l’utilisation de fonction Kernel pour éviter la projection est connu sous le nom de « Kernel Trick » . [6] Une fonction Kernel (noyau) est définie comme :

5. 4 SVM a Kernel Pour remplacer la fonction de projection une fonction Kernel doit vérifier le théorème de Mercer qui énonce qu’une fonction Kernel représente le produit scalaire si elle est définie positive. Des exemples des fonctions Kernel : � -Noyau Polynomial de degree d : � Noyau RBF avec longueur : � Noyau Sigmoïd avec paramétres k et :

5. 4 SVM a Kernel � Avec l’aide du Kernel trick le problème d’optimisation est formulé comme :

5. 5 Classification Multi classe � La plupart des problèmes de classification sont a multi classe, les SVMs ont étaient conçu initialement pour résoudre des problèmes de classification a deux classes, en revanche d’autres méthodes ont permis l’extension des approches SVM pour traiter ce type de problème.

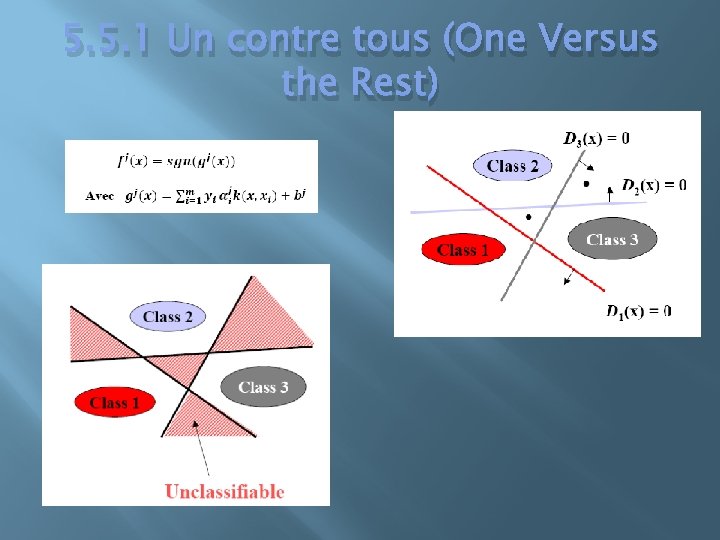
5. 5. 1 Un contre tous (One Versus the Rest)

5. 5. 2 Classification par pair (Pairewise classification) Connu sous le nom de classification un contre un (one versus one), dans cette méthode on détermine un classifieur pour chaque pair de classe, pour M classe on aura séparateurs

6. Implementation � Pour effectuer l’apprentissage d’un SVM la manière la plus simple est de résoudre le problème de programmation quadratique formulé a l’aide d’un Solver de programmation quadratique, comme étant un problème standard de la théorie d’optimisation, une variété de ressources logicielle existe pour la Programmation Quadratique (QP) (exemple : le QUADPROG de MATLAB).

6. Implementation � � � On trouve d’autres implémentations des SVMs comme package libre : -SVMlight -LIBSVM -Simple. SMV -Quelques Toolbox de Matlab comportent des implémentations des SVMs (exemple : la Tool. Box Bioinformatics)

6. 1 méthode de décompostion � Une méthode simple de décomposition appelé « méthode de chunking » commence par un sous-ensemble arbitraire de données, et résout le problème pour ses q exemples, les vecteurs a support extrait de ce sous-ensemble sont ajoutés au 2éme part de données, le processus se répète jusqu'à la détermination de tout les vecteurs a support. [5]

6. 2 Sequential Minimal Optimization (SMO) � � la décomposition permet seulement a travailler avec un ensemble de taille égale a 2, résoudre un problème programmation quadratique de taille de 2 peut se faire analytiquement, donc cette méthode évite l’utilisation d’un Solver numérique de QP, le compromis est que les pairs d’exemples optimisé de cette façon sont itéré plusieurs fois, l’exigence est que la base de l’algorithme est qu’une simple formule analytique, donc le temps d’exécution est réduit. L’avantage de cette méthode est que la dérivation et l’implémentation sont simples. [5]

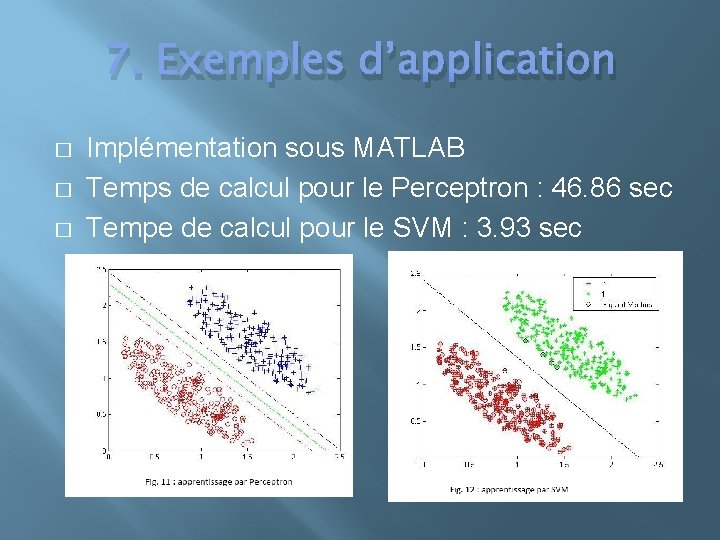
7. Exemples d’application � Notre exemple d’application des SVMs présente une comparaison entre un Perceptron et un SVM en phase d’apprentissage pour un problème de classification linéaire. � Exemple d’apprentissage : points a(x 1, x 2). Nombre d’exemples : 454 Classes : 2 désigné par +/- 1 � � � - Perceptron: 1 couche d’entrée à 2 neurones, couche de sortie un seul neurone. - Fonction de décision : tangente hyperbolique. - Algorithme d’apprentissage : Widrow-Hoff � SVM linéaire a marge dure.

7. Exemples d’application � � � Implémentation sous MATLAB Temps de calcul pour le Perceptron : 46. 86 sec Tempe de calcul pour le SVM : 3. 93 sec

8. Avantages & inconvénients Avantages: � Absence d’optimum local. � contrôle explicite du compromis entre la complexité du classifieur et l’erreur. � Possibilité d’utilisation de structure de données comme les chaines de caractères et arbres comme des entrées. � traitement des données a grandes dimensions.

8. Avantages & inconvénients Inconvénients : � Demande des données négatives & positives en même temps. � Besoin d’une bonne fonction Kernel. � Problèmes de stabilité des calculs dans la résolution de certains programme quadratique a contraintes.

9. Conclusion Les SVMs présentent un alternatif utile aux différentes méthodes de classification classique, leurs principes de vaste marge et fonction Kernel les permettent de réaliser des taux de classification et de minimisation très importants.

Références � [1] Vojislav Kecman, “Learning and Soft Computing Support Vector Machines, Neural Networks, and Fuzzy Logic Models”, the MIT Press 2001 � [2] L. Bottou et al. “Comparison of classifier methods: a case study in handwritten digit” recognition. Proceedings of the 12 th, IAPR International Conference on Pattern Recognition, vol. 2, � [3] Martin Law “A simple introduction to support vector machines”, Lecture for CSE 802 (note de cours), Department of Computer Science and Engineering, Michigan State University 2011 � [4] History of Support Vector Machines [en ligne]. <http: //www. svms. org/history. html> (9/11/2012) � [5] Colin Campbell, Yiming Ying “Learning with Support Vector Machines, SYNTHESIS LECTURES ON ARTIFICIAL INTELLIGENCE AND MACHINE LEARNING #10”, Morgan & Claypool publishers 2011 � [6] Bernhard Scholkopf, Alexander J. Smola “Learning with Kernels, Support Vector Machines, Regularization, Optimization, and Beyond”, the MIT Press 2002