Unidad N 1 Ecuaciones y Sistemas de Ecuaciones

Unidad N° 1 Ecuaciones y Sistemas de Ecuaciones Lineales ALGA- PROF. VILLAGRA – UNSa Sede Orán

Ecuación • Una ecuación es una función proposicional donde, al reemplazar sus variables por números se transforma en una proposición que puede ser verdadera o falsa. • Es un enunciado de la forma A= B donde A y B son expresiones algebraicas en x 1, x 2, x 3, …, xn. Donde x 1, x 2, x 3, …, xn. se denominan variables, también incógnitas o indeterminadas. Si a cada variable se la sustituye por un número determinado, el enunciado resultante puede ser Verdadero o Falso. Si el enunciado resulta verdadero, dichos números serán solución de la ecuación. • La solución de una ecuación en n variables, es el subconjunto CS de un conjunto universal U, cuyos elementos verifican la ecuación dada. • CS se denomina conjunto solución y es el conjunto cuyos elementos hacen verdadera la proposición abierta que define la ecuación dada. ALGA- PROF. VILLAGRA

Ejemplo • Por ejemplo • 3 x+2 y –z = x-1 es una ecuación con 3 incógnitas. • (1, 1, 5) es una solución de la ecuación ya que hace verdadera la misma, por lo tanto será elemento del conjunto solución, si hubiera otra terna que verifique la ecuación también pertenecerá al conjunto solución. • x 2 +9 = 6 x es una ecuación en una variable. 3 es la única solución de la ecuación, por lo tanto Cs = { 3} ALGA- PROF. VILLAGRA

Ecuaciones paramétricas: discusión, interpretación y representación. • Si en una ecuación de dos variables, ambas variables x e y se expresan separadamente en términos de una nueva variable t , de manera que la relación original entre x e y aun se mantenga, entonces, a la nueva variable t se le llama parámetro y las ecuaciones que definen la relación de las variable x y y con t se llaman representaciones paramétricas de la ecuación. • Una curva plana es un conjunto C de pares ordenados donde x e y son funciones de una variable t definidas en un intervalo I ALGA- PROF. VILLAGRA

• Sea C la curva determinada por todos los pares ordenados (x(t), y(t)), donde x e y están definidas en un intervalo I. Las ecuaciones : x= x(t), y= y(t) para , son las ecuaciones paramétricas de la curva C con parámetro t. La curva C se denomina curva parametrizada. • A partir de las ecuaciones paramétricas, eliminando el parámetro t, se obtiene la ecuación cartesiana de la Curva C, o sea una ecuación conocida en x e y para dicha curva. • Sean x: R→R e y: R→R, entonces son las ecuaciones paramétricas de la Curva C. ALGA- PROF. VILLAGRA

ALGA- PROF. VILLAGRA

ALGA- PROF. VILLAGRA

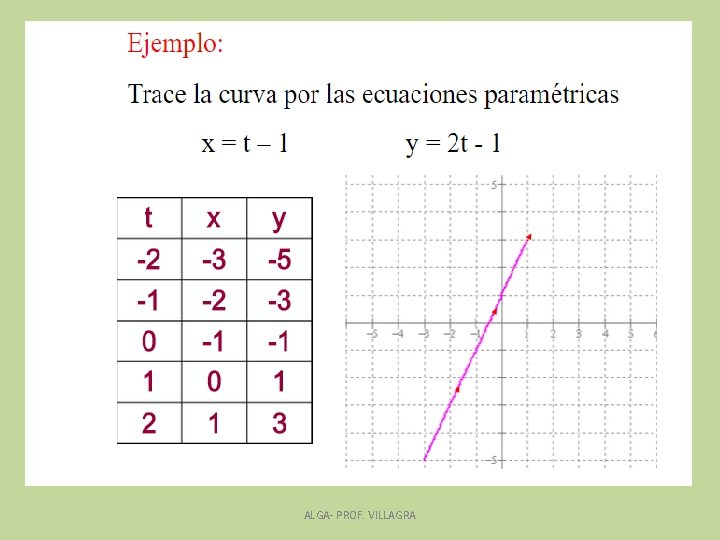
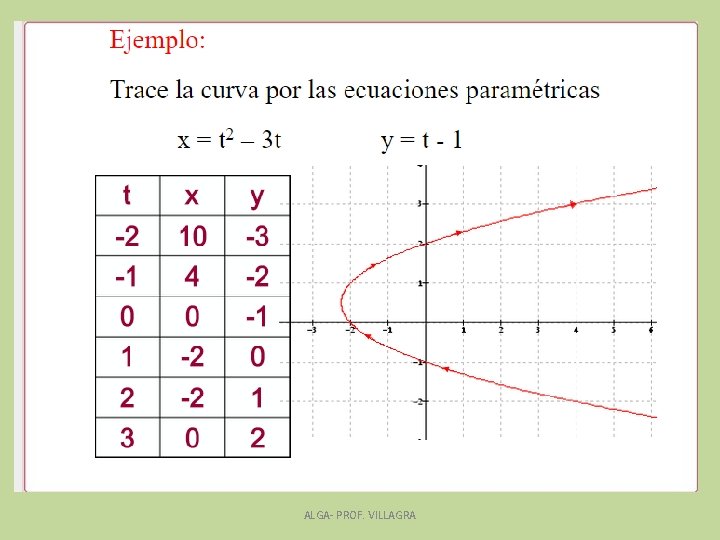
Ejemplo Considere las ecuaciones: Completemos la tabla. t -3 -2 -1 0 1 2 x y • Marque los puntos ( x, y) generados en la tabla, esbozar una grafica. Indicar la orientación. • Halle la ecuación rectangular o cartesiana eliminando el parámetro. Graficar. Comparar con la anterior. ALGA- PROF. VILLAGRA

Ecuación lineal • Una ecuación lineal sobre el cuerpo de los reales( R) con n incógnitas es una expresión de la forma Donde los Los se denominan coeficientes de las incógnitas y b se llama término constante. Se asume que los son valores conocidos ALGA- PROF. VILLAGRA

Solución de una ecuación lineal • Se dice que la n-upla es solución de la ecuación Si la proposición es verdadera Ejemplos: En la ecuación 3 x-y+4 z-w=6 La 4 -upla=(-5, 3, 6, 0) es una solución de la ecuación porque cuando se reemplaza por la incógnita correspondiente, la proposición es V. ALGA- PROF. VILLAGRA

• Para obtener las soluciones de una ecuación lineal con n incógnitas vamos a considerar tres casos: • 1)Uno de los coeficientes de los xi no es nulo. Es decir ai≠ 0 para algún i=1, 2, …, n • Supongamos que a 1≠ 0 • Al asignar valores a obtenemos un valor para en este caso. La ecuación tiene infinitas soluciones ALGA- PROF. VILLAGRA

• 2) Todos los coeficientes en la ecuación son nulos y la constante b no es nula. • Es decir que ai=0 para todo i: 1, 2, …n y b≠ 0 • Esto implica que si reemplazamos la ecuación por una n-upla será siempre falsa. • Es decir que la ecuación no tiene solución ya que no existe n-upla que satisfaga la ecuación ALGA- PROF. VILLAGRA

• 3) Todos los coeficientes de la ecuación son nulos y la constante b también es nula. Entonces es siempre verdadera. Es decir que cualquier n-upla de escalares en R es una solución de la ecuación. Ecuaciones equivalentes Dadas dos o más ecuaciones, estas son equivalentes si tienen el mismo conjunto solución. ALGA- PROF. VILLAGRA

Sistema de ecuaciones Lineales • Un sistema con m ecuaciones lineales con n incógnitas tiene la forma. • Donde los • Los aij son los coeficientes de los xj y los bi son las constantes de cada ecuación. ALGA- PROF. VILLAGRA

Solución sistema de ecuaciones lineales • Se dice que la n-upla de números reales es una solución ( o también una solución particular del sistema si satisface cada una de las ecuaciones. Es decir al reemplazar los xj por ki, i = 1, 2, …, n en cada ecuación, se verifica la igualdad. • El conjunto de todas las soluciones se llama conjunto solución o Solución General del sistema de ecuaciones lineales (SEL) ALGA- PROF. VILLAGRA

ALGA- PROF. VILLAGRA

Sistemas de ecuaciones lineales Equivalentes Se dice que dos sistemas de ecuaciones lineales son equivalentes si tienen el mismo conjunto solución. Esto es, cada solución del primer sistema es solución del segundo sistema y cada solución del 2 do sistema es una solución del primero. ALGA- PROF. VILLAGRA

Sistema de ecuaciones lineales homogeneo • Asociado al sistema de ecuaciones lineales que vimos anteriormente tenemos un sistema de ecuaciones donde las constantes son iguales a cero y se llama sistema homogéneo asociado. ALGA- PROF. VILLAGRA

Solución del sistema lineal homogéneo Siempre tiene solución ya que la n-upla (0, 0, …, 0) siempre será una solución, es decir verifica cada una de las ecuaciones. A esta solución se la denomina solución trivial o solución cero. Cualquier otra solución si existe, se llama solución distinta de cero o no trivial. En definitiva el sistema lineal homogéneo siempre tiene solución. Esas soluciones pueden única o infinitas soluciones. ALGA- PROF. VILLAGRA

ALGA- PROF. VILLAGRA

Metodo de Gauss Las operaciones que se llevan a cabo para obtener un sistema equivalente se llaman operaciones elementales. Existen tres tipos de operaciones elementales: 1) Intercambio de ecuaciones del S. E. L. 2) Reemplazar una ecuación del S. E. L. por un múltiplo escalar de ésta (se multiplica a ambos miembros de la ecuación por un escalar ≠ 0). 3) Reemplazar una ecuación del SEL por la suma de un múltiplo escalar de esta y un múltiplo escalar de otra ecuación del SEL. ALGA- PROF. VILLAGRA

Método de Gauss: utilización operaciones elementales 1) Si es necesario intercambiamos las ecuaciones de tal manera que la primera incógnita tenga un coeficiente no nulo en la primera ecuación, es decir 2) Para i>1 aplicamos la operación que reemplaza Ei por E’i = aii. Ei-ai 1 E 1 De esta manera eliminamos mínimamente la variable de las ecuaciones restantes y obtenemos el siguiente sistema de ecuaciones equivalente: ALGA- PROF. VILLAGRA

Donde es el 1 er coeficiente ≠ 0 de la segunda ecuación y acompaña a la variable Si durante este procedimiento que consiste en eliminar el primer coeficiente de E 2, Ej, … Em nos encontramos con: ALGA- PROF. VILLAGRA

El sistema es inconsistente y no tiene solución. Se elimina esta ecuación del sistema equivalente. Continuamos con el procedimiento desde la 2 da ecuación en adelante con cada subsistema, si no hay inconsistencia se reduce hasta la siguiente forma: ALGA- PROF. VILLAGRA

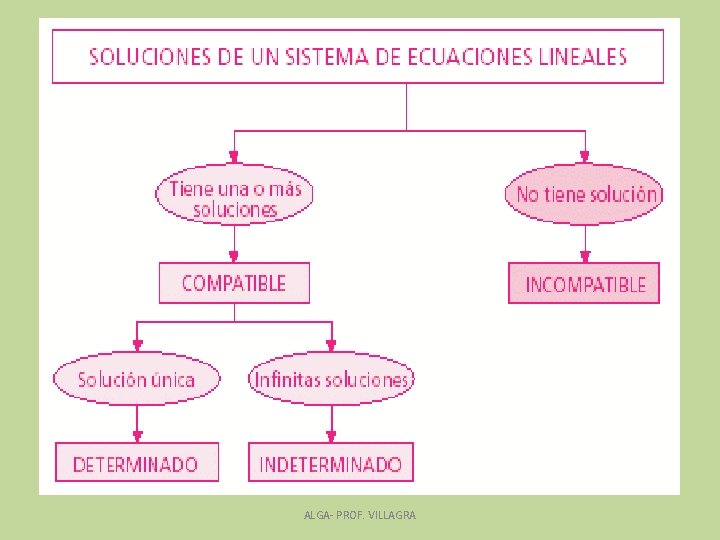
• r será el número de ecuaciones del sistema equivalente y n es el nro de incógnitas • Si r = n: igual numero de incógnitas que de ecuaciones, el SEL tiene solución única ( compatible determinado) • Si r<n: Número de ecuaciones es menor que el número de incógnitas, existen n-r variables libres y el SEL tiene más de una solución y se plantea una solución general en función de las variables libres. ( compatible indeterminado) ALGA- PROF. VILLAGRA

Método de Gauss Jordan • Es una variante del método de Gauss. • Lo que lo diferencia del método Gaussiano es que cuando es eliminada una incógnita, se eliminará de todas las ecuaciones restantes, o sea, las que anteceden a la ecuación principal así como de las que la siguen a continuación. • No es necesario entonces utilizar la sustitución hacia atrás para conseguir la solución. ALGA- PROF. VILLAGRA

Método de Gauss-Jordan ALGA- PROF. VILLAGRA