Unidad 2 ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR ECUACIONES

Unidad 2: ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR ECUACIONES LINEALES NO HOMOGÉNEAS (MÉTODO DE VARIACIÓN DE PARÁMETROS)

Introducción Para adaptar el método de variación de parámetros a una ecuación diferencial de segundo orden: primeramente se debe escribir la ecuación en la forma estándar ¢ Esta última ecuación es la análoga de segundo orden de la forma estándar de una ecuación lineal de primer orden ¢

Suposiciones Al resolver una EDLNH de primer orden, se supuso que yp=u(x)y 1(x). ¢ Supondremos ahora que la forma de la solución para la ecuación de orden 2 es yp=u 1(x)y 1(x)+u 2(x)y 2(x). Al utilizar la regla del producto para diferenciar dos veces yp se obtiene: ¢ yp´= u 1 y 1´+y 1 u 1´+u 2 y 2´+y 2 u 2´ yp´´= u 1 y 1´´+y 1´u 1´+y 1 u 1´´+u 1´y 1´+u 2 y 2´´+y 2´u 2´+y 2 u 2´´+ u 2´y 2´

Suposiciones… Al sustituir yp=u 1(x)y 1(x)+u 2(x)y 2(x) y sus derivadas en la ecuación tenemos: De donde:

Suposiciones… Como se busca determinar dos funciones desconocidas u 1 y u 2, es necesario tener dos ecuaciones. ¢ Estas dos ecuaciones se obtienen con la suposición adicional de que u 1 y u 2 satisfacen: Con ello la ecuación Se reduce a:

Suposiciones… ¢ Ahora se cuenta con las dos ecuaciones deseadas Por la regla de Cramer la solución del sistema de ecuaciones puede expresarse en términos de determinantes:

Suposiciones… Finalmente se encuentran u 1 y u 2 integrando los resultados anteriores. ¢ Con ello: ¢

Resumen del método ¢ Para resolver la EDLNH en forma estándar: y´´ + P(X)y´ + Q(x)y = f(x) Se resuelve la EDLH asociada de la EDLNH original, para determinar la solución homogénea yh=c 1 y 1(x)+c 2 y 2(x). l Se supone que la solución particular de la EDLNH se puede obtener a partir de la solución de la EDLH variando los parámetros, esto es: suponiendo que yp=u 1(x)y 1(x)+u 2(x)y 2(x). l

Resumen del método… l Sustituyendo esta última ecuación en la EDLNH original, con el propósito de obtener las funciones desconocidas u 1(x) y u 2(x), obtenemos después de arreglar términos, el sistema de dos ecuaciones con dos incógnitas l Resolviendo este sistema de ecuaciones simultaneas por la Regla de Cramer

Resumen del método… l Integramos estas dos ecuaciones para obtener u 1(x) y u 2(x). Sustituimos estas dos funciones en la solución propuesta yp=u 1(x)y 1(x)+u 2(x)y 2(x). l Sumamos las dos soluciones, así: y=yh+yp. l

Ejemplo ¢ Resuelva 4 y´´+36 y=Csc(3 x) La forma estándar de la EDLNH es: y´´-9 y=(1/4)Csc(3 x) l La ecuación auxiliar m 2+9 tiene raíces conjunadas m 1=3 i y m 2=-3 i, por ello: yh=c 1 Cos(3 x)+c 2 Sen(3 x). l Con y 1=Cos(3 x), y 2=Sen(3 x) y f(x)=(1/4) Csc(3 x) se obtiene: l

Ejemplo… l A partir de esto:

Ejemplo… l Integrando: l Con esto: l Y finalmente, como:

Generalización del método ¢ Para resolver la EDLNH en forma estándar: y(n)+Pn-1(X)y(n-1)+ P 1(x)y´+P 0(x)y= f(x) Se resuelve la EDLH asociada de la EDLNH original, para determinar la solución homogénea yh=c 1 y 1(x)+c 2 y 2(x)+ …+ cnyn(x) l Se supone que la solución particular de la EDLNH se puede obtener a partir de la solución de la EDLH variando los parámetros, esto es: suponiendo que yp=u 1(x)y 1(x)+u 2(x)y 2(x)+ … +un(x)yn(x) l

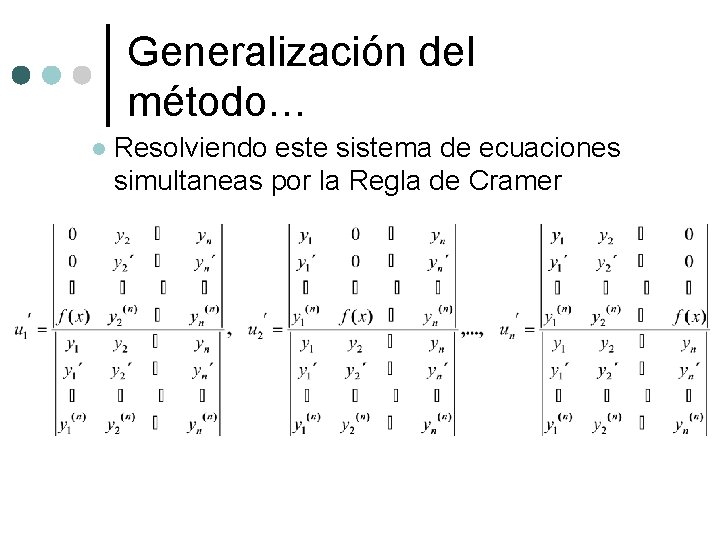
Generalización del método… l Sustituyendo esta última ecuación en la EDLNH original, con el propósito de obtener las funciones desconocidas u 1(x) y u 2(x), . . . un(x), , obtenemos después de arreglar términos, el sistema de n ecuaciones con n incógnitas

Generalización del método… l Resolviendo este sistema de ecuaciones simultaneas por la Regla de Cramer

Generalización del método… Integramos estas las ecuaciones para obtener u 1(x) y u 2(x), …, un(x). l Sustituimos estas n funciones en la solución propuesta yp=u 1(x)y 1(x)+u 2(x)y 2(x)+ un(x)yn(x). l Sumamos las dos soluciones, así: y=yh+yp. l

Problemas ¢ Resuelva las siguientes ecuaciones diferenciales: