Unidad 1 ECUACIONES DIFERENCIALES DE PRIMER ORDEN MTODOS

Unidad 1: ECUACIONES DIFERENCIALES DE PRIMER ORDEN MÉTODOS NUMÉRICOS

Curvas solución sin una solución (Campo de dirección) ¢ Si se evalúa f de forma sistemática en una red de puntos rectangular en el plano xy y se traza un elemento lineal en cada punto (x, y) de la red con pendiente f(x, y), entonces la colección de estos elementos lineales se llama campo de dirección o campo de pendientes de la ecuación diferencial dy/dx=f(x, y).

Campo de dirección ¢ De manera gráfica, un campo de dirección indica la apariencia o forma de una familia de curvas solución de la ecuación diferencial y, en consecuencia, podría ser posible ver de un vistazo ciertos aspectos cualitativos de las soluciones.

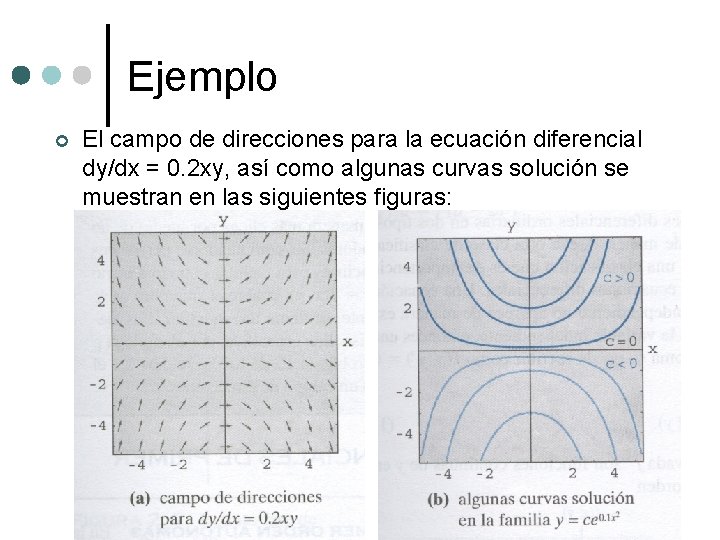
Ejemplo ¢ El campo de direcciones para la ecuación diferencial dy/dx = 0. 2 xy, así como algunas curvas solución se muestran en las siguientes figuras:

Solución del PVI ¢ Suponga que el Problema de Valor Inicial de primer orden: y´=f(x, y) con y(x 0)=y 0 posee una solución. ¢ Una forma de poder aproximar esta solución es utilizar rectas tangentes.

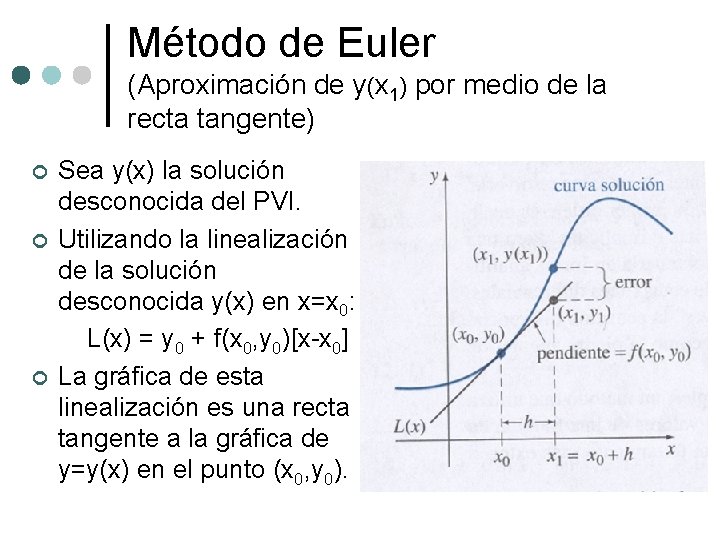
Método de Euler (Aproximación de y(x 1) por medio de la recta tangente) ¢ ¢ ¢ Sea y(x) la solución desconocida del PVI. Utilizando la linealización de la solución desconocida y(x) en x=x 0: L(x) = y 0 + f(x 0, y 0)[x-x 0] La gráfica de esta linealización es una recta tangente a la gráfica de y=y(x) en el punto (x 0, y 0).

Método de Euler. . . Si representamos con h un incremento positivo en el eje x, entonces al sustituir x por x 1=x 0+h se obtiene: L(x 1) = y 0 + f(x 0, y 0)(x 0+h-x 0) ó y 1 = y 0 + hf(x 1, y 1) donde: y 1 = L(x 1) ¢ El punto (x 1, y 1) en la recta tangente es una aproximación al punto (x 1, y(x 1)) en la solución. La precisión de la aproximación depende del tamaño de h. ¢

Método de Euler. . . ¢ ¢ ¢ Por lo común, se debe elegir este tamaño de paso como “razonablemente pequeño”. Si repetimos el proceso para una segunda recta tangente en (x 1, y 1) tenemos ahora: y(x 2) = y(x 0+2 h) = y(x 1+h) Lo anterior es aproximadamente igual a y 2 = y 1+hf(x 1, y 1) Continuando de esta manera se puede obtener una forma recursiva: yn+1 = yn + hf(xn, yn) donde xn=x 0+nh para n=0, 1, 2, … Este procedimiento se conoce como método de Euler.

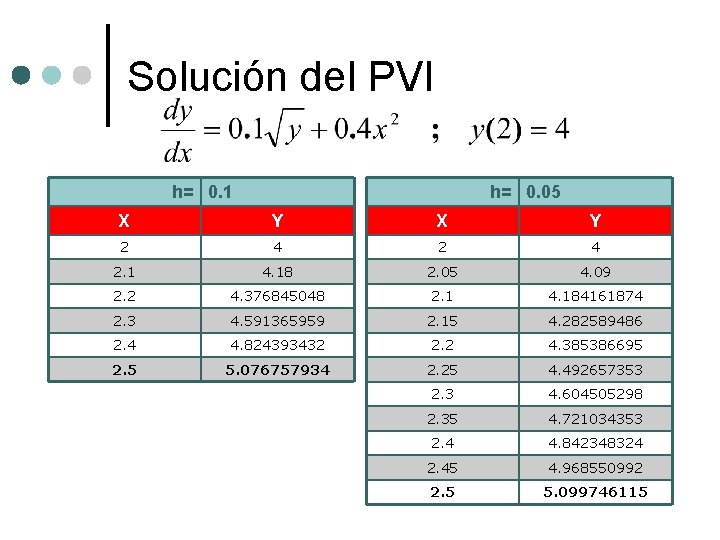
Problema ¢ Considere el problema de valor inicial: Use el Método de Euler para obtener una aproximación de y(2. 5) primero con h=0. 1 y luego con h=0. 05

Solución del PVI h= 0. 1 h= 0. 05 X Y 2 4 2. 1 4. 18 2. 05 4. 09 2. 2 4. 376845048 2. 1 4. 184161874 2. 3 4. 591365959 2. 15 4. 282589486 2. 4 4. 824393432 2. 2 4. 385386695 2. 5 5. 076757934 2. 25 4. 492657353 2. 3 4. 604505298 2. 35 4. 721034353 2. 4 4. 842348324 2. 45 4. 968550992 2. 5 5. 099746115

Problemas ¢ Utilice el Método de Euler para obtener una aproximación de al menos cuatro cifras del valor indicado. y(0)=1 y(0. 5) h=0. 05 y(1)=1 y(1. 5) h=0. 01 y(0)=1 y(p/2) h=0. 1