Unidad 3 Medidas de Posicin y Centralizacin Estadstica

Unidad 3 Medidas de Posición y Centralización Estadística E. S. O.

Objetivos ◊ De las diferentes medidas descriptivas de una distribución de frecuencias, que se presentan a lo largo del tema, el alumno deberá comprender el interés y el objetivo de cada una de ellas; así mismo sabrá aplicar su definición y manejar sus principales propiedades ◊ Todas ellas comparten el propósito común de servir de indicadores de la Posición (Central y No Central) que ocupan un conjunto de datos. De esta forma, con su uso se aprenderá a “sintetizar o resumir” la información contenida en un conjunto de datos indicando su POSICIÓN global ◊ Interpretar correctamente los valores obtenidos para estas medidas ◊ Diferenciar y elegir aquella medida - de entre las alternativas presentadas que resulte más conveniente para describir los aspectos que se pretenden poner de manifiesto.

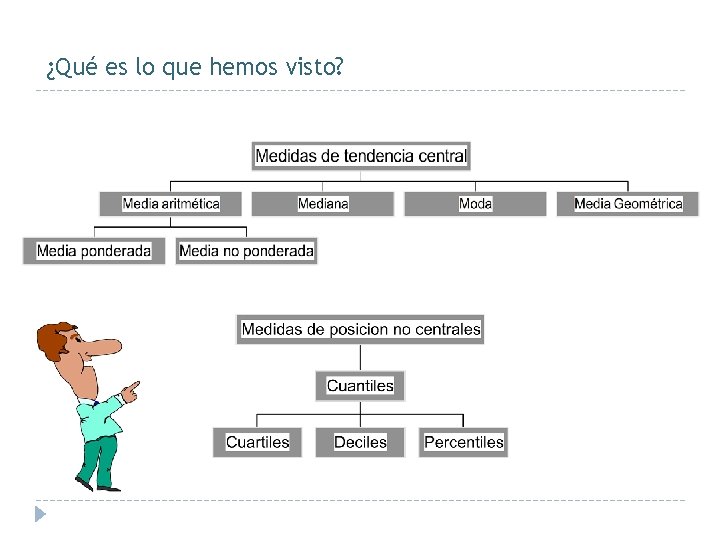
Índice 1. - Introducción 2. - Medidas de Posición 2. 1 - Medidas de tendencia central Media aritmética, geométrica y ponderada, Mediana y Moda 2. 2. - Medidas no centrales Cuantiles: Cuartiles, deciles, percentiles

1 Introducción Un objeto pequeño se pesa con un mismo instrumento por ocho estudiantes de una clase, obteniéndose los siguientes valores en gramos: 6´ 2, 6´ 0, 6´ 3, 6´ 1, 6´ 23, 6´ 15, 6´ 2 ¿Cuál sería la mejor estimación del peso real? ¿Cómo determinar, a partir de un conjunto de medidas x 1, x 2 , . . . , xn la mejor estimación posible del verdadero valor X desconocido?

1 Introducción ¿Cuál sería la mejor estimación del peso real? No tenemos ninguna razón para pensar que el verdadero valor esté más cercano a uno u otro de los datos obtenidos. ¿ 6´ 1475? (6´ 2 + 6´ 0 + 6´ 3 + 6´ 1 + 6´ 23 + 6´ 15 + 6´ 2) / 8 ¿ 6´ 0 , 6´ 2? Valores que más se repiten ¿ 6´ 15 – 6´ 2? 6´ 0, 6´ 1, 6´ 15, 6´ 2, 6´ 23, 6´ 3

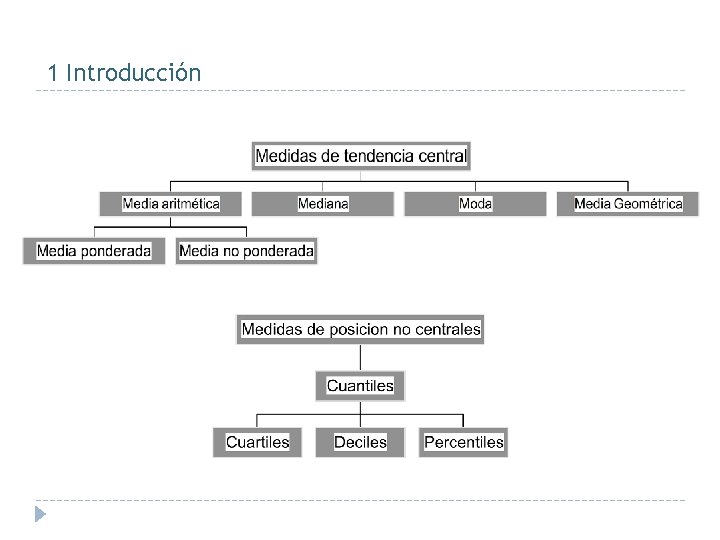
1 Introducción ◊ Las Medidas de Posición van a desvelar aquellos valores con respecto de los cuales, los datos suelen disponerse. ◊ Son magnitudes que pueden considerarse como “representativas” del grueso de los datos, sirviendo de referencia a los mismos ◊ Se clasifican en: ◊ Medidas de centralización ◊ Medidas de posición no centrales Unidad 2: Medidas de Posición

1 Introducción

Recordar… Distribución de Frecuencias

2. 1. 1. - Medida Aritmética Definición En un conjunto de datos agrupados: {(xi , ni); i=1, . . . , k} N = n 1 + n 2 +. . . + nk: el número de datos observados Se define la Media Aritmética por

2. 1. 1. - Medida Aritmética Cálculo Variables cuantitativas discretas o no agrupadas Variables cuantitativas continuas o agrupadas xi serán marcas de clase Variables cualitativas no tiene sentido

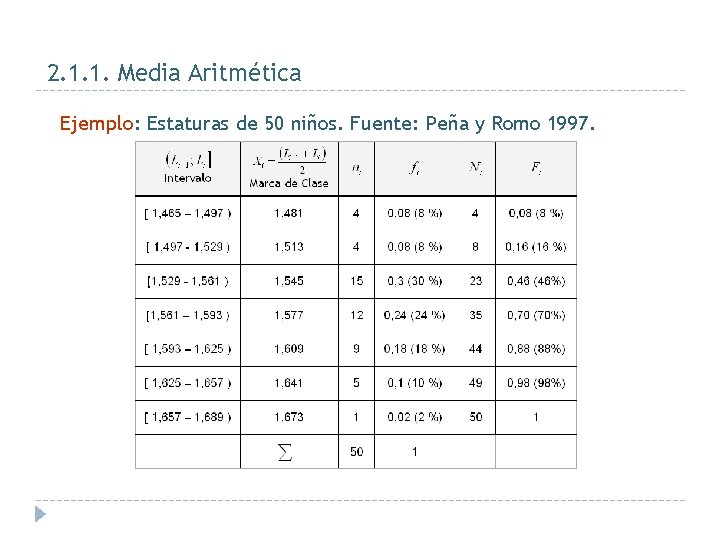
2. 1. 1. Media Aritmética Ejemplo: Estaturas de 50 niños. Fuente: Peña y Romo 1997.

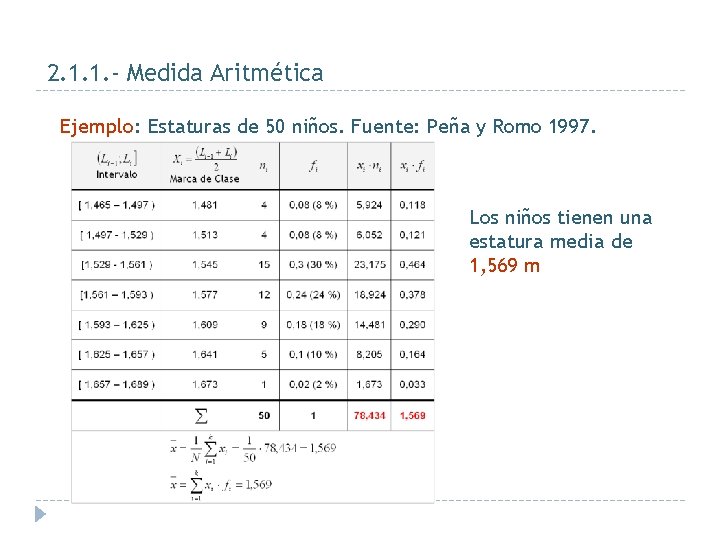
2. 1. 1. - Medida Aritmética Ejemplo: Estaturas de 50 niños. Fuente: Peña y Romo 1997. Los niños tienen una estatura media de 1, 569 m

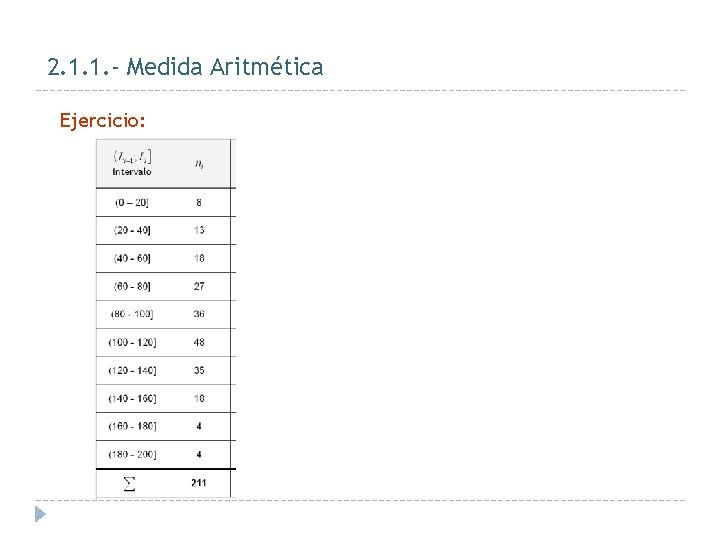
2. 1. 1. - Medida Aritmética Ejercicio:

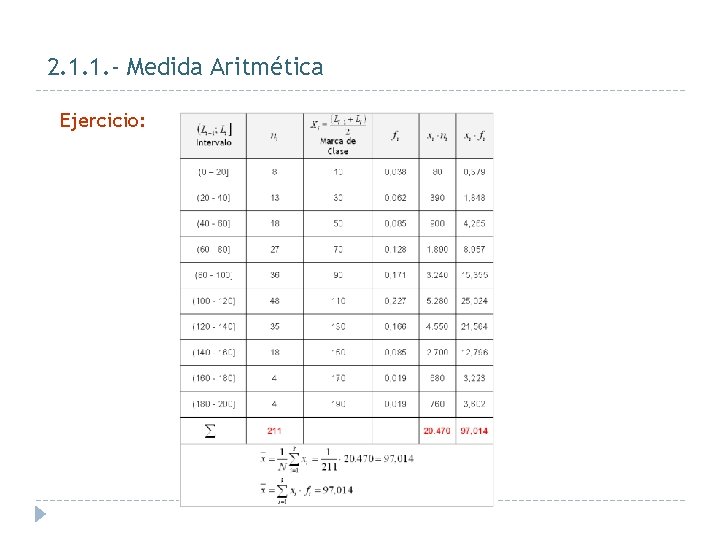
2. 1. 1. - Medida Aritmética Ejercicio:

2. 1. 2. - Medida Aritmética Ponderada Media aritmética en la que se tiene en cuenta la importancia específica de cada uno de sus datos, a través de unos pesos, dando así a éstos mayor o menor relevancia o aportación al cálculo de la media. Ejemplo: Las notas obtenidas por un estudiante en cada parte de una determinada materia, así como los pesos de importancia de las distintas unidades, son los que se presentan en la tabla.

2. 1. 2. - Medida Aritmética Ponderada Definición En un conjunto de datos agrupados: {(xi , ni); i=1, . . . , k} N = n 1 + n 2 +. . . + nk: el número de datos observados Sean {wi; i=1, . . . , k} un conjunto de pesos que ponderan la importancia de cada uno de los datos observados, verificando que: wi 0 para i =1, . . . , k Se define la Media Aritmética Ponderada por

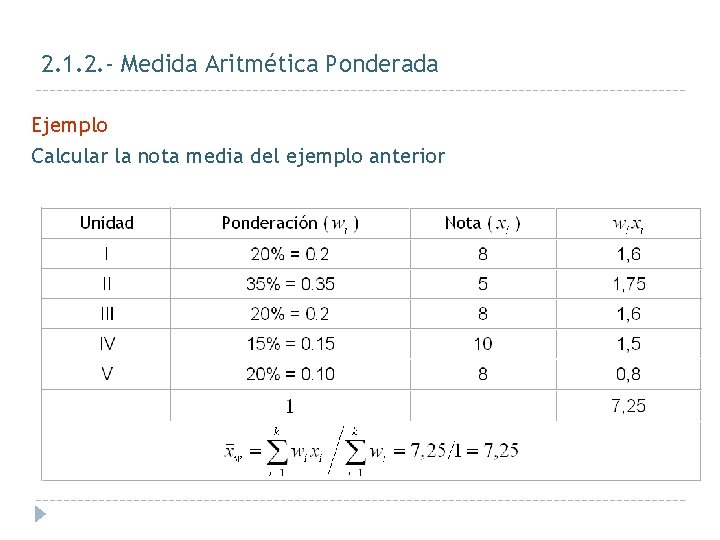
2. 1. 2. - Medida Aritmética Ponderada Ejemplo Calcular la nota media del ejemplo anterior

2. 1. 3. - Medida Geométrica Definición: Sea X una variable cuantitativa medida en una escala de razón y que sólo toma valores positivos. En la distribución de frecuencias: {(xi , ni); i=1, . . . , k} Se define la Media Geométrica – la denotamos G - como: Es útil para promediar tasas, porcentajes, tipos de interés y, en general, en todas aquellas situaciones en las que la variable analizada presente variaciones acumulativas

2. 1. 4 Mediana Definición La Mediana (Me) es aquél valor o dato de la distribución, que divide a ésta en dos partes iguales dejando al 50% de las frecuencias por debajo y al 50% por encima. Ejemplo: valores observados de una variable : 2, 3, 3, 3, 5, 6, 6, 7 y 9 La mediana es 5, pues es el valor que deja el mismo número de datos (4) por debajo que por encima de él. Para su cálculo distinguiremos según tengamos distribuciones: ü Discretas ü Continuas o agrupadas

2. 1. 4 Mediana Distribuciones discretas Pasos a seguir en su cálculo: Ordenamos de forma creciente los datos: Si m < N/2 m+1 con m entero Me = x(m+1) Ejercicio: 2, 3, 3, 3, 5, 6, 6, 7 y 9 N / 2 = 4, 5 4 < 4, 5 < 5 Me = x(m+1) = x 5 =5

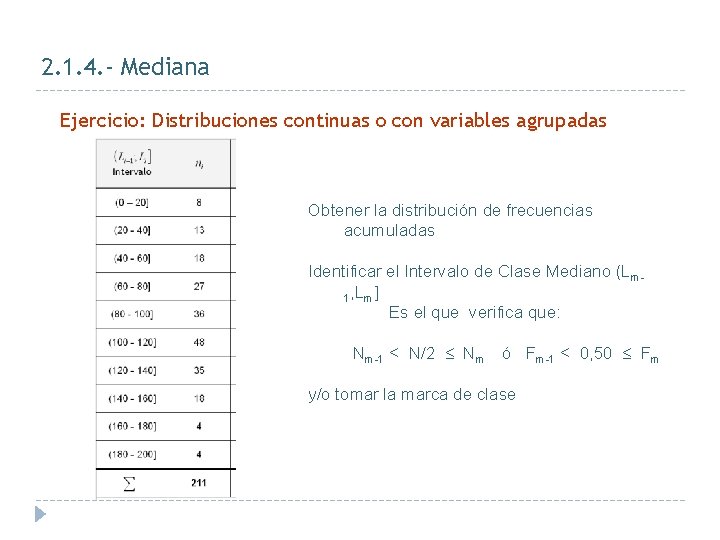
2. 1. 4. - Mediana Ejercicio: Distribuciones continuas o con variables agrupadas Obtener la distribución de frecuencias acumuladas Identificar el Intervalo de Clase Mediano (Lm 1, Lm] Es el que verifica que: Nm-1 < N/2 Nm ó Fm-1 < 0, 50 Fm y/o tomar la marca de clase

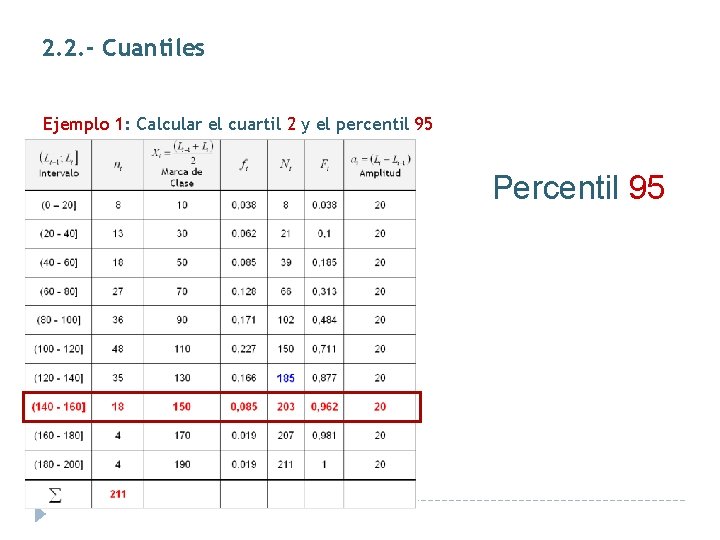
2. 1. 4. - Mediana Identificar el Intervalo de Clase Mediano (Lm-1, Lm] Es el que verifica que: 102 = Nm-1 < 105, 2 = N/2 Nm = 150 ó 0, 484 = Fm-1 < 0, 50 Fm = 0, 711 (100 – 120] o marca de clase = 110

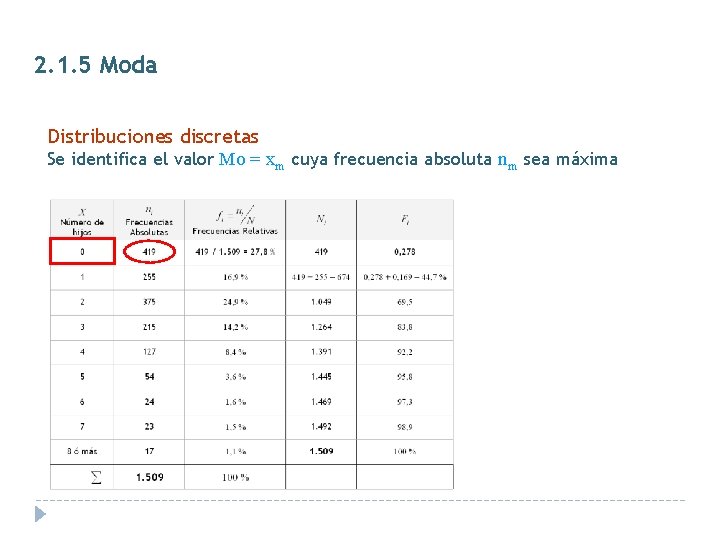
2. 1. 5 Moda Definición La Moda (Mo) de una distribución de frecuencias es el valor más frecuente de la misma. Dependiendo del número de modas, las distribuciones se clasifican en Unimodales, Bimodales o Multimodales. Ejemplo: valores observados de una variable : 2, 3, 3, 3, 5, 6, 6, 7 y 9 La moda es 3, pues es el valor más frecuente. Para su cálculo distinguiremos según tengamos distribuciones: ü Discretas ü Continuas o agrupadas

2. 1. 5 Moda Distribuciones discretas Se identifica el valor Mo = xm cuya frecuencia absoluta nm sea máxima

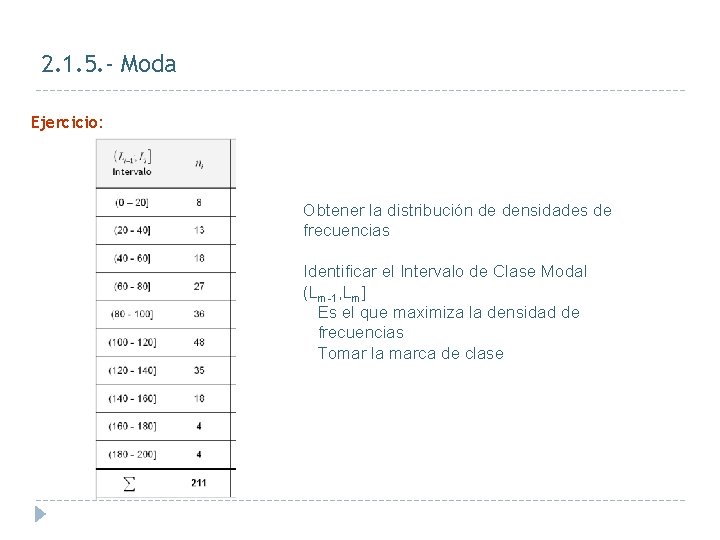
2. 1. 5 Moda Distribuciones continuas o agrupadas Como los valores de la variable están incluidos en intervalos de clase no es posible identificar directamente el valor o valores centrales. Pasos a seguir en su cálculo: 1. Obtener la densidad de frecuencia (dm=nm/am) 2. Identificar el Intervalo de Clase Modal (Lm-1, Lm] Es el que maximiza dm y/o tomar la marca de clase

2. 1. 5. - Moda Ejercicio: Obtener la distribución de densidades de frecuencias Identificar el Intervalo de Clase Modal (Lm-1, Lm] Es el que maximiza la densidad de frecuencias Tomar la marca de clase

2. 1. 5. - Moda Identificar el Intervalo de Clase Modal (Lm-1, Lm] Es el que verifica que maximiza di = 2, 4 (100 – 120] o marca de clase =110

2. 2. Cuantiles Son aquellos valores de la variable, que ordenados de menor a mayor, dividen a la distribución en partes, de tal manera que cada una de ellas contiene el mismo número de frecuencias. Los tipos más importantes de cuantiles son: ü ü ü Los cuartiles, que dividen a la distribución en cuatro partes Los deciles, que dividen a la distribución en diez partes Los percentiles, que dividen a la distribución en cien partes

2. 2. Cuantiles Definición Para 0 ≤ (p) ≤ 1 se define el Cuantil de orden (p) como el valor de la variable o dato tal que el x 100 de los datos son inferiores. Lo denotamos Q (Qp) Q 70 Casos particulares notables son los: Percentiles, Cuartiles y Deciles

2. 2. Cuantiles Distribuciones discretas Si m < N·p m+1 con m entero entonces Qp = x(m+1) Distribuciones Continuas o Agrupadas Su aproximación se basa en un argumento idéntico al utilizado en el cálculo de la Mediana para datos agrupados

2. 2. - Cuantiles Cuartiles: {Ci = Qi/4 i = 1, 2, 3} ü Primer Cuartil C 1 ≡ Cuantil 0. 25 (Q 0. 25) ü Segundo Cuartil C 2 ≡ Cuantil 0. 5 (Q 0. 5) ü Tercer Cuartil C 3 ≡ Cuantil 0. 75 (Q 0. 75) Deciles: {Di = Qi/10 i = 1, . . . , 9} Percentiles: {Pi = Qi/100 i = 1, . . . , 99} Ejemplo: En cualquier conjunto de datos: El percentil P 95 es superado únicamente por el 5% de los datos.

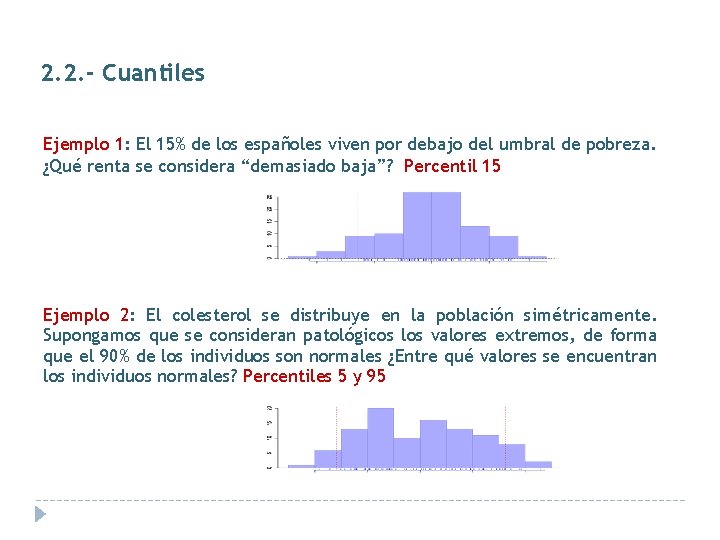
2. 2. - Cuantiles Ejemplo 1: El 15% de los españoles viven por debajo del umbral de pobreza. ¿Qué renta se considera “demasiado baja”? Percentil 15 Ejemplo 2: El colesterol se distribuye en la población simétricamente. Supongamos que se consideran patológicos los valores extremos, de forma que el 90% de los individuos son normales ¿Entre qué valores se encuentran los individuos normales? Percentiles 5 y 95

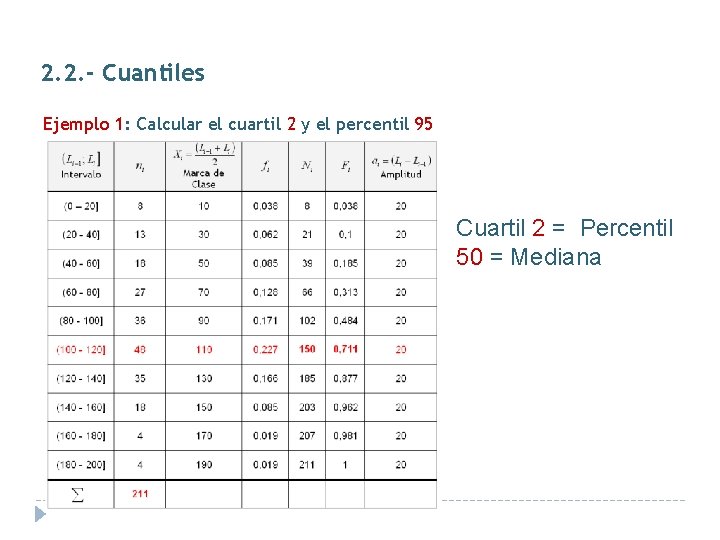
2. 2. - Cuantiles Ejemplo 1: Calcular el cuartil 2 y el percentil 95 Cuartil 2 = Percentil 50 = Mediana

2. 2. - Cuantiles Ejemplo 1: Calcular el cuartil 2 y el percentil 95 Percentil 95

¿Qué es lo que hemos visto?

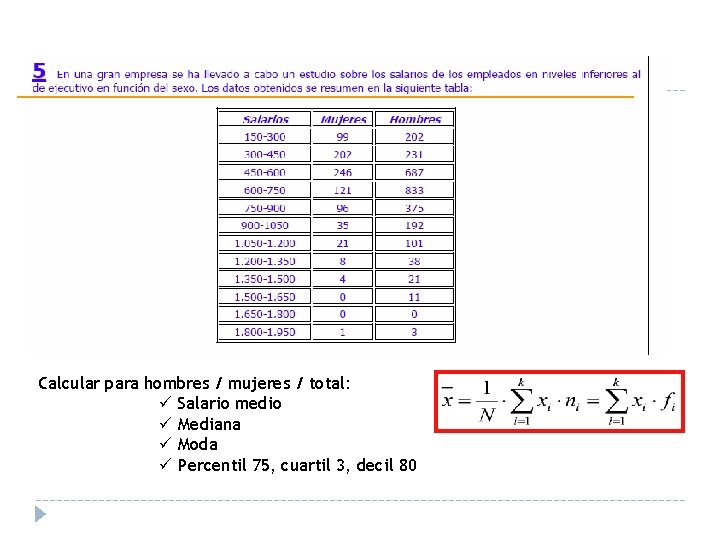
Calcular para hombres / mujeres / total: ü Salario medio ü Mediana ü Moda ü Percentil 75, cuartil 3, decil 80