MATEMTICA 6 ano MEDIDAS ENVOLVENDO GRANDEZAS MEDIDAS ENVOLVENDO

MATEMÁTICA 6º ano MEDIDAS ENVOLVENDO GRANDEZAS

MEDIDAS ENVOLVENDO GRANDEZAS As unidades de medida são representações das grandezas físicas utilizadas em diversas áreas do conhecimento com o objetivo de quantificar uma matéria, uma sensação, o tempo ou o tamanho de algo, por exemplo. Em todo o mundo as unidades de medida seguem um padrão determinado pelo : Sistema Internacional de Unidades (SI). A partir da unidade-padrão estabelecida pelo Sistema Internacional, podemos ainda utilizar outras unidades derivadas dela, o que permite compararmos e ampliarmos a noção quantitativa da grandeza. O Sistema Internacional adota a unidade kelvin, por exemplo, como padrão para a grandeza temperatura. Essa unidade é muito utilizada em experimentos laboratoriais, mas, no dia a dia, a maioria dos países utiliza a unidade graus Celsius.

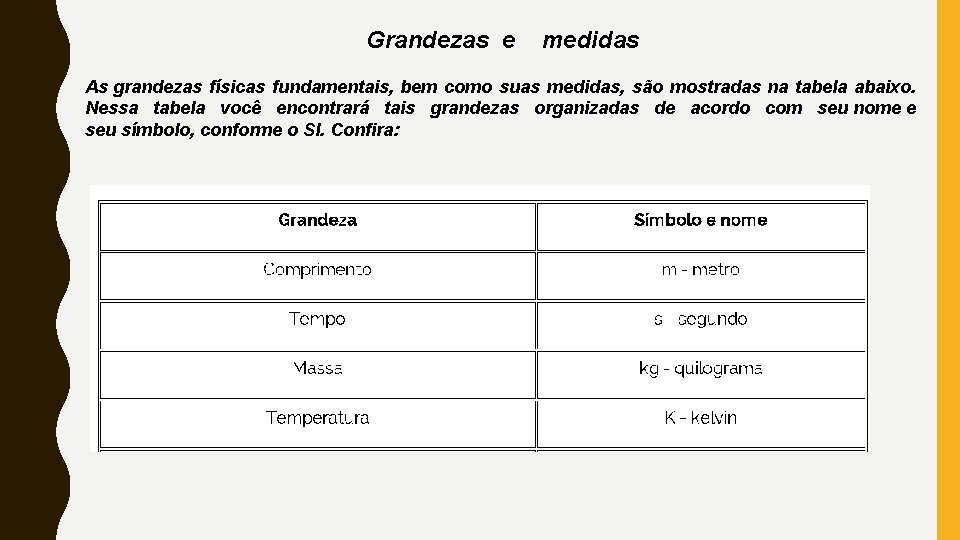
Grandezas e medidas As grandezas físicas fundamentais, bem como suas medidas, são mostradas na tabela abaixo. Nessa tabela você encontrará tais grandezas organizadas de acordo com seu nome e seu símbolo, conforme o SI. Confira:

� Temperatura A temperatura é uma grandeza física utilizada para medir o grau de agitação ou a energia cinética das moléculas de uma determinada quantidade de matéria. Quanto mais agitadas essas moléculas estiverem, maior será sua temperatura. O aparelho utilizado para fazer medidas de temperatura é o termômetro, que pode ser encontrado em três escalas: Celsius, Kelvin e Fahrenheit.

� Diferenças entre grandezas escalares e vetoriais Todas as grandezas físicas podem ser classificadas em dois tipos: as grandezas escalares e as vetoriais. A diferença mais básica entre esses dois tipos de grandezas é que as escalares podem ser representadas de forma satisfatória por intermédio apenas do número e de uma unidade de medida. Em contrapartida, as grandezas vetoriais precisam ser expressas com base em mais informações, como o seu valor numérico, direção e sentido, além de uma unidade de medida. � Grandezas escalares são aquelas que podem ser escritas na forma de um número, seguido de uma unidade de medida. Em outras palavras, elas são completamente definidas se soubermos o seu valor, também chamado de módulo, e a forma como ela é medida. São exemplos de grandezas escalares o comprimento, o tempo, a temperatura e a massa. Confira algumas formas como essas grandezas podem ser expressas: • 1 m – um metro; 10 cm – dez centímetros; 2 mm – dois milímetros. • 10 s – dez segundos; 15 min – quinze minutos; 1 h – uma hora. • 25º C – vinte e cinco graus Celsius; 86º F – oitenta e seis graus Fahrenheit; 10 K – dez kelvin. • 200 g – duzentos gramas; 10 mg – dez miligramas; 2 kg – dois quilogramas.

� Unidades de comprimento As unidades mais utilizadas para o trabalho comprimento são: • Quilômetro (km); • Metro (m) [unidade-padrão de comprimento segundo o SI: • Centímetro (cm); • Decímetro (dm); • Milímetro (mm). Para converter uma unidade na outra, basta seguir estas relações: • 1 km = 1000 m • 1 m = 100 cm • 1 dm = 10 cm • 1 cm = 10 mm Conversão de unidades de comprimento Exemplo 1: vamos transformar 5 km em dm. Analisando o esquema, a diferença entre km e dm é da ordem de 100000, assim, basta montar a seguinte regra de três:

Exemplo 2: vamos transformar 500 mm em cm. Como 1 cm equivale a 10 mm, basta utilizar a seguinte regra de três: � Unidades de tempo • Hora (h); • Minuto (min); • Segundo (s) [unidade]padrão de tempo estabelecida pelo SI]. Para converter uma unidade na outra, basta seguir estas relações: • 1 h = 60 min • 1 min = 60 s

Conversão de unidades de tempo Exemplo 1: vamos transformar 6 h em segundos. Como 1 hora equivale a 3600 segundos (resultado da multiplicação 60 x 60 da diferença entre horas e segundos), basta montar a seguinte regra de três: Exemplo 2: vamos transformar 600 s em minutos. Como 1 minuto equivale a 60 s, basta utilizar a seguinte regra de três:

Diferença entre massa e peso Massa e peso são grandezas diferentes. A massa mede a quantidade de matéria de um corpo, e o peso mostra a relação da massa com a aceleração da gravidade local. � A massa é “a quantidade de matéria presente em um corpo e medida em uma balança”. No Sistema Internacional de Unidades, a unidade padrão escolhida desde 1960 para a massa é o quilograma (kg). � Peso O peso, por sua vezm pode ser calculado por meio da multiplicação entre a massa do corpo e a aceleração da gravidade local: P = m. g OBS. : A unidade padrão do peso no SI é o Newton (1 N = 1 kg. m/s 2). O peso depende da atração que um corpo exerce sobre o outro, que é determinada pela aceleração da gravidade. Quanto maior for a massa do corpo, maior será essa atração. A massa da Terra (5, 97. 1024 kg) é bem maior que a massa da Lua (7, 4. 1022 kg), por isso, o corpo de uma pessoa é mais atraído pela superfície da Terra do que pela superfície da Lua. Em outras palavras, a aceleração da gravidade na Terra é maior, e isso afeta o peso do corpo atraído por ela.

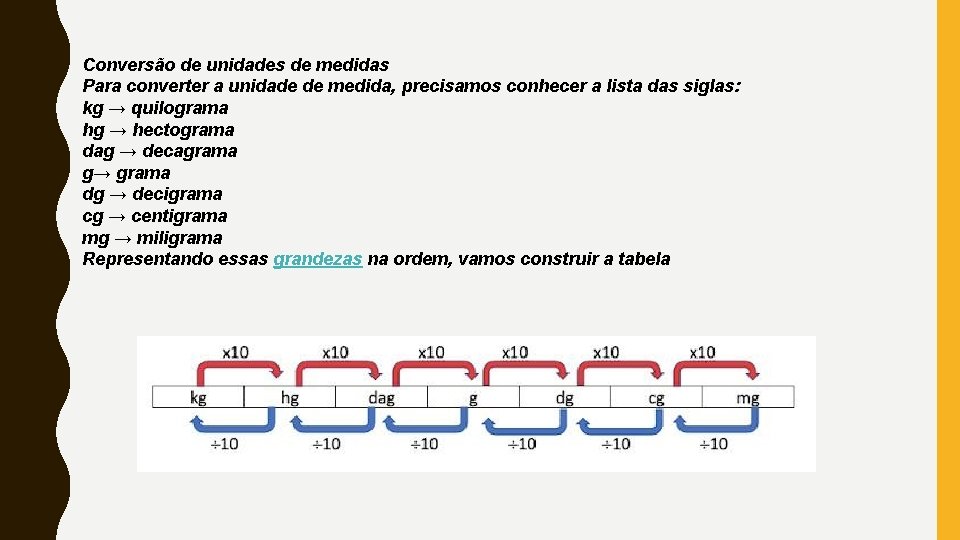
Conversão de unidades de medidas Para converter a unidade de medida, precisamos conhecer a lista das siglas: kg → quilograma hg → hectograma dag → decagrama g→ grama dg → decigrama cg → centigrama mg → miligrama Representando essas grandezas na ordem, vamos construir a tabela

A fim realizarmos a conversão de uma unidade que está à esquerda para outra que está à direita, multiplicamos por 10 cada unidade. • Exemplo Convertendo 15 g → mg Ao analisar-se a tabela, de grama até miligrama, tem-se três unidades de medida: g→ dg → cg → mg Multiplicaremos cada unidade por 10: 15 · 10 = 15 · 1000 = 15. 000 mg Para realizar conversões da direita para a esquerda, dividimos por 10 para cada unidade de medida. • Exemplo 2 Convertendo 12. 000 cg → hg Ao analisar-se a tabela, de centigrama para hectograma, tem-se quatro unidades de medida. hg ← dag ← dg ← cg Dividiremos cada unidade por 10: 12. 000 : 10 = 12. 000 : 10. 000 = 1, 2 hg

� Unidades de volume • Metro cúbico (m 3) [unidade-padrão de volume segundo o SI]; • Litro (L) ou decímetro cúbico (dm 3); • Mililitro (m. L) ou centímetro cúbico (cm 3). Para converter uma unidade na outra, basta seguir estas relações: • 1 m 3 = 1000 L • 1 L = 1 dm 3 • 1 L = 1000 m. L • 1 dm 3 = 1000 cm 3 • 1 cm 3 = 1 m. L Como podemos acompanhar no esquema acima, uma unidade de volume é sempre 1000 vezes maior que a outra. Quando comparamos a unidade maior (m 3) com a unidade menor (m. L ou cm 3), a diferença é de 1000000 de vezes. Conversão de unidades de volume Exemplo 1: vamos transformar 4, 5 m 3 em dm 3. Como 1 m 3 equivale a 1000 dm 3, podemos montar a seguinte regra de três:

Exemplo 2: vamos transformar 300 cm 3 em L. Como 1 L equivale a 1000 de cm 3, podemos montar a seguinte regra de três: MEDIDAS DE CAPACIDADE Grandezas que estimam a quantidade de líquido em um recipiente As medidas de capacidade são grandezas utilizadas para estimar uma quantidade que está inserida em um reservatório/recipiente, ou seja, são empregadas na medição de líquidos. Ainda pode-se dizer que tais medidas são usadas para definir o volume no interior de um recipiente.

Mas, antes de conhecer as unidades de medidas de capacidade é importante fazer a distinção entre alguns termos. Quando falarmos em volume, estamos nos referindo ao espaço que um corpo é capaz de ocupar. Mas ao falar de capacidade, estamos nos referindo ao volume de líquido que pode ser acomodado dentro do recipiente. As medidas de capacidade fazem parte do nosso cotidiano. Elas são utilizadas, por exemplo, quando queremos saber quantos litros de água estão dentro de um tanque ou, ainda, quantos litros de leite estão dentro da caixa. Perceba que geralmente o litro é utilizado como referência ao se falar em líquidos. Isso porque ele foi definido pelo Sistema Internacional de Unidades (SI) como a unidade padrão de medidas de capacidade. Contudo existem várias outras medidas, quer saber quais são? Acompanhe na explicação abaixo! Medidas de capacidade Em algumas situações, é necessário utilizar medidas de capacidades maiores ou menores que o litro. Por exemplo, uma lata de refrigerante comporta menos que 1 litro, já uma caixa d’água pode ter capacidade para 2 mil litros, bem maior que um litro.

Conversão de medidas de capacidade A conversão de litro para seus múltiplos e submúltiplos pode ser feita de acordo com algumas relações: • 1 quilolitro (kl) = 1. 000 litros • 1 hectolitro (hl) = 100 litros • 1 decalitro (dal) = 10 litros • 1 litro = 1000 mililitros (ml) • 1 litro = 100 centilitros (cl) • 1 litro = 10 decilitros (dl) A conversão entre as medidas de capacidade também pode ser realizada com base no sistema de numeração decimal. Nesse caso, realiza-se uma multiplicação ou uma divisão por 10. Veja na tabela abaixo:

Os múltiplos são utilizados quando há quantidades maiores que o litro: • Decalitro (dal) • Hectolitro (hl) • Quilolitro (kl) Já os submúltiplos são utilizados quando há quantidades menores que o litro: • Decilitro (dl) • Centilitro (cl) • Mililitro (ml) OBS. : Relação entre as medidas de capacidade e volume O litro e o metro cúbico são medidas que medem capacidade. Em função disso, os múltiplos e submúltiplos dessas duas medidas podem ser relacionados: 1 metro cúbico (m³) corresponde à capacidade de 1000 litros. 1 decímetro cúbico (dm³) corresponde à capacidade de 1 litro. 1 centímetro cúbico (cm³) corresponde à capacidade de 1 mililitro (ml). Por exemplo, considere que uma piscina infantil de uma escola possui 10 m³ de volume, ou seja, a sua capacidade é de 10. 000 litros de armazenamento. Nessa mesma escola há uma garrafão de água com 2 dm² de volume, o que equivale a 2 l de água que podem ser comportados.

Agora que você já sabe como realizar a conversão entre as medidas. Veja abaixo a resolução de dois exemplos: Exemplo 1 - 60 ml de leite corresponde a quantos litros? Seguindo a tabela de conversão, podemos perceber que para converter de ml para l devemos dividir 60 ml três vezes por 10, que é o mesmo que dividir por 1. 000. Logo, 60/1. 000 = 0, 06 l Exemplo 2 - 7 da. L de gasolina corresponde a quantos decilitros? Com base no critério anterior, para converter de decalitro para decilitro devemos multiplicar 7 dal duas vezes por 10, isto é, multiplicar por 100. 7. 100 = 700 d. L

Questão 1: Um aluno de Ensino Médio vai até o açougue, a pedido de seus pais, comprar 5 kg de carne para um churrasco em sua casa. Além da carne, ele compra 8 litros de refrigerante para oferecer aos convidados. Qual das alternativas a seguir possui os valores da quantidade de carne e de refrigerante, respectivamente, nas unidades tonelada (t) e mililitro (m. L)? a) 0, 005 t e 0, 008 m. L b) 5000 t e 0, 008 m. L c) 0, 005 t e 8000 m. L d) 5000 t e 8000 m. L Questão 2: Sabendo-se que o peso de um satélite na Lua é de 3200 N, qual é a massa desse satélite na Terra? Dado: Adote g. TERRA = 10 m/s 2, g. LUA= 1, 6 m/s 2 a) 2000 kg b) 200 kg c) 20 kg d) 20000 kg

Questão 3: Uma das medidas agrárias mais comum é a arroba, denotada por @. Dessa forma, um gado tem o peso de 475 kg, sabendo-se que uma arroba corresponde a 15 kg, o peso desse gado em arroba é de aproximadamente: a) 30@ b) 31@ c) 32@ d) 45@ Questão 4: Sandra gasta 32, 5 l de gasolina por semana. Quanto gastará em 3 semanas?

Gabarito da questão 1: Letra c). O exercício fornece os valores 5 kg e 8 L, de massa e volume, respectivamente, e pede para que passemos essas unidades para tonelada e mililitro. Para isso, basta montar regras de três. Veja: • Para a massa: Sabe-se que 1 tonelada equivale à quantidade de 1000 kg. Dessa forma, a regra de três utilizada para transformar 5 kg em t é: � Para o volume: Sabe-se que 1 litro equivale à quantidade de 1000 m. L. Dessa forma, a regra de três utilizada para transformar 8 litros em m. L é:

Gabarito da questão 2: Letra A A massa do satélite é a mesma em qualquer local, assim, por meio da definição da força peso, pode-se determinar a massa desse satélite: P = m. g 3200 = m. 1, 6 m = 2000 kg Gabarito da questão 3: Resolução Alternativa C. Para fazer a conversão, basta dividirmos 475 por 15. 475 : 15 = 31, 66… Realizando o arredondamento: 32@. Gabarito da questão 4: Solução: 3 x 32, 5 l = 97, 5 litros Gastará 97, 5 litros