Time Series Analysis 1 What is a time

Time Series Analysis 1

What is a time series? A time series is any series of data that varies over time. For example Quarterly GDP of Laos Hourly price of stocks and shares Weekly quantity of beer sold in a pub Each time-series is one realization of a stochastic (i. e. random) process 2

Stationary Time Series Has constant Mean and constant Variance across time Has a theoretical covariance between values of Xt that depends only on the difference apart in time 3

5

6

7

8

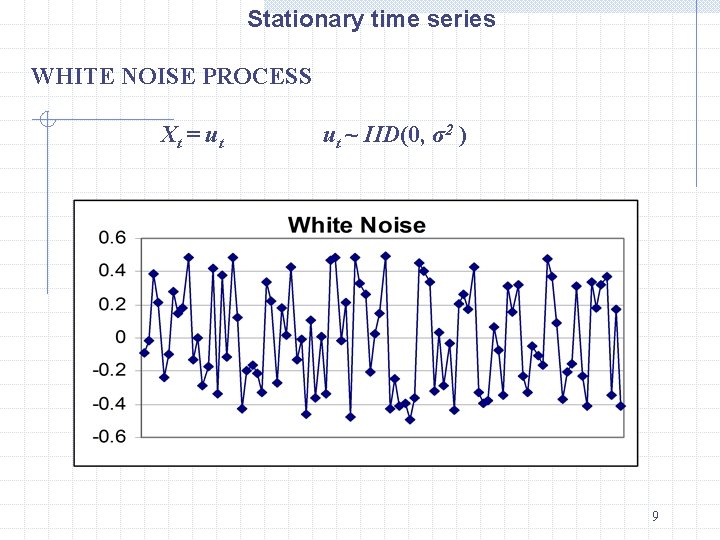
Stationary time series WHITE NOISE PROCESS X t = ut ut ~ IID(0, σ2 ) 9

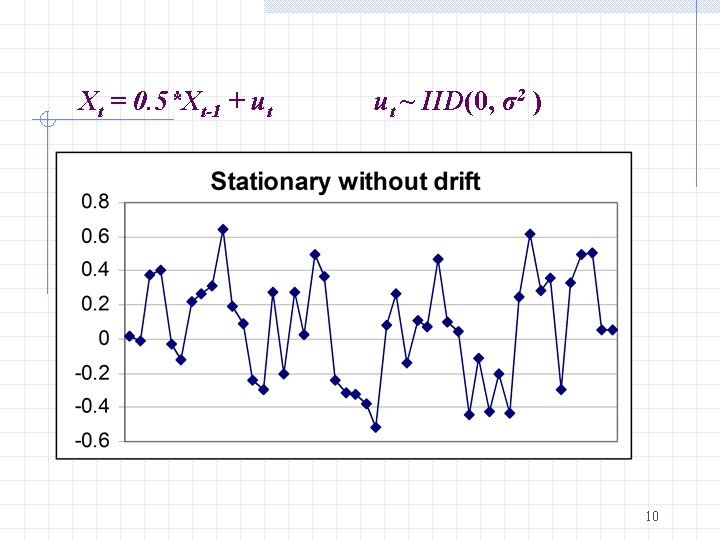
Xt = 0. 5*Xt-1 + ut ut ~ IID(0, σ2 ) 10

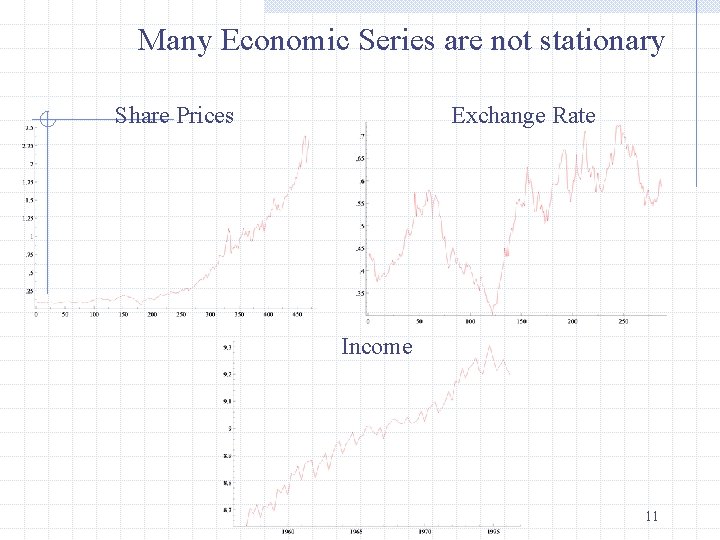
Many Economic Series are not stationary Share Prices Exchange Rate Income 11

Non Stationary Time Series There is no long-run mean for the timeseries and/or The variance is time dependent and goes to infinity as time approaches to infinity 12

Spurious Regression The results of classical econometric theory are derived under the assumption that variables of interests are stationary. A Spurious or Nonsensical relationship may result when one Non-stationary time series is regressed on one or more Non-stationary time series. 13

14

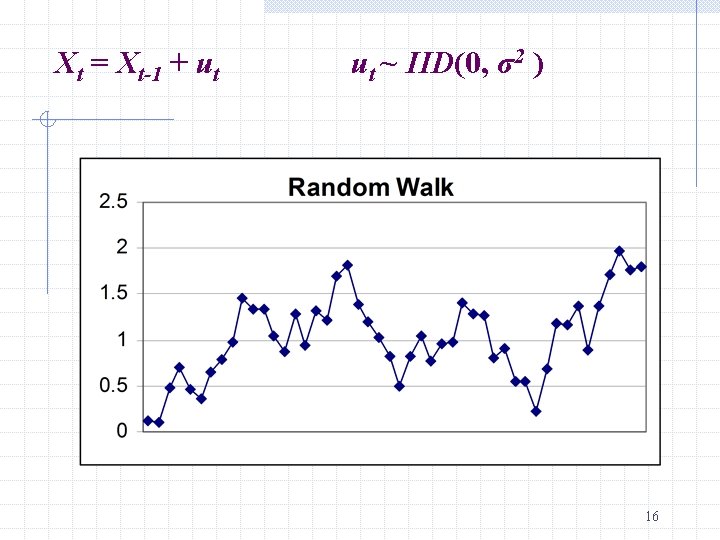
An example of Non-stationary time series RANDOM WALK Xt = Xt-1 + ut ut ~ IID(0, σ2 ) Xt = X 0 + u 1 + u 2 +…+ ut Variance: Var(Xt) = Var(X 0) + Var(u 1) +…+ Var(ut) = 0 + σ2 +…+ σ2 = t σ2 (variance is not constant through time) 15

Xt = Xt-1 + ut ut ~ IID(0, σ2 ) 16

17

What is a “Unit Root”? If a Non-Stationary Time Series Xt has to be “differenced” d times to make it stationary, then Xt is said to contain d “Unit Roots”. It is customary to denote Xt ~ I(d) which reads “Xt is integrated of order d” 19

Establishment of Stationarity Using Differencing of Integrated Series If Xt ~ I(1), then Zt = Xt – Xt-1 is Stationary If Xt ~ I(2), then Zt = Xt – Xt-1 – (Xt – Xt-2 ) is Stationary 20

Random Walks A random walk is as a unit root process A random walk process is “integrated of order one, [I(1)], ” meaning a first difference will be stationary, “I(0)”. 21

23

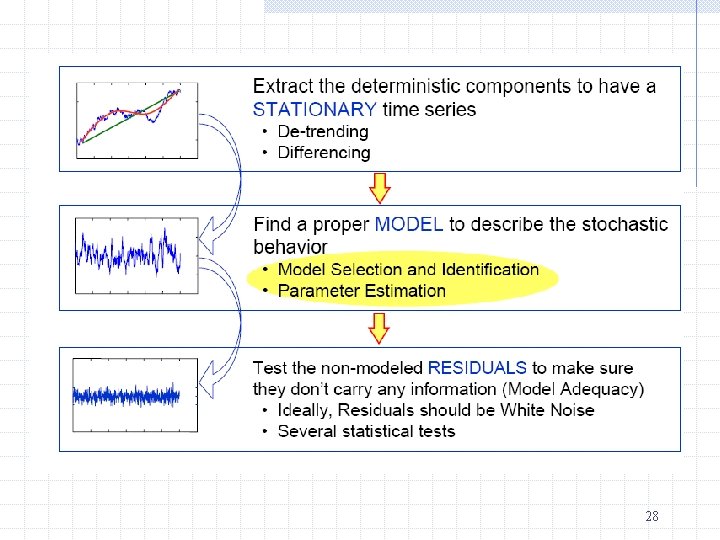
Removing trend and seasonality in a time-series Economic time series often have a trend One possibility to remove a linear trend involves regressing the series on t, which can be modeled as xt = a 0 + a 1 t + et Then analyze the residuals from the detrended series. 24

Seasonality Sometimes time-series data exhibits some seasonality. Example: Quarterly data on retail sales will tend to jump up in the 4 th quarter As with trends, the series can be seasonally adjusted by adding a set of seasonal dummies in the above regression. 25

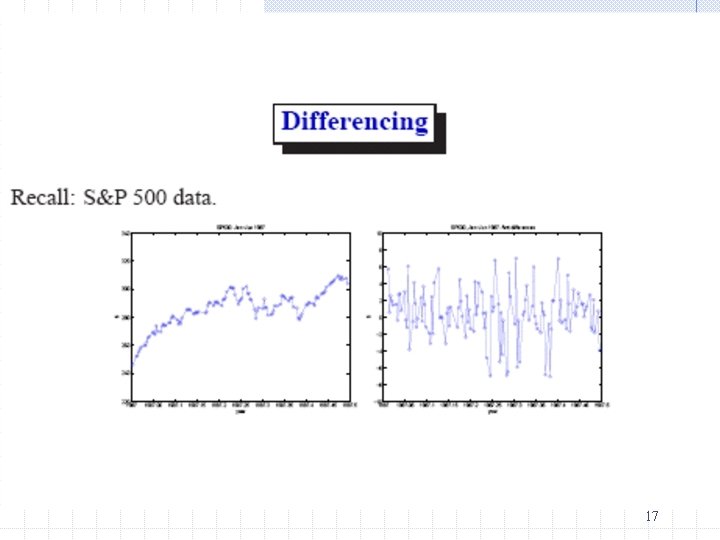
Alternatively, We can simply remove trend or seasonality by calculating first difference or seasonal difference. 26

A trending series or seasonal series cannot be stationary, since the mean is changing over time. After the adjustment, the remaining maybe stationary and can be analyzed. 27

28

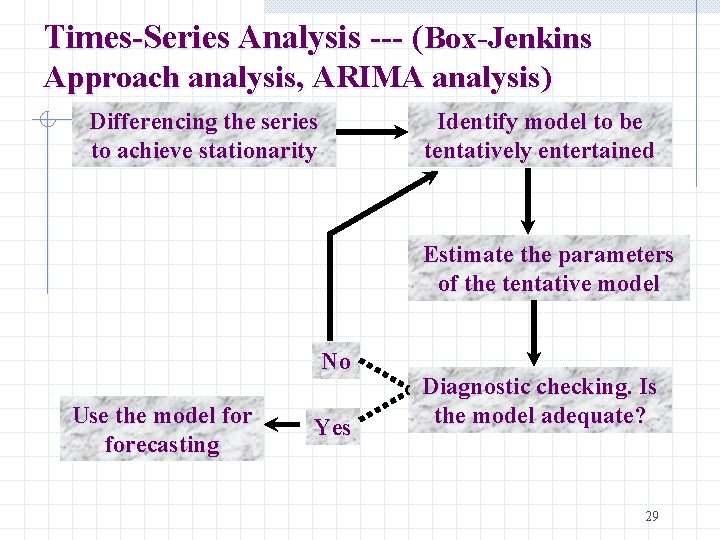
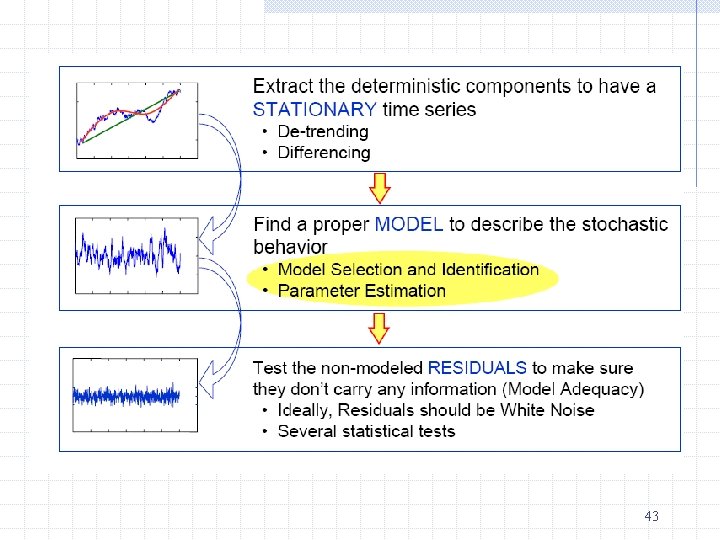
Times-Series Analysis --- (Box-Jenkins Approach analysis, ARIMA analysis) Differencing the series to achieve stationarity Identify model to be tentatively entertained Estimate the parameters of the tentative model No Use the model forecasting Yes Diagnostic checking. Is the model adequate? 29

ARIMA Analysis • We use an autoregressive integrated moving average (ARIMA) model to fit the data. • If time-series data is already stationary, can use autoregressive moving average (ARIMA) model to fit the data. 30

We will use ARMA model to fit a stationary time-series data. ARMA (p, q) refers to a model with p autoregressive terms and q moving average terms. An ARMA (p, q) process is a stationary process in the following form :

An AR(1) Process (ARMA(p=1, q=0)) An autoregressive process of order one [AR(1)] can be characterized as one where xt = rxt-1 + et , t = 1, 2, … with et being an iid sequence with mean 0 and variance se 2 For this process to be stationary, it must be the case that |r| < 1 33

Random Walks A random walk is an AR(1) model where r =1 A random walk series is not stationary. 34

An MA(1) Process (ARMA(p=0, q=1)) A moving average process of order one [MA(1)] can be characterized as one where xt = et + 1 et-1, t = 1, 2, … with et being an iid sequence with mean 0 and variance s 2 e This is a stationary sequence. Variables 1 period apart are correlated, but 2 periods apart they are not. 36

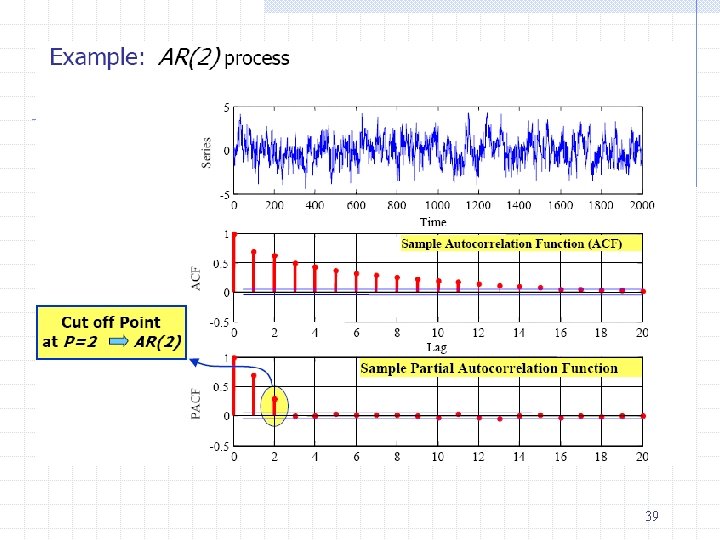
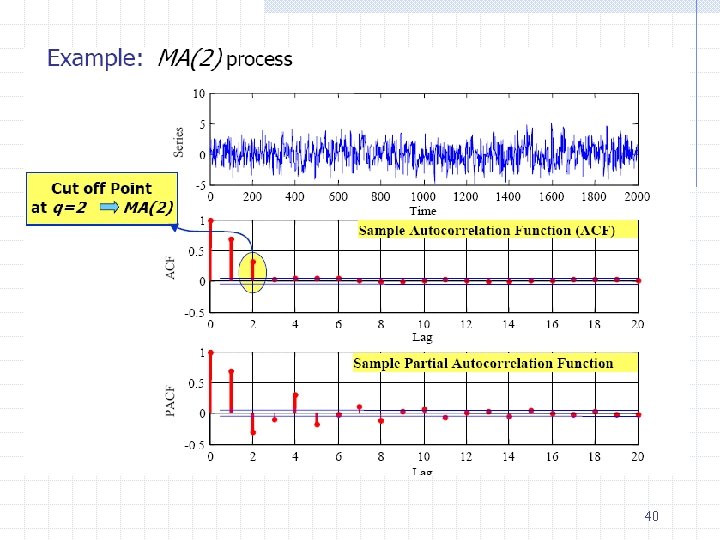
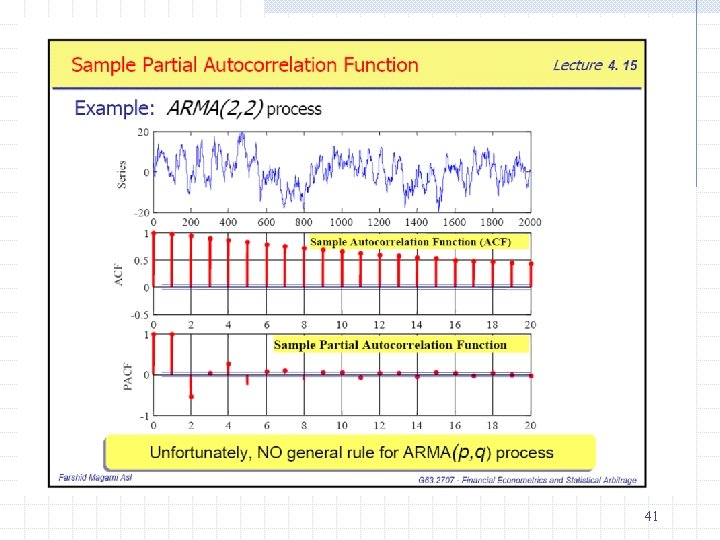
How to choose p and q? Check ACF and PACF graphs • Correlogram – graph showing the ACF and the PACF at different lags. • Autocorrelation function (ACF)- ratio of sample covariance (at lag k) to sample variance • Partial autocorrelation function (PACF) – measures correlation between (time series) observations that are k time periods apart after controlling for correlations at intermediate lags (i. e. , lags less than k). In other words, it is the correlation between Yt and Yt-k after removing the effects of intermediate Y’s. 37

Identifying the model by examining patterns of ACF and PACF Type of Model AR (p) MA (q) ARMA (p, q) Typical Pattern of ACF Typical Pattern of PACF Decays exponentially or Significant spikes with damped sine wave through lags p pattern or both Significant spikes Declines through lags q exponentially Exponential decay 38

39

40

41

Diagnostic Checking—Is our model good enough? How do we know that the model we estimated is a reasonable fit to the data? ü Check residuals after the modeling Rule of thumb: None of the ACF and the PACF are individually statistically significant Formal test: Ljung-Box Q is estimated autocorrelation at lag h. 42

43

Some issues in the time-series modeling üDo not know the underlying cause; we still do not understand why the series is behaving this or that way. üJudgmental decisions on the choice of AR, MA, p, q. Also, model identification requires large number of observations but often times-series data is not very long. üThe model you fitted in past data may not work well in current or future data. 44