tefan Stncescu Teoria reelelor Stefan Stncescu Proces Markov

Ştefan Stăncescu Teoria reţelelor Stefan Stăncescu

Proces Markov X - variabilă stochastică cu evoluţie continuă în timp X - este proces Markov staţionar de variaţie continuă în timp dacă starea ulterioară depinde numai de starea prezentă deci viitor(prezent) viitor | trecut – indepentente (Procese independente: Procese Markov limită starea ulterioară nu depinde nici de starea prezentă) Teoria reţelelor Stefan Stăncescu

Lanţ Markov Lanţul Markov este proces Markov X de valori discrete: valori discrete ale timpului t=0, 1, 2, 3, . . . (valori discrete numărabile) valori discrete ale variabilei aleatoare (stări discrete) Xn=v 0, v 1, . . . (valori finite numărabile la momentele de timp n) Starea i a lanţului Markov: Situaţia în care X=Xi Probabilitatea lanţului Markov de a trece din starea i a momentului anterior n-1 în starea j a momentului prezent n: pi, j = [ p(Xn=j) | Xn-1=i ] pi, j nu depinde de n; oricât se stă în i, cu aceeaşi probabilitate se trece în j. Teoria reţelelor Stefan Stăncescu

Parcurgerea unui lanţ de stări Lanţ de stări (i 0, i 1, i 2, . . . , in): p(X 0=i 0, X 1=i 1, . . . , Xn=in) = p(X 0=x 0)*pi 0 i 1*pi 1 i 2*. . . *pin-1 in probabilitate lanţ - produsul probabilităţilor tuturor tranziţiilor Trecerea din starea i în starea j prin starea k pij=∑k pikpkj (Trecereaîn j prin fiecare k se insumează ca probabilitate) Matricea stochastică a lanţului Markov: P = { pij }0<= i, j <= n-1 P 2 = { ∑k pikpkj} cu 1 hop în k Teoria reţelelor Stefan Stăncescu

Pn cu n hopuri între i şi j Pn = Pm*Pn-m p(n)ij = ∑k p(m)ik * p(n-m)kj (Chapman- Kolmogorov) Probabilitatea de tranziţie prin n hopuri, trecând după m hopuri prin nodul k Probabilitatea ca lanţul Markov să fie în starea i la momentul n: π(n)i = p(Xn=i), i=1, 2, . . . Vectorul de probabilitate pentru toate starile lanţului Markov: Π(n)=(π(n)0, π(n)1, π(n)2, . . . ) Teoria reţelelor Stefan Stăncescu

Din legea probabilităţii totale, la momentul 1: p(X 1= i) = ∑k p(X 1=i| X 0= k) * p(X 0= k), i=1, 2, . . . π(1)i = p(X 1=i) = ∑k p(X 1=i| X 0= k) * p(X 0= k), i=1, 2, . . . π(1)i = ∑k pk, i * π(0)k, i=1, 2, . . . Π(1) = Π(0) * P şi Π(2) = Π(1) * P. . Π(n) = Π(n-1) * P Înlocuind, obţinem probabilităţile stărilor la momentul n: Π(n) = Π(0) * P(n) Teoria reţelelor Stefan Stăncescu

Teorema Kolmogorov Lanţurile Markov ajung la staţionaritate. Se ajunge la o • distribuţie stabilă de stări πi • distribuţie independentă de starea iniţială πi = limn→∞ π(n)i Π=(π0, π1, π2, . . . ) Ecuaţia de staţionaritate: Π=Π*P sau Π(P - I)=0 Aflarea soluţiei de staţionaritate, adică aflarea vectorului distribuţiei de stări πi, din sistemul de ecuaţii: πj=∑iπi pij j=1, 2, . . . condiţia de echilibru global ∑ jπ j= 1 Tj=1/πj interval mediu de timp în care procesul stă în starea j Teoria reţelelor Stefan Stăncescu

Echilibru global ∑i pji= 1 ∑i πj pji trecerea din j trebuie sa ducă sigur într-o stare oarecare probabilitatea ca din starea posibilă j să se ajungă în toate celelalte stări (ieşiri din j) ∑i πi pij probabilitatea ca din toate stările să se ajungă în j (intrări) La echilibru, fluctuaţia totală e nulă şi ieşirile = intrările. Pentru fiecare j cîte o ecuaţie (n ecuaţii, din care una e nenecesară) ∑i πj pji = ∑i πi pij Plus ecuaţia de normalizare (în locul ultimei ecuaţii) ∑i πj = 1 (sistemul e sigur într-una din stări) Matricial, normalizarea se scrie: Π*e. T=1, unde e=(1, 1, . . . 1), şi cu matricea E=(e. T. . . e. T), rescriem Π*E=e Teoria reţelelor Stefan Stăncescu

Echilibru global(continuare) Reluînd ecuaţia de echilibru Π=Π*P, adică Π*(P-I)=0, cu noua ecuaţie Π*E=e, se obţine Π*(P+E-I)=e cu rezolvarea vectorului probabilităţilor de stari la staţionaritate Π=e*(P+E-I)-1 Am găsit soluţia de staţionaritate Teoria reţelelor Stefan Stăncescu

Trecerea spre echilibru la lanţuri Markov cu timp continuu Densitatea de probabilitate de a trece din starea i în j în momentul t (viteza de modificare a probabilităţii de trecere din starea i în j): qij(t) = limΔt→ 0 P{Xt+Δt =j|Xt =i}/Δt i≠j La procese Markov qij(t) nu depind de timp. Densitatea de probabilitate de a părăsi starea i (viteza de modificare a probabilităţii de a părăsi starea i): qi = ∑j≠i qij Fie qi, i = - qi Cu qi, j definite mai sus construim matricea densităţii de probabilitate: Q = { qij } Teoria reţelelor Stefan Stăncescu

Trecerea spre echilibru la lanţuri Markov cu timp continuu (cont) Cu densităţile de probabilitate din matricea Q se stabilesc evoluţiile în timp ale probabilităţilor de trecere din starea i în j: dΠ(t)/dt = Π(t)*Q cu soluţia Π(t) = Π(0)*e. Qt La stabilizare, viteza de modificare a probabilităţilor este 0 dΠ(t)/dtt→∞ = Π(t)t→∞*Q = 0 Π(t)t→∞= Π =(π0, π1, π2, . . . ) unde Π este constantă. Deci, la stabilizare, condiţia de echilibru este: Π* Q = 0 Teoria reţelelor Stefan Stăncescu

Echilibrul fluxurilor de probabilitate Din linia j a Π* Q = 0 se deduce qj πj=∑i≠jπi qij iar deoarece qj =∑i≠j qji rezultă ∑i≠j πj qji =∑i≠j πi qij este fluxul de probabilitate de trecere din i în j Deci toate variaţiile de probabilităţi de trecere dinspre starea j înspre celelalte echilibrează toate variaţiile de probabilităţi de trecere înspre starea j dinspre celelalte → Echilibru global în periada de tranziţie spre stabilitate Teoria reţelelor Stefan Stăncescu

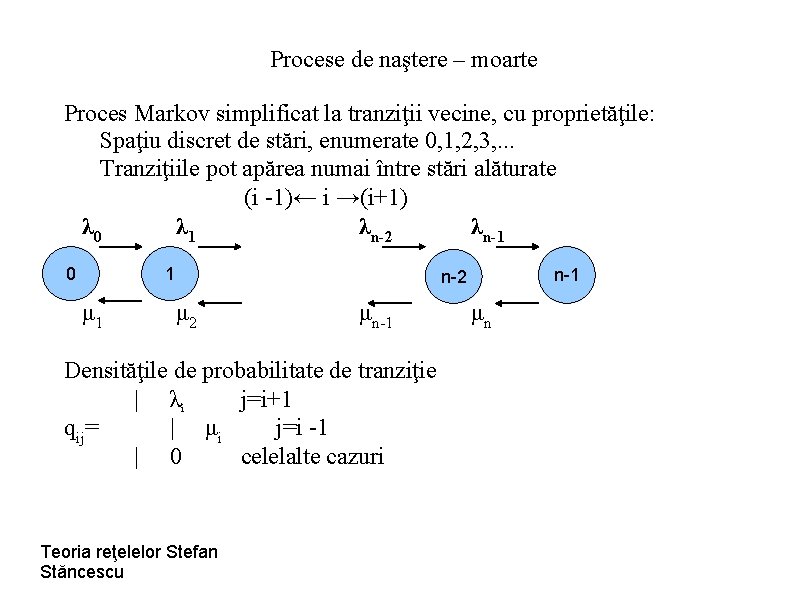
Procese de naştere – moarte Proces Markov simplificat la tranziţii vecine, cu proprietăţile: Spaţiu discret de stări, enumerate 0, 1, 2, 3, . . . Tranziţiile pot apărea numai între stări alăturate (i -1)← i →(i+1) λ 0 λ 1 λn-2 λn-1 0 1 μ 1 n-2 μ 2 μn-1 Densităţile de probabilitate de tranziţie | λi j=i+1 qij= | μi j=i -1 | 0 celelalte cazuri Teoria reţelelor Stefan Stăncescu μn

Procese de naştere – moarte(continuare) La echilibru: λi πi = μi+1 πi+1 = (λi / μi+1) πi πk = (λk-1 λk-2. . . λi 0 / μkμk-1. . . μ 1) * π0 = Πi=0 k-1 (λi / μi+1) * π0 ∑ 0∞ πk = 1 sau π 0 + ∑ 1∞ π k = 1 din care se obţine, înlocuind πk şi extrăgând π0: π0 = 1 / [1+∑ 1∞Πi=0 k-1 (λi / μi+1)] şi apoi ceilalţi πk , probabilităţile tuturor stărilor la staţionaritate. Teoria reţelelor Stefan Stăncescu

Procese de naştere – moarte(continuare 2) Din ecuaţia evoluţiei spre stabilitate: dΠ(t)/dt = Π(t)*Q d πi (t)/dt = - ( λi + μi ) πi(t) + ( λi+1 ) πi-1(t) + μi+1 πi+1(t) 1 d π0 (t)/dt = - ( λ 0 + μ 0 ) π0(t) + μ 1 π1(t). Teoria reţelelor Stefan Stăncescu

Procese de moarte Proces Markov simplificat la tranziţii vecine, cu proprietăţile: Spaţiu discret de stări, enumerate 0, 1, 2, 3, . . . Tranziţiile pot apărea numai între stări alăturate (i -1)← i ←(i+1) 0 1 μ 2μ n-1 n-2 (n-1)μ nμ Densităţile de probabilitate de tranziţie qij= | μi= iμ j=i -1 | 0 celelalte cazuri Se porneşte din starea πn (0) = 1, cu celelalte πi (0) = 0 i≠n Teoria reţelelor Stefan Stăncescu

Procese de moarte(continuare) Din ecuaţia evoluţiei spre stabilitate: dΠ(t)/dt = Π(t)*Q d πi (t)/dt = ( i+1) μ πi+1(t) - i μ πi(t) d πn i = n+1, n-2, . . . 1, 0 (t)/dt = - n μ πn(t) πn (t) = e - n μt i μ πi(t) + d πi (t)/dt = ( i+1) μ πi+1(t) i μ e i μt πi(t) + e d (e i μt (t)/dt = ( i+1) μ e i μt πi+1(t) i = n+1, n-2, . . . 1, 0 πi(t))/dt = ( i+1) μ e i μt πi+1(t) Teoria reţelelor Stefan Stăncescu i μt i = n+1, n-2, . . . 1, 0 d πi

Procese de moarte (continuare 2) e i μt πi(t) = ( i+1) μ ∫ 0 te i μt' π i+1(t')dt' i = n+1, n-2, . . . 1, 0 i=n-1 e (n-1)μt πn-1(t) = n μ ∫ 0 te (n-1) μt' πn(t')dt cu πn (t') = e - n μt' ∫ 0 te (n-1) μt' e - n μt'dt' = ∫ 0 te - μt'dt' = 1/ μ (1 - e -μt ) e (n-1)μt πn-1(t) = n (1 - e -μt ) πn-1(t) = n * e -(n-1)μt (1 - e -μt ) πi(t) = Cni [e -μt ]i (1 - e -μt )(n-i) πi(t)→ 1 (i≠ 0), π0(t) → 0 Teoria reţelelor Stefan Stăncescu Distribuţie binomială

Procese de naştere Proces Markov simplificat la tranziţii vecine, cu proprietăţile: Spaţiu discret de stări, enumerate 0, 1, 2, 3, . . . Tranziţiile pot apărea numai între stări alăturate (i -1)→ i →(i+1) λ λ 0 1 n-2 n-1 Densităţile de probabilitate de tranziţie | λ j=i+1 qij= | 0 celelalte cazuri Se porneşte din starea π0 (0) = 1, cu celelalte πi (0) = 0 Teoria reţelelor Stefan Stăncescu i≠ 0

Procese de naştere(continuare) Din ecuaţia evoluţiei spre stabilitate: dΠ(t)/dt = Π(t)*Q d πi (t)/dt = - λ πi (t) + λ μ πi-1(t) d π0 i = n, n-1, . . . 2, 1 (t)/dt = - λ πn(t) π0 (t) = e -λt λ πi(t) + d πi(t)/dt = λ πi-1(t) i = n, n-1, . . . 2, 1 e λtλ πi(t) + e λtd πi(t)/dt = λe λt πi-1(t) i = n, n-1, . . . 2, 1 d(e λt πi(t))/dt = λe λt πi-1(t) i = n, n-1, . . . 2, 1 Teoria reţelelor Stefan Stăncescu

Procese de naştere (continuare 2) e λt πi(t) = λ ∫ 0 te λt'' πi-1(t')dt' i = n, n-1, . . . 2, 1 i=1 e λt π1(t) = λ ∫ 0 te λt'' π0(t')dt' π1(t) = λe -λt ∫ 0 te λt'' π0(t')dt' Cu π0 (t) = e -λt π1(t) = λe -λt ∫ 0 tdt' π1(t) = λte -λt πi(t) = (λt)ie -λt/i! Teoria reţelelor Stefan Stăncescu Distribuţie Poisson

Teorema Little Printr-un nod, într-un interval dat 0 - t, trec N pachete N - nr. de pachete care trec prin nod în 0 - t n - număr mediu de pachete care stau în nod S - timp total de aşteptare al pachetelor care trec în 0 - t T - timp mediu aşteptare în nod pentru un pachet λ - frecvenţa de sosire/plecare a pachetelor - trafic T=S/N n=S/t =TN/t λ = N / t = n /T n=λT Teorema Little: Traficul este dat de nr mediu de pachete aşteptând în nod / timp mediu de aşteptare în nod sau nr. mediu de pachete aşteptând în nod este timp mediu de aşteptare în nod * trafic Teoria reţelelor Stefan Stăncescu

Exemplu la teorema Little 150 convorbiri telefonice / oră – trafic prin nod ( λ ) 3 minute durata medie a unei convorbiri - timp petrecut in nod ( T ) n = λ T Teorema Little n = nr de convorbiri în nod (simultane) n = 150 apeluri/60 min * 3 min = 15/2 apeluri = = 7, 5 convorbiri simultane, în medie, prin nod Teoria reţelelor Stefan Stăncescu

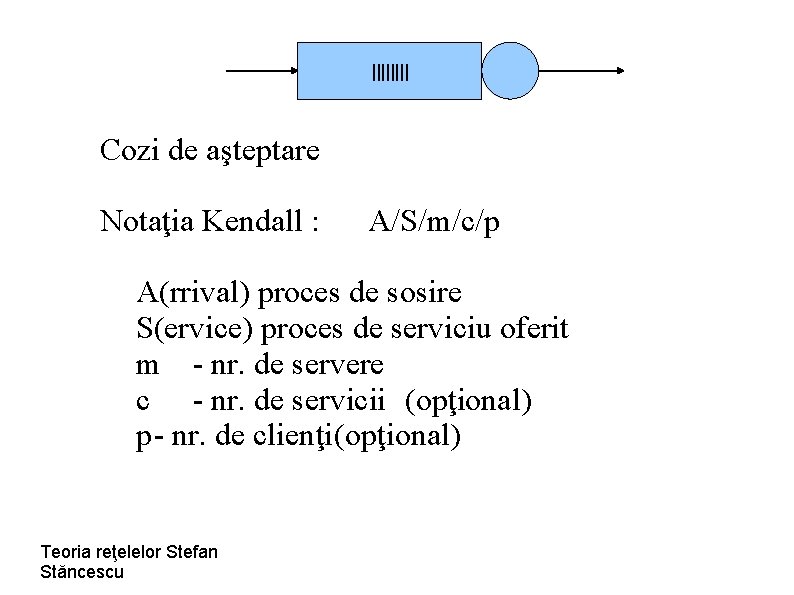
|||| Cozi de aşteptare Notaţia Kendall : A/S/m/c/p A(rrival) proces de sosire S(ervice) proces de serviciu oferit m - nr. de servere c - nr. de servicii (opţional) p- nr. de clienţi(opţional) Teoria reţelelor Stefan Stăncescu

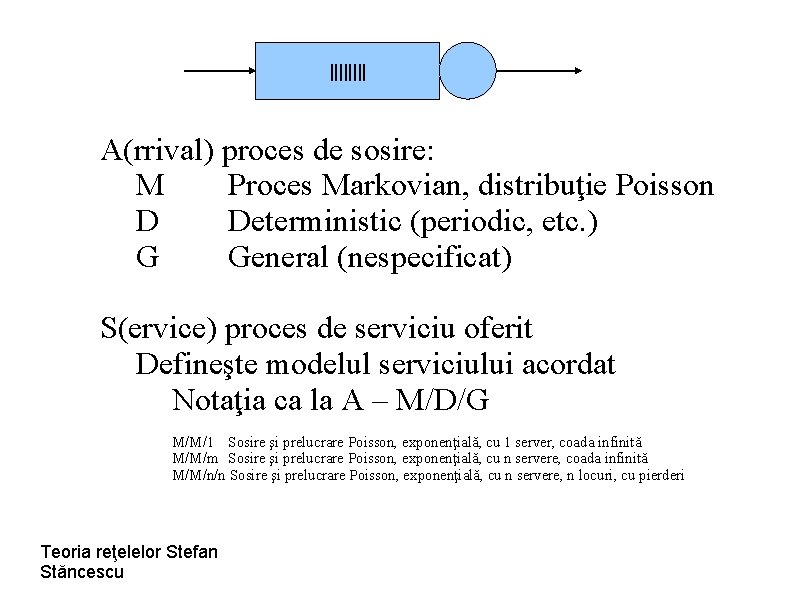
|||| A(rrival) proces de sosire: M Proces Markovian, distribuţie Poisson D Deterministic (periodic, etc. ) G General (nespecificat) S(ervice) proces de serviciu oferit Defineşte modelul serviciului acordat Notaţia ca la A – M/D/G M/M/1 Sosire şi prelucrare Poisson, exponenţială, cu 1 server, coada infinită M/M/m Sosire şi prelucrare Poisson, exponenţială, cu n servere, coada infinită M/M/n/n Sosire şi prelucrare Poisson, exponenţială, cu n servere, n locuri, cu pierderi Teoria reţelelor Stefan Stăncescu

Sisteme cu pierderi (0 locuri de aşteptare M/M/n/n) daca serverele sunt ocupate, orice alte sosiri se pierd Rezultă trafic blocat pe timp de blocare şi raport trafic blocat/trafic total Presupuneri: sosiri Poisson independente identic (normal) distribuite Rezultă proces Markov naştere şi moarte, cu λ - frecvenţa sosirilor μ - frecvenţa serviciilor n - servere în sistem Teoria reţelelor Stefan Stăncescu

Sisteme cu pierderi (0 locuri de aşteptare M/M/n/n) λ 0 λ λ 1 μ 2μ λ n-1 n-2 (n-1)μ nμ λ πj-1 =j μ πj cu a = λ /μ πj = (a / j) πj-1 πj = (aj / j!) π0 j=0, 1, . . . , n Dar ∑ 0 nπj =1 π0 = 1/ ( 1 + a/1! +. . . + an / n!) = 1/ ∑ 0 nai/i! πi = (aj/j!)/ ∑ 0 n(ai/i!) Formula Erlag – j=n π0 → e-a dacă n → ∞ Teoria reţelelor Stefan Stăncescu

Sisteme cu pierderi (M/M/n/n) - exemplu 4/6 modem-uri la trafic de intensitate a = 2 erl (a = λ / μ) E(n, a) = πn = (an/n!)/ ∑ 0 n(ai/i!) Formula Erlag E(4, 2) = 2/21 = 0, 095 = 9, 5 % E(6, 2) = 4/331 = 0, 012 = 1, 2 % Deci folosind 1, 5 (6/4) mai multe echipamente obţinem de 8 ori (9, 5/1, 2) mai mică probabilitatea de blocare. Teoria reţelelor Stefan Stăncescu

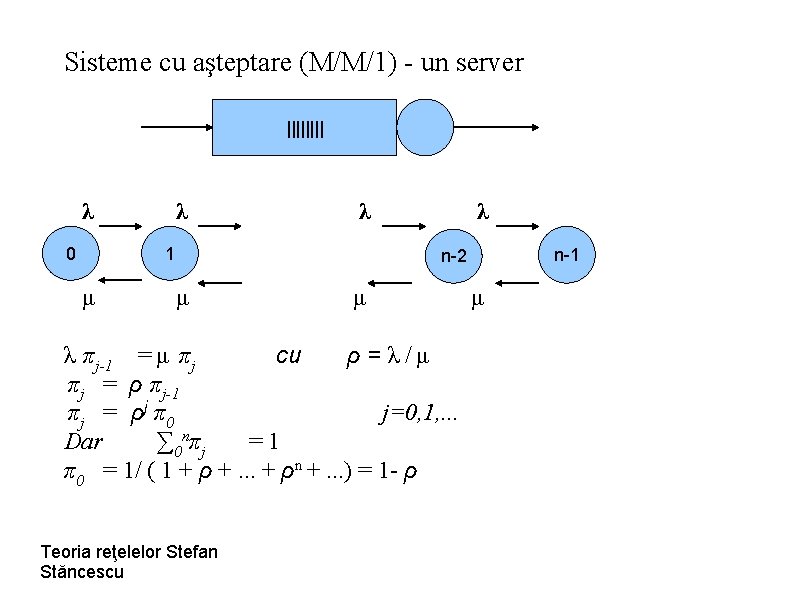
Sisteme cu aşteptare (M/M/1) - un server |||| λ 0 λ λ 1 μ λ n-1 n-2 μ μ λ πj-1 = μ πj cu ρ = λ /μ πj = ρ πj-1 π j = ρj π 0 j=0, 1, . . . Dar ∑ 0 nπj =1 π0 = 1/ ( 1 + ρ +. . . + ρn +. . . ) = 1 - ρ Teoria reţelelor Stefan Stăncescu μ

Sisteme cu aşteptare (M/M/1) |||| π0 este probabilitatea ca serverul să fie liber = 1 - ρ Probabilitatea ca serverul să fie ocupat = ρ πn = P(N=n) = (1 - ρ) * ρn distribuţie geometrică Teoria reţelelor Stefan Stăncescu

Sisteme cu aşteptare (M/M/1) |||| Fie N numărul mediu de clienţi în sistem N = ∑ 0∞i πi = (1 - ρ)∑ 0∞ (i ρi)= ρ (1 - ρ)∑ 0∞ (i ρi-1) = = ρ (1 - ρ)d/d ρ (∑ 0∞ ρi) = ρ (1 - ρ)d/dρ(1/(1 - ρ)) = ρ /(1 -ρ) N = ρ + ρ2 /(1 -ρ) ρ clienţi în server + ρ2 /(1 -ρ) clienţi în aşteptare Probabilitatea ca sunt cel puţin n clienţi în nod P(N>=n) = ∑n∞ πi = (1 - ρ)∑n∞ ρi = (1 - ρ) ρn ∑ 0∞ ρi = ρn Teoria reţelelor Stefan Stăncescu