SUJETS SPCIAUX EN INFORMATIQUE I PIF6003 Contenu du

SUJETS SPÉCIAUX EN INFORMATIQUE I PIF-6003

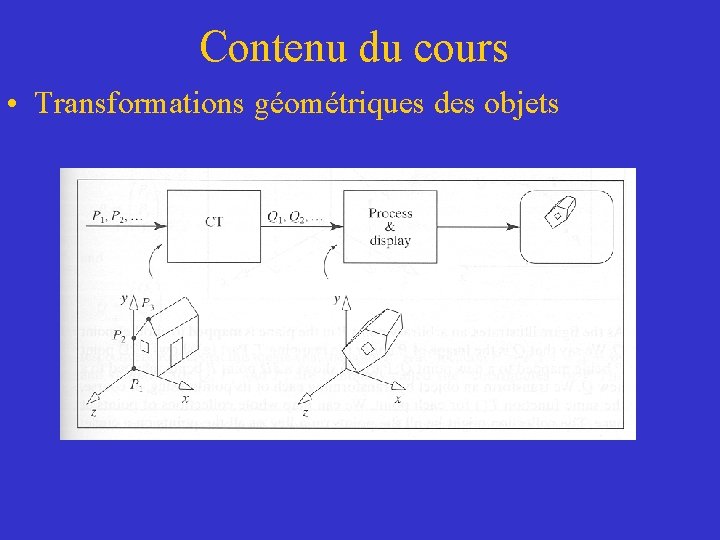
Contenu du cours • Transformations géométriques des objets – Transformations 2 D – Transformations entre systèmes de coordonnées – Transformations 3 D – Utilisation des transformations dans un programme – Introduction au processus de visualisation avec Open. GL

Contenu du cours • Transformations géométriques des objets

Transformations géométriques 2 D de base • Translation – La translation d’un point 2 D s’effectue par l’addition des distances de décalage tx et ty aux coordonnées d’origine du point (x, y) permettant son déplacement à la position (x’, y’)

Transformations géométriques 2 D de base • Translation – Sous forme matricielle

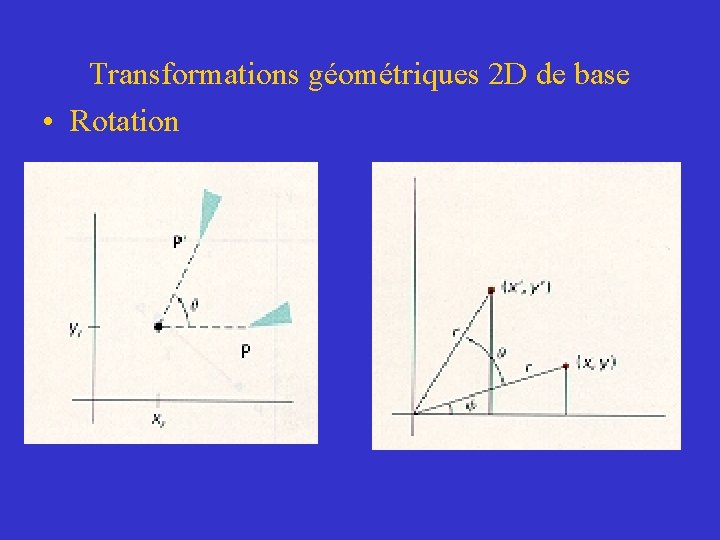
Transformations géométriques 2 D de base • Rotation – Une rotation est appliquée sur un objet en le déplaçant selon une trajectoire circulaire – Nous devons spécifier un angle de rotation ( ) et la position (xr, yr) du pivot – SI (xr=0, yr=0)

Transformations géométriques 2 D de base • Rotation

Transformations géométriques 2 D de base • Rotation – Sous forme matricielle avec

Transformations géométriques 2 D de base • Rotation – Par rapport à un pivot TRANSLATION Rotation suivi d’une translation

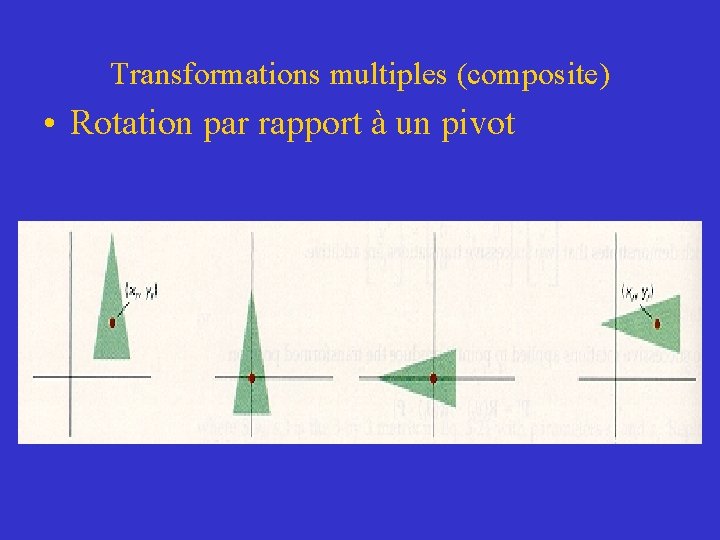
Transformations géométriques 2 D de base • Rotation – Par rapport à un pivot 1) Translation T(-xr, -yr) 2) Rotation d’un angle 3) Translation T(xr, yr)

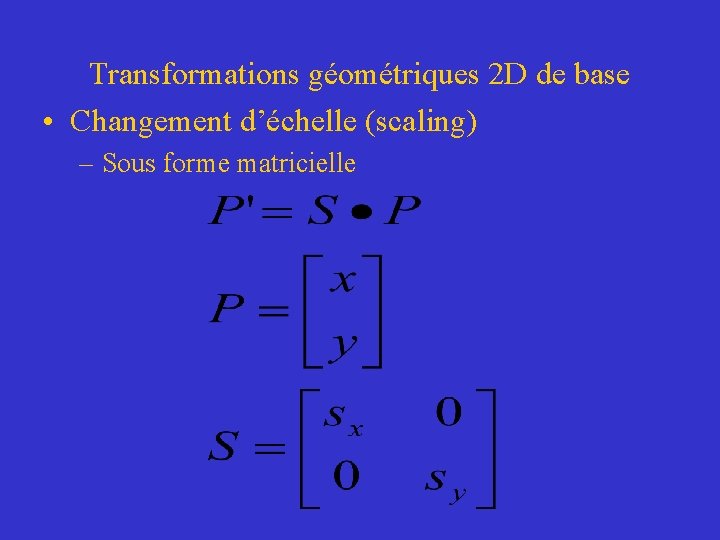
Transformations géométriques 2 D de base • Changement d’échelle (scaling) – Changement des dimensions d’un objet

Transformations géométriques 2 D de base • Changement d’échelle (scaling) – Sous forme matricielle

Transformations géométriques 2 D de base • Changement d’échelle (scaling) – Par rapport à un point de référence Scaling suivi d’une translation

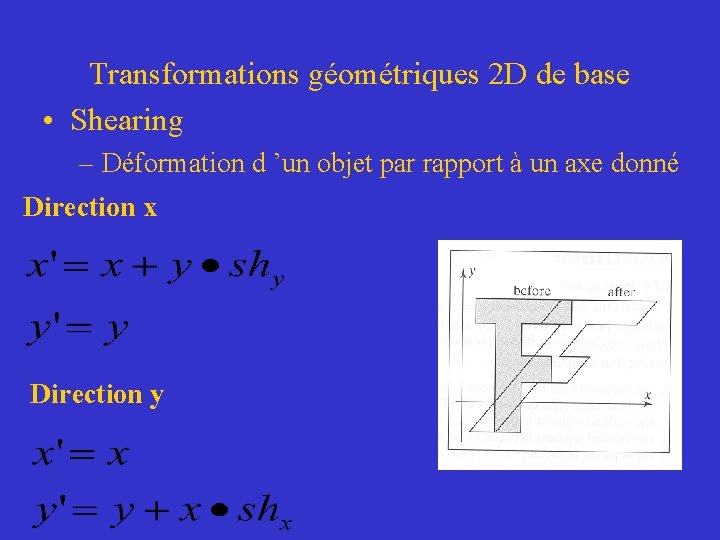
Transformations géométriques 2 D de base • Shearing – Déformation d ’un objet par rapport à un axe donné Direction x Direction y

Transformations géométriques 2 D de base • Shearing – Sous forme matricielle (Direction x)

Transformations multiples (composite) • Représentation matricielle et coordonnées homogènes – Dans plusieurs applications en graphisme des séquences de transformations graphiques doivent être générées – Les représentations matricielles servent de base pour modéliser de façon efficace ces séquences de transformations – Les transformations de base peuvent s’écrire Où M 1 est une matrice 2 X 2 et M 2 une matrice 2 X 1

Transformations multiples (composite) • Divers cas – Translation: • M 1: matrice identité • M 2: terme translationnel – Rotation: • M 1: matrice de rotation • M 2: terme translationnel (pivot) – Scaling: • M 1: matrice des changements d’échelle • M 2: terme translationnel (point de référence)

Transformations multiples (composite) • Une séquence de transformations S-R-T s’effectue: – scaling des coordonnées des objets – rotation des coordonnées transformées (après scaling) – translation des coordonnées (après rotation) • La combinaison de ces transformations permet d’améliorer l’efficacité en éliminant le terme additif M 2

Transformations multiples (composite) • Pour combiner les termes multiplicatifs et translationnels il faut utiliser une forme matricielle M 1 de 3 X 3 • Dans ce contexte nous pouvons représenter toutes les transformations sous forme de multiplication matricielle • Il faut par contre modifier la représentation matricielle des coordonnées des points constituant nos objets

Transformations multiples (composite) • Les coordonnées cartésiennes (x, y) sont alors représentées sous forme homogène (xh, yh, h) ou x=xh/h et y=yh/h • Alors une représentation en coordonnées homogènes généralisée peut aussi être déduite sous la forme (h x, h y, h) • Nous choisissons par simplicité h=1, chaque position est alors représentée en coordonnées homogènes par (x, y, 1)

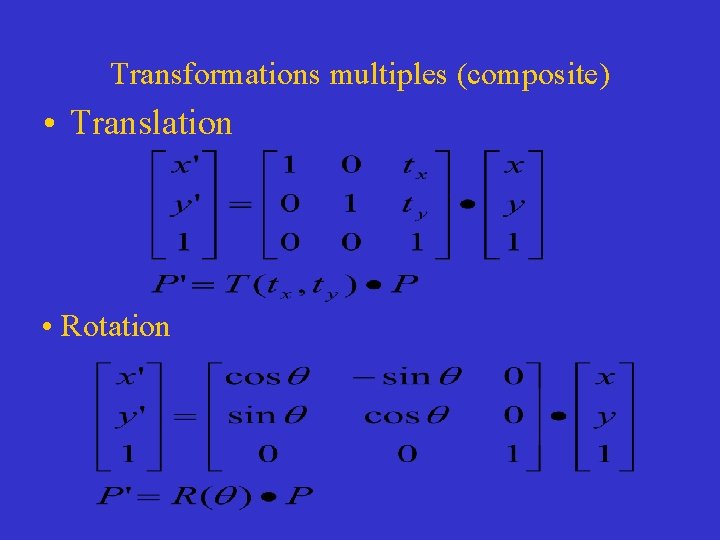
Transformations multiples (composite) • Translation • Rotation

Transformations multiples (composite) • Scaling

Transformations multiples (composite) • Shearing Direction x: SH(shx=0, shy) Direction y: SH(shx, shy=0)

Transformations multiples (composite) • Sachant que la multiplication matricielle est associative, les transformations successives sont alors représentées par une matrice 3 X 3 découlant de la concaténation des matrices individuelles • 2 translations successives (tx 1, ty 1), (tx 2, ty 2)

Transformations multiples (composite) • Cette transformation s’écrit

Transformations multiples (composite) • 2 rotations

Transformations multiples (composite) • 2 scaling

Transformations multiples (composite) • Rotation par rapport à un pivot

Transformations multiples (composite) • Matrice des transformations

Transformations multiples (composite) • Scaling avec un point de référence

Transformations multiples (composite) • Matrice des transformations

Transformations multiples (composite) • Forme générale • Complexité 4 X et + VS 9 X 6 +

Transformations multiples (composite) • Par exemple, si un objet doit subir un changement d’échelle et une rotation par rapport au point (xc, yc) et par la suite une translation, la matrice composite devient

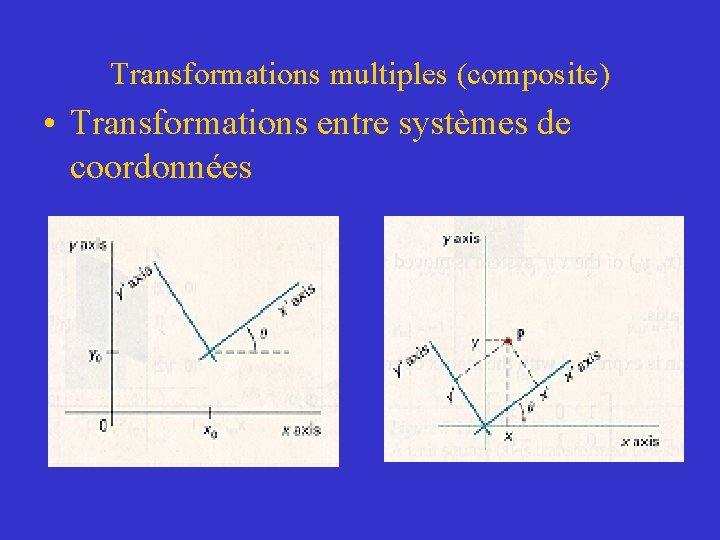
Transformations multiples (composite) • Transformations entre systèmes de coordonnées – Un objet quelconque peut être défini dans un système de coordonnées cartésien du monde (ex: scène du monde) mais les coordonnées du monde doivent être transformées au préalable pour permettre le positionnement de cet objet par rapport au système de coordonnées de l’écran avant son affichage

Transformations multiples (composite) • Transformations entre systèmes de coordonnées – Pour transformer la description d’un objet d’un système de coordonnées x y à x’y’ nous devons effectuer une transformation qui doit permettre la superposition des axes du système x’y’ sur ceux du système xy • Translation T(-x 0, -y 0) • R(- )

Transformations multiples (composite) • Transformations entre systèmes de coordonnées

Transformations multiples (composite) • Transformations entre systèmes de coordonnées

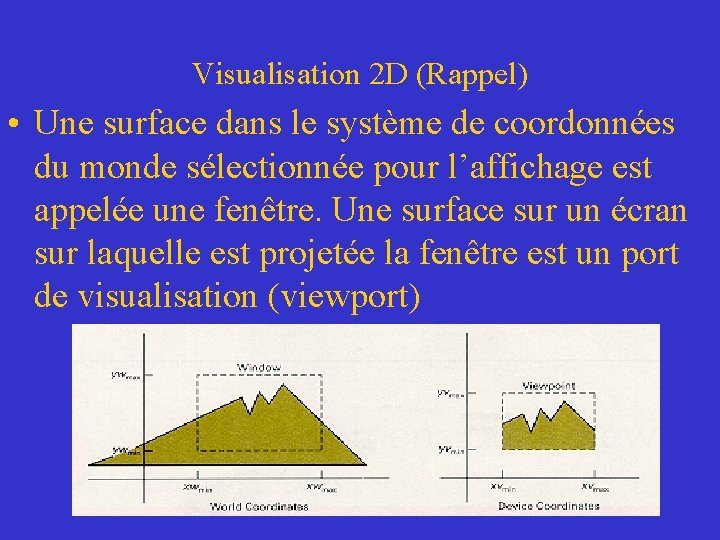
Visualisation 2 D (Rappel) • Une surface dans le système de coordonnées du monde sélectionnée pour l’affichage est appelée une fenêtre. Une surface sur un écran sur laquelle est projetée la fenêtre est un port de visualisation (viewport)

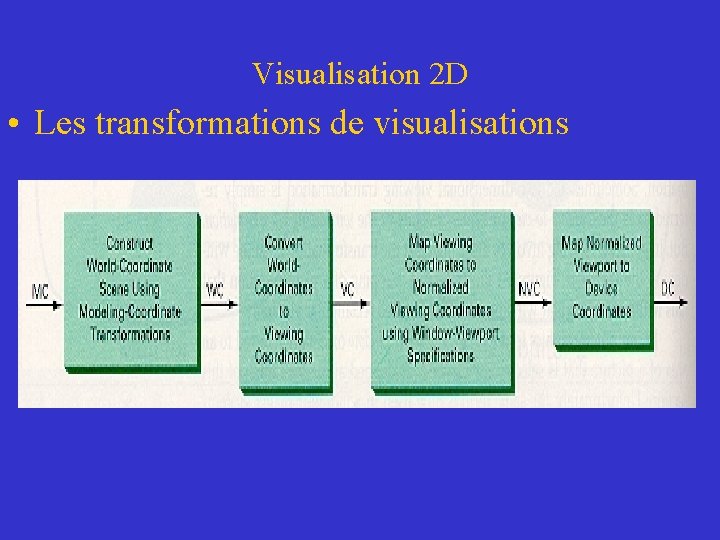
Visualisation 2 D • Les transformations de visualisations

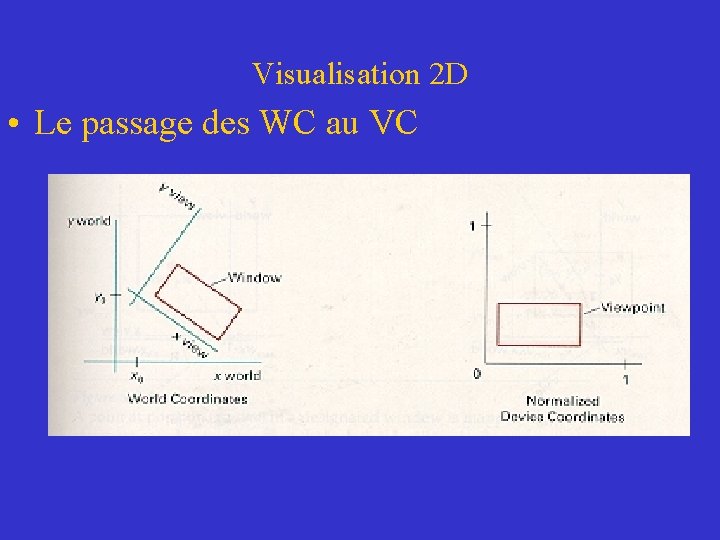
Visualisation 2 D • Le passage des WC au VC

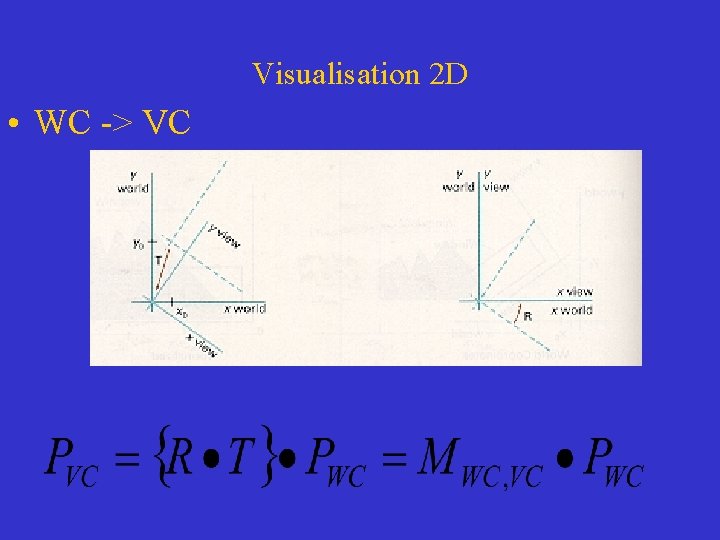
Visualisation 2 D • WC -> VC

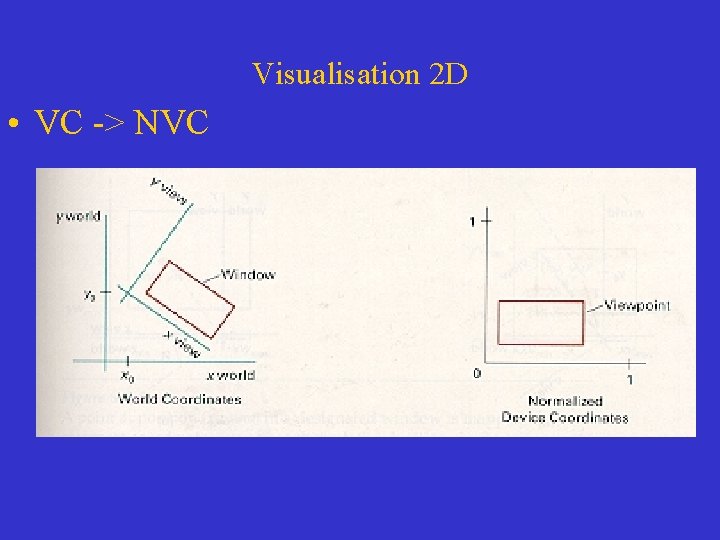
Visualisation 2 D • VC -> NVC

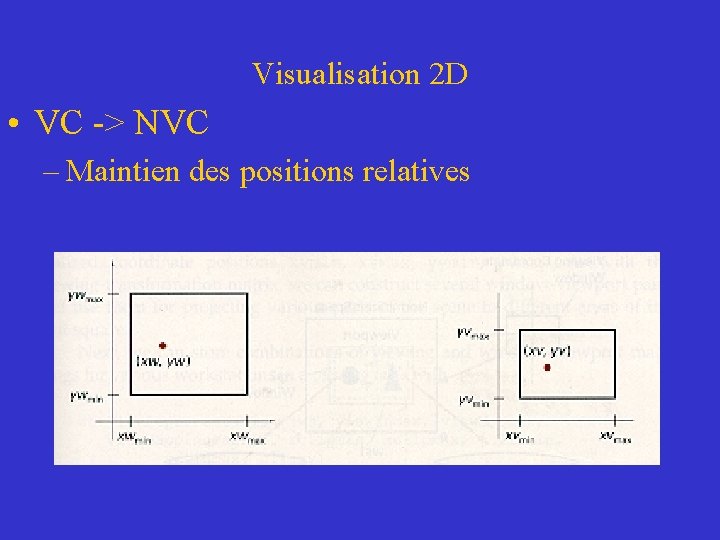
Visualisation 2 D • VC -> NVC – Pour maintenir les mêmes positions relatives dans les deux représentations nous devons savoir v: viewport w: window

Visualisation 2 D • VC -> NVC – Maintien des positions relatives

Visualisation 2 D • VC -> NVC – Nous pouvons alors déduire (xv, yv) par

Visualisation 2 D • VC -> NVC – Séquences de transformations correspondantes • Scaling avec comme point de référence (xwmin, ywmin) (fenêtre) • Translation à la position du viewport (xvmin, yvmin)

Transformations géométriques 3 D de base • Translation – La translation d’un point 3 D s’effectue par l’addition des distances de décalage tx, ty et tz aux coordonnées d’origine du point (x, y, z) permettant son déplacement à la position (x’, y’, z’)

Transformations géométriques 3 D de base • Translation – Sous forme matricielle (coordonnées homogènes)

Transformations géométriques 3 D de base • Translation – La translation d’un objet 3 D revient à déplacer les points de l’objet. Pour un objet 3 D représenté par un ensemble de surfaces polygonales, la translation est appliquée sur les sommets. Ensuite, l’objet est retracé

Transformations géométriques 3 D de base • Translation d’un objet 3 D

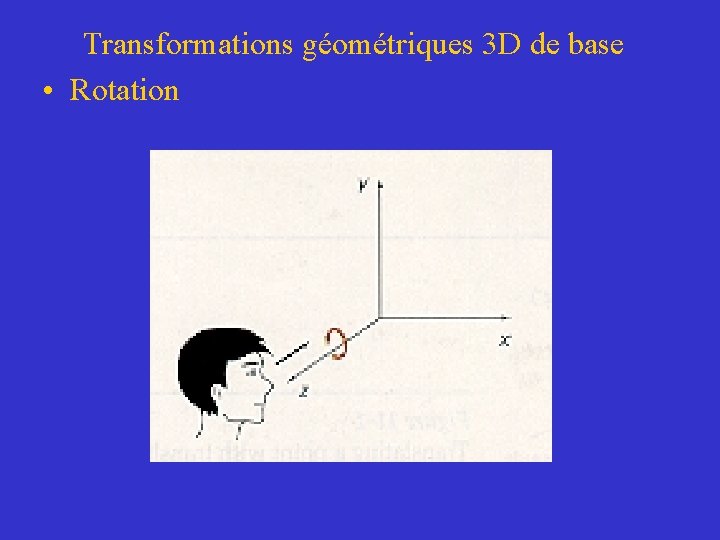
Transformations géométriques 3 D de base • Rotation – Pour faire subir une rotation à un objet 3 D nous devons désigner au préalable un axe et un angle de rotation – Une rotation 3 D peut s’effectuer par rapport à n’importe quel axe dans l’espace – Les rotations les plus simples sont celles par rapport à des axes parallèles aux axes du système de coordonnées – Par convention, un angle de rotation ( ) positif produit une rotation anti-horaire par rapport à un axe de coordonnées

Transformations géométriques 3 D de base • Rotation

Transformations géométriques 3 D de base • Rotation 3 D par rapport à l’axe z

Transformations géométriques 3 D de base • Rotation 3 D par rapport à l’axe z

Transformations géométriques 3 D de base • Rotation 3 D par rapport à l’axe x (x->y->z->x)

Transformations géométriques 3 D de base • Rotation 3 D par rapport à l’axe x

Transformations géométriques 3 D de base • Rotation 3 D par rapport à l’axe y (y->z->x->y)

Transformations géométriques 3 D de base • Rotation 3 D par rapport à l’axe y

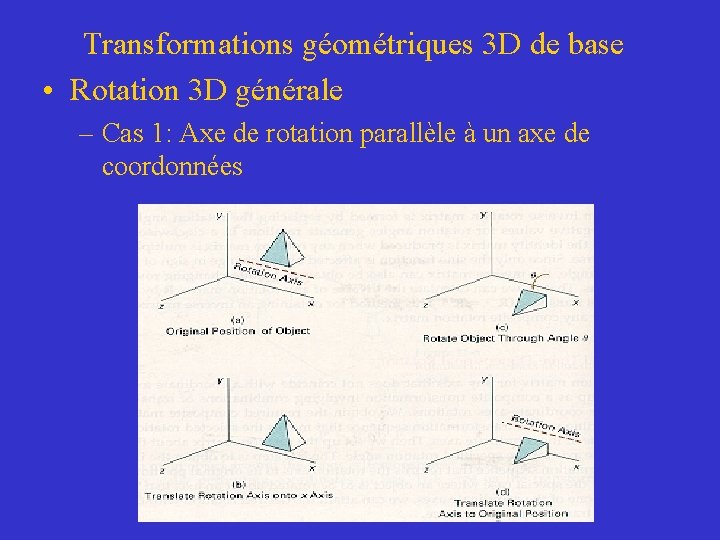
Transformations géométriques 3 D de base • Rotation 3 D générale – Une rotation par rapport à un axe quelconque est représentée par une combinaison de translations et de rotations par rapport aux axes de coordonnées – Cas 1: Axe de rotation parallèle à un axe de coordonnées • Translation de l’objet pour amener l’axe de rotation sur l’axe de coordonnées • Rotation de l’objet par rapport à cet axe de coordonnées • Translation de l’objet pour ramener l’axe de rotation à sa place originale

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 1: Axe de rotation parallèle à un axe de coordonnées

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 1: Axe de rotation parallèle à un axe de coordonnées

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Translation de l’objet pour faire passer l’axe de rotation par l’origine • Rotation de l’objet pour faire coïncider l’axe de rotation avec un des axes de coordonnées (axe z) • Rotation de l’objet par rapport à cet axe de coordonnées • Rotation inverse de l’objet pour ramener son axe de rotation à son orientation originale • Translation inverse de l’objet pour ramener l’axe de rotation à sa place originale

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Un axe de rotation peut être défini par 2 points ou par un point et les cosinus directeurs entre l’axe de rotation et les axes de coordonnées

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Un vecteur axial est donné par

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Un vecteur unitaire dans la direction de l’axe de rotation est donné par

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Étape 1: Translation de l’axe de rotation

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Étape 2: Rotation de l’axe de rotation sur l’axe z – Rotation par rapport à l’axe x pour amener u dans le plan xz – Rotation par rapport à l’axe y pour amener u sur l’axe z

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Étape 2: Rotation de l’axe de rotation sur l’axe z – Rotation par rapport à l’axe x pour amener u dans le plan xz

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Étape 2: Rotation de l’axe de rotation sur l’axe z – Rotation par rapport à l’axe x pour amener u dans le plan xz » L’angle est l’angle entre la projection de u dans le plan yz et l’axe z » La projection de u dans le plan yz est u’ = (0, b, c), cos et sin sont donnés par

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Étape 2: Rotation de l’axe de rotation sur l’axe z – Rotation par rapport à l’axe y pour amener u sur l’axe z

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Étape 3: Rotation de l’objet par rapport l’axe z

Transformations géométriques 3 D de base • Rotation 3 D générale – Cas 2: Axe de rotation non parallèle à un axe de coordonnées • Pour accomplir les étapes 4 et 5 il faut effectuer les transformations inverses Rx-1, Ry-1 et T-1 • La matrice de transformation composée est alors

Transformations géométriques 3 D de base • Changement d’échelle 3 D

Transformations géométriques 3 D de base • Changement d’échelle 3 D

Transformations géométriques 3 D de base • Changement d’échelle 3 D relatif à un point de référence

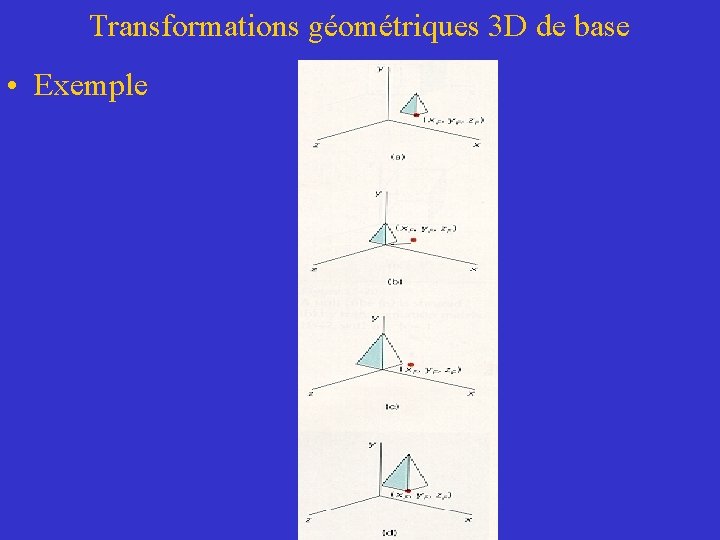
Transformations géométriques 3 D de base • Exemple

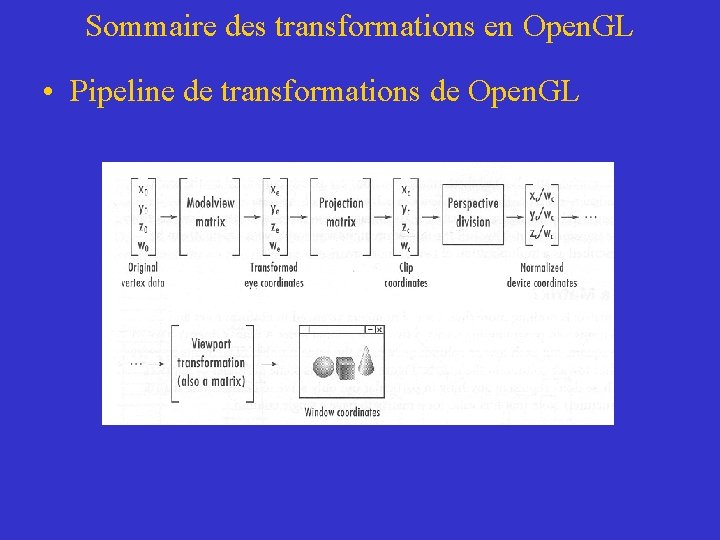
Sommaire des transformations en Open. GL • Pipeline de transformations de Open. GL

Sommaire des transformations en Open. GL • Sommaire des transformations – Visualisation: Permet de spécifier la position de l ’observateur – Modélisation: Permet le déplacement des objets dans la scène – MODELVIEW: Représente la dualité entre les transformations de visualisation et de modélisation – Projection: Permet le découpage et le dimensionnement du volume de visualisation – Viewport: Permet la mise à l ’échelle finale dans le fenêtre d ’affichage

Sommaire des transformations en Open. GL • Transformation MODELVIEW – Les transformations de modélisation et de visualisation son dual l ’un avec l ’autre – Il n ’existe pas de différence entre déplacer un objet vers l ’arrière et déplacer le système de coordonnées de visualisation dans le sens inverse (vers l ’avant) – Il n ’existe pas de différence à faire une rotation sur un objet et appliquer une rotation - sur le système de coordonnées de visualisation – Le terme MODELVIEW indique nous pouvons voir cette transformation comme étant soient de modélisation ou de visualisation

Sommaire des transformations en Open. GL • Matrice MODELVIEW – Matrice de 4 X 4, représente la transformation requise pour transformer les coordonnées du monde en coordonnées de visualisation – Exemple de translation (cube) glut. Wire. Cube(10. 0 f); // dessine un cube de 10 unités // centré par rapport au système de // coordonnées de visualisation gl. Translatef(0. 0, 10. 0 f, 0. 0 f) glut. Wire. Cube(10. 0 f);

Sommaire des transformations en Open. GL • Matrice MODELVIEW – Exemple de rotation (cube) glut. Wire. Cube(10. 0 f); glrotatef(90. 0 f, 1. 0 f) glut. Wire. Cube(10. 0 f);

Sommaire des transformations en Open. GL • Matrice MODELVIEW – Exemple deux translations (cube) glut. Wire. Cube(10. 0 f); gl. Translatef(0. 0, 10. 0 f, 0. 0 f) glut. Wire. Cube(10. 0 f); gl. Translatef(10. 0, 0. 0 f) glut. Wire. Cube(10. 0 f);

Sommaire des transformations en Open. GL • Matrice MODELVIEW – Exemple deux translations par rapport au système de coordonnées de visualisation (cube) glut. Wire. Cube(10. 0 f); gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); gl. Translatef(0. 0, 10. 0 f, 0. 0 f) glut. Wire. Cube(10. 0 f); gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity(); gl. Translatef(10. 0, 0. 0 f) glut. Wire. Cube(10. 0 f);

Sommaire des transformations en Open. GL • Voir l ’exemple ATOM pour l ’utilisation des transformations de base

Sommaire des transformations en Open. GL • Voir l ’exemple ATOM pour l ’utilisation des transformations de base